滚动时域状态估计中极小化问题的求解

胡 磊，伊国兴，南 熠

(哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001)

滚动时域状态估计中极小化问题的求解

胡 磊，伊国兴，南 熠

(哈尔滨工业大学航天学院，黑龙江 哈尔滨 150001)

滚动时域状态估计(MHSE)方法的基本思想是：将控制系统的状态估计问题转化为有限时域内的优化问题，通过获得的优化解对系统状态进行估计。针对带约束的线性离散系统的状态估计问题，介绍了MHSE方法的研究及应用现状。基于惩罚函数法建立惩罚因子，将约束条件融合到适应度函数中，通过粒子群优化(PSO) 算法求解MHSE方法中的极小化问题。基于Matlab编程，实现了二阶仿真算例。仿真结果表明，PSO算法能够有效地求解MHSE方法中的极小化问题，使得2种状态的估计值和真实值之间的均方差分别为0.075 0、 0.204 1。PSO算法能够有效地求解二阶仿真算例，以获取滚动时域估计方法中极小化问题的最优解，为基于MHSE方法进行状态估计的研究与应用提供了参考。下一步的研究方向是提高估计精度，以及复杂约束条件下高阶系统的极小化问题的求解。

状态估计； 适应度函数； 滚动窗口； 约束； 极小化； 粒子群优化算法； 惩罚函数

0 引言

许多控制系统往往需要通过状态反馈对系统进行优化，以达到性能指标要求。然而，并非所有的系统状态变量均易于直接检测，有些状态变量甚至根本无法检测[1]。此外，在实际系统中，外部干扰往往存在约束，例如干扰具有下界或者在某个范围内波动。为了优化上述类型的控制系统，研究带约束的系统状态估计是十分有意义的。

滚动时域状态估计(moving horizon state estimation，MHSE)方法自提出以来，受到了工程界众多学者的关注。MHSE方法对于工业过程的参数估计和状态估计问题，具有良好的效果[2]。该方法将估计问题转化为优化问题，同时又能包含系统的约束条件，利用在线滚动优化原理进行状态估计[3]。文献[4]将MHSE方法应用于具有不确定性的冰山漂移预测。文献[5]将MHSE方法应用于带有未知输入的线性离散系统的状态估计。文献[6]将MHSE方法应用于具有参数不确定系统的状态估计。但以上文献都未具体指出MHSE方法中极小化问题的求解方法。因此，研究其求解方法是十分有意义的。针对上述问题，建立惩罚因子，对具有上下界的状态约束进行处理；采用粒子群优化(particle swarm optimization,PSO)算法对MHSE方法中的极小化问题进行求解，得出系统的初始状态和扰动，实现了对系统状态变量的估计。

1 滚动时域状态估计方法

MHSE方法基于测量输出来估计系统状态。考虑如式(1)所示的线性离散系统。系统满足条件xk∈X、uk∈U、ωk∈W、vk∈V，域W、X、V、U为凸集。

(1)

式中：xk∈Rn为系统状态；uk∈Rg为系统输入；yk∈Rp为测量输出；ωk∈Rm为外部干扰；vk∈Rp为测量噪声。

(2)

式中：j为粒子数。

全信息MHSE方法将线性离散系统(1)的状态估计问题描述为如下所示的数学规划问题1。

问题1[6]：

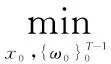
(3)

式(3)满足时域约束条件和动力学方程，分别为：

式中：D为单个粒子的维数。

近似MHSE方法将线性离散系统(1)的状态估计问题描述为如下所示的数学规划问题2。

问题2[6]：

(4)

式(4)满足时域约束条件和动力学方程，分别为：

Πk+1=BQB′+A(Πk-ΠkC′(R+CΠkC′)-1CΠk)A′

2 粒子群优化算法

PSO算法的基本思想是：基于迭代所积累的自身经验以及全局经验，更新粒子的速度和位置，将当代粒子代入适应度函数中求值，并与历史最佳适应度函数值相比较，选取满足目标问题且使之最优的解。PSO算法易于实现、参数较少，能有效解决复杂优化任务[7-9]。因此，针对外部扰动有下界的线性离散系统，在基于MHSE方法实现其状态估计时，选择PSO算法对MHSE方法中的极小化问题进行求解，以期获得包含初始状态和干扰的最优解，进而实现系统的状态估计。

粒子的速度和位置更新公式如下：

式中：t为迭代次数；粒子数j=1,2，…，n，n为整个种群的大小；α1和α2为(0,1)中随机抽取的均匀随机数；η为惯性权重；μ1和μ2为加速度权重系数；Xj=[xj,1,xj,2,…,xj,D]为第j个粒子的位置；vj=[vj,1，vj,2,…,vj,D]为第j个粒子的速度；Sj=[sj,1，sj,2,…,sj,D]为第j个粒子的历史最佳位置。

第(t+1)次迭代时，粒子的历史最佳位置的计算公式如下：

式中：f(·)为适应度函数。

第(t+1)次迭代时，粒子群体历史最佳位置的计算公式如下：

式中：S0=[s0,1,s0,2,…，s0,D]为群体的历史最佳位置。

3 模型建立

针对式(1)所示的线性离散系统，假设输入u(k)=0，测量输出集合为Y=[y0，y1，…，yT-1]T，分别考虑外部干扰没有约束条件以及外部干扰在某个给定范围内波动这一约束条件，建立了无约束条件模型和有约束条件模型。

3.1 无约束条件模型

当T≤N时，定义X=[x0,ω0,ω1,…,ωT-1]T，由式(4)定义如下适应度函数。

推导得：

(5)

当T>N时，定义X=[xT-N，ωT-N，ωT-N+1，…,ωT-1]T，由式(4)定义如下适应度函数。

推导得：

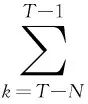
(6)

3.2 有约束条件模型

约束优化问题是科学研究和工程应用中普遍存在的一类优化问题[10]。通常，处理约束优化问题的方法主要有修理法、丢弃法和惩罚函数法等。惩罚函数法将约束优化问题中的违反约束项乘以惩罚项并加到目标函数中，从而构造出带参数的增广目标函数[11]。针对约束条件ωk≥0，惩罚函数法能够更好地处理约束条件，求取优化目标解。

因此，本文选取惩罚函数法对约束进行处理。具体过程是：建立惩罚因子δ，将约束优化问题中的约束条件ωk≥0融合到适应度函数中，进而用粒子群优化方法来求解。构造如下惩罚函数和目标函数。

(7)

F(X,δ)=f(X)+δ×P(X)

(8)

式中：δ为惩罚因子，取正数，大小视实际仿真情况而定；f(X)来自式(5)、式(6)。

以F(X,δ)作为新的适应度函数：当X是目标解时，P(X)=0，F(X,δ)=f(X)；当X不是目标解时，P(X)>0，δP(X)>0，F(X,δ)>f(X)，使得X代入目标函数所得的解不是最小值，需要进一步迭代寻优。

4 估计系统仿真试验

作为验证PSO算法能够求解极小化约束问题的仿真示例，考虑约束条件为ω(k)≥0、输入u(k)=0的线性离散系统为[6]：

(9)

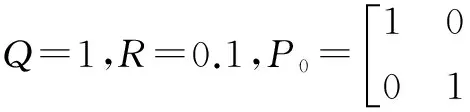
图1 仿真结果(无约束,N=1)

取滚动时域窗口长度N=1，对有约束条件下线性离散系统(9)的状态x1和x2进行仿真，结果如图2所示。图2中，估计值和真实值之间的均方差为σ1=0.091 4、σ2=0.317 4。

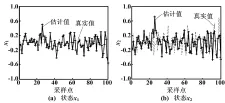
图2 仿真结果(有约束,N=1)

取滚动时域窗口长度N=4，对有约束条件下线性离散系统(9)的状态x1和x2进行仿真，结果如图3所示。图3中，估计值和真实值之间的均方差为σ1=0.075 0、σ2=0.204 1。

图3 仿真结果(有约束,N=4)

从图1～图3及其对应的σi值可以看出，针对二阶线性离散系统(9)，可基于PSO 算法求解MHSE方法中的极小化问题，得出系统的初始状态和干扰，进而求出当前时刻的状态估计。

5 结束语

针对线性离散系统状态估计问题，深入分析了滚动时域估计方法，通过严格的数学推导，得到了适应度函数表达式，并研究了无约束条件的线性离散系统。采用PSO优化算法对适应度函数进行寻优，并研究了有约束条件的线性离散系统。采用惩罚函数法来处理该约束条件，将约束条件融合到增广目标函数中，生成新的适应度函数，并采用PSO优化算法求解。基于Matlab编程,实现了对1个二阶实例的仿真验证。仿真结果表明，PSO算法能够对MHSE方法中的极小化问题进行求解，PSO算法结合惩罚函数法能够对有下界的外部干扰进行处理。

尽管PSO算法实现了对MHSE方法中极小化问题的求解，但是对于如何提高估计精度，以及对复杂约束条件下高阶系统的极小化问题的求解，仍需要进一步探讨和研究。

[1] 王红,吴险峰,张友.离散时间模糊控制系统的新型状态观测器设计[J].数学的实践与认识,2015,45(16):152-158.

[2] ZAVALA V M,BIEGLER L T.Optimization-based strategies for the operation of low-density polyethylene tubular reactors:moving horizon estimation[J].Computers & Chemical Engineering,2009:33(1):379-390.

[3] ANGELO A,MAURO G.Moving-horizon estimation for discrete-time linear and nonlinear systems using the gradient and Newton methods[C]//Conference on Decision and Control(CDC).Las Vegas:IEEE,2016:2906-2911.

[4] LEIFERIK A,FRANCESCO S,LARS I.The moving horizon estimator used in iceberg drift estimation and forecast[C]//European Control Conference(ECC).Denmark:IEEE,2016:1271-1277.

[5] BOULKROUNE B,DAROUACH D,ZASADZINSK M.Moving horizon estimation for discrete time linear systems with unknown inputs[C]//Proceedings of the European Control Conference 2007.Greece:IEEE,2007:2875-2878.

[6] 赵海燕.时域约束系统的滚动时域状态估计方法研究[D].长春:吉林大学,2007:14-21.

[7] 王东,风孟丽,赵文杰.基于自适应搜索中心的骨干粒子群算法[J].计算机学报,2016,39(12):2652-2667.

[8] 邓丽,蒋婧,费敏锐.基于免疫粒子群算法的PID参数整定与自适应[J].自动化仪表,2013,34(2):65-67.

[9] 杨琳,孔峰.嵌入粒子群优化算法的混合人工蜂群算法[J].自动化仪表,2013,34(1):50-53.

[10]刘云连,伍铁斌,王俊年,等.改进罚函数法与蝙蝠算法在约束优化中的应用[J].计算机工程与应用,2015,9(9):62-67.

[11]蔡海鸾.惩罚函数法在约束最优化问题中的研究与应用[D].上海:华东师范大学,2015:5-6.

SolutionoftheMinimizationinMovingHorizonStateEstimation

HU Lei,YI Guoxing,NAN Yi

(School of Astronautics,Harbin Institute of Technology,Harbin 150001，China)

The basic idea of moving horizon state estimation(MHSE) method is to convert the state estimation of the control system into the optimization in the finite time domain,and obtain the optimal solution to implement estimation of system state.In order to solve the state estimation of linear discrete systems with constraints,the research and current status of application of MHSE method are presented.The penalty factor is established based on the penalty function method,the constraint condition is integrated into the fitness function,and the minimization in the MHSE method is solved by the particle swarm optimization(PSO) algorithm.On the basis of Matlab programming,the second order simulation case is realized. The simulation results show that the PSO algorithm can effectively solve the minimization in the MHSE method,so that the mean square error between the estimated value and the true value of the state andis 0.075 0 and 0.204 1.The PSO algorithm can effectively solve the second-order simulation case,to obtain the optimal solution of the minimization in the moving horizon state estimation method,which provides reference for the research and application of state estimation based on MHSE method.The next step is to improve the estimation accuracy and solve the minimization of the high order system with complex constraints.

State estimation; Fitness function; Moving window; Constraint; Minimization; PSO algorithm; Penalty function

修改稿收到日期:2017-07-26

胡磊(1993—)，男，在读硕士研究生，主要从事智能算法的研究，E-mail：maple_hsjz@163.com；伊国兴(通信作者)，男，博士，教授，主要从事先进导航与无人机智能控制等方向的研究,E-mail：ygx@hit.edu.cn

TH-3；TP13

A

10.16086/j.cnki.issn1000-0380.201712011