三电平结构SVG输出电流谐波分析及滤波器设计*

李元正，陈劲操，马炳洲，孙瑜

（南京理工大学 能源与动力工程学院，南京 210094）

0 引 言

静止无功发生器（SVG）通过控制逆变器中电力电子器件进行工作，因此其输出会不可避免的含有谐波成分，而大量谐波进入电网会导致电网电压、电流波形发生畸变，影响电网的稳定运行。因此，必须对SVG装置网侧接入滤波器后才能使其接入电网。

目前，对SVG的研究主要集中在主电路拓扑结构和控制算法方面［1-4］。文献［5］提出装置中选择滤波器方法，并没有提出相应的设计方法。文献［6-9］在仿真数据的基础上总结出多电平PWM波形的谐波特点并提出了输出滤波器设计方法，但其仅仅依靠仿真分析说明，缺乏足够的理论推导，而且逆变器输出滤波器设计方法并不适合直接用于SVG输出滤波器设计。文献［10-11］分别就整流器和有源电力滤波器装置（APF）输出进行分析讨论并提出滤波器设计方案，并不能完全指导无功补偿装置的输出滤波器设计。文献［12］对二电平静止无功发生器LCL和L输出滤波器进行分析比较并提出设计方案，但三电平结构与二电平结构输出电流波形有较大差异，因此需要对三电平逆变器结构特点以及输出谐波分析并提出适合三电平静止无功发生装置输出滤波器设计方案。

为此，文章通过研究三电平SVG主电路结构、调制方法，利用双傅里叶变换分别对二电平和三电平逆变器输出电流进行分析并且计算得到两种逆变器的输出电流纹波，为滤波器设计提供了理论依据。

1 三电平静止无功发生器结构与输出电流分析

采用LCL滤波器的三电平SVG装置结构如图1所示。

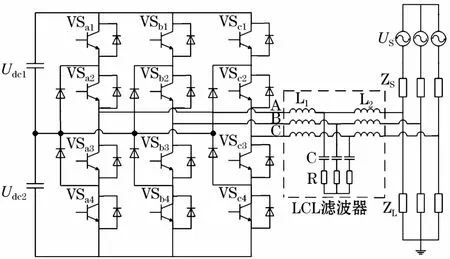
图1 采用LCL滤波器的SVG装置结构图Fig.1 Structure diagram of SVG device adopting LCL filter

Udc1、Udc2为SVG逆变器直流侧电压，VSk为k相开关管，US为电网电压，ZS为线路阻抗，ZL为负载阻抗，L1、L2、C和R共同组成了LCL滤波器。以下论文中，SVG输出电流为L2流入电网电流，电网电流为流经ZS电流，负载电流为流经ZL电流。

SVG通过PWM控制技术输出近似正弦波的电流，但会产生与开关频率有关的谐波分量与电流纹波。因此，在设计滤波器过程中要先对逆变器输出电流谐波含量以及电流纹波的特点进行分析。不同的调制方法以及主电路拓扑结构输出电流特点不同，本文为简化分析，对基于SPWM调制方法的三电平二极管箝位式拓扑结构以及传统二电平拓扑结构输出电流波形进行对比分析。

1.1 电流谐波分量分析

文献［13］对二电平单相逆变器输出电压进行了较为详细的分析，其使用双重傅里叶变换通过计算得出在二电平状态下a相开关函数：

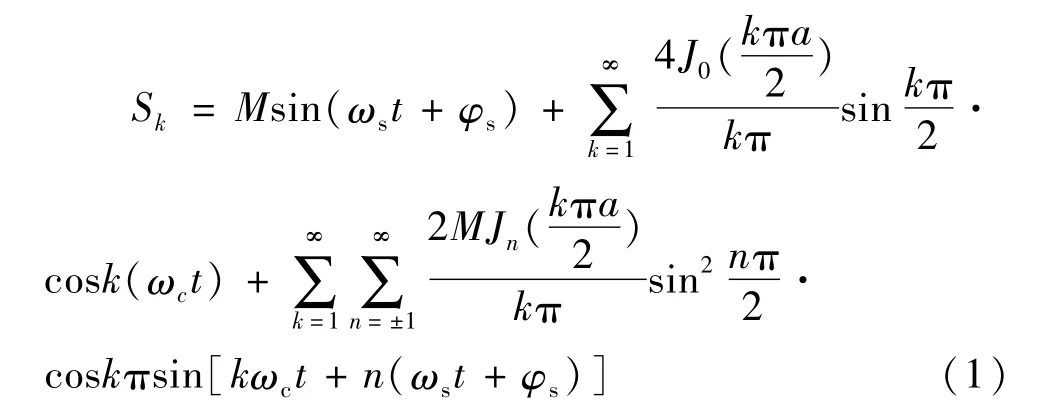
式中Jn为n阶贝塞尔函数，有：

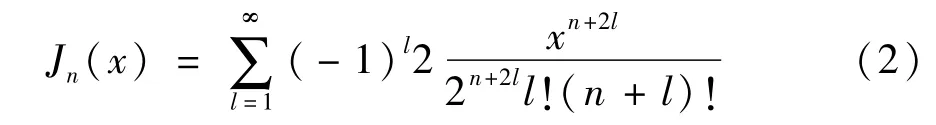
下面对三电平结构SVG的输出电流表达式进行推导。分析三电平SVG输出电流，先对逆变器单相开关状态进行分析。由图1所示二极管箝位式三电平SVG的主电路拓扑：定义VSk为k相开关管，Sk（k=a，b，c）三电平单桥臂开关函数如下：

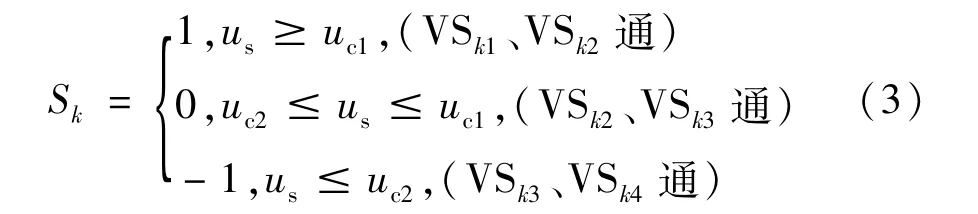
二极管箝位式三电平逆变器a相四个开关管一个周期内输出状态如图2所示。

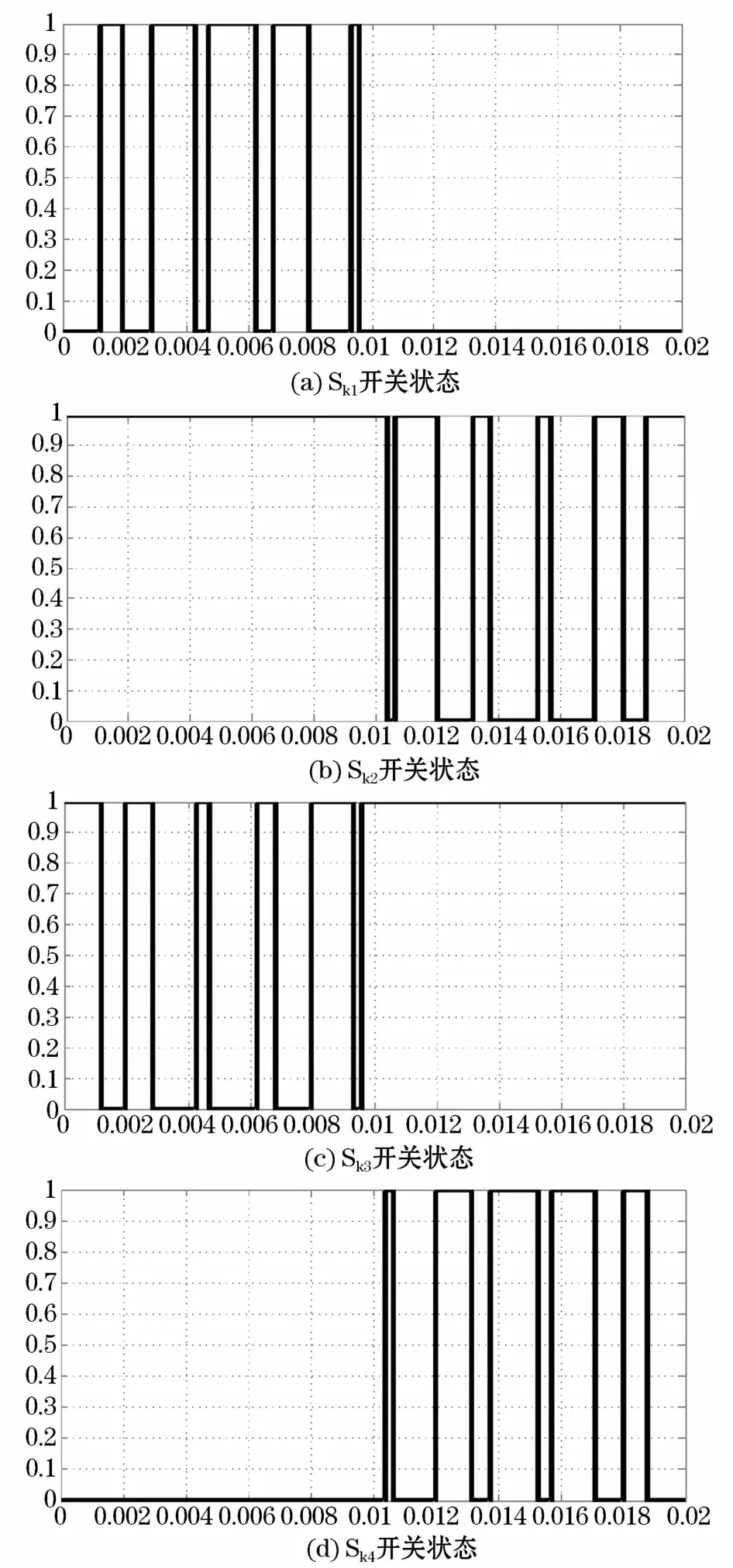
图2 逆变器a相开关状态Fig.2 A-phase switch state of inverter

结合式（10）与图2对三电平单相开关状态进行分析，可将单相开关管状态其等效为单极性SPWM分析，原理图如图3所示。

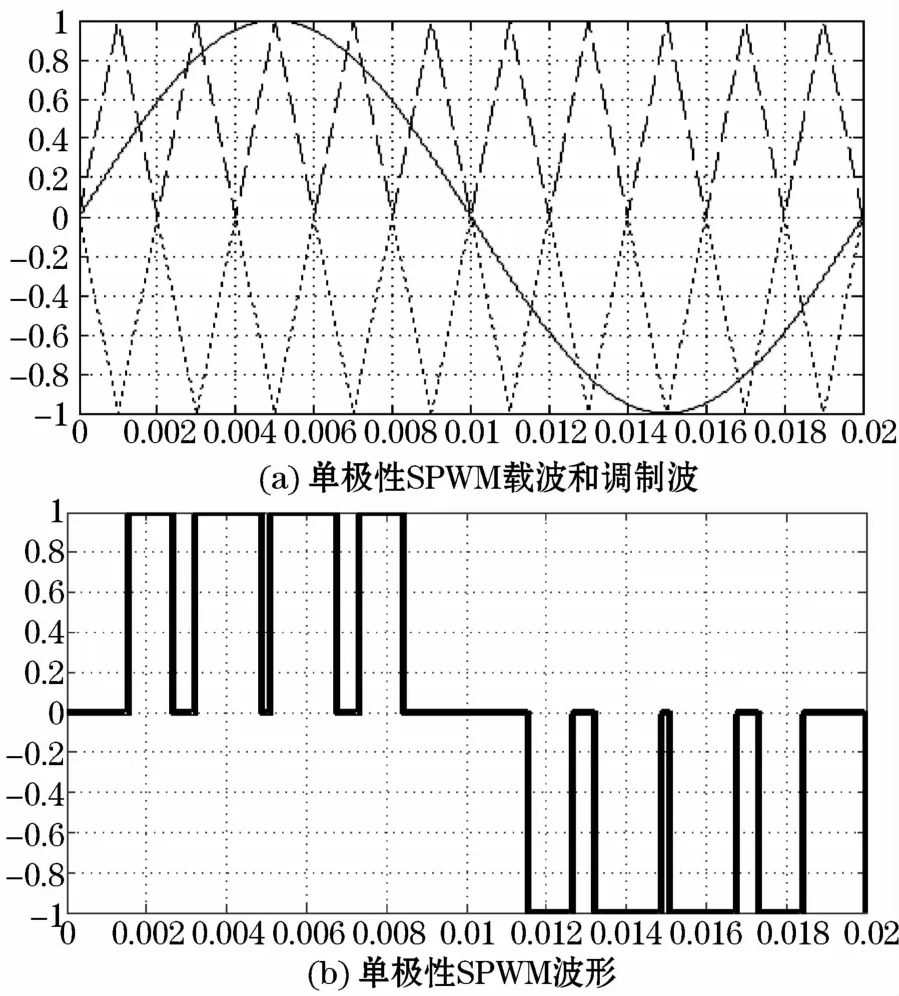
图3 单极性SPWM调制原理Fig.3 Single polarity SPWM modulation principle

对开关管状态进行分析，调制波和载波的数学表达式分别为：

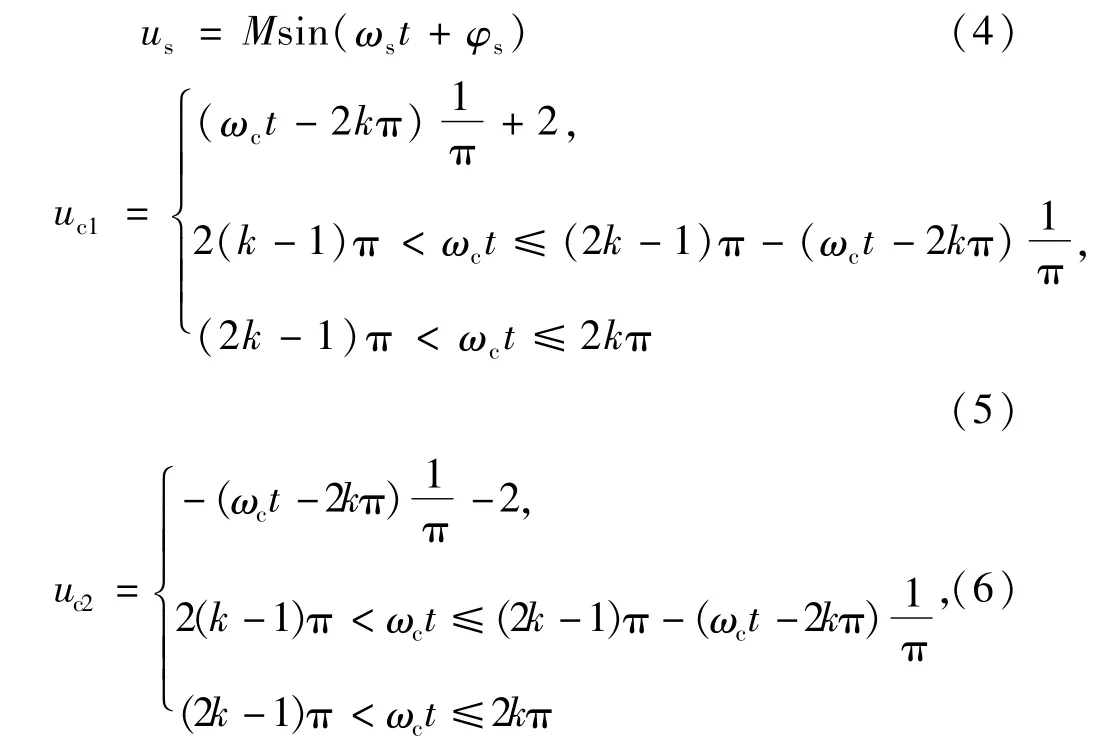
Us为调制波波形，uc1和uc2分别为正半轴载波和负半轴载波，ωs、ωc分别为调制波与载波角速度，M为调制比，联立式（3）～式（6）可以得到单相开关状态表达式：

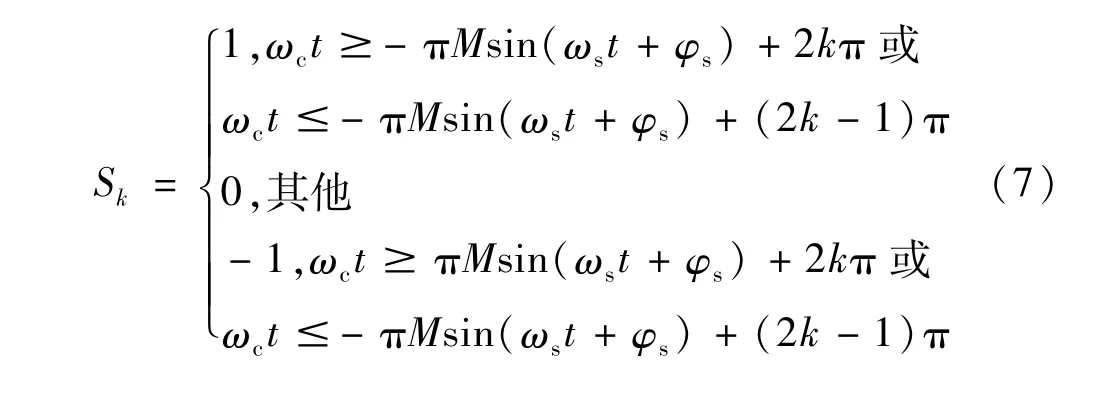
对于以上二元函数可以使用式（8）所示双重傅里叶变换形式分解。

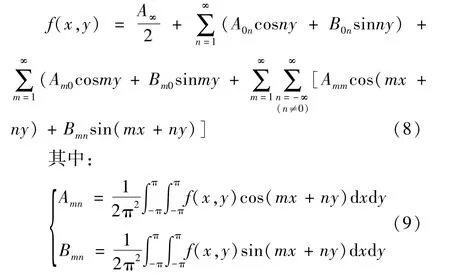
令x=ωc t，y=ωs t+φs，带入式（7）～式（9）整理可以得到三电平单相开关管状态模型：

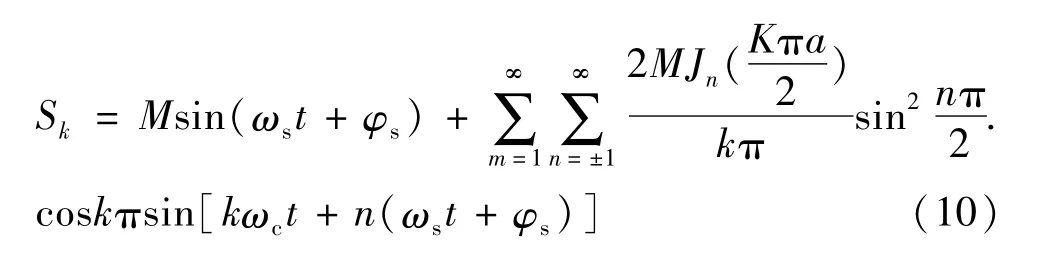
由三相调制波相位差可以分别得到三相桥臂开关管状态，对a相进行分析，a相输出电压为：

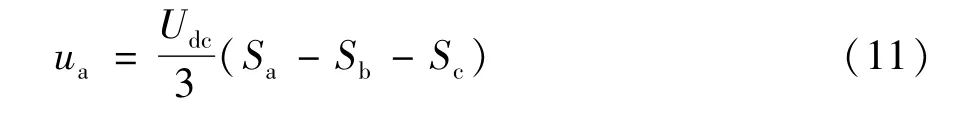
对比式（1）和式（10）可以分析得到，二电平结构与三电平结构SVG单相开关管状态表达式相比，多出式（1）的第二项，可以得到三电平谐波含量较二电平有明显改善。

1.2 输出电流纹波表达式推导

对逆变器侧电流纹波产生滤波作用主要依靠L1［1］，因此，在分析逆变器侧电流纹波时，可将 LCL滤波器等效为L滤波器分析。以a相正半轴为例分析，纹波电流最大值位于正弦波峰值处［8］，VSk1开通时间为TON，关断时间为TOFF，开关周期为TS，占空比为D，Um为输出电压最高值，Udc为直流侧总电压，一个开关周期内电压波形如图4所示。

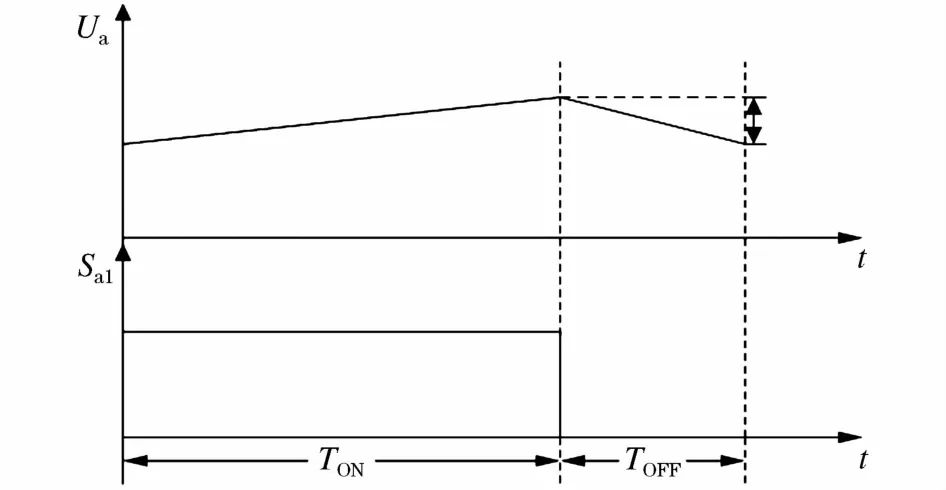
图4 A相单开关周期电压波形Fig.4 Voltagewaveform of A-phase single switch cycle

在0＜t＜TON时，得到：

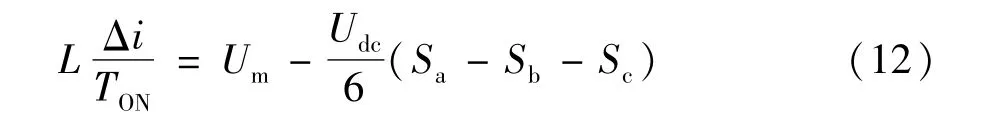
在TON＜t＜TS时，得到：

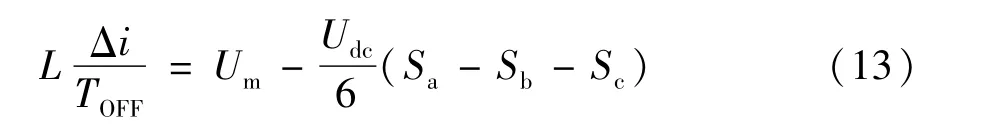
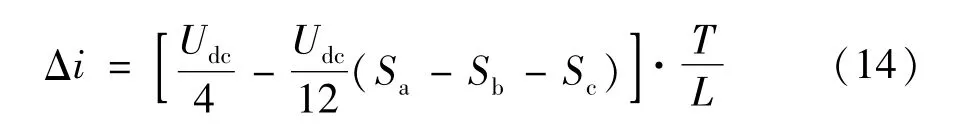
由纹波电流最大值位于正弦波峰值处，取Sb=Sc=-1，推导出最大电流纹波如式（15）所示。为滤波器设计提供了依据。

1.3 输出电流仿真分析

分别对二电平和三电平SVG进行仿真，逆变器结构以及电网设置参数相同，开关频率5 kHz，不安装输出滤波器且负载为阻性时得到输出电流波形以及电流频谱如图5所示。

根据图5分析，谐波分量主要分布在nfS（n=1，2…）的周围，fS为开关频率，这种现象同时适用于二电平和三电平，符合之前理论分析结论。因此，为滤除开关频率附近的高次谐波，设计滤波器应为低通滤波器且截止频率远小于开关频率［14］。

对比二电平和三电平输出电流的总谐波失真率（THD），二电平时THD=91.56%，三电平时THD=42.47%，可以发现三电平SVG输出电流谐波含量明显小于二电平状态，以上仿真结论符合计算结果。

2 LCL滤波器原理分析与设计

2.1 LCL滤波器原理分析

LCL输出滤波器基本原理是在传统L滤波器滤除开关管纹波的基础上接入一个LC滤波器对电流i1中包含的高频谐波进行分流，电容C为高频成分提供低阻通路，从而减少输出电流i2中的高频谐波含量，在电容分路加入阻尼电阻R有利于抑制位于谐振点附近的谐波。由于只考虑输出波形中的高频成分，将电网电压假设为理想电压源不含有谐波，因此US可当做短路分析，单相等效等效电路如图6所示。

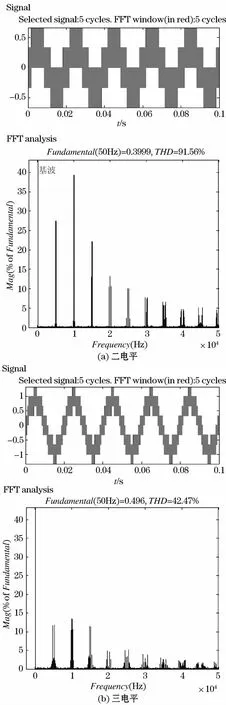
图5 二电平和三电平SVG输出电流仿真波形及FFT分析Fig.5 Simulation waveform of two-level and hree-level SVG output current and FFT analysis

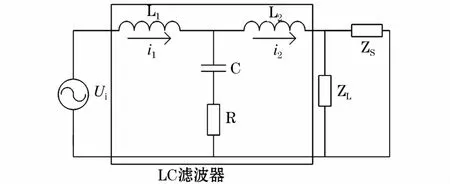
图6 LCL输出滤波器单相等效结构图Fig.6 Single phase equivalent structure diagram of LCL output filter

忽略线路阻抗，通过图6可以分别建立逆变器侧电流i1和网侧电流i2对逆变器输出电压ui的传递函数：

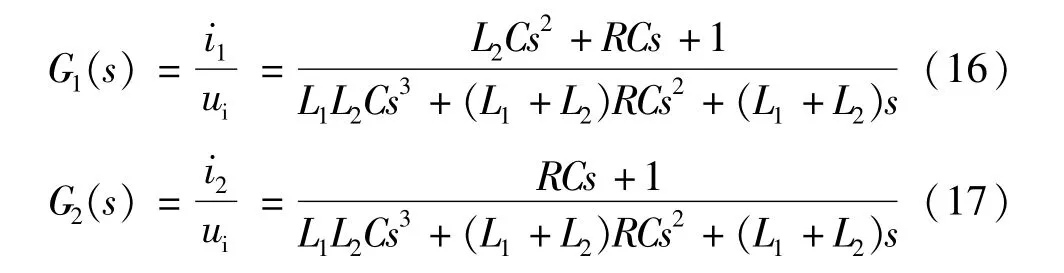
对式（16）～式（17）传递函数进行分析可以得到，在高频段LCL滤波器对逆变器侧谐波滤波效果与L1取值有关［15］，低频段起主要滤波作用的是滤波器电感，即在低频段中当滤波器电感值相同时，传统L滤波器与LC滤波器滤波效果基本相同，LC滤波器中的电容支路主要对高频谐波起滤除作用，总电感值越大滤波效果越好，但是，如果电感值设计过大会导致滤波器两端有较大的压降，影响无功补偿能力。在电容支路接入的电阻越大对谐振抑制作用越明显，但会造成高频段的滤波效果下降。

2.2 LCL滤波器设计

SVG滤波器设计需要根据滤波器特性、系统无功补偿能力、滤波要求、成本及损耗等多方面要求进行设计。

2.2.1 电感参数设计

总电感量主要对于低频段纹波产生作用，总电感量越大，抑制谐波效果越好，但是过大的电感会增加电感两侧压降，影响补偿能力，但如果总电感值太小则会导致滤波器抑制电流纹波能力下降。因此，为了同时取得较好的无功补偿以及谐波抑制效果，需要兼顾这两点。

通常从电感压降方面考虑电感设计最大值，一般要求电感上基波压降不超过电网线电压有效值的10%［16］，即：

而两电平情况下由于电平数量较少，为达到设计要求需要的最小电感Lmin也较三电平要大，因此，在三电平设计下，输出电感值也可以相应下降，由以上分析可知，三电平状态下输出滤波器最小电感量仅相当于二电平状态下的2/3。通常规定最大纹波电流为额定电流的15%～25%，通过上述计算，在三电平情况下，最大纹波电流如式（20）所示，其中η=15%～25%。

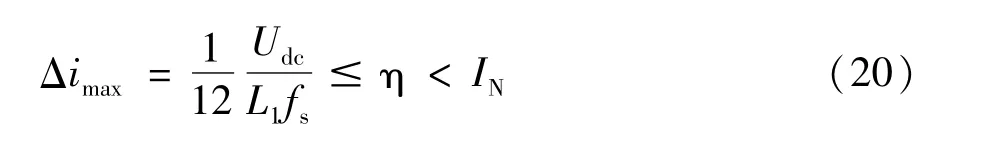
由式（20）可得电感L1的取值范围为：

式中ω为基波角频率；IN为SVG额定输出电流；UL为电网线电压有效值。

根据滤波器的滤波能力要求，L还要根据最大纹波电流设计，在传统两电平情况下，最大纹波电流如式（19）所示［17］，Δimax为最大纹波电流，fs为开关频率。

由文献［1］可知，L1=L2时滤波效果最好，因此，电感取值为：

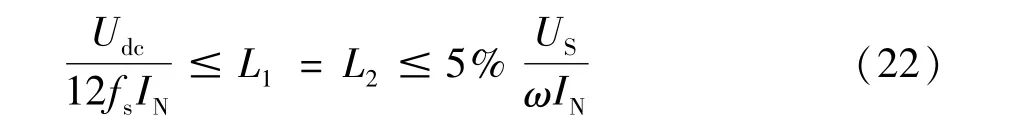
由于实际应用中，线路以及负载都存在感性阻抗，因此实际设计中可以适当减少L2电感量。

2.2.2 滤波电容与阻尼电阻参数设计

由于LCL滤波器属于三阶滤波器，存在谐振频率，在谐振频率下相当于逆变器与电网之间短路，将导致与谐振频率相近的高频谐波大量进入电网。因此，在电容支路串联阻尼电阻降低谐振的同时应在设计时避免谐振点与谐波源频率相近。滤波器谐波频率为通过上述分析，设置滤波频率在20倍基频到0.5倍开关频率之间［4］，如下：

式中fN表示输出电流基波频率，fs表示开关频率。

阻尼电阻的加入可以有效抑制谐振谐振幅值，但是过大的电阻值将影响高频段滤波效果，且会导致电阻发热的状况，通常阻尼电阻设置为谐振点容抗的 1/3［18］，公式如式（24）所示：

3 仿真与实验

为验证三电平净值无功补偿装置输出LC滤波器设计的可行性，在Matlab/Simulink软件中分别建立二电平和三电平SVG系统模型，仿真参数见表1。

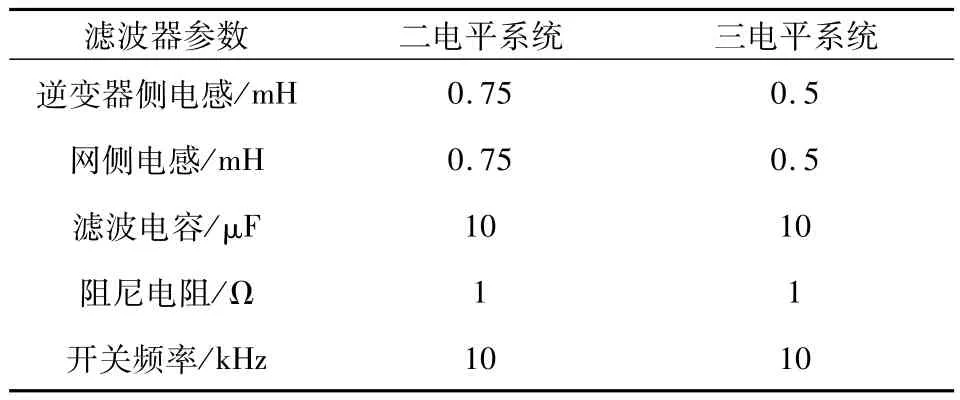
表1 系统仿真参数Tab.1 System simulation parameter

为使仿真负载电流包含谐波分量，负载由阻感性负载以及非线性元件二极管组成，装置投切前负载电流THD=2.42%，FFT分析如图7所示。

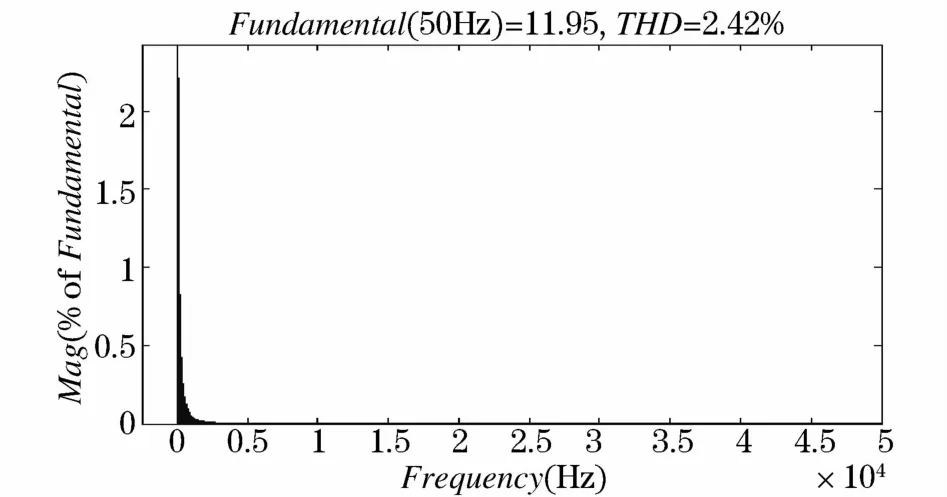
图7 仿真电网负载电流仿真波形FFT分析Fig.7 Load current simulation waveform of power grid and FFT analysis

二电平与三电平SVG系统投切电网补偿仿真波形与投切后电流FFT分析如图8所示，装置在0.05 s投入使用，A线为电压，B线为电流，可以看到装置从补偿效果以及滤波效果方面符合设计要求。

根据图8（b）与图8（d）可知，电网电流在两种系统投放时THD分别为3.05%与3.12%，在电感量明显少于两电平结构情况下，可以取得相似的滤波效果。

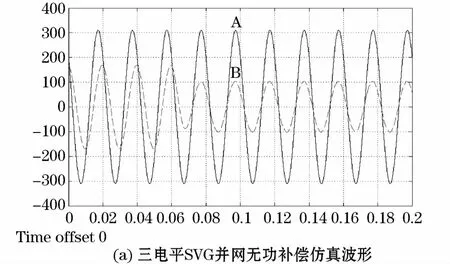
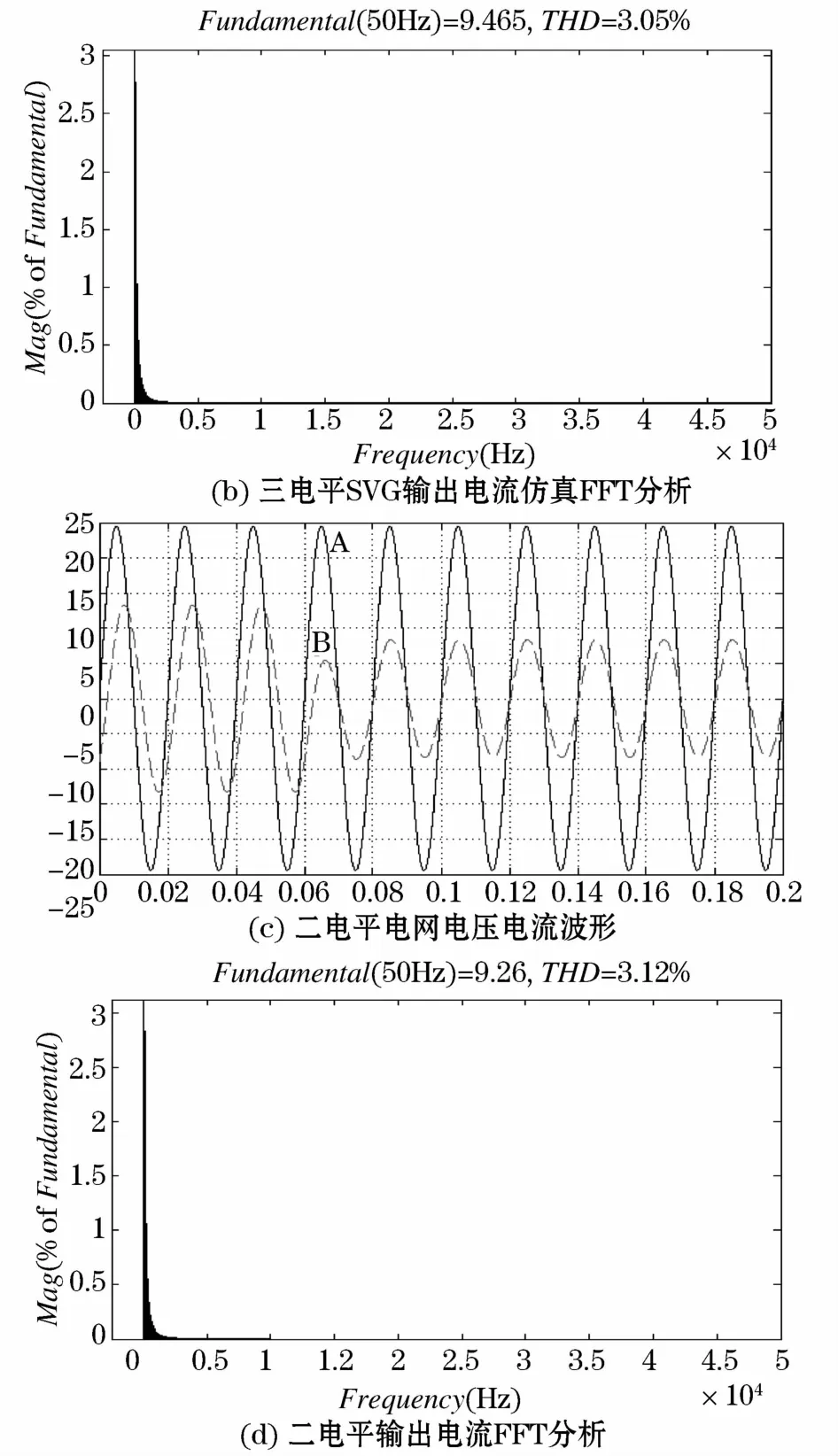
图8 二电平与三电平系统投放电网单相电压电流仿真波形及FFT分析Fig.8 Single phase voltage current simulation waveform of two-level and three-level system and FFT analysis

为进一步论证设计方案的可行性，研制了一台主电路为二极管箝位式三电平逆变器结构的SVG装置，并搭建了相应的实验平台。逆变器输出波形如图9所示。

使用装置投切电网进行实验，使用滤波器逆变器侧电感为0.5 mH，电容为10μF，网侧电感使用线路等效电感代替，开关频率为10 kHz，轻载实验结果如图10所示，三相线路无功功率约为36.2 var，图中曲线A为电压值，曲线 B为电流值，如图10（a）所示，电网存在明显的感性负载，经过检测功率因数为0.760，装备投切后电网电压电流波形如图10（b）所示，功率因数为0.967，无功功率得到较好的补偿。

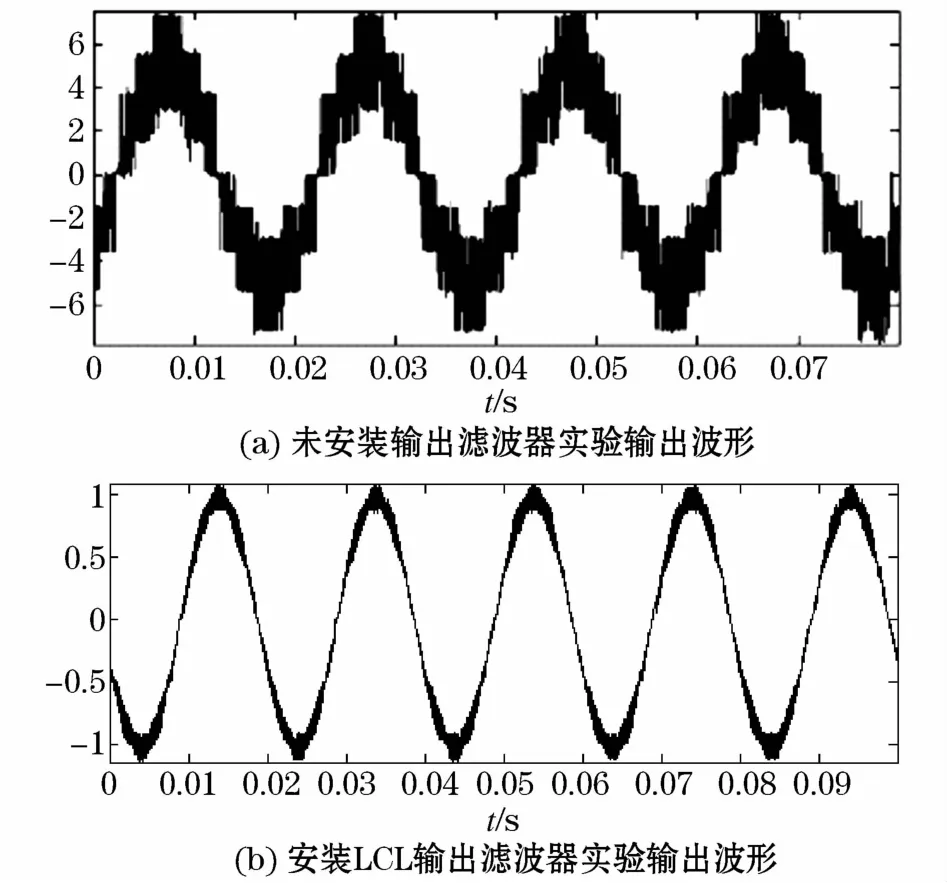
图9 逆变器输出波形Fig.9 Output waveform of inverter

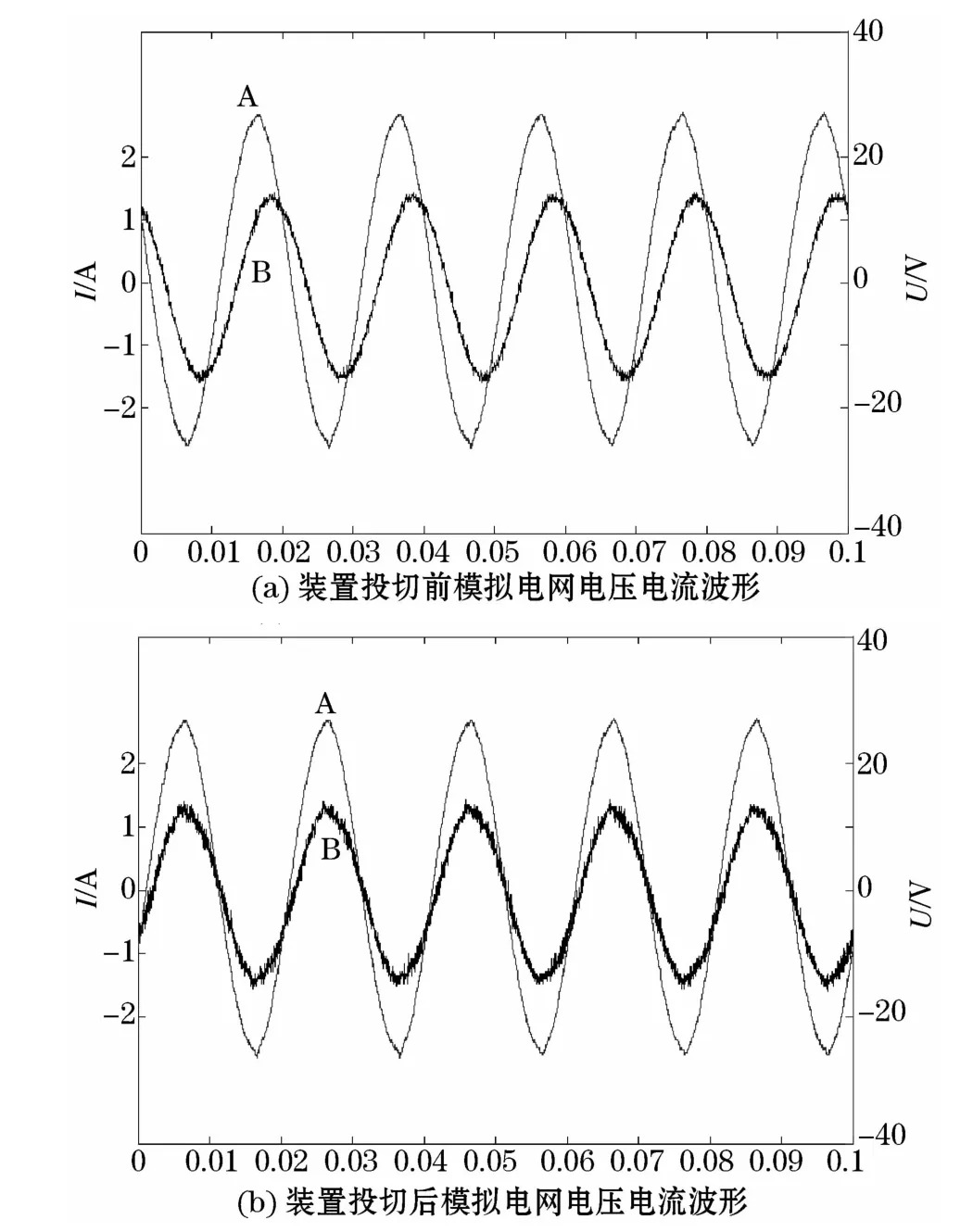
图10 装置投切前后模拟电网的电压电流波形Fig.10 Voltage current waveform of simulated power grid before and after improving the load device switch

装置投切前后电网电流FFT分析结果如图11所示，SVG投切前后总谐波失真分别为4.62%和4.93%，通过图11可以看到，开关频率附近谐波有较好的滤除作用，且增加谐波含量较少。

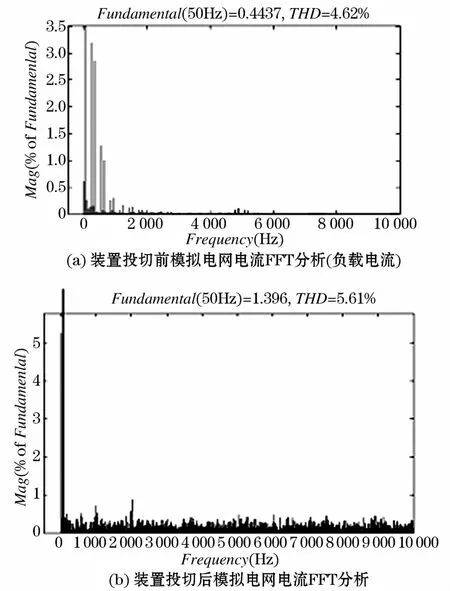
图11 电网轻载装置投切后电网电流FFT分析Fig.11 Power grid current FFT analysis after the switch of grid light load device

进一步提高负载无功功率实验结果如图12所示，图中曲线A为电压值，曲线B为电流值，图12（a）所示为SVG投切前模拟电网电压电流波形，电网存在明显的感性负载，经过检测可知三相线路无功功率约为321 var，功率因数为0.768，装备投切后电网电压电流波形如图12（b）所示，功率因数为0.978，无功功率得到较好的补偿。

装置投切前后电网电流FFT分析结果如图13所示，SVG投切系统前电网电流总谐波失真分别为2.42%与仿真相同，装置投切后电流总谐波失真为3.23%，接近仿真结果，电网谐波含量符合要求。

仿真和实验验证了上述三电平静止无功发生器输出滤波器设计方法的可行性，结果证明，上述设计方法在减小电感数值的同时可以有效的减少SVG装置对电网的谐波污染，减少总电感量可以有效的解决过大电抗器参数取值导致系统容量降低，系统跟踪速度慢［7］等问题，又能解决大电感体积过大、成本过高问题。

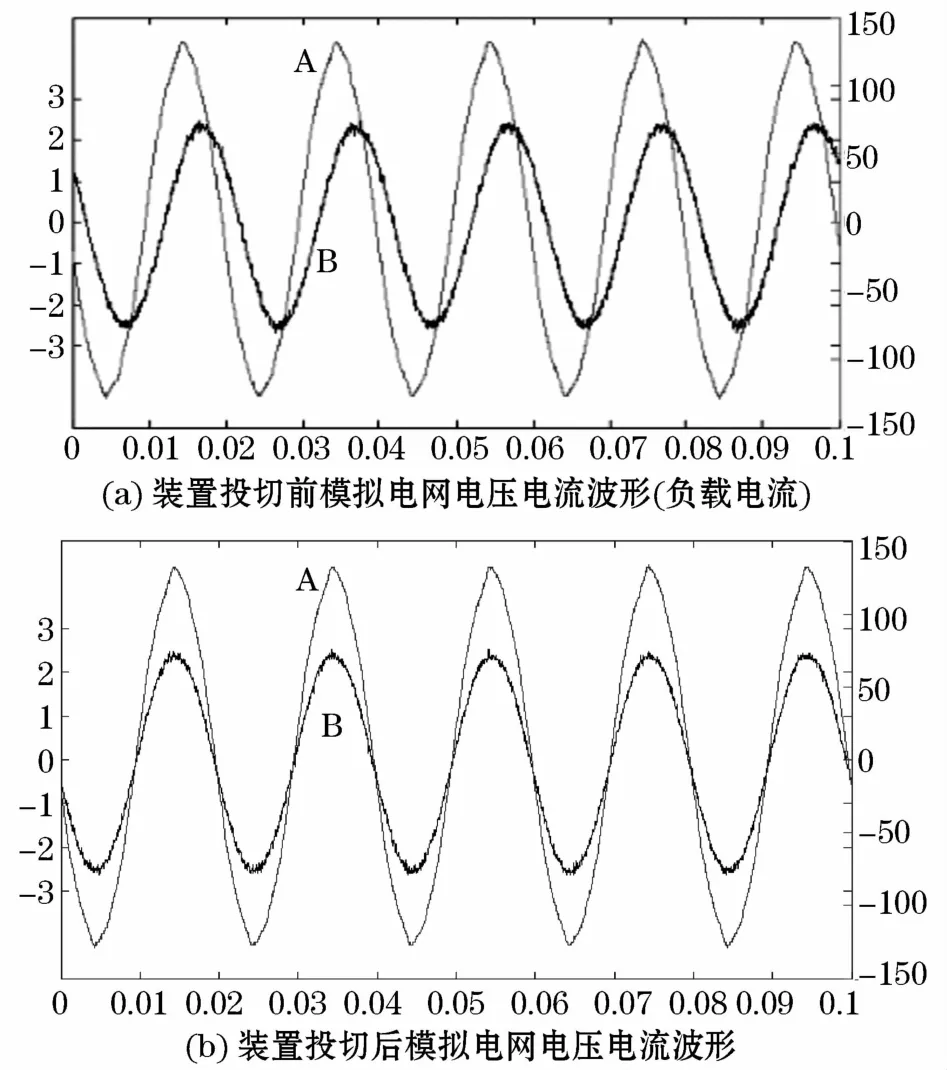
图12 提高负载装置投切前后模拟电网的电压电流波形Fig.12 Voltage current waveform of simulated power grid before and after improving the load device switch

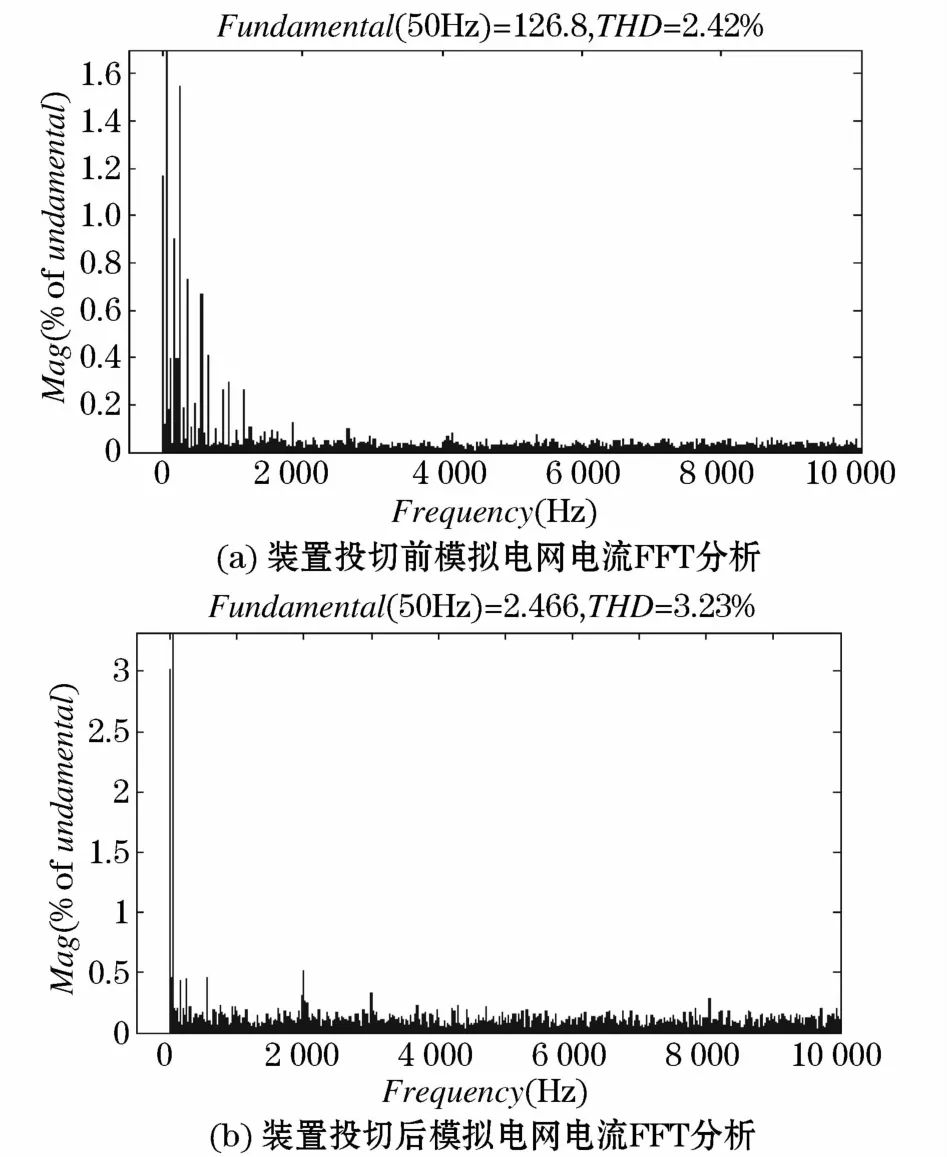
图13 装置投切前后模拟电网的电压电流FFT分析Fig.13 Power grid current FFT analysis before and after device switch

5 结束语

深入分析三电平与二电平SVG输出电流谐波特点与滤波器各元件对滤波效果的影响，推导得到了三电平SVG输出电流表达式以及输出电流纹波表达式。通过对两种逆变器电流纹波的计算，可以知道在达到相同电流纹波要求的情况下，三电平SVG输出滤波器逆变器侧电感值仅需要二电平时的2/3，证明在三电平结构下SVG输出滤波器电感值可小于两电平结构。根据装置无功补偿能力和谐波抑制要求以及三电平SVG输出电流特点设计输出滤波器各部分参数，以此为根据在相关设计原则的基础上提出一种三电平静止无功发生器输出LCL滤波器的设计方法。使其在满足无功补偿能力的前提下，采用较小的电感实现较好的滤波效果。通过仿真和实验，验证了本文提出的三电平SVG滤波器设计方案在降低滤波器电感值的同时可以有效的保证滤波效果，减少SVG装置对电网的污染，提高电能质量。