类方形蜂窝夹芯结构力学性能研究
童 冠,李 响,梅月媛,周幼辉
(1. 福建省送变电工程有限公司,福建福州 350013;2.三峡大学水电机械设备设计与维护湖北省重点实验室,湖北宜昌 443002;3. 三峡大学机械与动力学院,湖北宜昌 443002)
类方形蜂窝夹芯结构力学性能研究
童 冠1,李 响2,3,梅月媛3,周幼辉3
(1. 福建省送变电工程有限公司,福建福州 350013;2.三峡大学水电机械设备设计与维护湖北省重点实验室,湖北宜昌 443002;3. 三峡大学机械与动力学院,湖北宜昌 443002)
为了证明类方形蜂窝结构与六边形蜂窝结构之间的关系,将类方形蜂窝夹芯结构分解为特有的T字形胞元,应用Euler梁原理和能量法分别推导了T字形胞元模型的等效弹性常数公式。同时,在用经典方法推导的六边形蜂窝夹芯的等效弹性常数公式中,代入了类方形蜂窝结构的特征参数,得到了与前述2种方法相同的结果,证明了类方形蜂窝是六边形蜂窝的演变体,指出了这2个经典蜂窝公式存在的局限性和应用范围,由类方形蜂窝的结构特征,发现经典蜂窝理论公式在特征角等于零或零附近的值是奇异和不准确的。研究结果对蜂窝结构力学性能相关理论的后续研究和完善有着重要的参考价值。
结构力学;夹层结构;类方形蜂窝;能量法;等效弹性常数;力学性能
夹层结构是由2块高强度的薄表层板和填充在中间的夹芯层组成的,中间使用新型黏结剂黏结而成[1-2]。表层一般采用金属、玻璃钢、高硬度轻质材料等,而夹芯一般是用泡沫塑料、铝或不锈钢波片、波纹金属钢等制成的蜂窝,其中以铝质正六边形蜂窝的应用最为常见。近年来出现了很多新的蜂窝结构型式,进一步扩大了蜂窝的结构体系和应用范围[3-9]。
研究夹芯面内力学性能的代表人物主要有GIBSON[10-12],BURTON[13]和富明慧[14-15]等,他们采用简化的线弹性Bemoulli-Euler梁模型,推导了蜂窝结构的多个等效弹性参数的解析式,在此基础上展开后续的研究工作,增加考虑弯曲变形、伸缩变形和剪切变形对面内等效刚度的影响,不断对GIBSON公式进行修正。这其中,WARREN等[16]发现胞元周期性重复排列是蜂窝结构的重要特点,于是选取其中代表性的简化胞元进行了分析,创立了此类结构研究方法的一个新范式。
到目前为止,国内外有关蜂窝结构的等效弹性模量参数研究工作大部分都是在胞元理论基础上展开的。本文分别运用Euler梁原理、能量法和经典蜂窝理论,针对类方形蜂窝结构进行深入研究。研究中涉及的主要符号说明见表1。

表1 主要符号说明
1 基于T模型求解等效力学常数
类方形蜂窝结构如图1所示,其由许多正方形的蜂窝孔组成。使用胞元分解原理[16],根据类方形蜂窝胞元周期性重复排列的特点,选取T型胞元模型进行力学分析,见图2。


等效力学参数求解采用等效模型与胞元模型相等的原理。首先,使蜂窝胞元模型处于单向受力状态,推导对应于该状态的应力应变量;然后建立等效模型,将蜂窝夹芯层等效为均质实心体,保持受力状态不变,进行应力应变量求解。由于等效模型结构与原胞元模型结构等价,因而在同样受力状态下2种模型的应力应变量相等,由此建立方程求解,得到夹芯结构的等效力学性能参数。表征蜂窝夹芯结构整体力学性能的3个等效力学性能参数分别是蜂窝夹芯结构面内等效弹性模量Ecx,Ecy和面内剪切模量Gcxy。
如图2所示,虚线所包围的四边形即为类方形蜂窝夹芯胞元,本文称之为“T模型”,其几何要素分别为胞元长h、宽l、壁厚t。T型胞元结构有如下特点:1)T型的长宽所在矩形面积等于类方形蜂窝孔的面积;2)每个T型单元有3个完整胞壁,而单独属于每个类方形蜂窝的完整胞壁也是3个。

1.1 类方形蜂窝x方向等效弹性模量
T型胞元在x方向上的受力图如图3所示,其等效体为虚线所围成的矩形,取厚度t=b的类方形蜂窝胞元进行研究。

1.2 类方形蜂窝y方向等效弹性模量
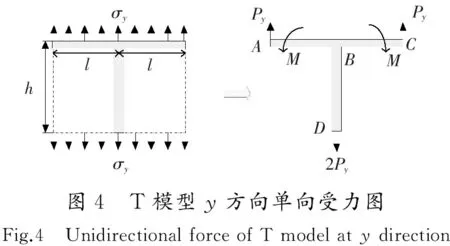
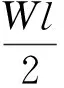
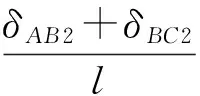

所以,等效泊松比μ2=0 ,等效体在y方向的等效弹性模量为
1.3 类方形蜂窝等效剪切模量
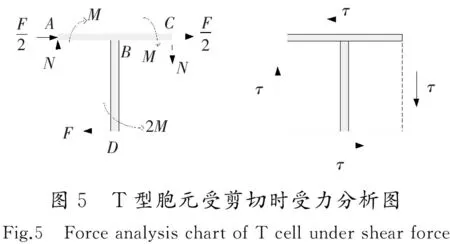
根据分析,计算模型的受力状态不仅要满足胞元平衡,而且要满足整个芯子平衡,即各节点平衡,图5所示为受剪力的等效模型图。在模型建立时,假设A,B,C节点没有相对位移,同时各节点转过的角度是相等的,剪切变形是由BD绕B点的转动和BD的弯曲形成的。
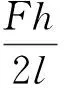
T型胞元变形及端点D的位移见图6。如图6所示,AB胞壁可看成A点和B点简支,在A点和B点均有弯矩M,则此时可由AB杆受力情况得到在B点产生的逆时针转角:
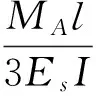


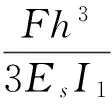
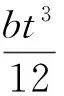
综合式(1)—式(3),对于类方形蜂窝结构有h=2l,得到利用Euler梁原理推导的类方形蜂窝夹层结构的等效力学常数为
2 基于能量法求解等效力学常数
同样,将类方形蜂窝夹芯结构分解为T型胞元结构,定义相同的尺寸要素,使用能量法原理,通过等效模型建立方程,推导具有类方形蜂窝夹芯结构特征参数的等效力学常数。
2.1 类方形蜂窝x方向等效弹性模量
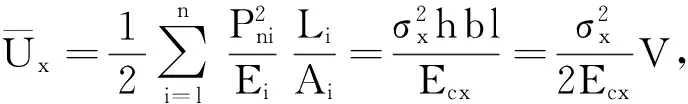
2.2 类方形蜂窝y方向等效弹性模量
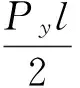

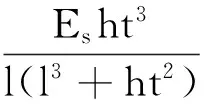
(6)
2.3 类方形蜂窝等效剪切模量
通过分析,所计算模型的受力状态既要满足类方形蜂窝胞元结构的平衡,同时也要满足整个宏观尺度下夹芯结构的平衡,即每一个节点的平衡,等效模型的受力情况如图5所示。
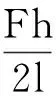
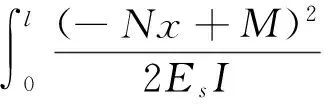
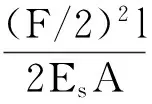
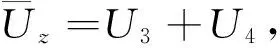
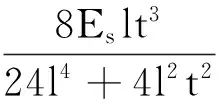
(7)
综合式(5)—式(7),对于类方形蜂窝结构有h=2l,得到利用能量法推导的类方形蜂窝夹芯结构的等效弹性常数为
(8)
对比式(4)、式(8)可知,2种方法推导得到的等效弹性模量Ecx和Ecy结果完全相同,而剪切模量Gcxy整体值近似,但在分母中多出了关于t/l的一个二次项。实际上,类方形蜂窝的胞元壁厚t远远小于胞壁壁长l,所以式(4)中的Gcxy可认为是式(8)中3+1/2(t/l)2≈3的结果。
综上所述,能量法求解得到类方形蜂窝夹芯等效力学常数的结果与用Euler梁原理求解的结果是一致的,这2种方法在理论上可以互为验证,从而保证结果的准确性。
3 类方形蜂窝与六边形蜂窝的关系
各种蜂窝夹芯形式中,传统的正六边形蜂窝用料省、制造简单、结构效率最高,从而被广泛应用于航空、包装、军事、建筑、交通等领域。正六边形蜂窝结构的力学性能、声学特性、抗震能力也是学者研究的热点[19-22]正六边形蜂窝和类方形蜂窝见图7。作为最早研究蜂窝结构的学者,GIBSON等[12]系统地提出了胞元材料理论,在分析时将蜂窝夹芯层结构简化为线弹性 Bernoulli-Euler 梁,忽略了胞壁在方向和向厚度的不一致性,采用固体力学理论推导出解析式。尽管该方法会给理论研究带来一定的误差,但是目前有关蜂窝夹芯结构的等效力学常数的研究工作绝大部分都是在此基础上展开的。
GIBSON推导出的蜂窝夹芯结构等效力学常数被人们称为GIBSON公式,其是研究蜂窝夹芯结构力学性能的经典理论公式。在此基础上,根据结构特点,BURTON等[13]给出修正后的双壁厚六边形蜂窝的GIBSON公式:
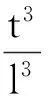
(9)
式中设定值:β=h/l,如图8所示,h为直边的长度,l为斜边的长度,t为胞元壁板的厚度,Es为制作蜂窝材料的弹性模量,θ为直边与斜边的夹角。
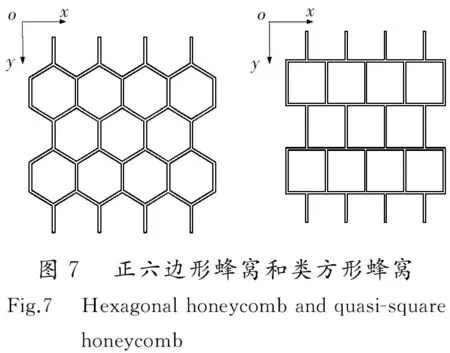

虽然反映蜂窝材料等效弹性参数的GIBSON公式结果简单,便于应用,但由于对应于蜂窝壁板伸缩变形的刚度被忽略,导致对蜂窝夹层结构数值进行分析时芯层材料的弹性矩阵表现出不确定性。富明慧等[14]重新考虑了蜂窝壁板的伸缩变形对面内刚度的影响,对GIBSON公式进行了修正,得到了富明慧公式:
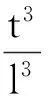
(10)
在经典蜂窝理论公式(9)和公式(10)中,蜂窝特征角θ、相邻边长比β是反应蜂窝结构形状特征的变量,其取值是根据蜂窝结构形状确定的,如正六边形蜂窝,θ=60°,β=1。经过比较(见图8)发现,当蜂窝夹芯的特征角θ=0°、相邻边长比β=2时,蜂窝夹芯可演变成类方形蜂窝夹芯。由此可认为类方形蜂窝夹芯结构是蜂窝夹芯结构的特征参数变化时的一种特殊结构,包含在蜂窝结构体系中,是蜂窝结构的一种演变体。
因此,经典蜂窝结构的理论研究成果可以直接应用到类方形蜂窝结构的研究中。然而研究发现,把类方形蜂窝夹芯结构特征参数(θ=0°,β=2)直接代入到经典蜂窝理论公式(9)和公式(10)中,会出现等效弹性常数为零或者无穷大的奇异值,这明显是不合理的。
为了应用蜂窝夹芯的等效力学常数公式,直接求解类方形蜂窝夹芯的等效力学常数,将式(10)中的Ecx和Ecy作进一步的等价变换,得到:

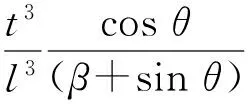
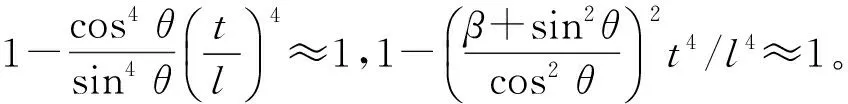
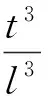
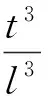
(11)
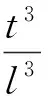
对于类方形蜂窝夹芯结构,有θ=0°,β=2,将其代入式(11)中,得到:
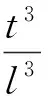
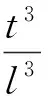
(12)
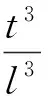
式(12)与式(4)、式(8)的结果相同,所以根据经典蜂窝力学理论公式也推理得到了类方形蜂窝夹芯结构的等效力学常数,进一步从理论上证明了类方形蜂窝结构是蜂窝结构的演变体,其与正六边形蜂窝等结构的属性相似。
类方形蜂窝结构具有一个显著特征就是蜂窝特征角θ=0°。根据Euler梁方法和能量法推导的结果可知,类方形蜂窝结构等效力学常数存在合理的准确值。而GIBSON公式、富明慧公式在蜂窝特征角θ=0°处的值是奇异的。由于类方形蜂窝结构是一个连续的物理实体,其弹性模量Ecx(θ)和Ecy(θ)均是关于θ的连续函数,所以2个经典蜂窝公式在特征角等于零附近的值都是奇异和不准确的,这说明经典蜂窝理论公式有自己的应用范围和局限性。
3 结 语
应用Euler梁方法、能量法和经典蜂窝力学理论公式,分别求解了类方形蜂窝结构的3个重要力学性能参数。Euler梁方法、能量法的求解结果均与经典蜂窝力学理论公式的求解结果相同,说明类方形蜂窝结构是六边形蜂窝结构的演变体,它与六边形蜂窝结构的属性相似。本文同时发现,GIBSON公式、富明慧公式在蜂窝特征角等于零及零附近的值为零或无穷大,这种奇异和不准确的现象与实际情况不符,指出这2个经典蜂窝公式存在局限性和应用范围。
本文的不足之处是偏重于对类方形蜂窝结构力学性能的理论研究,因此需要用实验进一步验证和完善。未来的研究方向是类比经典六边形蜂窝结构,需继续探究类方形蜂窝结构在扭转、剪切等受力状态下的承载性能,以及其屈曲、失稳等变形过程。
/
[1] 程文礼,袁超,邱启艳,等. 航空用蜂窝夹层结构及制造工艺[J]. 航空制造技术,2015(7): 94-98.
CHEN Wenli, YUAN Chao, QIU Qiyan, et al. Honeycomb sandwich structure and manufacturing process in aviation industy [J]. Aeronautical Manufacturing Technology, 2015(7):94-98.
[2] 杜正兴,薛应举,刘洪权. 复合材料蜂窝夹层结构的总体稳定性研究[J]. 强度与环境,2014,41(4):
DU Zhengxing,XUE Yingju,LIU Hongquan. General stability research of honeycomb sandwich structure[J]. Structure & Environment Engineering, 2014, 41(4).
[3] 刘均. 方形蜂窝夹层结构振动与冲击响应分析[D]. 武汉:华中科技大学, 2009.
LI Jun. Analysis of Vibration and Shock Response of Sandwich Structures with Square Honeycomb Core[D].Wuhan:Huazhong University of Science & Technology,2009.
[4] 刘均, 程远胜. 考虑芯层离散特性的方形蜂窝夹层板自由振动分析[J]. 固体力学学报, 2009, 30(1): 90-94.
LIU Jun, CHENG Yuansheng. Free vibration analysis of square-honeycomb sandwich plates considering discrete characteristic of the core [J]. Acta Mechanica Solida Sinica, 2009,30(1): 90-94.
[5] 刘敏,韩宝坤,鲍怀谦,等. 蜂窝晶胞角度对芯层材料力学性能的影响[J].声学技术,2014, 33(4): 65-68.
LIU Min, HAN Baokun, BAO Huaiqian, et al. Effect of cell angles on material mechanical properties of honeycomb core [J]. Technical Acoustics, 2014, 33(4): 65-68.
[6] 李响, 周幼辉, 童冠,等. 超轻多孔类蜂窝夹心结构创新构型及其力学性能[J]. 西安交通大学学报, 2014, 48(9): 88-94.
LI Xiang, ZHOU Youhui, TONG Guan, et al. Innovating configuration and mechanical properties of the core for ultralight and porous quasi-honeycomb sandwich structure[J].Journal of Xi’an Jiaotong University, 2014, 48(9): 88-94.
[7] 李响,周幼辉, 童冠. 一种类方形蜂窝夹层结构[P].中国专利:ZL201520147878.8, 2015-03-16.
[8] 李响, 周幼辉, 童冠. 类蜂窝结构的共面冲击特性研究[J]. 西安交通大学学报, 2017, 51(3):80-86.
LI Xiang, ZHOU Youhui, TONG Guan. Study on in-plane impact characteristics of quasi-honeycomb structure [J]. Journal of Xi’an Jiaotong University, 2017, 51(3): 80-86.
[9] 李响, 童冠, 周幼辉. 超轻多孔“类蜂窝”夹层结构材料设计方法研究综述[J]. 河北科技大学学报, 2015,36(1):16-22.
LI Xiang, Tong Guan, ZHOU Youhui. Overview of design method of class-honeycomb sandwich structure[J]. Journal of Hebei Univer-sity of Science and Technology, 2015,36(1): 16-22.
[10] GIBSON L J. Modelling the mechanical behavior of cellular material [J]. Master Science and Engineering,1989,A110:1-36.
[11] GIBSON L J,ASHBY M F,SCHAJER G S. The mechanics of two dimension celluar matericals [J]. Proceeding of the Royal Society, 1982, 382(1782):25.
[12] GIBSON L J,ASHBY M F. Cellular Solids: Structure and Properties[M]. Cambridge:Cambridge University Press, 1999.
[13] BURTON W, NOOR A K. Assessment of continuum models for sandwich panel honeycomb cores [J]. Comput Methods Appl Mech Eng,1997,145(3/4):341-360.
[14] 富明慧, 尹久仁. 蜂窝芯层的等效弹性参数[J]. 力学学报,1999, 31(1):113-118.
FU Minghui, YIN Jiuren. Equivalent elastic parameters of the honeycomb core [J]. Acta Mechanica Sinica, 1999, 31(1): 113-118.
[15] 富明慧, 徐欧腾, 陈誉. 蜂窝芯层的等效参数研究综述[J]. 材料导报,2015, 29(3):127-134.
FU Minghui, XU Ou’teng, CHEN Yu. An overview of equivalent parameters of honeycomb cores [J]. Journal of Materials Research, 2015, 29(3): 127-134.
[16] WARREN W E, KRAYNIK A M. Foam mechanics: The linear elastic response of two-dimensional spatially periodic cellular materials [J]. Mechanics of Materials, 1987, 6:27-37.
[17] 蔡四维. 复合材料结构力学[M]. 北京:人民交通出版社, 1987.
[18] 中国科学院力学研究所. 夹层板壳的弯曲、稳定和振动[M]. 北京:科学出版社,1977.
[19] WANG Shengchun, DENG Zhaoxiang, SHEN Weidong. Sound transmission loss characteristics of unbounded orthotropic sandwich panels in bending vibration considering transverse shear deformation [J]. Composite Structures,2010, 92: 2885-2889.
[20] 孙德强, 张卫红. 双壁厚蜂窝铝芯的共面冲击力学性能[J]. 振动与冲击, 2008, 27(7):69-74.
SUN Deqiang, ZHANG Weihong. In-plane impact properties of aluminum double-walled honeycomb cores [J]. Journal of Vibration and Shock, 2008, 27(7): 69-74.
[21] 韩啸,金勇,杨鹏. 结构胶接接头湿热环境耐久性研究概述[J]. 河北科技大学学报, 2017,38(3):209-217.
HAN Xiao,JIN Yong,YANG Peng. Review of research on the hygrothermal environmental durability of structural adhesively bonded joints [J]. Journal of Hebei University of Science and Technology, 2017,38(3):209-217.
[22] HADICKE E, RIEGER J, RAU I U, et al. Molecular dynamics simulations of the incrustation inhibition by polymeric additives[J]. Physical Chemistry Chemical Physics, 1999, 1(17): 3891-3898.
Mechanic properties analysis of quasi-square honeycomb sandwich structure′s core
TONG Guan1, LI Xiang2,3, MEI Yueyuan3, ZHOU Youhui3
(1. Fujian Electric Power Transmission & Transformation Engineering Company Limited, Fuzhou, Fujian 350013, China; 2. Hubei Key Laboratory of Hydroelectric Machinery Design & Maintenance, China Three Gorges University, Yichang, Hubei 443002, China;3. College of Mechanical and Power Engineering, China Three Gorges University, Yichang, Hubei 443002, China)
In order to illustrate the relationship between the quasi-square-honeycomb structure and the hexagonal honeycomb structure, after decomposing the quasi-square honeycomb sandwich structure into unique T-shaped cell, the equivalent elastic constants equations of T-shaped cell model are derived respectively by applying Euler beam theory and energy method. At the same time, the quasi-square honeycomb's characteristic structure parameters are substituted into the equivalent elastic constants equations which are derived by the classical method of a hexagonal honeycomb core, and the same results are obtained as that of the preceding both methods. It is proved that the quasi-square-honeycomb structure is an evolution of hexagonal honeycomb. The limitations and application scope of the two classical honeycomb formulas are pointed out. The research of the structural characteristics of the square-shaped honeycomb shows that the classical cellular theoretical formula are singular and inaccurate when the feature angle values equal to zero or near zero. This study has important reference value for the subsequent research and improvement of the theories about cellular structure mechanical properties.
structural mechanics; sandwich structure; quasi-square honeycomb; energy method; equivalent elastic constant; mechanical property
1008-1542(2017)06-0522-08
10.7535/hbkd.2017yx06003
TB333
A
2017-05-31;
2017-09-17;责任编辑:张士莹
国家自然科学基金(51305232)
童 冠(1990—),男,湖北黄冈人,硕士,主要从事结构轻量化设计方面的研究。
李 响副教授。E-mail:lixiangcfy@163.com
童 冠,李 响,梅月媛,等.类方形蜂窝夹芯结构力学性能研究[J].河北科技大学学报,2017,38(6):522-529.
TONG Guan,LI Xiang,MEI Yueyuan,et al.Mechanic properties analysis of quasi-square honeycomb sandwich structure′s core[J].Journal of Hebei University of Science and Technology,2017,38(6):522-529.

