线黏弹性球面发散应力波的频率响应特性*
卢 强,王占江,丁 洋,刘晓新,郭志昀,吴玉蛟
线黏弹性球面发散应力波的频率响应特性*
卢 强1,2,王占江1,丁 洋1,刘晓新1,郭志昀1,吴玉蛟1
(1.西北核技术研究所,陕西 西安710024;2.西安交通大学航天学院机械结构强度与振动国家重点实验室,陕西 西安710049)
基于线黏弹性球面波Laplace域的理论解,得到了不同传播距离处粒子速度、粒子位移、应力、应变等力学量的传递函数。以标准线性固体模型为例,重点讨论了粒子速度频率响应函数的传播特征,指出随着传播距离的增加,粒子速度幅频响应函数的高频响应会低于低频响应,而在理想弹性条件下,粒子速度幅频响应函数的高频响应一直高于低频响应。以弹性半径为0.025m的空腔爆炸为例,采用Laplace数值逆变换方法对粒子速度波形的演化进行了分析,给出了粒子速度强间断幅值及粒子速度峰值随传播距离变化的衰减规律曲线,指出黏弹性介质中粒子速度幅值的衰减曲线介于理想弹性介质中粒子速度幅值衰减曲线和黏弹性介质中粒子速度强间断幅值衰减曲线之间。
球面应力波;频率响应;拉普拉斯逆变换
在地震或地下爆炸激发的地震波传播研究中,具有一定压力边界的有限球形空腔可以视为震源,因此固体介质中的球面应力波传播理论对于研究地震或地下爆炸的震源特征、应力波的传播演化规律等具有重要作用。F.G.Blake[1]和 H.L.Selberg[2]基于折合位移势(reduced displacement potential,RDP)给出了理想弹性球面波传播的处理方法。RDP是球面波波动方程的一个解,球面波传播中涉及到的粒子速度、粒子位移、应力、应变等物理量均可通过RDP给出。H.C.Rodean[3]研究了理想弹性介质中球形发散压缩波的传播,并讨论了球形发散应力波的特征频率(周期、波长)及其衰减规律。H.C.Rodean的工作对理想弹性球面应力波的传播规律进行了完整的总结。由于波传播和材料的动态力学性能相关,研究者们基于不同的本构方程(弹塑性[4-8]、弹黏塑性[9-11]、Maxwell体[12]和 Kelvin-Voigt体[13]黏弹性、线性和非线性ZWT[14-20]等)对球面应力波的传播特征进行了分析,进一步完善了球面波传播理论。
在考虑介质的黏弹性条件下,从震源辐射出的波频率特征和理想弹性条件下波的传播特征不同。为深入研究黏弹性球面应力波的频率响应特性随传播距离的变化特征,本文中基于线黏弹性球面波Laplace域的理论解[19],得到不同传播距离处粒子速度、应力、应变等物理量的传递函数,并以标准线性固体模型为例,重点讨论粒子速度频率响应函数的传播特征。以弹性半径为0.025m的空腔爆炸为例,采用Laplace数值逆变换方法[21]对粒子速度波形的演化进行分析,给出粒子速度强间断幅值及粒子速度峰值随传播距离变化的衰减曲线。
1 线黏弹性球面应力波的频率响应函数
无限介质中线黏弹性球面波的Laplace解可按如下方程计算[19]:



令s=ωi(ω=2πf为圆频率,f为频率,i为虚数单位),则公式(7)表征不同物理量传递函数对应的频率响应函数。需注意的是,上面的分析中并没有基于特定的线黏弹性本构模型,即上述公式具有分析线黏弹性球面发散应力波的普适性。
2 基于标准线性固体模型的粒子速度频率响应函数传播特征
在地下爆炸或地震研究中,地运动信号(粒子加速度、速度、位移)是常见的分析对象,因此本文中仅对粒子速度的频率响应函数进行讨论(理论上粒子加速度、速度、位移的频率响应函数相同)。粒子速度的频率响应函数可以写为:

线黏弹性球面应力波的传播系数β(ωi)可以写为:

式中:α(ω)为线黏弹性球面应力波衰减因子,k(ω)为线黏弹性球面应力波的波数(k(ω)=ω/c(ω),c(ω)为线黏弹性球面应力波的相速度)。把公式(9)代入公式(8),则有:
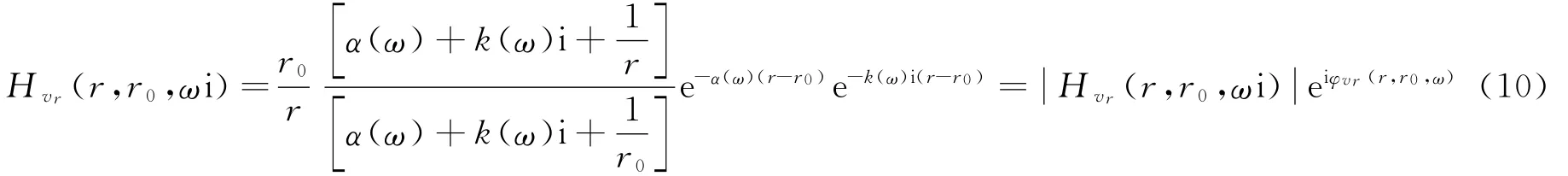
式中: Hvr(r,r0,ωi)和φvr(r,r0,ω)分别为粒子速度响应函数的幅频特性和相频特性,其表达式可以写为:

公式(12)中Φ(r,ω)满足下式:


图1 标准线性固体模型Fig.1Standard linear solid model
本文中基于标准线性固体模型展开对粒子速度频率响应函数传播特征的讨论。标准线性固体模型由1个线性弹簧和1个Maxwell体并联而成,如图1所示。此模型的复体积模量K~(s)和复剪切模量G~(s)可以写为:

式中:μ为泊松比,E0和E1分别为线性弹簧和Maxwell体中弹簧的弹性模量,K0和K1分别为对应的体积模量,G0和G1分别为对应的剪切模量,θ1为Maxwell体的松弛因子。令s=ωi=2πfi,把公式(14)~ (15)代入公式(9),可以给出衰减因子α(f)和波数k(f)的解析式[20]。由文献[20],当f→"时(对应高频状态):
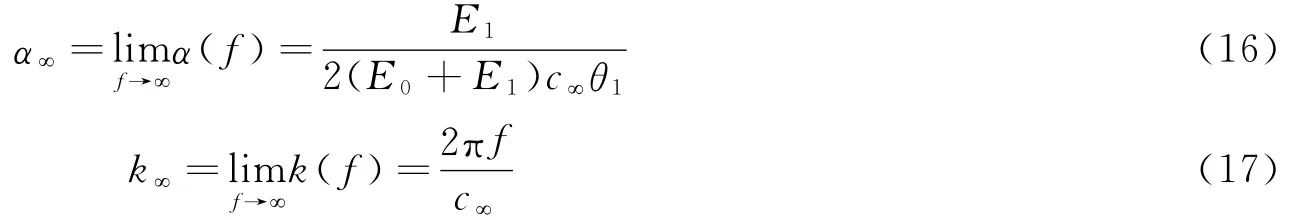
式中:c"代表高频体波波速,可以写为:
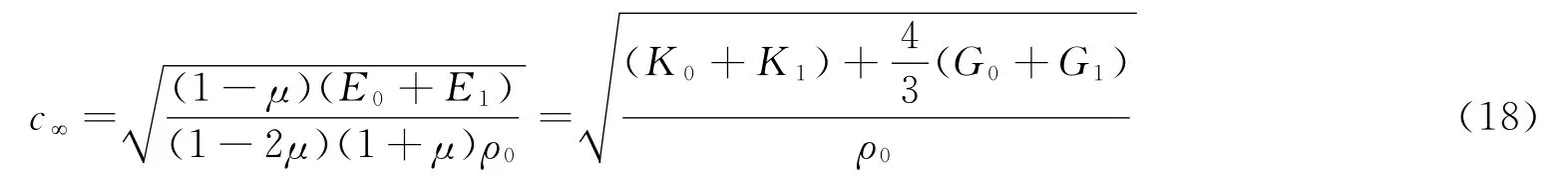
当f→0时(对应低频状态):
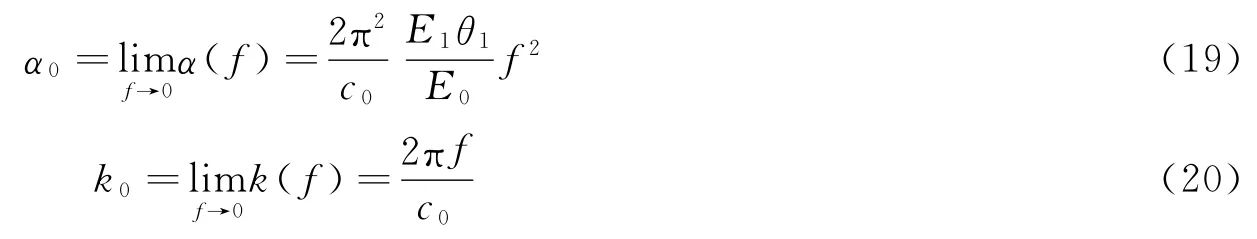
式中:c0代表低频体波波速,可以写为:

结合公式(11)、(16)~(21),当f→"时,有:

当f→0时,有:

当公式(22)~(23)满足下式时:

速度响应函数对高频和低频的响应相同,通过整理公式(24),有:

定义函数χ(r),有:

如图2所示,函数χ(r)在r∈ (0,α-"1]区间内是递增函数,在r∈ [α-"1,")区间内是递减函数,在r=α-"1处取得极大值。存在下述两种情况:(1)当r0≤α-"1时,在r∈ [α-"1,")区间内存在r1满足式(25),使得高频幅频响应和低频幅频响应相同。在r∈[r0,r1]区间内高频幅频响应高于低频幅频响应,在r∈(r1,")区间内高频幅频响应低于低频幅度响应;(2)当r0>α-"1时,在r∈ [r0,")区间内当且仅当r1=r0时满足公式(25),由此可知在r∈(r0,")区间内高频幅频响应均低于低频幅频响应。
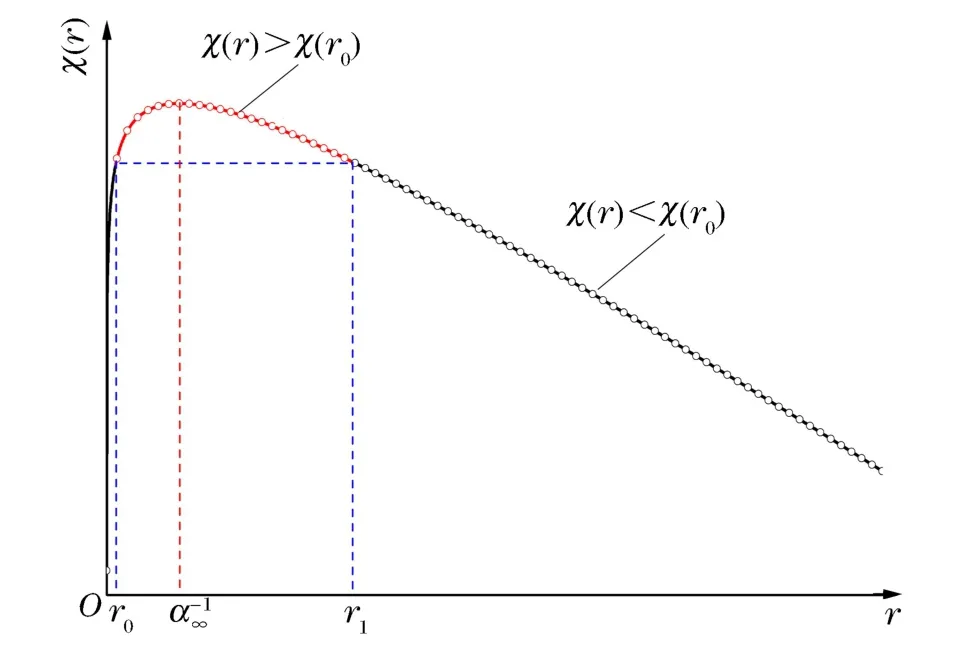
图2 函数χ(r)随r的变化Fig.2Functionχ(r)vs.r
以黄土标准线性固体模型参数(如表1中所示)为例,此时α"≈3.55m-1(α-"1≈0.282m)。图3给出了弹性半径r0=0.025m(r0≤α-"1)时粒子速度频率响应函数随传播距离的变化,可以看出,图3中曲线符合上述第一种情况的描述。当r>r1=r0>α-"1时,其粒子速度频率响应函数和图3中r=2.5m时的曲线类似,高频幅频响应均低于低频幅频响应,在频率f0(定义为卓越频率)处使得幅频响应取得最大值,频率f1(定义为上限频率,高于此频率的幅频响应均低于低频幅频响应,即信号幅频响应主要集中在上限频率以下)处的幅频响应等于低频幅频响应。
图4给出了弹性半径r0分别为0.025、0.25、2.5、25和250m时卓越频率f0和上限频率f1随传播距离的变化。对于特定场地的地下填实爆炸来说,弹性半径的大小和爆炸当量相关,爆炸当量越大则弹性半径越大。从图4中可以看出,f0和f1随着传播距离的增加而减小,爆炸当量越大,卓越频率f0和上限频率f1越小。为对比近区和远区粒子速度响应函数的频率特征,表2给出了不同弹性半径时0.5和1 000km处的卓越频率f0和上限频率f1。弹性半径为0.025~25m时,在接近1 000km传播距离处,此4条曲线在图4中基本重合,表2中的数据也证实了这一点,其卓越频率f0在2.33~2.48Hz之间,上限频率f1在11.32~11.71Hz之间。可以看出不同弹性半径下,上限频率f1的变化率比卓越频率f0要小。弹性半径为25m时对应的爆炸当量是弹性半径为0.025m时爆炸当量的109倍,而在1 000km处粒子速度频率响应函数的卓越频率f0和上限频率f1基本一致,这说明当波的传播距离据爆心足够远时爆炸当量对地震信号的频谱特性没有显著影响。图4中弹性半径为250m时的频率曲线在1 000km处卓越频率f0为1.19Hz、上限频率f1为10.09Hz。从变化趋势上看,若传播距离继续增加,弹性半径为250m时的频率曲线会和弹性半径分别为0.025、0.25、2.5、25m的4条频率曲线更加接近。
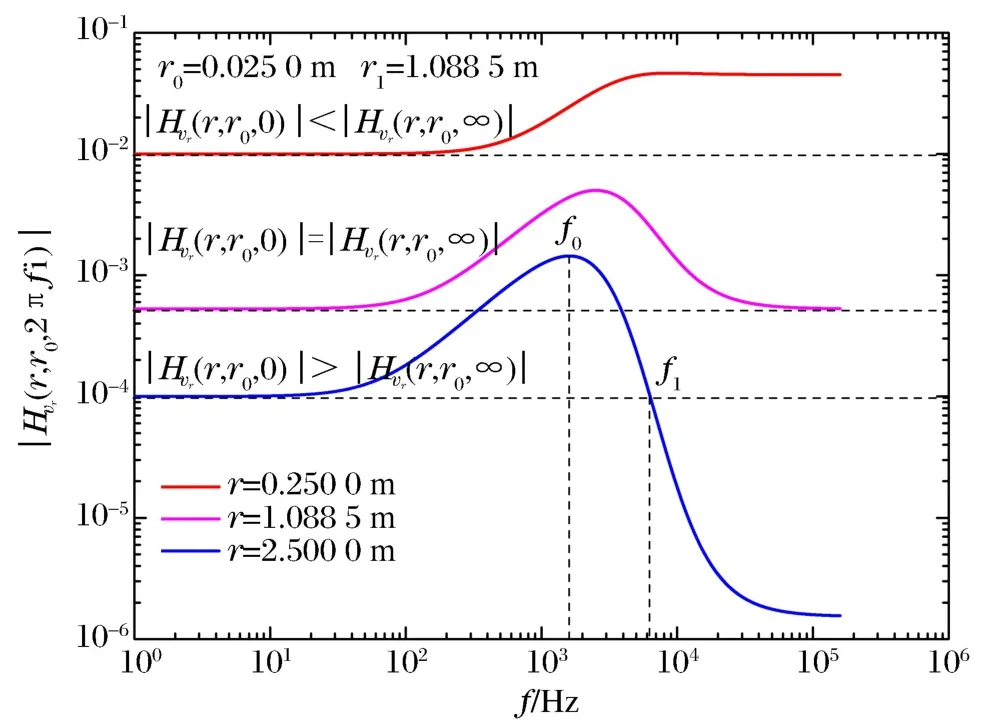
图3 幅频响应函数 Hvr(r,r0,2πfi)随频率f 的变化Fig.3Amplitude-frequency response function Hvr (r,r0,2πfi)vs.frequencyf

图4 卓越频率f0和上限频率f1随传播距离r的变化Fig.4Predominant frequency f0and upper limit frequency f1 varying with propagation distance r

表1 黄土材料标准线性固体模型参数Table 1Parameters of the standard linear solid model for loess

表2 卓越频率f0和上限频率f1的变化Table 2Variations of predominant frequency f0and upper limit frequency f1
3 粒子速度波形的演化
前面对不同位置粒子速度的频率响应函数特征进行了讨论,下面就粒子速度的波形演化特征进行数值模拟分析,主要是研究强间断及粒子速度幅值随传播距离的变化规律。模拟中采用黄土作为示例材料(材料参数如表1所示),弹性半径取为0.025m,假设空腔边界的压力形式为:

式中:σd+σs为空腔边界上施加压力的强间断幅值,σs为稳态空腔压力,t0为压力的延迟时间。取σd=σs=1MPa,t0=21μs。

图5不同位置的粒子速度波形Fig.5Particle velocity histories at different locations
图5 给出了0.025~4.775m区域内不同位置处的粒子速度波形。由公式(18)和表1,可以给出c"=1 134.3m/s。由于空腔边界处施加了强间断压力边界条件,在空腔边界上粒子速度的强间断幅值vviscor_sd(r0)可以写为:
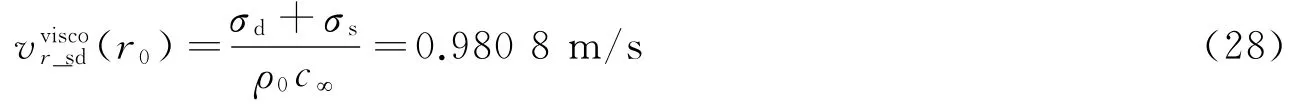
粒子速度强间断幅值vviscor_sd(r)可以写为[19]:

通过图5可以看出,粒子速度强间断幅值衰减很快,在图5(c)中,r≥2.275m处粒子速度强间断幅值已经几乎观察不到了,这主要是高频波衰减快造成的。在本文中给出的计算区域内,含有强间断的粒子速度波形逐渐演化为具有一定上升时间的波形。这里需要指出,即使r≥2.275m处的粒子速度强间断从视觉上观察不到,但理论上是存在的。另外,通过图5还可以看出,当r≥0.775m时,粒子速度强间断幅值不再是粒子速度波形的峰值,这主要是因为不同位置处粒子速度的幅频响应函数对不同频率的波响应不同,这些位置处高频波的幅频响应不是整个幅频响应曲线的峰值。
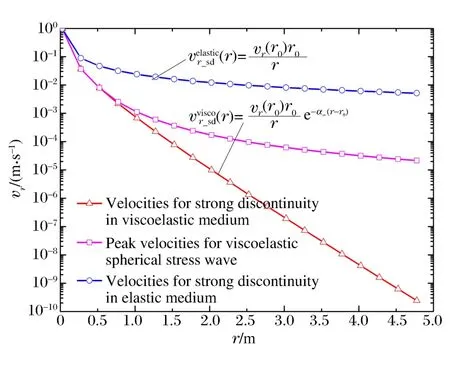
图6粒子速度峰值(强间断幅值)随传播距离r变化Fig.6Peak values of particle velocity vs.propagation distance r
图6 给出了黏弹性黄土介质中粒子速度峰值、强间断幅值随传播距离的变化规律。作为对比,图6还给出了理想弹性材料中粒子速度峰值随传播距离的变化规律(理想弹性材料中粒子速度强间断幅值和粒子速度峰值相等)。从图6可以看出,黏弹性介质中粒子速度幅值的衰减曲线介于理想弹性介质中粒子速度幅值衰减曲线和黏弹性介质中粒子速度强间断幅值衰减曲线之间。在近区,理想弹性材料中粒子速度强间断幅值衰减曲线(仅有几何扩散效应)和黏弹性介质中粒子速度峰值(或强间断幅值)的衰减曲线的偏离程度较小,而随着波传播距离的增加,两者的偏离程度加大。这说明:(1)在近区,球面波的几何扩散效应对粒子速度峰值(或强间断幅值)的衰减起主导作用;(2)在远区,介质的黏性对粒子速度峰值(或强间断幅值)的衰减起主导作用。
4 结 论
基于球面发散应力波在Laplace域的理论解,得到了不同传播距离处粒子速度、应力、应变等物理量的传递函数,并以标准线性固体模型为例,重点讨论了粒子速度的频率响应函数的传播特征,给出了卓越频率和上限频率随传播距离变化的曲线。以弹性半径为0.025mm的空腔爆炸为例,采用Laplace数值逆变换方法对粒子速度波形的演化进行了模拟。基于上述分析,得出如下结论:
(1)黏弹性球面波的幅频响应函数除了和弹性半径r0及传播距离r有关之外,还和黏弹性本构引入的本构衰减有关。理想弹性球面波的幅频响应函数仅和弹性半径r0及传播距离r有关;
(2)在线黏弹性条件下,当弹性半径r0≤α-"1时,随着球面波传播距离的增加,粒子速度幅频响应函数的高频响应会由高于低频响应状态过渡到低于低频响应状态。当弹性半径r0>α-"1时,无论球面波传播距离如何变化,粒子速度幅频响应函数的高频响应永远低于低频响应;
(3)黏弹性介质中粒子速度幅值的衰减曲线介于理想弹性介质中粒子速度幅值衰减曲线和黏弹性介质中粒子速度强间断幅值衰减曲线之间。在近区,球面波的几何扩散效应对粒子速度峰值(或强间断幅值)的衰减起主导作用。在远区,介质的黏性对粒子速度峰值(或强间断幅值)的衰减起主导作用。
[1] Blake F G.Spherical wave propagation in solid media[J].Journal of the Acoustical Society of America,1952,24(2):211-215.
[2] Selberg H L.Transient compression waves from spherical and cylindrical cavities[J].Arkiv for Fysik,1952,5(1/2):97-108.
[3] Rodean H C.Elastic wave radiation from spherical sources.UCRL-52867[R].Lawrence Livermore Laboratory,1979.
[4] Garg S K.Spherical elastic-plastic waves[J].Journal of Applied Mathematics and Physics,1968,19(2):243-251.
[5] Garg S K.Numerical solutions for spherical elastic-plastic wave propagation[J].Journal of Applied Mathematics and Physics,1968,19(5):778-787.
[6] 李孝兰.空腔解耦爆炸实验研究的理论基础(Ⅰ)[J].爆炸与冲击,2000,20(2):186-192.Li Xiaolan.Basic theory of decoupled explosions in cavities(Ⅰ)[J].Explosions and Shock Waves,2000,20(2):186-192.
[7] 李孝兰.空腔解耦爆炸实验研究的理论基础(Ⅱ)[J].爆炸与冲击,2000,20(3):283-288.Li Xiaolan.Basic theory of decoupled explosions in cavities(Ⅱ)[J].Explosions and Shock Waves,2000,20(3):283-288.
[8] 卢强,王占江,门朝举,等.有机玻璃中球形应力波传播的分析[J].爆炸与冲击,2013,33(6):561-566.Lu Qiang,Wang Zhanjiang,Men Chaoju,et al.Analysis of spherical stress save propagating in PMMA[J].Explosion and Shock Waves,2013,33(6):561-566.
[9] Perzyna P.On the propagation of stress waves in a rate sensitive plastic medium[J].Journal of Applied Mathematics and Physics,1963,14(3):241-261.
[10] Phillips A,Zabinski M P.Spherical wave propagation in a viscoplastic medium[J].Ingenieur Archiv,1972,41(6):367-376.
[11] Zabinski M P,Phillips A.Spherical wave propagation in a viscoplastic medium-the case of unloading[J].Acta Mechanica,1974,20(3):153-166.
[12] Koshelev E A.Spherical stress wave propagation during an explosion in a viscoelastic medium[J].Soviet Mining,1988,24(6):541-546.
[13] Banerjee S,Roychoudhuri S K.Spherically symmetric thermo-visco-elastic waves in a visco-elastic medium with a spherical cavity[J].Computers & Mathematics with Applications,1995,30(1):91-98.
[14] Wang L L,Lai H W,Wang Z J,et al.Studies on nonlinear visco-elastic spherical waves by characteristics analyses and its application[J].International Journal of Impact Engineering,2013,55(1):1-10.
[15] 赖华伟,王占江,杨黎明,等.线性黏弹性球面波的特征线分析[J].爆炸与冲击,2013,33(1):1-10.Lai Huawei,Wang Zhanjiang,Yang Liming,et al.Characteristics analyses of linear viscoelastic spherical waves[J].Explosion and Shock Waves,2013,33(1):1-10.
[16] 赖华伟,王占江,杨黎明,等.由球面波径向质点速度实测数据反演材料黏弹性本构参数[J].高压物理学报,2013,27(2):245-252.Lai Huawei,Wang Zhanjiang,Yang Liming,et al.Inversion of constitutive parameters for viscoelastic materials from radial velocity measurements of spherical wave experiments[J].Chinese Journal of High Pressure Physics,2013,27(2):245-252.
[17] 卢强,王占江,李进,等.球面波加载下黄土线黏弹性本构关系[J].岩土力学,2012,33(11):3292-3298.Lu Qiang,Wang Zhanjiang,Li Jin,et al.Linear viscoelastic constitutive relation of loess under spherical stress wave[J].Rock and Soil Mechanics,2012,33(11):3292-3298.
[18] 卢强,王占江,王礼立,等.基于ZWT方程的线黏弹性球面波分析[J].爆炸与冲击,2013,33(5):463-470.Lu Qiang,Wang Zhanjiang,Wang Lili,et al.Analysis of linear visco-elastic spherical wave based on ZWT constitutive equation[J].Explosion and Shock Waves,2013,33(5):463-470.
[19] 卢强,王占江.标准线性固体材料中球面应力波传播特征研究[J].物理学报,2015,64(10):108301.Lu Qiang,Wang Zhanjiang.Characteristics of spherical stress wave propagation in the standard linear solid material[J].Acta Physica Sinica,2015,64(10):108301.
[20] Lu Qiang,Wang Zhanjiang.Studies of the propagation of viscoelastic spherical divergent stress waves based on the generalized Maxwell model[J].Journal of Sound and Vibration,2016,371(1):183-195.
[21] Crump K S.Numerical inversion of Laplace transforms using a Fourier series approximation[J].Journal of the Association for Computing Machinery,1976,23(1):89-96.
Characteristics of frequency response for linear viscoelastic spherical divergent stress waves
Lu Qiang1,2,Wang Zhanjiang1,Ding Yang1,Liu Xiaoxin1,Guo Zhiyun1,Wu Yujiao1
(1.Northwest Institute of Nuclear Technology,Xi’an 710024,Shaanxi,China;2.State Key Laboratory for Strength and Vibration of Mechanical Structures,School of Aerospace,Xi’an Jiaotong University,Xi’an 710049,Shaanxi,China)
In this study the transfer functions of the mechanical quantities(i.e.the particle velocity,the particle displacement,the stress and the strain,etc.)at different propagation distances were analytically presented based on the solutions of the linear viscoelastic spherical stress wave in the Laplace domain,The propagating characteristics of the frequency response function for the particle velocity were examined with the standard linear solid model taken as an example.The results reveal that the high-frequency response of the frequency response function for the particle velocity in viscoelastic medium is less than that of the low-frequency response with the increase of the propagation distance;in an ideal elastic medium,however,it is always greater than that of the low-frequency response.With the cavity explosion with the elastic radius of 0.025mtaken as an example,the evolution of the wave form of the particle velocity was calculated using the numerical method of the inverse Laplace transform.The results reveal that the attenuation curve of the peak value for the particle velocity in viscoelastic medium falls in between the attenuation curve of the the peak value for the particle velocity in an ideal elastic medium and the attenuation curve of the amplitude of the strong discontinuity for the particle velocity in viscoelastic medium.
spherical stress waves;frequency response;Laplace inversion transform
O347.4 国标学科代码:13015
A
10.11883/1001-1455(2017)06-1023-08
2016-04-21;
2017-01-07
国家自然科学基金项目(11172244)
卢 强(1984— ),男,博士研究生;通信作者:王占江,wangzhanjiang@nint.ac.cn。
(责任编辑 曾月蓉)

