基于等效路径的爆破地震波衰减规律*
胡学龙,璩世杰,蒋文利,李 华,杨 威,黄汉波,胡光球
基于等效路径的爆破地震波衰减规律*
胡学龙1,璩世杰1,蒋文利2,李 华2,杨 威2,黄汉波2,胡光球1
(1.北京科技大学土木与环境工程学院,北京100083;2.河北钢铁集团矿业公司,河北 唐山063000)
针对露天矿山台阶爆破地形和地质条件的复杂性,分析了地形对爆破地震波传播路径的影响,提出了等效路径及等效距离两个概念。同时考虑岩石波阻抗和岩体的完整性系数及最大一段装药量与炸药的定容爆热等因素的影响,构建了露天台阶爆破地震波地表质点振速峰值随等效距离衰减的表达式。通过矿山爆破震动监测检验,发现用该公式预测地表质点振速峰值,能够适应实际地形和地质条件的变化,预测结果的准确性显著高于萨氏公式,表明该公式较好地反映了质点振速峰值沿等效路径衰减的基本规律,为台阶爆破地震波质点振速峰值预测提供了一种新方法。
爆破;地震动;振速峰值;地形;等效路径
爆破引起的地震动是各种岩土爆破工程都会产生的一种有害效应,可对矿山边坡的稳定、一定范围内建构筑物的安全等造成不利影响。因此,在实施爆破工程之前对爆破震动效应进行准确预测,对控制或避免爆破震动危害具有重要意义。
目前的研究普遍将质点振动速度作为表述爆破地震波衰减规律的一个主要指标,其影响因素主要包括药量、埋深、爆破方式等爆源因素以及爆心距、传播途径、岩土条件等。在预测爆破振动效应时,全面和准确地考虑这些因素的影响是非常困难的,因此通常采用萨氏公式v=K(QnR-1)-α[1]或比例距离公式v=K(SD)-β[2]等经验公式来反映爆破地震波随距离的衰减规律,并用以预测质点振速峰值。其中Q为爆破最大一段起爆炸药量,R同为爆心距,即测点至爆区药包中心的距离,系数K、α、β是与爆破场地条件、地质条件有关的系数,SD 为比例距离(SD=RQ-n),n为与装药条件有关的系数。但是,实践中自爆源至不同方向不同距离上各测点的地形及地质条件在绝大多数情况下都存在着较大差异。研究表明:通过现场爆破震动测试获取或按岩石坚硬程度选取的K、α值预测质点振速峰值,远距离的预测误差可达50%以上,近距离爆破振动预测的误差则更大[3-7]。
本文中针对台阶爆破工程环境中地形和地质条件的多变性与复杂性,提出并运用等效路径和等效距离两个概念,尝试探索爆破地震波地表质点振速峰值随等效距离衰减的一般规律,从而建立一种对地形和地质条件具有一定普适性的爆破地震波质点振速峰值预测方法。
1 研究现状及问题
爆破产生的地震波是在地表以下的岩土体这样一种半无限介质体中逐渐向外传播的。在如图1所示的露天矿山和大多数的自然地形环境中,爆源与测点之间的地形往往呈凹凸起伏状,爆破地震波不一定能在岩石中沿一条直线传播至测点位置。根据惠更斯-菲涅耳原理[8],可认为任意地形条件下测点位置上的震动是整个地震波波前各子波向测点位置直线传播并在测点位置叠加的结果。然而,尽管这种定性的理论描述能够反映爆破地震波传播的某些本质,但迄今尚无法在严格的科学意义上对该问题给出数学上的解析解,即还不能通过波动理论给出一个能够反映复杂地形条件下质点振速峰值与爆破地震波传播距离之间关系的数学表达式。
目前仍普遍采用基于工程类比的经验公式来预测爆破震动效应。表1为比较常用的爆破振动速度预测的经验公式。

表1 爆破地表质点振速峰值预测经验公式[9]Table 1Empirical equations for prediction of blast induced peak particle velocity
采用表1中各公式及比例距离公式预测质点振速峰值,具有两个共同的重要特点:一是用若干个系数(如K和α)的值反映地质地形条件对地表质点振速峰值的影响,二是用爆心距R作为确定测点位置上质点振速峰值的一个重要因素。在我国的爆破工程实践中,通常是通过现场爆破震动测试获取或按岩石坚硬程度从相关的规程中选取K和α的值。显然,采用这种做法预测质点振速峰值,自爆源/爆区至预测点之间的地质地形条件须与选定的K和α值具有足够高的一致性,才有可能保证预测结果的准确性。但在矿山乃至其周围,爆源至不同方向不同距离上各测点的地质地形条件往往存在着各种各样或大或小的差异。在沿台阶走向方向,近距离范围内的地形一般都较为平坦,而在垂直或斜交台阶走向方向上的凹凸起伏却往往比较大(见图2)。与之同时,不同区域不同方向上的岩石种类一般也存在着不可忽略的差异。因此,尽管是在同一个矿山,任何一组选定的K、α值都无法同时有效地反映不同区域不同方向上不同地形和地质条件的影响。
另外,在露天矿山台阶爆破工程环境下,应用以上所述的经验公式时,除地形平坦的情况外,如何确定爆心距R也是一个无法回避的重要问题。在图2中,如果取爆心距R为爆源与测点之间的直线距离,就无法反映爆源与测点之间可能存在的凹陷地形对爆破地震波传播的影响。然而,如何定义类似的凹凸起伏地形条件下的爆心距,在业界尚未形成共识。
关于地形对爆破地震波传播影响的研究很多,且取得了不少积极的进展。谭文辉等[10]基于爆破振动监测,发现高程差和岩石性质对萨氏公式的K、α值都具有重要影响。张华等[11]发现应用传统的萨氏公式确定深凹露天爆破振动速度衰减规律时具有很大的误差,并提出了一个考虑高程效应等因素的修正公式。为反映高程差对爆破振动效应的影响,刘美山等[12]对萨氏公式进行了改进,提出用公式v=K(Q1/3R-1)αeβH预测质点振速峰值,式中H 为从测点到爆破中心的垂直距离,β是与地质条件有关的系数,其他参数的含义同前。朱传统等[5]认为振动速度沿高程有放大效应,因而振动速度的计算公式应为v=K (Q1/3R-1)α(Q1/3H-1),之后裴来政[13]用该公式对金堆城露天矿高边坡爆破振动效应进行了分析,认为爆破振动速度随着高程的增加存在一定的放大效应。宋光明等[7]则提出用公式v=K (Q1/3R-1)α(RS-1)来确定边坡上爆破地震波的衰减,其中R、S分别为爆心至测点的斜距和水平距离。但是,如何反映爆源与测点之间地形的变化对质点振速峰值的影响及其规律,尚需进一步的研究。
2 爆破地震波传播的等效路径
爆破地震波的传播过程即是其在地表以下的岩土体中随距离衰减的过程。对这一距离给出准确的定义,是研究爆破地震波传播距离与地表质点振速峰值之间关系以确定爆破地震波衰减规律的前提。
在其他因素都不变的前提下,可假定测点位置上的质点振速峰值取决于爆破地震波自爆源向测点传播过程中行走的最短距离。如果这一假定成立,则可以该假定作为确定任意地形条件下爆破地震波的传播路径与距离的基本准则。爆破地震波沿此路径传播的距离在形式上等效于平坦地形条件下爆源至测点的直线距离。从这个意义上讲,可将该路径称为等效路径,并将该路径的长度称为等效距离。
2.1 台阶地形下等效路径与等效距离的确定
在如图3所示的台阶地形条件下,从爆源O画一直线段至测点位置,若该直线段内有与地表面相交的现象,则地震波不能沿此直线传播到测点位置。此时爆破地震波传播的路径即等效路径的确定方法与步骤为:
(1)以最大一段装药量Q的质心O为原点作一射线(记为L0),以O为轴在地表以下向测点M 旋转L0,记L0与地表或地表面上不同岩种交界线首先相交的第1个节点为P1,则用O P1表示等效路径的第1段折线段,记其长度为R0;
(2)然后以点P1为轴向测点M 旋转L1(以P1为起点的射线),L1与地表相交的第1个节点为P2,则P1P2为等效路径的第2段折线段,记其长度为R1,并记O P1和P1P2的交角为θ1;以此类推,直至Li(以Pi为起点的射线,当i=0时,则P0即为O点)与地面相交的点为测点M。
于是,台阶地形条件下爆破地震波传播的等效距离R可表示为:
根据惠更斯-菲涅尔原理,假设波的传播方向与次波传播方向之间的夹角为θi,则波的振幅将随夹角θi的增大而减小。应用古斯塔夫·基尔霍夫给出的倾斜因子[8]:
式(1)可改写为:
式中:Ri为节点Pi至节点Pi+1的直线距离,θi为地震波传播至节点Pi处的倾斜角度。
综上所述,台阶地形条件下的等效路径即是以最大一段装药量Q的质心O为始点、以测点位置M为终点的折线,折线上的各个节点是地表面轮廓线上的拐点。
2.2 凹陷地形的等效路径与等效距离的确定
以如图4所示具有凹陷曲面的地形条件为例,以节点P1为轴向测点M 逆时针旋转垂线l,其与凹陷段地表面轮廓线相切或相交的第1点即为节点P2,然后以测点M 为轴向节点P2顺时针旋转垂线l,l与凹陷段地表面轮廓线的切点或交点即为节点P3。
基于一般的应力波传播理论,爆破地震波自节点P2传播至节点P3的过程极为复杂,难以采用理论解析的方法表征其传播的规律。对于此种情况,可采用以下步骤近似确定节点P2与节点P3之间的等效距离:
(1)自测点M 向节点P3引直线并延长,同时延长自节点P1至节点P2的直线;
(2)设二延长线的交点至地表的最短距离为B,将该距离的1/2处视为节点C;
(3)将自节点P2至节点P3凹陷地形的等效路径分为两段,各段的等效距离依次为R2和R′2。
3 基于等效路径的质点振速峰值
运用上述等效路径和等效距离的概念,同时综合考虑最大一段装药量、炸药的定容爆热、爆破地震波传播的等效距离及该距离上岩石的波阻抗和岩体完整性系数对地表质点振速峰值的影响,引入式(1)~(3),台阶爆破地表质点振速峰值与地震波传播的等效距离之间的关系可表示为:
式中:v为质点振速峰值;Q 为最大一段装药量;QV为炸药的定容爆热;Ri为节点Pi(等效路径上的拐点和岩石岩性变化的分界点)与节点Pi+1之间的等效距离;θi为地震波传播路径上节点Pi处的方向角;ρi为等效路径PiPi+1上所对应岩石的密度;cmi为等效路径PiPi+1上所对应岩体的纵波传播速度;ηi为等效路径PiPi+1上所对应岩体的完整性系数,ηi=(cm/cr)2,其中cm和cr分别为岩体和岩石的纵波传播速度;K、α为系统常数;β为对远距离台阶炮孔爆破质点振速预测,可将最大一段装药量视为集中药包,取β=1/3。
为叙述方便,以下将式(4)称为等效距离公式,应用该公式预测不同地形地质条件下不同距离上地表质点振速峰值,并检验其反映爆破地震波随距离衰减规律的有效性和可靠性。
需要说明的是,萨氏公式的K和α是用来反映地质地形条件影响的两个参数,而等效距离公式中的K和α则是该公式的两个常数项。
4 质点振速峰值计算公式的实验检验
在一大型露天矿山进行了一系列台阶爆破震动监测,并应用最小二乘法对监测数据进行回归拟合处理,得出了公式中系统常数K和α的值。将质点振速峰值的预测值与实测值进行对比,以检验该公式的有效性和可靠性。
4.1 爆破震动监测
测振仪器为NUBOX-6016智能振动监测仪,监测记录的数据主要包括地表质点振动速度时程曲线,且可读取测点处的质点振速峰值及主频。
各测线上各个爆破振动传感器将爆破地震动信号转换为电信号,然后再由爆破震动记录仪转化为数字信号,并以如图5所示的质点振速时程曲线的形式记录保存。测点位置的质点振速峰值可由爆破震动分析软件自动从质点振速时程曲线上读出。
为保证爆破信号振动在收集阶段产生的误差尽可能减小,测点位置的岩石应较为完整且坚硬,传感器与地面间用石膏形成刚性粘结,且保证传感器水平放置,其X向指向爆心。在地表岩石破碎地段,测试时将传感器用长20cm的铁桩固定于地面,以形成传感器与地面的刚性连接,避免测得的数据失真。使用多台仪器同时测试的时候,测点分布在一条指向爆区最大一段装药量位置的直线上(见图6)。
在进行爆破震动监测的同时,系统统计爆破及最大一段起爆炸药量及其位置坐标、炮孔装药种类与爆炸性能参数、爆破振动监测传感器的位置坐标、地形与岩层数据及其他的相关爆破技术参数等。铵油炸药和乳化炸药的定容爆热QV分别为3 840、3 200kJ/kg,岩石与岩体的相关参数列于表2。监测得到的地表质点振速峰值数据列于表3。

表2 岩石与岩体的相关参数Table 2Parameters of rock and rock mass
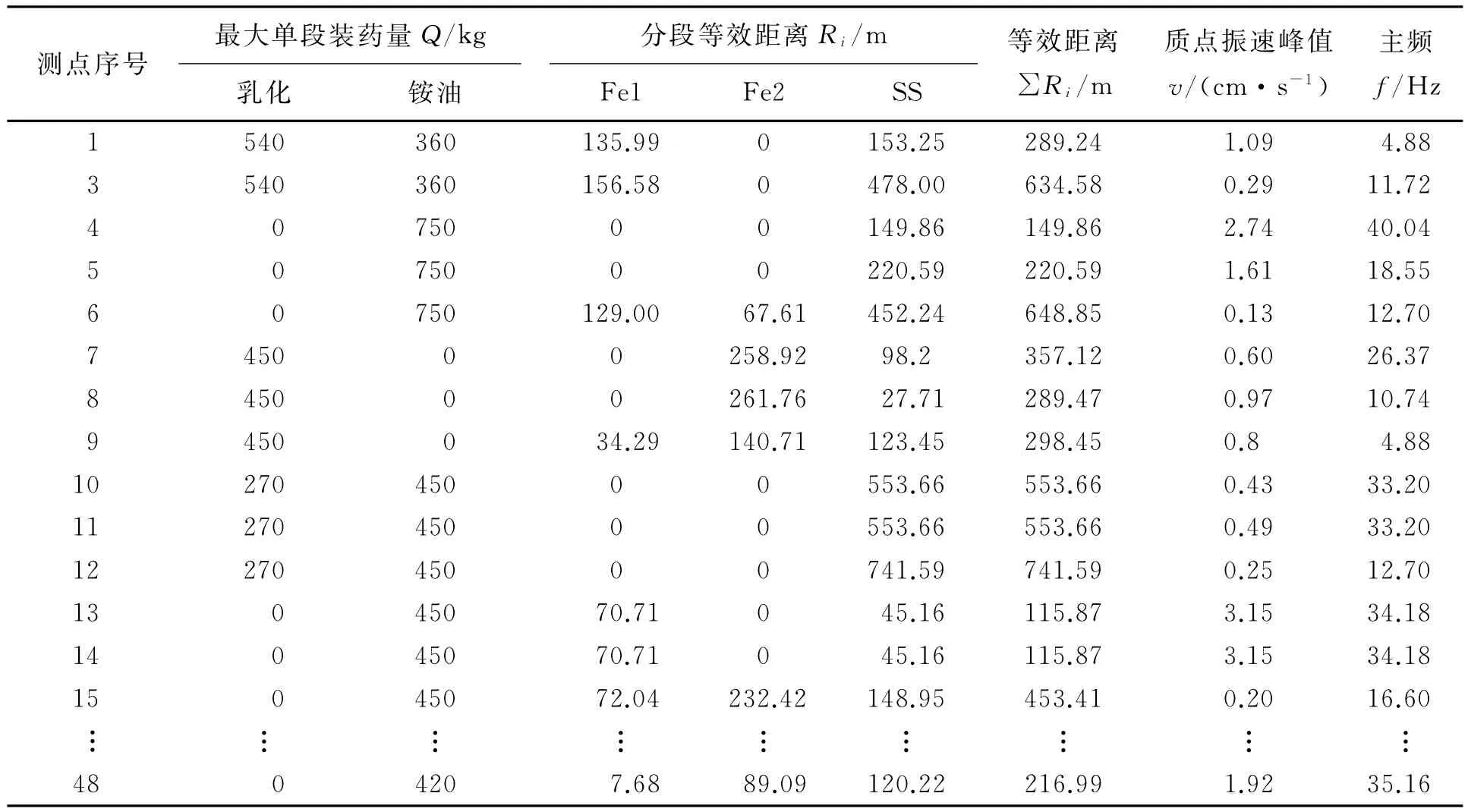
表3 质点振速峰值现场监测结果Table 3Recorded peak particle velocity(vmax)from field seismic monitoring
4.2 系统常数K、α值的求解
应用最小二乘法对表3所列质点振速峰值实测结果数据进行等效距离公式(式(4))的回归拟合分析,以求得公式常数项K、α的值,同时考察该公式与实测数据的相关性及误差水平。对式(4)两边取对数,得
按式(6)对表3所列数据进行线性回归拟合处理(图7),可得式(4)中的系统常数K=1 528,α=1.91;在置信度为95%时,其相关系数R=0.982 5,剩余均方差σR=0.226 8,质点振速峰值与式(4)等号右边的等效距离等各个参量的相关性强,且离散性较小。因此,式(4)可写为:
4.3 误差检验及结果
应用等效距离公式(式(7))对表3所列各测点的质点振速峰值进行预测,然后将预测结果分别与实测结果及应用萨氏公式预测得到结果进行对比,可以检验采用等效距离公式预测台阶爆破地表质点振速峰值的准确性和可靠性。
4.3.1 萨氏公式 K、α 值的求算
采用萨氏公式对表3所列质点振速峰值和最大一段装药量数据进行如式(5)~(6)的回归拟合处理,分别得到取水平距离和空间直线距离时萨氏公式的K和α值(见表4)。
由表4可见,用萨氏公式预测的质点振速峰值虽与最大一段装药量Q和距离R的相关性较强,但其剩余均方差都远高于等效距离公式,离散性偏大。
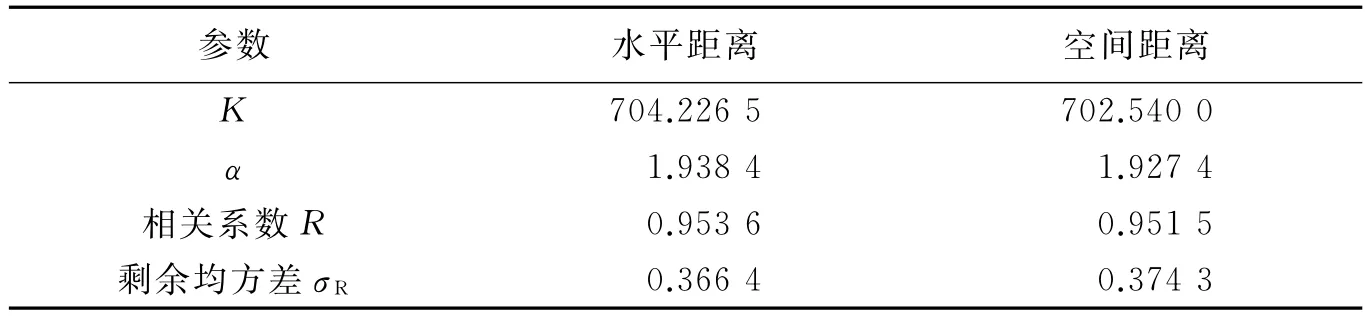
表4 萨氏公式回归分析结果Table 4Calculated results of linear regression of peak particle velocity with Sardofsky’s equation
4.3.2 预测误差计算与对比
分别应用等效距离公式和萨氏公式预测各实测位置上的爆破地震波质点振速峰值,其各自的误差分析结果如表5所示。在表5中,相对误差ε为质点振速峰值的预测值与实测值之差的绝对值与实测值之比,平均误差ε′为表5中各样本的相对误差之和与样本个数之比。

表5 等效距离公式及萨氏公式的质点振速峰值预测值与实测值的比较Table 5Relative errorεand the average relative error of the equivalent distance equation and Sardovsky’s equationto the recorded data
由表5可见:与实测值相比,采用等效距离公式预测质点振速峰值的平均误差为19.14%。而采用萨氏公式,分别取水平距离和空间距离作为公式中的距离R时,质点振速峰值预测结果的平均误差分别为32.00%和32.69%,即采用水平距离和空间距离时萨氏公式的预测误差分别比等效距离公式高约67%和71%,说明采用本文中提出的等效距离公式预测台阶爆破地表质点振速峰值,能够更准确地反映爆破地震波随距离衰减的基本规律,预测更为准确可靠。
5 结 论
(1)提出了一种预测地表质点振速峰值的计算公式——等效距离公式,该预测方法同时考虑了最大一段装药量和炸药的定容爆热、等效距离、等效路径上岩体介质的波阻抗和完整性系数等因素的影响,并且该预测公式中等效路径和等效距离概念的提出,有效反映了爆破地震波在传播路径中不同岩性和复杂地形对其衰减规律的影响。
(2)将应用该公式预测台阶爆破地震波地表质点振速峰值的结果与实测值进行对比,发现该公式能够基本准确地反映矿山环境中具体地形和地质条件对爆破地震波地表质点振速峰值的影响,预测结果的准确性显著高于国内外广泛采用的萨氏公式,表明该公式较为准确地反映了矿山复杂地形条件下爆破地震波随等效距离衰减的基本规律,为爆破震动预测提供了一种更为有效的新方法。
(3)该预测方法在台阶爆破工程中预测地表质点峰值速度的有效性和准确性已经得到验证,但在地下爆破工程预测质点峰值速度还有待进一步实践和验证。
[1] 中华人民共和国国家标准编写组.爆破安全规程:GB 6722-2014[S].北京:中国标准出版社,2014.
[2] Reza N.Prediction of ground vibration level induced by blasting at different rock units[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(6):899-908.
[3] 张继春.三峡工程基岩爆破振动特性的试验研究[J].爆炸与冲击,2001,21(2):131-137.Zhang Jichun.Vibration characteristics of blasting in bed rock mass at Sanxia Project[J].Explosion and Shock Waves,2001,21(2):131-137.
[4] 郭学彬,肖正学,张志呈.爆破振动作用的坡面效应[J].岩石力学与工程学报,2001,20(1):83-87.Guo Xuebin,Xiao Zhengxue,Zhang Zhicheng.Slope effect of blasting vibration[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(1):83-87.
[5] 朱传统,刘宏根,梅锦煜.地震波参数沿边坡坡面传播规律公式的选择[J].爆破,1988,10(2):30-31.Zhu Chuantong,Liu Honggen,Mei Jinyu.Equation selection of the transmission rule of seismic wave parameters along slope surface[J].Blasting,1988,10(2):30-31.
[6] Nguyena K V,Gatmiri B.Evaluation of seismic ground motion inducedbytopographic irregularity[J].Soil Dynamics and Earthquake Engineering,2007,27(2):183-188.
[7] 宋光明,陈寿如,史秀志,等.露天矿边坡爆破振动监测与评价方法的研究[J].有色金属(矿山部分),2000(4):24-27.Song Guangming,Chen Shouru,Shi Xiuzhi,et al.Research on the methods of measurement and evaluation of blasting vibration in open-pit mines[J].Nonferrous Metal(Mining),2000(4):24-27.
[8] Guillaume G,Picaut J,Dutilleux G,et al.Time-domain impedance equationtion for transmission line matrix modelling of outdoor sound propagation[J].Journal of Sound and Vibration,2011,330(26):6467-6481.
[9] 饶运章,汪弘.爆破振动速度衰减规律的多元线性回归分析[J].金属矿山,2013,450(12):46-47;51.Rao Yunzhang ,Wang Hong.Multiple regression linear analysis on attenuation equation of blasting vibration velocity[J].Metal Mines,2013,450(12):46-47;51.
[10] 谭文辉,璩世杰,毛市龙,等.边坡爆破振动高程效应分析[J].岩土工程学报,2010,32(4):619-623.Tan Wenhui,Qu Shijie,Mao Shilong,et al.Analysis on altitude effect ofblasting vibration in slopes[J].Chinese Journal of Geotechnical Engineering,2010,32(4):619-623.
[11] 张华,高富强,杨军,等.深凹露天爆破震动速度衰减规律实验研究.兵工学报,2010,31(增刊1):275-278.Zhang Hua,Gao Fuqiang,Yang Jun,et al.Experimental studies on blasting vibration velocity attenuation lawin deep openpit mining.Acta Armamentarii,2010,31(suppl 1):275-278.
[12] 刘美山,吴从清,张正宇.小湾水电站高边坡爆破震动安全判据试验研究[J].长江科学院院报,2007,24(1):40-43.Liu Meishan,Wu Congqing,Zhang Zhengyu.Experimentation on judging standard of blasting vibration safetyin high slope excavation of Xiaowan Hydropower Station[J].Journal of Yangtze River Scientif ic Research Institute,2007,24(1):40-43.
[13] 裴来政.金堆城露天矿高边坡爆破震动监测与分析[J].爆破,2006,23(4):82-85.Pei Laizheng.Observation and analysis of blasting vibration to the high slope of Jinduicheng open-pit mine[J].Blasting,2006,23(4):82-85.
Attenuation law of blasting induced ground vibrations based on equivalent path
Hu Xuelong1,Qu Shijie1,Jiang Wenli2,Li Hua2,Yang Wei2,Huang Hanbo2,Hu Guangqiu1
(1.Civil and Environment Engineering School,University of Science and Technology Beijing,Beijing100083,China;2.Hebei Iron and Steel Group Mining Group Company,Tangshan 063000,Hebei,China)
In this work,in view of the widely understood idea that topography and geological conditions are usually complicated and have a critical influence on the level of blast induced ground vibrations,we analyzed the effect of topography on the path through which seismic waves travel,introduced two concepts,the equivalent path and the equivalent distance,and established an equation for determining the surface peak particle velocity,taking into account of the effects of the maximum explosive charge quantity of a single initiation period,the explosion heat of the explosive product used,the acoustic impedance of the rock,and the integrity coefficient of the rock mass.A series of field seismic monitoring tests were carried out to determine the reliability of the equation.The result show that this equation can be used to describe the relationship between the peak particle velocity and the equivalent distance,and be applied under actual field topographical and geological conditions with a much higher accuracy than that of the Sardovsky’s equation,proving the reliability of the equivalent distance based equation describing the attenuation basic patterns of seismic waves and possibility for use in field practice.
blasting;ground vibration;peak particle velocity;topography;equivalent distance
O389;TD235.14 国标学科代码:13035
A
10.11883/1001-1455(2017)06-0966-10
2016-04-12;
2016-08-07
国家自然科学基金项目(51274020)
胡学龙(1989— ),男,博士研究生;通信作者:璩世杰,qushijie@ustb.edu.cn。
(责任编辑 曾月蓉)
——以徐州高层小区为例

