爆破振动诱发民房结构损伤识别的随机森林模型＊

方前程，商 丽，商拥辉，2，宋 译

爆破振动诱发民房结构损伤识别的随机森林模型＊

方前程1，商 丽1，商拥辉1，2，宋 译3

（1.黄淮学院建筑工程学院，河南 驻马店463000；2.中南大学土木工程学院，湖南 长沙410075；3.湖南科技大学能源与安全工程学院，湖南 湘潭411201）

为快速、准确地评价爆破振动诱发民房结构损伤效应，借鉴随机森林理论并结合工程实际，建立露采爆破振动诱发民房结构损伤识别的随机森林模型；综合考虑爆破参数、爆破振动特征参量及房屋结构动力特性等因素，选取质点峰值振动速度、主频率、主频率持续时间、段药量、爆心距、施工质量参数、场地条件参数、屋盖形式参数、砖墙面积率、民房高度、灰缝强度和圈梁构造柱参数等12个影响因素作为模型输入，将砖混结构建筑物的损害等级作为模型输出；基于多分类器集成的思想，以108组爆破振动实测数据作为学习样本进行训练，建模过程中由多个决策树集成随机森林、用投票的方式实现对民房结构损伤有效识别；用12组现场数据验证模型的有效性；在对样本分类的同时，计算预测变量的重要性值，发现质点峰值振动速度为最重要的评价指标，其后依次为爆心距，主频率持续时间，主频率，圈梁构造柱参数，灰缝强度，屋盖形式参数，民房高度，段药量，施工质量参数，砖墙面积率和场地条件参数。研究结果表明：随机森林模型预测结果学习样本准确度是87.97%，而测试集准确度是91.67%，与实际情况吻合较好，预测精度较高。

爆破振动；民房结构损伤；随机森林；质点峰值振动速度；预测

爆破振动产生的负面效应是矿山岩土开挖爆破难以回避的难题，尤其对近邻建构筑物的影响。而随着经济发展和我国人均生活水平的提高，人口逐渐从农村向城市转移，因此，人们对民用住房和商用建筑的需求越来越大，尤其是在繁华地段，往往建筑物的密度比较高，所以这就要求相邻的工程不能对已有的建筑物构成安全影响，因此需要建立更高的安全量化标准。

在露天开采的过程中，通常会采用爆破的方法，除了会对台阶的稳定性造成一定的影响之外；爆破产生的震动还会影响到附近的建筑物，为此，学者们力求对爆破振动诱发建筑物损害机制进行研究、对建筑物破坏机理进行分析。近些年来，国内外许多专家对爆破振动诱发民房破坏的机理进行了深入研究，从源头和传播途径上对爆破震动等级进行了预报，防止爆破振动引起建筑破坏，并划分了爆破振动等级，以上工作均取得了不错的成效。此外，国内外相继出台了一系列爆破振动安全判据、标准和规程等法律法规［1－3］，但是还没有形成一套完整的关于爆破震动诱发建筑物损害的论述体系，在实践方面缺少相关指导，项目工程方面也缺少相关数据分析。因此理论与实际往往会存在一定程度的偏差，尤其是通过观察大量的爆破工程实例后，发现某些爆破震动已经超出安全标准，却并未对周围的民房构成损害，分析其原因，一方面是因为目前的安全判据尚不完善，对于不同环境下的爆破振动诱发民房破坏可能会产生差异，而安全判据也应随之变化；另一方面是，爆破振动诱发建筑物损害程度受各种因素影响，而且诱因往往比较复杂多样，诱因和损害程度之间也呈非线性关系；因此，判别准则不具有普遍适用性。近些年来国内外一些专家通过反应谱法［4］、时程分析法［5］和波动理论分析法［6］、判别分析法［7－9］、梯度提升机［10］、模糊神经网络［11－12］和支持向量机［13］等软科学方法对其进行评估，虽然这些方法对爆破振动诱发风险评估产生了积极的影响，但是这些方法都不具有普遍适用性。具体表现在：（1）输入参量的随机性与模糊性，各参量间相互关系（包括定性与定量）尚不明晰，以及统计资料不完整性；（2）个模型型本身固有不足与局限性，如神经网络方法存在隐含层确定具有主观性，且易陷入局部最优和收敛速度慢等不足；（3）支持向量机核函数较多且难以确定合适的核函数参数等。

随机森林（random forest，RF）的算法是由 Leo Breiman和 Adele Cutler发展并推论出的［14］。作为一种包含多个决策树的分类器，随机森林算法简洁且具有较好的解释能力，近些年来被应用于自然科学和工程技术的各个领域。鉴于诱发民房破坏因素具有多样不一的特点，部分诱因难以去清晰的量化，且评价对象不是单一固定的，本文中从开挖区爆破振动对附近房屋影响的角度出发，构建露采爆破震动诱发建筑物损害的RF判别模型，以分析民房破坏等级和诱发民房破坏因素之间的关系，以便对可能产生的爆破振动进行预报，为工程操作人员提供一个可参考的依据。

1 随机森林分类原理

1.1 随机森林方法

随机森林（random forest，RF）方法本质上将隶属于集成学习范畴，其算法步骤为［14－15］：（a）在原始样本集L通过自助法（bootstrap）重采样等核心技术形成ntree个自助样本集L1，L2，…Lntree，其大小约为2L／3；（b）为自助样本训练子集分别建立分类回归决策树（CART）［15－16］，共产生ntree棵决策树形成随机森林，这些决策树生长过程中无剪枝环节，但从M 个属性中随机选择mtry（mtry≤M）个最优属性作为内部节点进行分支操作；（c）集合步骤（a）和（b）产生的ntree棵决策树预测结果，采用投票方法决定新样本归属，见图1。

1.2 RF变量重要性

RF方法相对于其他分类器的明显优势是能够识别出每个变量的重要性值，它提供了2种基本的属性重要度计算依据［14－15］：Gini importance参数和 Permutation importance参数。在随机森林节点分裂过程中，本文中采用Gini importance参数（G）来衡量各节点的样本纯度：爆破振动诱发民房结构损伤数据样本集L共有3类样本，并且每类的样本数分别是pj（j＝1，2，3），则有：

1.3 RF预测模型的评价指标

常用的精度评价方法有混淆矩阵方法，分类准确率和κ指数［16－17］。混淆矩阵是一个M×M 矩阵（M 为分类数），用于比较参照点和分类点，如表1所示。而κ指数多用于分类预测模型的精度评价，即从被评价分类比完全随机分类产生错误减少的比例角度表征模型精度，即：

式中：xii是i行i列上的值，xi＋是第i行之和，x＋i是第i列之和，N 是样本总数，r是误差矩阵行数。

根据J.Landis等的［18］建议，κ统计值与分类精度对应关系如下：κ最低允许判别精度为0.4，否则模型精度低；当κ＝0.60～0.80时，分类精度较好；当κ＝0.80～0.10时，分类效果非常好。

2 爆破振动诱发民房结构损伤预测的RF模型及其应用

2.1 确定RF模型输入输出参量

爆破振动诱发民房结构损伤主要受两方面影响一方面来自于振动源；包括段药量、装药不耦合系数、炸药的性质、起爆的方式等；另一方面取决于民房的各种参数，包括构建民房材料的性质、民房的结构、民房附近的地形条件等。除此之外，振动源与民房的距离也会影响到振动传感器的输出结果。

根据前人研究成果，并结合爆破载荷下民房结构损伤机制［7－11，13］，本模型选取爆破振动三大特征参量：质点峰值振动速度（vppv）、主频率（ν）及其持续时间（Δt），爆源因素参量：最大段药量（Qmax）和距离（R）；民房结构特征参量：如施工质量参数（Qc）、场地条件参数（Sc）、屋盖形式参数（Rs）、砖墙面积率（K）、房屋高度（H）、灰缝强度（S）和圈梁构造柱参数（Bcf）等12个主要影响民房结构损伤输入参量，其中vppv、ν、Δt、Qmax、R、S、K 和H 等参量可用实测值直接输入；对于Qc、Sc、Rs、Bcf等4个自变量和破坏等级（V）因变量均为状态参量，为了清晰度量，按照表2标准对其进行量化［7－8，10］。

表1 M 元分类问题混淆矩阵Table 1 M－ary classification confusion matrix

表2 状态参量数据量化建议值Table 2Recommended value for quantified input and output parameters

文献［7－11］中从民房结构破坏特征入手，将民房结构损伤程度分为3个类别：（1）基本完好，记为V1；（2）轻微损伤，记为V2；（3）严重破坏，记为V3，其损伤类别描述见图2，随机森林模型输出向量为V＝［V1，V2，V3］。

2.2 仿真数据采集及数据归一化处理

为验证本文中提出RF模型的有效性和可靠性，以J.Zhou等［10］和史秀志等［11］现场实测的120组建筑物采动损害实例数据作为总体样本，其中隶属于基本完好，轻微损伤和严重破坏3类民房危害类别的样本数分别为65（V1），23（V2）和32（V3），并将原始数据集随机分为2组：其中108组（编号 X1，X2，…，X108）作为RF模型训练样本集进行训练（表3），其余部分（编号C1，C2，…，C6）作为检验集（见表4）。

表3 RF模型学习样本及识别结果Table 3Training samples and identification results of RF model

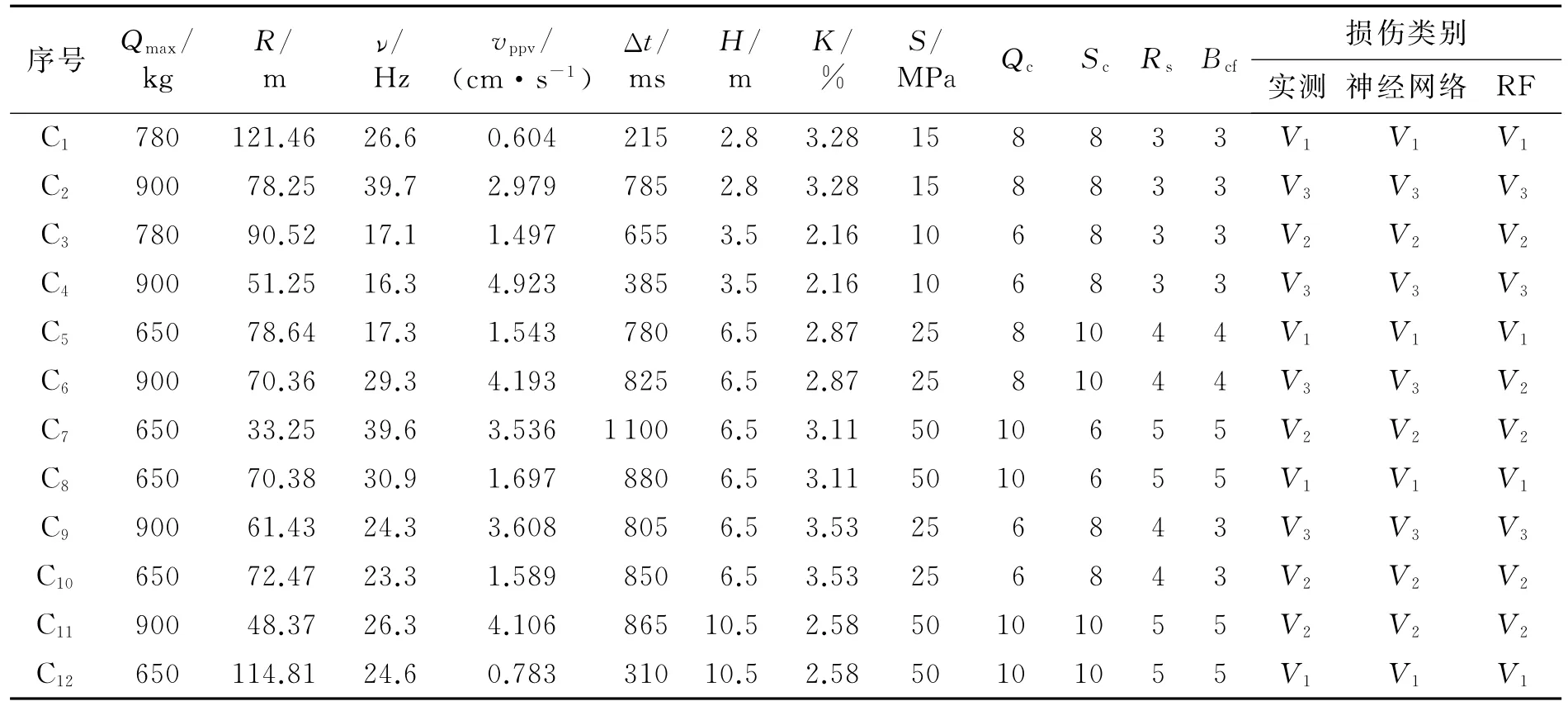
表4 RF模型测试样本及识别结果对比Table 4RF model test samples and recognition results

2.3 建立民房危害等级评估的RF模型

RF模型输入向量为（vppv，ν，Δt，Qmax，R，S，K，H，Rs，Bcf，Qc，Sc），输出层为3种损伤等级类别V：V1，V2和V3。建立映射V→F（vppv，ν，Δt，Qmax，R，S，K，H ，Rs，Bcf，Qc，Sc）。应用 RF理论，借助 R软件编制相关数据分析程序建立模型，对各个样本进行归类判别（见表4）。本文中用Random Jungle对模拟数据集生长出1 000棵树，用10折交叉验证对训练集进行遍历寻优计算，并根据最低误差选取RF模型最优参数mtry，如图3所示，在分类的过程中可生成一个泛化误差的内部无偏估计值，当mtry＝12时，该值为15.74%，10折交叉验证准确率达87.12%，κ＝0.772。RF混淆矩阵显示训练集分类误差见表5。在对样本分类的同时，利用RF模型对解释变量重要性排序，从图4可以观察到vppv为最重要的评价指标，其后依次为Bcf、R、ν、Δt、Qmax、S、Rs、H 、Qc、K 和Sc。

根据学习好的民房结构损伤识别RF模型对12个测试样本进行识别，其混淆矩阵见表6，可见识别结果与实际状态较为相符，准确率达91.67%（11／12），κ高达0.875，并与神经网络方法［11］预测结果较为一致（见表4）。从而说明构建的爆破振动诱发民房结构损伤随机森林模型泛化能力强，鲁棒性好。

与神经网络方法相比［11］，RF方法优势在于：（1）无需过多的数据预处理，RF预测精度高且运算速度高效；（2）RF可自动辨识各输入变量重要度；（3）RF受异常值和噪声的影响较小；（4）能同时处理连续型变量和分类变量。与此同时，RF缺点在于：（1）对若干数据集易呈现过拟合状态因缺少剪枝步骤；（2）对于不均衡数据集，RF算法倾向于观测值较多的类别（如V1的记录较多，而且V2和V3间的差距不大，预测值会倾向于V1）。在实际工程中，结合本文模型确定民房的损害程度，可及时对民房进行补偿或者维护，降低爆破振动带来的后续危害。另一方面为了使该模型更有说服力，可更广泛的收集爆破震动资料，建立更详细的数据库，使该方法的可信度更高。

表6 随机森林的混淆矩阵显示测试集分类误差Table 6Confusion matrix drawn from Random forest showing the classification error of test set

3 结 论

（1）综合考虑振动源的各种参数和民房的各种材料、强度性质，选取12大影响民房采动损害程度的因素（vppv，ν，Δt，Qmax，R，S，K，H，Rs，Bcf，Qc，Sc）作为 RF模型输入，将民房损害等级作为 RF模型输出，提出并建立了露采爆破振动诱发民房结构损伤的RF识别模型。（2）利用108组实测数据计算表明，利用上述指标建立的RF分析模型对爆破振动诱发民房结构损伤精度高，且方法简单实用、结果准确可靠。（3）计算预测变量的重要性值发现vppv为最重要的评价指标，其后依次为Bcf、R、ν、Δt、Qmax、S、Rs、H 、Qc、K 和Sc。

［1］ Khandelwal M，Singh T N.Evaluation of blast－induced ground vibration predictors［J］.Soil Dynamics and Earth－quake Engineering，2007，27（2）：116－125.

［2］ Siskind D E，Stagg M S，Kopp J W，et al.Structure response and damage produced by ground vibration from surface mine blasting［R］.USBM Report of Investigation 8507，1980：73－74.

i［3］ 中华人民共和国国家标准编写组.爆破安全规程：GB6722－2014［S］.北京：中国标准出版社，2015.

［4］ 史秀志，周健，崔松，等.露天采矿爆破振动对民房危害预测的DDA模型及应用［J］.中南大学学报（自然科学版），2011，42（2）：441－448.Shi Xiuzhi，Zhou Jian，Cui Song，et al.Distance discriminant analysis model and its application for prediction residential house＇s damage against blasting vibration of open pit mining［J］.Journal of Central South University（Science and Technology），2011，42（2）：441－448.

［5］ 史秀志，周健，杜坤，等.爆破振动对民房破坏效应预测的 BDA 模型及应用［J］.振动与冲击，2010，29（7）：60－65.Shi Xiuzhi，Zhou Jian，Du Kun，et al.BDA model for predicting destructive effect of blast vibration on housing［J］.Journal of Vibration and Shock，2010，29（7）：60－65.

［6］ 中国生，徐国元，熊正明.基于小波变换的爆破地震信号能量分析法的应用研究［J］.爆炸与冲击，2006，26（3）：222－227.Zhong Guosheng，Xu Guoyuan，Xiong Zhengming.Application research of the energy analysis method for blasting seismic signals based on wavelet transform［J］.Explosion and Shock Waves，2006，26（3）：222－227.

［7］ 史秀志，周健，崔松，等.露天采矿爆破振动对民房危害预测的DDA模型及应用［J］.中南大学学报（自然科学版），2011，42（2）：441－448.Shi Xiuzhi，Zhou Jian，Cui Song，et al.Distance discriminant analysis model and its application for prediction residential house’s damage against blasting vibration of open pit mining［J］.Journal of Central South University（Science and Technology），2011，42（2）：441－448.

［8］ 史秀志，周健，杜坤，等.爆破振动对民房破坏效应预测的 BDA 模型及应用［J］.振动与冲击，2010，29（7）：60－65.Shi Xiuzhi，Zhou Jian，Du Kun，et al.BDA model for predicting destructive effect of blast vibration on housing［J］.Journal of Vibration and Shock，2010，29（7）：60－65.

［9］ 董陇军，李夕兵，赵国彦，等.露天采矿爆破振动对砌体结构破坏效应预测的Fisher判别模型及应用［J］.岩石力学与工程学报，2009，28（4）：750－756.Dong Longjun，Li Xibing，Zhao Guoyan，et al.Fisher discriminant analysis model and its application to predicting destructive effect of masonry structure under blasting vibration of open－pit mine［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（4）：750－756.

［10］ Zhou J，Shi X，Li X.Utilizing gradient boosted machine for the prediction of damage to residential structures owing to blasting vibrations of open pit mining［J］.Journal of Vibration and Control，2015，22（19）.DOI：10.1177／1077546314568172.

［11］ 史秀志.爆破振动信号时频分析与爆破振动预测研究［D］.长沙：中南大学，2007.

［12］ Melih I，Mahmut Y，Hakan A.Prediction of ground vibrations resulting from the blasting operations in an openpit mine by adaptive neuro－fuzzy inference system［J］.Environmental Geology，2008，56（11）：97－107.

［13］ Shi X Z，Zhou J.Prediction residential house’s damage effect near openpit against blasting vibration based on svm with grid searching method／genetic algorithm［J］.Advanced Science Letters，2012，11（1）：238－243.

［14］ Breiman L.Random forests［J］.Machine Learning，2001，45：5－32.

［15］ 方匡南，吴见彬，朱建平等.随机森林方法研究综述［J］.统计与信息论坛，2011，26（3）：32－38.Fang Kuangnan，Wu Jianbin，Zhu Jianping，et al.A review of technologies on random forests［J］.Statistics ＆Information Forum，2011，26（3）：32－38.

［16］ 秦锋，杨波，程泽凯.分类器性能评价标准研究［J］.计算机技术与发展，2006，16（10）：85－88.Qin Feng，Yang Bo，Chen Zekai.Research on measure criteria in evaluating classification performance［J］.Computer Technology and Development，2006，16（10）：85－88.

［17］ Congalton R G.A review of assessing the accuracy of classifications of remotely sensed data［J］.Working Pages，1991，119（2）：270－279.

［18］ Landis J，Koch G.The measurement of observer agreement for categorical data［J］.Biometrics，1977，33（1）：159－174.

Random forest model for identification of residential structure damage induced by blast vibration

Fang Qiancheng1，Shang Li1，Shang Yonghui1，2，Song Yi3
（1.Institute of Architecture and Engineering，Huanghuai University，Zhumadian 463000，Henan，China；2.School of Civil Engineering，Central South University，Changsha 410075，Hunan，China；3.School of Energy and Safty Enginerring，Hunan University of Science and Technology，Xiangtan 411201，Hunan，China）

In this work，aiming to the prediction speed and accuracy，we established a random forest model for residential structure damage induced by blast vibration identification on the basis of the random forest（RF）theory.Twelve indexes，i.e.peak particle velocity，dominant frequency，dominant frequency duration，maximum charge per delay，distance，gray joints intensity，rate of brick walls，height of housing，roof structures parameter，beam－column frames parameter，quality parameter of construction and site conditions parameters，were considered as the criterion indices for this kind of damage in the proposed model based on the of analysis of the characteristic parameters of blasting vibration and dynamic characteristics of the housing structure.108sets of vibration measured data were investigated to create an RF classifier.RF was a combination of tree predictors，and variable importance was measured by gini importance parameter when the forest grows.A random tree was a combination of decision trees，and each tree is generated depending on the values of random vectors sampled independently，with the same distribution for all trees in the forest.The Gini importance value shows that the peak particle velocity is the most important discrimination indicator，followed by the distance，the dominant frequency duration，the dominant frequency，the beam－column frames parameter，the gray joints intensity，the roof structures parameter，the height of housing，the maximum charge per delay，the quality parameter of construction，the rate of brick walls and the site conditions parameters.Another twelve groups of residential structure damage instances were tested as forecast samples，and the predicted results were identical with the actual situation.Engineering practices indicate that the accuracy of the RF method of learning samples is 87.97%，and the accuracy of the test samples is 91.7%，effectively verifying and supplementing the existing methods for evaluating residential structure damage induced by blast vibration.

blasting vibration；residential structure damage；randomforest；peak particle velocity；prediction

O381 国标学科代码：13035

A

10.11883／1001－1455（2017）06－0939－07

2015－11－07；

2016－04－22

国家自然科学基金项目（11072072）

方前程（1982－ ），男，博士，fangqiancheng314＠126.com。

（责任编辑 王小飞）