基于分数阶黏弹性本构方程的井眼蠕变模型

彭瑀，赵金洲，李勇明

（油气藏地质及开发工程国家重点实验室（西南石油大学），成都 610500）

基于分数阶黏弹性本构方程的井眼蠕变模型

彭瑀，赵金洲，李勇明

（油气藏地质及开发工程国家重点实验室（西南石油大学），成都 610500）

为精确模拟井眼蠕变历程，预测和预防井壁坍塌、套管挤毁和卡钻等工程事故，在前人研究的基础上，将弹簧壶元件引入经典元件模型中，得到了分数阶模型的蠕变柔量，并验证了分数阶模型的拟合效果。研究认为分数阶模型能够实现少参数、高精度的模拟，并且相应参数的物理意义也更加明确。通过黏弹对应性原理，模拟了钻进和压井过程中的井眼蠕变情况，通过调整求导阶数可以使该模型在理想弹性体模型和标准固体模型之间转化，因此，基于标准固体本构方程和理想弹性体本构方程建立的井眼缩径模型仅是该模型的特例。分析模拟结果认为调整分数阶元件的阶数，可以在加快瞬态蠕变的同时降低稳态蠕变的速度，对蠕变曲线进行非对称调整，经典模型则无法通过调整单一参数达到这一目的，分数阶黏弹性本构方程拟合高度非线性实验数据的能力更强。图6参25

黏弹性本构方程；分数阶模型；弹簧壶元件；井眼缩径；岩石蠕变；井壁稳定性

0 引言

井眼蠕变缩径一般发生在盐膏、煤岩、泥岩和页岩等具有明显黏弹性力学特征的地层中[1-4]，会造成井壁坍塌、套管挤毁、卡钻等严重的工程事故[5-7]。岩石蠕变对煤层气、页岩气和致密油气等非常规资源开发的影响更加明显[8-9]。岩石黏弹性力学研究结果显示，蠕变模拟的核心问题是黏弹性本构方程的确定与应用[10-11]。近些年来，分数阶微积分获得了长足发展，Caputo分数阶导数定义的提出，规避了分数维初值条件无法给出的问题[12-13]，使分数阶黏弹性本构方程以物理意义明确、后期衰减速度低和拟合效果好等特点，逐渐在各种材料的黏弹性行为模拟中推广应用[14-16]。笔者在前人研究的基础上，研究了弹簧壶元件的蠕变和松弛特点，并将其引入经典黏弹性本构方程中，对比了经典和分数阶黏弹性本构方程的拟合效果，通过黏弹对应性原理，将其应用到了井眼蠕变模拟中，指导工程实践。

1 弹簧壶元件

黏弹性本构方程主要分为经验模型、机理模型和元件模型3类[17]。经验模型通过实测参数拟合得到，由于函数形式的选择比较自由，其拟合效果很好，但物理意义不明确，时间和维度的外推性能都无法得到保障；机理模型考虑损伤和微裂缝的影响，但一些参数需要人为设定，会干扰模拟结果；元件模型有比较明确的物理意义，有时间和维度外推的基础，但是对大多数的黏弹性材料而言，达到模拟精度需要的元件数量过多[18]，极大地增加了工作量。随着分数阶模型的不断发展，众多学者均认为分数阶黏弹性模型的衰减速度更低，采用较少的元件即可模拟复杂黏弹性行为[19-20]。

分数阶元件在一些文献中被称为软体元件[21]或者Abel黏壶，在此沿用文献[19]和[20]的命名，称其为弹簧壶（Springpot）。因为该元件兼有弹簧（Spring）和黏壶（Dashpot）两种元件的特性，其元件名称同样也应该具有两者的要素。

弹簧壶的本构方程为：

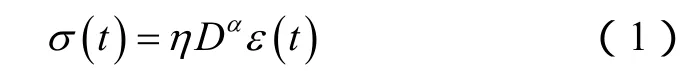
其中，分数阶导数算子采用Caputo定义[12-13]：

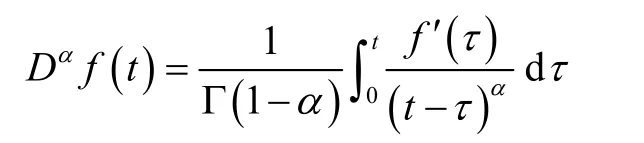
当应力一定时，可得到弹簧壶的蠕变模型：

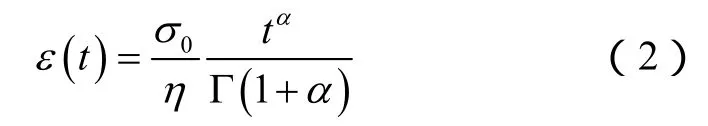
当应变一定时，可得到弹簧壶的松弛模型：

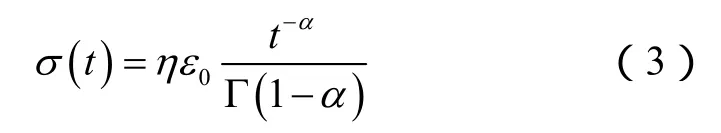
不同阶数的蠕变和松弛曲线见图1。

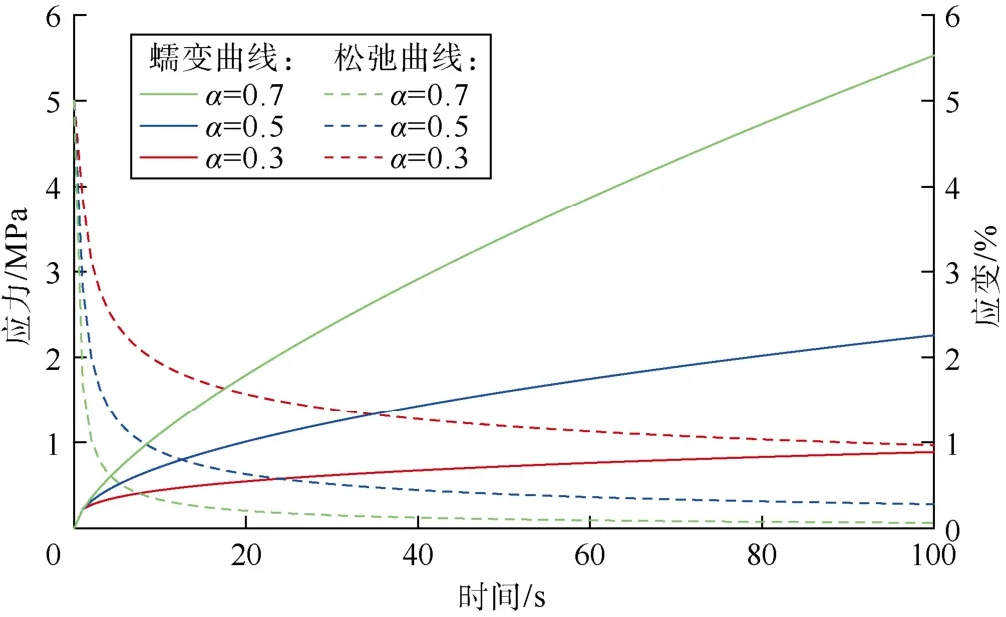
图1 不同阶数下弹簧壶的蠕变和松弛曲线

（1）—（3）式中的求导阶数α即是分数阶模型的特有参数。当α趋近于0时，模拟对象的性质更接近于理想弹性体，当α趋近于1时，模拟对象的性质逐步向黏性流体转变。当α在0～1变化时，即可模拟具有不同蠕变或松弛特征的黏弹性材料力学行为。

由图 1可见，不同阶弹簧壶元件的蠕变和松弛曲线差异很大。以求导阶数为0.5的蠕变或者松弛曲线作为分界线可以发现，低衰减速度区曲线系的稠密程度明显大于高衰减速度区。弹簧壶元件描述低速蠕变和低速松弛现象的拟合优度更高。因此，弹簧壶元件更适宜于描述岩石这一类明显偏向弹性的黏弹性材料。

2 黏弹对应性原理

在黏弹性力学中，当瞬时应力随时间变化的函数为阶跃形式时，瞬时应变（应变响应）可表示为：

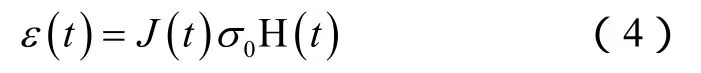
在应力变化函数比较复杂时[22]，需通过增量模型将（4）式转化成卷积形式：

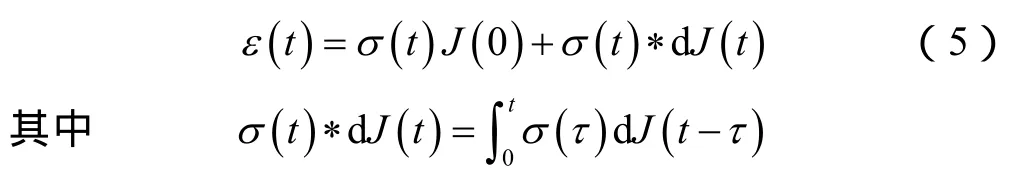
在三向应力情况下引入求和约定，采用体积模量和剪切模量表示本构方程，可得：

根据黏弹对应性原理，当边界的位置和边界条件类型不发生变化时，拉氏空间中的弹性方程组与黏弹性方程组仅在本构方程上有差异。拉氏空间中的弹性本构方程为：

拉氏空间中的黏弹性本构方程可由（6）式、（7）式得到[23]：

将（10）式、（11）式分别代入（8）式和（9）式，即可得到黏弹性问题在拉氏空间中的解：

在实际的岩石力学测试中，常用差应力和轴向应变计算弹性模量，其代换形式可由类似推导得到：

3 分数阶蠕变本构方程与实例验证

在一般的元件模型中，1个元件引入 1个待定参数，而弹簧壶元件会引入 2个待定参数。在进行不同本构方程的对比时，应该以待定参数的数量作为指标。目前，用于模拟瞬态和稳态蠕变的经典黏弹性本构模型主要有Kelvin模型，标准固体模型和Burgers模型[22]，如图2所示。

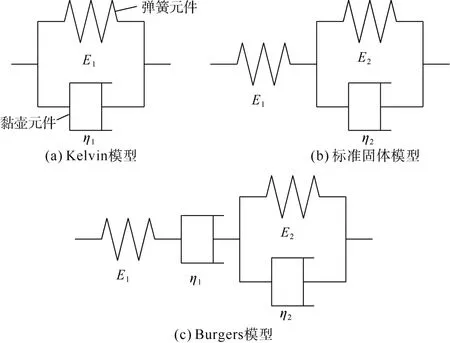
图2 经典黏弹性模型

由图2可见Kelvin模型是两参数模型，标准固体模型是三参数模型，如果将其中的黏壶换成弹簧壶，会得到三参数和四参数的分数阶模型（见图3）。

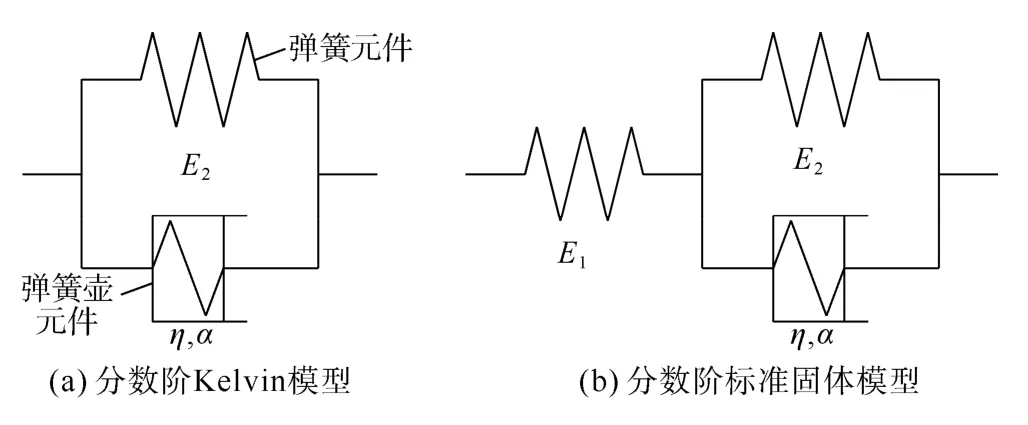
图3 分数阶黏弹性模型

图2a、图2b和图2c的蠕变柔量分别为：

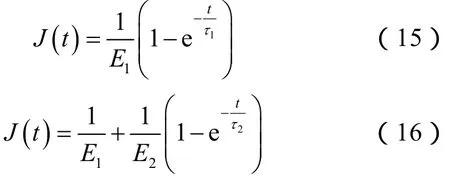
图3a和图3b的蠕变柔量分别为[24]：

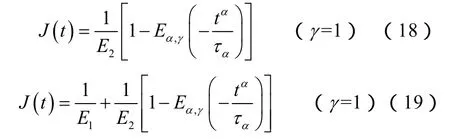
（16）式、（17）式和（19）式等号右边的第一项为弹性应变，这些模型可以模拟在 0时刻就具有弹性应变的单轴实验曲线。而（2）式、（15）式和（18）式不具有弹性部分，应减去单轴实验曲线的弹性应变再进行模拟，否则瞬态蠕变部分的拟合效果会很差。采用上述各式对文献[16]的盐岩蠕变实验数据进行了拟合，拟合的目标是使表征拟合优度的相关系数在规定的迭代次数内达到最大，拟合结果见图4。

图 4a中，Burgers模型和分数阶标准固体模型都是四参数模型，但分数阶标准固体模型的相关系数为0.997 6，大于Burgers模型的0.992 0，标准固体模型的相关系数为0.985 0，拟合优度最差。此外，分数阶标准固体模型在瞬态和稳态蠕变阶段都能很好地契合实验数据，仅在瞬态和稳态蠕变的衔接段有所偏离；而Burgers模型对瞬态蠕变的模拟不太准确。

图4b中，分数阶Kelvin模型为三参数模型，相关系数为0.997 5，拟合优度最高，而弹簧壶元件的相关系数为0.973 9，略低于Kelvin模型的0.975 4。弹簧壶元件和Kelvin模型都是两参数模型，但弹簧壶元件的相关系数更低，说明采用单一元件模拟时，分数阶元件并不具有显著优势。当弹簧壶元件与其他元件组合时，仅多引入一个参数就可以使相关系数提高到 0.99以上，超过经典四参数模型的拟合优度。

比较分数阶标准固体模型和分数阶Kelvin模型可知，两者的相关系数几乎相等，说明分数阶标准固体模型引入的弹簧元件仅代表了盐岩的弹性变形部分，只是将图4b的曲线进行了向上平移，物理意义非常明确。相比Kelvin模型，标准固体模型引入的弹簧元件使相关系数发生改变，说明弹簧元件不完全代表弹性变形。图4a中分数阶标准固体模型的截距与初始弹性变形重合，而标准固体模型和Burgers模型都发生了一定偏离，也说明在分数阶模型中引入的弹簧元件物理意义更加明确。

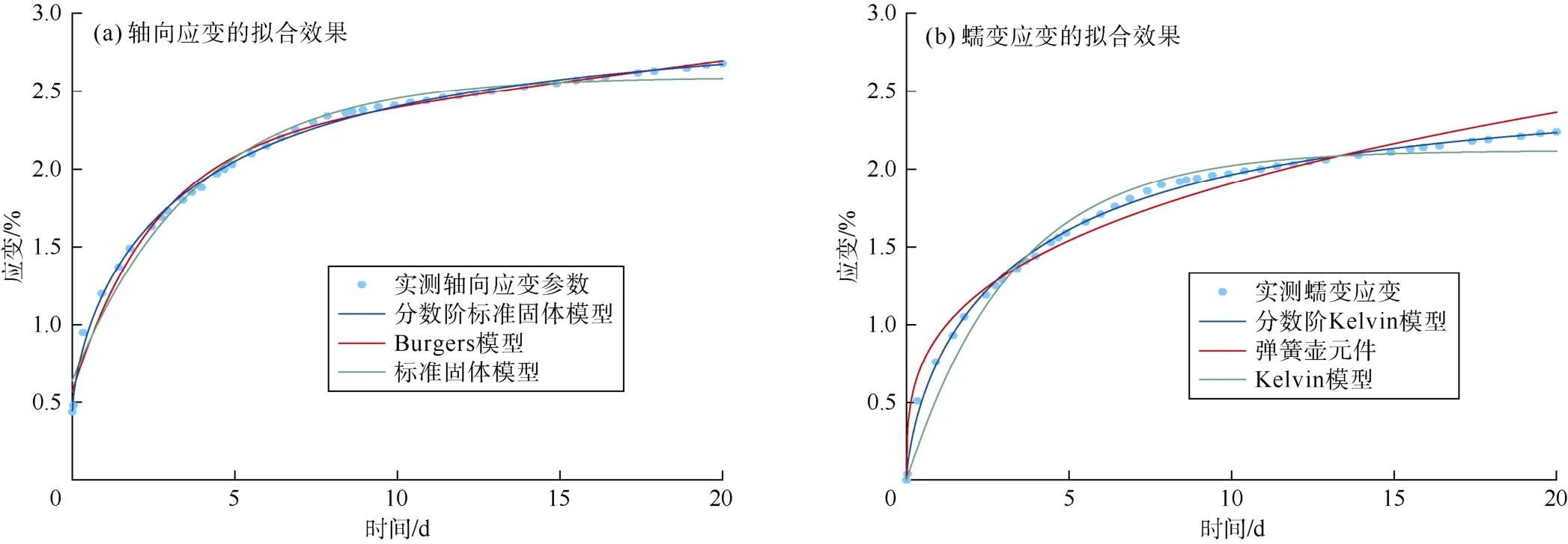
图4 分数阶和经典黏弹性本构方程对轴向应变和蠕变应变拟合效果的对比

4 分数阶井眼蠕变缩径模型

文献[25]的井周应力分布公式有一些笔误，修正后应该为：

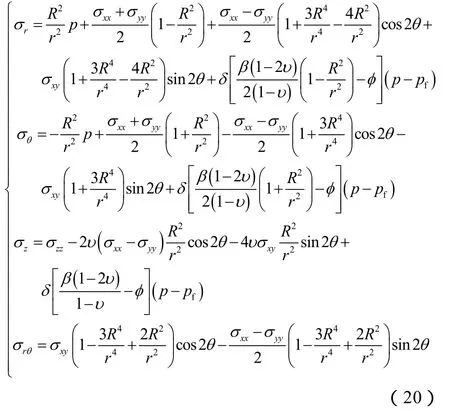
将（20）式带入正交坐标系的弹性本构方程和极坐标中的几何方程，并令r趋于无穷远处的位移为0，代入积分常数，可以得到任意位置弹性径向位移的表达式：

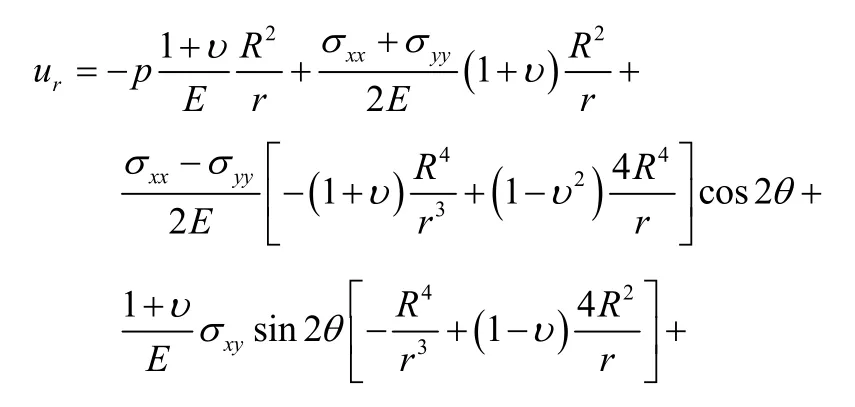
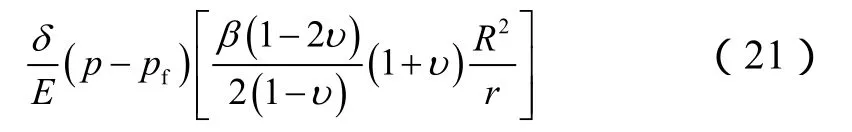
根据黏弹对应性原理，拉氏空间中弹性模量的倒数可由分数阶标准固体模型的蠕变柔量表示：

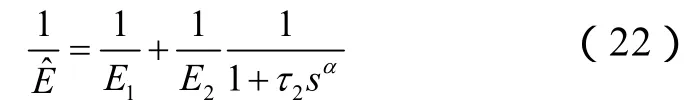
对（21）式进行拉氏变换，并将拉氏空间中的弹性模量作形如（22）式的代换后求逆变换，可得实空间中径向位移的变化：

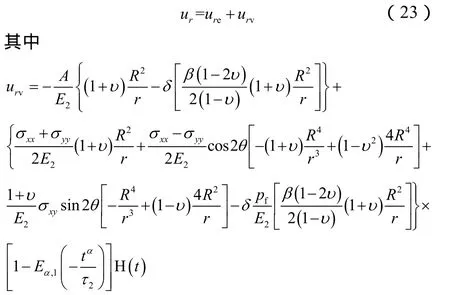
在钻进过程中一般会不断提高钻井液的密度，并在完井后将钻井液替换为密度更高的压井液，因此可将压力变化函数简化为图5所示的曲线。图5中井眼内压力变化函数为：

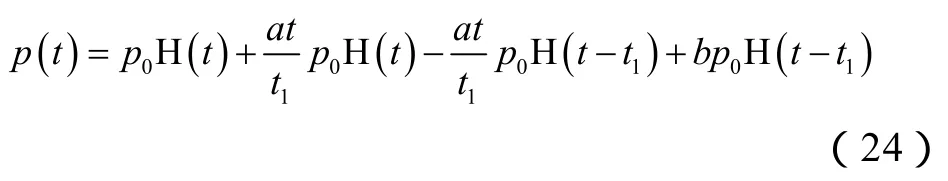
结合拉氏变换的延迟性质，与井眼内压力变化函数相关的函数A为：

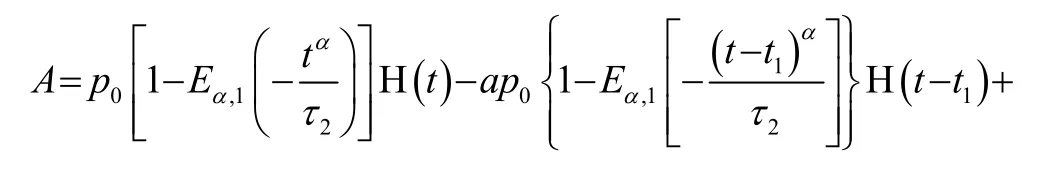
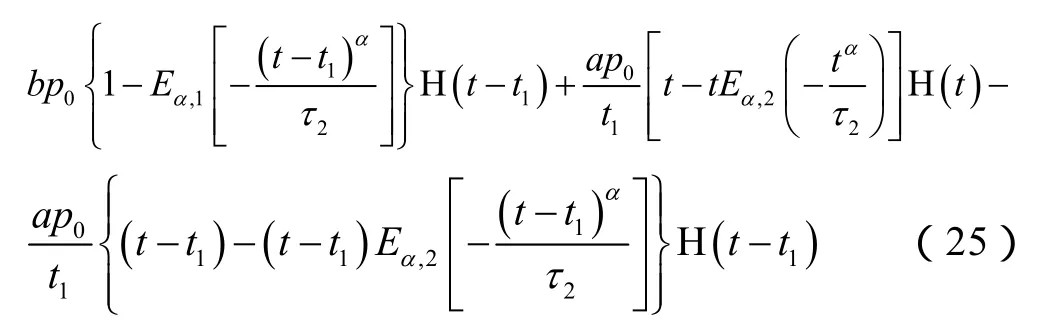
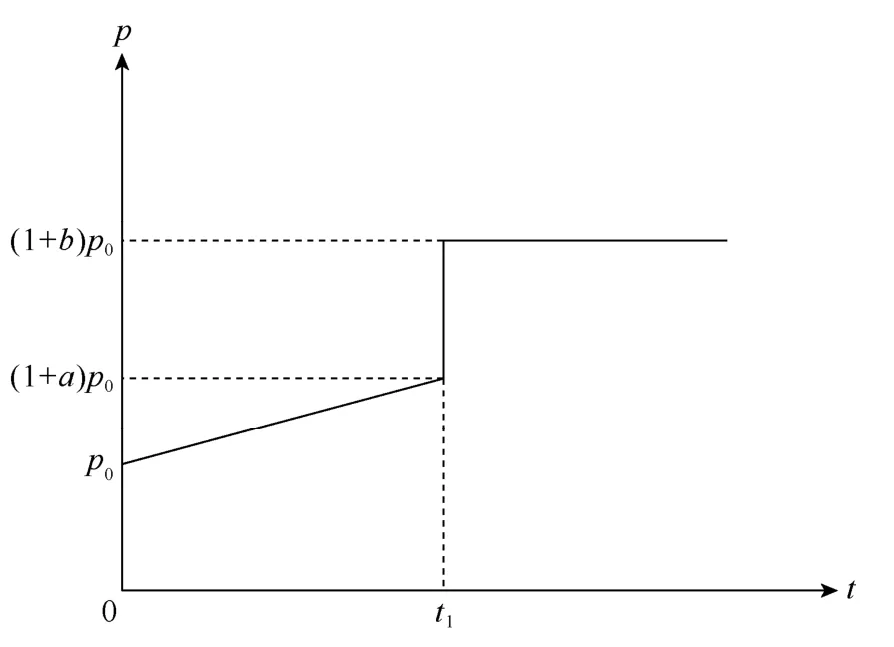
图5 井眼内压力变化曲线

针对图 5所示的井眼内压力变化曲线，模拟了钻井和压井过程中井眼的缩径情况（见图6），并对分数阶黏弹性本构方程中的参数进行了分析。

图6中在第7天出现的拐点是由于密度较低的钻井液被高密度压井液替换、井眼内压力骤然升高造成的。由于采用海维赛德函数对压力变化函数进行了处理，井眼内压力发生变化后自发地形成了蠕变恢复过程。图6a、图6b说明，井眼发生蠕变时，最危险的区域在井壁处、最大水平主应力方向。

图6c给出了求导阶数对井眼蠕变历程的影响。当α=1时，本构方程退化为标准固体模型，其衰减速度很快。刚进入压井段时，蠕变快速恢复，抵消了压井过程中的蠕变位移，井眼缩径量近似平行于横坐标。当α=0时，本构模型丧失黏性，井壁岩石成为理想弹性体，缩径量均为弹性位移，在压井段完全平行于横坐标。当α为0.25、0.50、0.75时，蠕变的衰减速度会大幅降低，压井段井壁岩石会出现长期低速蠕变的特性，与一直以来对岩石蠕变的研究成果相符。因此，基于标准固体本构方程和理想弹性体本构方程建立的井眼缩径模型仅是本文模型的特例。

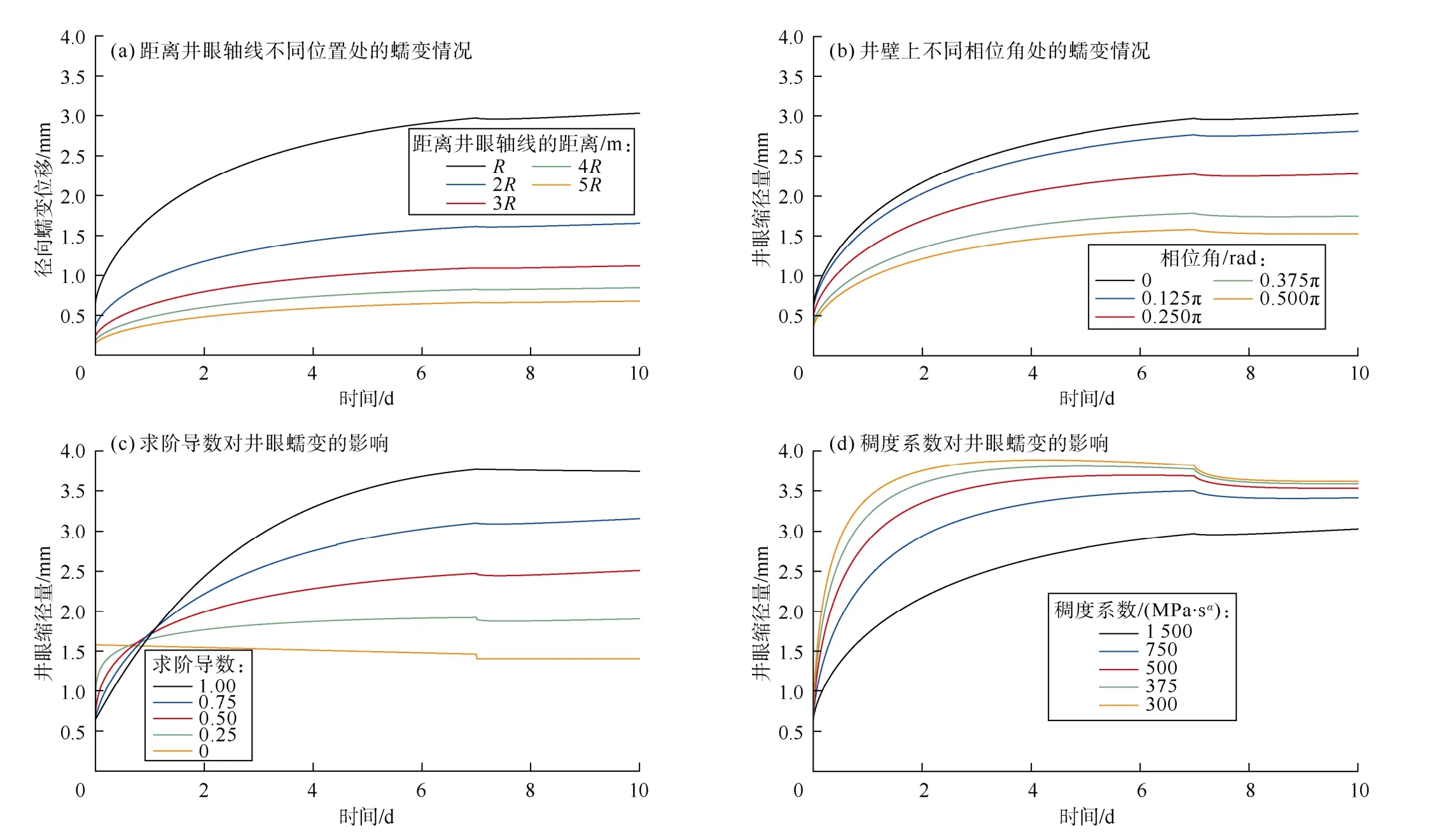
图6 分数阶井眼蠕变模型的参数分析

对比图6c和图6d可知，调整分数阶元件的阶数，可以使蠕变曲线发生旋转，在加快瞬态蠕变的同时，降低稳态蠕变的速度，对蠕变曲线进行非对称调整，经典黏弹性模型则无法通过调整单一参数达到这一目的，分数阶黏弹性本构方程拟合高度非线性实验数据的能力更强。而稠度系数对两个阶段的调整则是一致的，只能共同加强或者共同减弱。在分数阶元件的阶数和稠度系数的协同作用之下，分数阶黏弹性本构方程是一种有效的黏弹性力学分析工具。

图6d中稠度系数为300和375 MPa·sα时，井眼最大缩径量出现在替换压井液之前。这是因为井眼的缩径是由原地应力对井眼的缩径作用和内压力对井眼的扩张作用共同造成的，当岩石的瞬态蠕变大大强于稳态蠕变时，内压力在每一时刻的微小增量都会形成很强的瞬态蠕变，在原地应力对井眼的缩径作用进入稳态阶段时，整体缩径量会微弱的下降。

5 结论

分析了弹簧壶元件的蠕变和松弛模型，认为该元件更适宜于模拟岩石等蠕变速度较低的黏弹性材料。

引入双参数Mittag-Leffler函数，推导得到了分数阶Kelvin模型和分数阶标准固体模型的蠕变柔量，将其与经典模型进行了对比，发现分数阶模型的拟合优度更高，并且对应参数的物理意义更加明确。

基于分数阶标准固体本构方程和黏弹对应性原理，建立了钻进和压井过程中的井眼蠕变缩径模型，该模型中α的变化范围为0～1。模拟结果证实，基于标准固体本构方程（α=1）和理想弹性体本构方程（α=0）建立的井眼缩径模型仅是该模型的特例。

在井眼蠕变时，最危险的区域在井壁处、最大水平主应力方向；调整分数阶元件的阶数，可以在加快瞬态蠕变的同时，降低稳态蠕变的速度，对蠕变曲线进行非对称调整，经典黏弹性模型则无法通过调整单一参数达到这一目的，分数阶黏弹性本构方程拟合高度非线性实验数据的能力更强，是一种有效的黏弹性力学分析工具。

符号注释：

a，b——钻井液密度的上升幅度，无因次；A——与井眼内压力变化函数相关的待定函数，MPa；Dα——分数阶导数算子，s-α；eij——偏应变张量，无因次；eˆij——拉氏空间中的偏应变张量，无因次；E——弹性模量，MPa；E1，E2——图2、图3中对应元件的弹性模量，MPa；ˆE——拉氏空间中的弹性模量，MPa；f，f′——函数及其导数；G——剪切模量，MPa；ˆG——拉氏空间中的剪切模量，MPa；H(t)——海维赛德函数；i，j——求和约定的自由标或哑标，无因次；J(t)——蠕变柔量，MPa-1；Je——切向蠕变柔量，MPa-1；Jv——体积蠕变柔量，MPa-1；——拉氏空间中的轴向蠕变柔量，MPa-1；——拉氏空间中的切向蠕变柔量，MPa-1；——拉氏空间中的体积蠕变柔量，MPa-1；k——自然数；K——体积模量，MPa；——拉氏空间中的体积模量，MPa；p，pf——井眼内压力和地层压力，MPa；p0——钻开地层时的初始井眼内压力，MPa；r——极坐标中的极径，m；R——井眼半径，m；s——拉氏变量，无因次；Sij——偏应力张量，MPa；——拉氏空间中的偏应力张量，MPa；t——时间，s；t1——替换压井液的时刻，s；ur——径向位移，m；ure——弹性径向位移，m；urv——黏性径向位移，m；α——求导阶数，无因次；β——有效应力系数，无因次；γ——Mittag-Leffler函数的输入参数；Γ——伽马函数；δ——渗透性判别系数，当井壁有渗透时为1，井壁无渗透时为0；ε(t)——瞬时应变，无因次；ε0——初始应变，无因次；εii——应变张量，无因次；——拉氏空间中的应变张量，无因次；η——分数阶稠度系数，MPa·sα；η1，η2——图 2、图 3中对应元件的稠度系数，MPa·s；θ——极坐标中的极角，rad；σ(t)——瞬时应力，MPa；σ0——初始应力，MPa；σr，σθ，σz，σrθ——柱坐标中径向、周向和轴向的正应力以及研究平面的切应力，MPa；σxx，σyy，σzz，σxy——无穷远处直角坐标中x，y，z方向的正应力和研究平面的切应力，MPa；σii——应力张量，MPa；ii——拉氏空间中的应力张量，MPa；υ——泊松比，无因次；τ——中间变量，s；φ——孔隙度，%。

[1]赵贤正, 杨延辉, 孙粉锦, 等. 沁水盆地南部高阶煤层气成藏规律与勘探开发技术[J]. 石油勘探与开发, 2016, 43(2): 303-309.ZHAO Xianzheng, YANG Yanhui, SUN Fenjin, et al. Enrichment mechanism and exploration and development technologies of high rank coalbed methane in south Qinshui Basin, Shanxi Province[J].Petroleum Exploration and Development, 2016, 43(2): 303-309.

[2]CHANG C, ZOBACK M D. Creep in unconsolidated shale and its implication on rock physical properties[C]. San Francisco: American Rock Mechanics Association, 2008.

[3]LIU X, BIRCHWOOD R, HOOYMAN P J. A new analytical solution for wellbore creep in soft sediments and salt[C]. San Francisco:American Rock Mechanics Association, 2011.

[4]郭彤楼. 中国式页岩气关键地质问题与成藏富集主控因素[J]. 石油勘探与开发, 2016, 43(3): 317-326.GUO Tonglou. Key geological issues and main controls on accumulation and enrichment of Chinese shale gas[J]. Petroleum Exploration and Development, 2016, 43(3): 317-326.

[5]SCHOENBALL M, SAHARA D P, KOHL T. Time-dependent brittle creep as a mechanism for time-delayed wellbore failure[J].International Journal of Rock Mechanics and Mining Sciences, 2014,70(9): 400-406.

[6]吴超, 刘建华, 张东清, 等. 基于地震波阻抗的预探井随钻井壁稳定预测[J]. 石油勘探与开发, 2015, 42(3): 390-395.WU Chao, LIU Jianhua, ZHANG Dongqing, et al. A prediction of borehole stability while drilling preliminary prospecting wells based on seismic impedance[J]. Petroleum Exploration and Development,2015, 42(3): 390-395.

[7]CAO Y, DENG J, YU B, et al. Analysis of sandstone creep and wellbore instability prevention[J]. Journal of Natural Gas Science and Engineering, 2014, 19(7): 237-243.

[8]NOPOLA J R, ROBERTS L A. Time-dependent deformation of Pierre Shale as determined by long-duration creep tests[C]. Houston:American Rock Mechanics Association, 2016.

[9]MIGHANI S, TANEJA S, SONDERGELD C H, et al.Nanoindentation creep measurements on shale[C]. San Francisco:American Rock Mechanics Association, 2015.

[10]ORLIC B, BUIJZE L. Numerical modeling of wellbore closure by the creep of rock salt caprocks[C]. Minneapolis: American Rock Mechanics Association, 2014.

[11]RASSOULI F S, ZOBACK M D. A comparison of short-term and long-term creep experiments in unconventional reservoir formations[C]. Houston: American Rock Mechanics Association,2016.

[12]陈文. 力学与工程问题的分数阶导数建模[M]. 北京: 科学出版社,2010.CHEN Wen. Fractional differential modeling of the problems of mechanics and engineering[M]. Beijing: Science Press, 2010.

[13]UCHAIKIN V V. Fractional derivatives for physicists and engineers[M]. Berlin: Springer, 2013.

[14]YIN D, WU H, CHENG C, et al. Fractional order constitutive model of geomaterials under the condition of triaxial test[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2013,37(8): 961-972.

[15]PALOMARES-RUIZ J E, RODRIGUEZ-MADRIGAL M, CASTRO LUGO J G, et al. Fractional viscoelastic models applied to biomechanical constitutive equations[J]. Revista Mexicana De Física,2015, 61(4): 261-267.

[16]WU F, LIU J F, WANG J. An improved Maxwell creep model for rock based on variable-order fractional derivatives[J]. Environmental Earth Sciences, 2015, 73(11): 6965-6971.

[17]ZHOU H W, WANG C P, HAN B B, et al. A creep constitutive model for salt rock based on fractional derivatives[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1):116-121.

[18]张千贵, 梁永昌, 范翔宇, 等. 基于能量守恒定律对西原模型的改进与验证[J]. 重庆大学学报(自然科学版), 2016, 39(3): 117-124.ZHANG Qiangui, LIANG Yongchang, FAN Xiangyu, et al. A modified Nishihara model based on the law of the conservation of energy and experimental verification[J]. Journal of Chongqing University (Natural Science Edition), 2016, 39(3): 117-124.

[19]MUSTO M, ALFANO G. A fractional rate-dependent cohesive-zone model[J]. International Journal for Numerical Methods in Engineering, 2015, 103(5): 313-341.

[20]PAOLA M D, PIRROTTA A, VALENZA A. Visco-elastic behavior through fractional calculus: An easier method for best fitting experimental results[J]. Mechanics of Materials, 2011, 43(12):799-806.

[21]殷德顺, 任俊娟, 和成亮, 等. 一种新的岩土流变模型元件[J]. 岩石力学与工程学报, 2007, 26(9): 1899-1903.YIN Deshun, REN Junjuan, HE Chengliang, et al. A new rheological model element for geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1899-1903.

[22]CHRISTENSEN R M. Theory of viscoelasticity: An introduction[M].New York: Academic Press, 1982.

[23]陈德坤. 钢-混凝土组合结构的应力重分布与蠕变断裂[M]. 上海:同济大学出版社, 2006.CHEN Dekun. Stress redistribution and creep rupture of integral structure of steel and concrete[M]. Shanghai: Tongji University Press,2006.

[24]李卓. 粘弹性分数阶导数模型及其在固体发动机上的应用[D]. 北京: 清华大学, 2000.LI Zhuo. Viscoelastic fractional derivative model and its application on solid rocket motor[D]. Beijing: Tsinghua University, 2000.

[25]陈勉, 金衍, 张广清. 石油工程岩石力学[M]. 北京: 科学出版社,2008.CHEN Mian, JIN Yan, ZHANG Guangqing. Petroleum engineering rock mechanics[M]. Beijing: Science Press, 2008.

A wellbore creep model based on the fractional viscoelastic constitutive equation

PENG Yu, ZHAO Jinzhou, LI Yongming
(State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation,Southwest Petroleum University,Chengdu610500,China)

To simulate the evolution of wellbore creep accurately, predict and prevent severe accidents such as borehole wall sloughing,casing collapse and sticking of the drill, based on previous studies, the springpot element was introduced into the classical element model and the creep compliances of the fractional constitutive models were deduced. The good fitting effect of fractional constitutive model was verified. The study shows the fractional constitutive model can simulate creep with high accuracy and less input parameters, and the physical significance of the input parameters are clearer. According to the correspondence principle of viscoelastic theory, a wellbore creep model including drilling and killing processes was built up. By adjusting the value of fractional orders, the model can transform between the models of ideal elastic material and standard solid, which implies the classical wellbore shrinkage model based on standard solid model and ideal elastic model are just special cases of this model. If the fractional order is adjusted, the creep curve will change asymmetrically, which can be can be regulated by the speeding up of the transient creep and lowering the rate of steady creep, which can not be accomplished by adjusting one parameter in the classical models. The fractional constitutive model can fit complicated non-linear creep experiment data better than other models.

viscoelastic constitutive equation; fractional model; springpot element; wellbore shrinkage; rock creep; wellbore stability

国家自然科学基金重大项目（51490653）；四川省青年科技创新研究团队专项计划项目（2017TD0013）

TE21

A

1000-0747(2017)06-0982-07

10.11698/PED.2017.06.17

彭 瑀, 赵金洲, 李勇明. 基于分数阶黏弹性本构方程的井眼蠕变模型[J]. 石油勘探与开发, 2017, 44(6): 982-988.

PENG Yu, ZHAO Jinzhou, LI Yongming. A wellbore creep model based on the fractional viscoelastic constitutive equation[J].Petroleum Exploration and Development, 2017, 44(6): 982-988.

彭瑀（1988-），男，四川成都人，西南石油大学博士研究生，主要从事油气藏压裂酸化理论与应用方面的研究工作。地址：四川省成都市新都区新都大道 8号，西南石油大学石油与天然气工程学院，邮政编码：610500。E-mail: pengyu_frac@foxmail.com

联系作者简介：赵金洲（1962-），男，湖北仙桃人，博士，西南石油大学教授，主要从事油气藏压裂酸化理论与应用方面的教学和科研工作。地址：四川省成都市新都区新都大道8号，西南石油大学，邮政编码：610500。E-mail：zhaojz@swpu.edu.cn

2017-03-21

2017-09-06

（编辑 郭海莉）