独立覆盖流形法的本质边界条件施加方法

，

(1.长江科学院 材料与结构研究所，武汉 430010； 2.水利部水工程安全和病害防治工程技术研究中心，武汉 430010)

独立覆盖流形法的本质边界条件施加方法

苏海东1,2，颉志强1,2

(1.长江科学院 材料与结构研究所，武汉 430010； 2.水利部水工程安全和病害防治工程技术研究中心，武汉 430010)

2017,34(12):140-146

目前，数值流形方法、无网格法等新的数值计算方法存在本质边界条件不易严格施加的问题。针对笔者前期提出的独立覆盖流形法，通过一个悬臂梁的例子，系统地分析了本质边界条件施加问题。采用多项式覆盖函数，提出了改进边界覆盖函数和直接设定独立覆盖函数2种方法，不仅严格满足边界条件，而且能保证边界附近的近似函数逼近真实解。这2种方法避免了常用罚函数法中的罚数取值对计算结果和方程性态的影响问题，而且只需令部分自由度不参与计算就能实现，操作简单。通过设置覆盖函数来施加边界条件的方式可供其他新方法借鉴。

数值流形方法；独立覆盖；本质边界条件；多项式覆盖函数；罚函数法

1 研究背景

用有限元法[1]等数值方法求解偏微分方程的边值问题，边界条件主要包括Dirichlet边界条件和Neumann边界条件。前者指物理场在边界处的值，又称为本质边界条件，一般需要设定的近似场函数事先满足；后者指物理场在边界处的导数值，又称为自然边界条件，一般在偏微分方程的积分形式(如泛函的变分)中自然满足。

本质边界条件的施加对于有限元法而言不是问题，因为有限元法基于插值方式构造近似函数，且网格适应于边界形状，因此可以直接将边界条件施加在结点上。然而对于无网格法[2]、广义有限元法[3]、数值流形法[4]、等几何分析方法[5]等的新数值方法而言，它们或者是基于拟合方式构造近似函数，或者采用了覆盖求解域的网格(即网格与求解域的物理边界不匹配)，或者结点不同于描述边界的控制点等。因此，这些新方法在带来相对于有限元法的某些优势的同时，本质边界条件的施加反而成了需要研究的问题。目前常用的几种解决方法都有各自的缺陷[6-7]：拉格朗日乘子法增加了未知量并引入了零对角元，不能采用现有的稀疏对称正定矩阵的高效求解器；修正变分原理不再保持原函数在驻值点的极值性质而使计算精度有所降低；罚函数法的罚数取值不易确定，取值过小则约束不足，取值太大则影响方程性态；其他方法如变换法、约束方程法、与有限元耦合法，以及无网格法中特有的边界配点法、奇异权函数等，均引入了额外的复杂性。

笔者在前期提出的基于独立覆盖的数值流形方法(简称独立覆盖流形法)[8]，具有覆盖网格的任意形状、任意连接和任意加密以及自适应分析方便[9]等诸多优点。与当今大多数关于数值流形法的研究一样，该方法主要采用硬弹簧(即罚函数法)施加边界条件。本文根据独立覆盖的特性，提出独特的本质边界条件施加方法，从根本上避免罚数取值对计算结果和方程性态的影响。

2 独立覆盖流形法及其边界条件问题

图1 任意形状的独立覆盖 及其条形连接

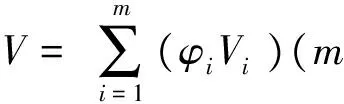
有了任意形状的覆盖后，覆盖的划分就能适应求解域的物理边界，这样，参考有限元法的方式在边界上设置边界结点就是很自然的想法，这为严格施加本质边界条件提供了方便。2015年,笔者在文献[8]中正式命名“基于独立覆盖的数值流形方法”，其中，独立覆盖和条形都是基本的计算单元(或称为覆盖网格)，但强调独立覆盖的主体作用。2016年提出梁的独立覆盖分析方法[14]，应用了适应于梁结构形状的覆盖，在边界处通过条形与施加了本质边界条件的边界结点相连，但该文限于篇幅只讨论了全约束的情况，且未说明具体的操作方法，因此本文首先对此作简要说明。

如图2(a)所示，独立覆盖①和独立覆盖②分别通过条形与边界结点相连。定义一个边界结点代表某一段边界线，从而形成独立的边界覆盖，如图中所示的1和2，它们之间通过一条短线过渡。与这些结点相关的所谓“边界覆盖”，其覆盖范围就是与之相连的所有网格(均位于条形区域)，在这些网格内仍采用有限元的线性形函数作为单位分解函数实现覆盖函数的线性过渡。在边界结点上定义覆盖函数，采用如图2(a)所示的局部坐标系x′-y′下的多项式表达式，然后根据约束的类型使某方向的自由度不参与计算(相当于这些自由度取0值)，就能分别实现法向约束、切向约束或者全约束。还可能出现如图2(b)所示的另一种情况，独立覆盖①与2个边界结点(1和2)相连，其中只有一个边界结点上带有本质边界条件。

综上所述，在引入了适应于边界轮廓的任意形状覆盖后，边界附近的独立覆盖通过条形与施加了本质边界条件的边界结点相连，独立覆盖流形法的边界条件问题似乎得到了圆满解决。然而，实际计算表明并非如此。如图3所示的单位宽度的悬臂梁，梁长l=10 m，截面高度d=1 m。在梁的自由端作用有P=2.5 kN的向下集中荷载。梁的弹性模量E=300 000 kN/m2，泊松比μ=0.2。其位移解析解为3阶多项式[15]，因此，只需用1个独立覆盖(图3中的虚线右侧区域)，覆盖函数设为3阶多项式就能逼近真实解，同时采用条形与标识为1的边界结点相连。考虑全约束，边界结点上的所有自由度均不参与计算，参与计算的独立覆盖的总体自由度数为20。

图3 一端承受集中力荷载的悬臂梁

计算结果表明：在x=0 m处的位移严格为0；当条形厚度较小时，悬臂梁的位移和应力值与解析解和材料力学解[16]很接近；然而，在条形内计算的应力值远远偏离材料力学解，且条形厚度越大，悬臂梁的位移和应力偏离解析解越大，如图4所示。

图4 采用原始方法所得的计算结果

对图3中的悬臂梁进行分析，由2个覆盖组成：一个是边界覆盖1，其覆盖范围包含结点1及条形区域，另一个覆盖2的范围是独立覆盖和条形区域。以水平向位移u为例，设覆盖2的覆盖函数u2=f(x,y)，取为3阶多项式，假设其在伽辽金法的积分方程控制下正好得到真实解。边界覆盖1的覆盖函数设为u1=0来模拟x=0 m处的全约束，那么应用单位分解函数得到条形内的位移为

(1)

从上面的简单例子可以推断，在更一般的情况下，边界附近的独立覆盖和条形不可能同时逼近真实解。因此，以上方法虽然避免了流形法通常使用硬弹簧时的弹簧系数(即罚数)的取值问题，但又在边界附近的近似函数的逼近上引入了新的问题。当然，我们可以将边界处的条形厚度取小，使之尽量不影响独立覆盖的逼近，条形处的应力也可用独立覆盖的应力表达式外推得到，然而正如文献[8]所述，过小的条形厚度影响方程组性态，其本质上相当于硬弹簧的连接，使得上述的边界条件施加方法失去实际意义，因此必须寻求新的途径。

3 边界覆盖函数改进方法

在边界附近的独立覆盖逼近真实解的同时，条形区域内的位移反而偏离真实解，其原因在于边界覆盖函数取0，使得条形内没有其他自由度，从而丧失了逼近真实解的能力。因此，解决方法就是增加自由度使之重新获得逼近能力。在条形的ξ=0处增加中结点是一种办法，也有很好的效果，但单位分解函数为有限元的二阶形函数，稍显复杂。本文尝试另一种方法，通过改进边界覆盖函数来解决问题。事实上，文献[17]也是采用了改变覆盖函数的相同思路，解决了基于单位分解的无网格法的边界条件问题。

以二维分析为例，边界覆盖的多项式覆盖函数的局部化表达式[18]为

(2)

式中：ank为待求的多项式系数；p为设定的多项式最高阶次；(x0，y0)为局部化坐标；lx和ly分别表示单元2个方向的尺度。

从式(2)可见，要使边界处的场函数为0，没有必要将边界覆盖函数所有项的系数ank都取为0，而将x0或y0取为边界坐标使某些单项式自动为0也是一种办法。本文只讨论图2所示的独立的边界覆盖形式，分为以下几种情况。

3.1 x=x0边界线上的场函数为0

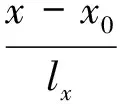
(3)

这样，其他单项式由于包含(x-x0)的幂次，则u1(x,y)在x=x0处自动为0，而在x=x0以外参与计算，使条形内的近似场函数重新获得逼近能力。

3.2 y=y0边界线上的场函数为0

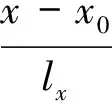
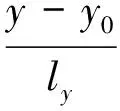
(4)

这样，其他单项式由于包含(y-y0)的幂次，则u1(x,y)在y=y0处自动为0，而在y=y0以外将参与计算。

3.3 (x0，y0)点上的场函数为0

令式(2)中的常数项为0，则有

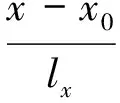
(5)

其他单项式由于包含(x-x0)或(y-y0)的幂次，则u1(x,y)在(x0，y0)点自动为0，在此之外参与计算。

重新计算图3的悬臂梁算例，边界覆盖也采用3阶多项式，参与计算的自由度总数为32。图5显示：位移与解析解、应力与材料力学解几乎重合；条形厚度不影响悬臂梁的整体位移和应力分布；但条形内的上表面应力在靠近边界处稍有偏大，存在一定的应力集中，并且随着条形厚度的减小，应力集中的程度增大，这是约束引起的正常现象，是材料力学解所不能反映的。

图5 采用边界覆盖函数改进方法得到的计算结果

为分析上述方法成立的原因,仍以图3所示的第3.1节所示情况(x=x0边界线上的场函数为0)为例，在边界结点1处，式(1)中的ξ=-1，那么u|x=x0=u1(x,y)|x=x0，因此u1(x,y)必须满足在x=x0的边界线上处处为0的条件。将x=x0代入式(2)，所有包含(x-x0)幂次的单项式都自动为0。余下的只有包含(y-y0)幂次(包括0次常数项)的单项式，即

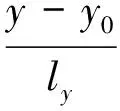
(6)

而对于边界线上任意的y值，式(6)均应为0，因此只可能有a00，a11，a22等系数为0，从而验证了第3.1节所示情况。其他情况类似。

4 独立覆盖函数设定方法

除上节的方法外，本节提出更简单的方法：去掉条形，直接设定边界处的独立覆盖函数，使之事先满足边界条件。

可以从罚函数法的角度来理解这种方法。在独立覆盖流形法中，所谓的“罚函数法”就是在包含边界的独立覆盖的边界处设置硬弹簧，强迫独立覆盖的覆盖函数满足边界条件。理论上罚数为无穷大(这同时意味着方程组的奇异)时，覆盖函数将严格满足边界条件。因此，与第3节关于式(6)的讨论一样，在3种约束情况下，此时的覆盖函数分别只能是式(3)—式(5)的形式。考虑到独立覆盖流形法的方程组是线性无关的，得到的多项式近似函数的系数只能有唯一解，那么我们可以在计算之前将x0或y0取为边界坐标，直接参照式(3)—式(5)设定独立覆盖的覆盖函数，使之事先满足相应的边界条件。

图6 采用独立覆盖函数设定方法所得的计算结果

重新计算图3的悬臂梁算例，去掉边界处的条形，只用1个独立覆盖，采用3阶多项式，事先设定其覆盖函数满足式(3)，则参与计算的自由度总数仅为12，计算结果见图6。可见，3阶多项式的位移曲线稍稍偏离解析解，升高至6阶多项式(参与计算的自由度总数为42)后与解析解基本重合。而3阶多项式的应力曲线与材料力学解完全重合，6阶多项式在固定端和加载端稍有偏离，反映出实际的约束区和荷载区对计算结果的影响，这都是材料力学解所不能反映的(位移解析解在上述区域也是有所简化的)。另外，采用罚函数法进行校核，当罚数取得非常大时(如10的20次方)，得到与上述方法几乎是同样系数的多项式，其中关于单独(y-y0)幂次项的系数非常接近于0，这也验证了本节方法与罚函数法的等价性。以此类推，上节方法也是与罚函数法等价的。

与边界覆盖函数改进方法相比，本节方法在3阶多项式情况下，由于未引入边界覆盖的自由度，因而减小了计算规模，但位移解的精度稍差。这是因为，本节方法对独立覆盖函数提出了相对较高的要求：既要在整个求解域满足偏微分方程，又要在边界上严格满足边界条件。因此，只有提高至6阶多项式时才能达到整体的收敛(此时的自由度总数反而增加)，而第3节方法的独立覆盖只需在其范围内满足偏微分方程，边界条件则由边界覆盖去满足。

考虑上述情况，将悬臂梁分为2个独立覆盖，它们之间用条形相连。其中，在距离边界1 m的范围内布置1个，采用本节方法对此独立覆盖的函数进行设定。3阶多项式情况下的自由度总数为32，图6显示，位移与解析解、应力与材料力学解的曲线几乎重合。这说明，本节方法适应于边界处的独立覆盖较小的情况，这时，覆盖内的物理场分布相对简单。

另外，当一个独立覆盖内同时有多个边界条件时，本节方法可能难以设定覆盖函数让这些边界条件同时满足，此时采用边界覆盖函数改进方法更为合适。再比如，如果独立覆盖的某段直线边界上只有一部分需要施加本质边界条件，那么本节方法也不适用，需要将此覆盖进一步分割成与边界条件相匹配的小覆盖，或者采用边界覆盖函数改进方法，如图2(b)所示，将独立覆盖与2个边界覆盖相连。

本文提出的2种方法均可应用于本质边界条件为非0常数的情况，只需在荷载向量中减去相应的刚度系数与此常数的乘积即可。另外，对于斜面约束，需要参考文献[14]引入局部坐标系下的覆盖函数表达式。

5 算 例

5.1 简支梁受均布荷载作用

文献[14]提出了梁的独立覆盖分析方法，但算例中只考虑了全约束的情况。本文增加如图7(a)所示的简支梁算例。梁长l=10 m，截面高度d=1 m，弹性模量E=300 000 kN/m2，泊松比μ=0，作用q=10 kN/m2的均布荷载。

采用1个独立覆盖，如图7(b)所示，在x=0 m和x=10 m处有2个约束，分别采用条形(宽度均取0.5 m)参照式(5)施加边界条件：在x=0 m，y=0 m处，施加2个方向的点约束；在x=10 m，y=0处施加y方向约束。

图7 简支梁受均布荷载作用

图8 受均布荷载的平板

独立覆盖和边界覆盖均采用4阶多项式。计算得到：梁中点的挠度为0.052 9 m，与材料力学解[16](0.052 1 m)很接近，它们之间的误差缘于本文考虑了剪切效应(将截面尺寸减小为0.1 m时，两者的挠度值几乎相同)；梁两端的转角为0.008 33，梁中点的表面应力为750 kN/m2，均与材料力学解[16]完全相同。

5.2 受均布荷载的二维平板

文献[19]中的一个算例，如图8(a)所示的平板，a=10 m，b=20 m，弹性模量E=300 000 kN/m2，泊松比μ=0.2。左侧和底部法向约束，右侧和顶部分别承受均布荷载，q1=20 kN/m2，q2=10 kN/m2。如图8(b)所示的流形网格，采用1个独立覆盖及1阶多项式覆盖函数，左侧和底部用条形(宽度均为0.5 m)连接边界结点，分别采用式(3)和式(4)的方式施加边界条件。注意，边界角点处(图8(a)的o点)在x和y方向也要分别采用式(3)和式(4)的方式。计算得到均匀分布的σx和σy，其数值与所施加的均布荷载完全一致，位移也与解析解[19]完全符合。

如图8(c)所示，将计算模型旋转45°，约束和荷

载情况不变。去掉条形，采用独立覆盖函数设定方法，在如图所示的局部坐标系x′-y′下，采用文献[14]提出的局部坐标系下的独立覆盖流形法公式定义约束条件。同样得到与解析解一致的计算结果。

5.3 方 孔

重新计算文献[9]的方孔算例。中部开小方孔的矩形板在上、下两端受均布拉力p=10 kN/m2。与文献[9]采用同样的1/4计算模型和网格(如图9所示)以及同样的多项式阶次设定。左边和下部采用独立覆盖函数设定方法，在边界处的独立覆盖内分别参照式(3)和式(4)施加法向约束。

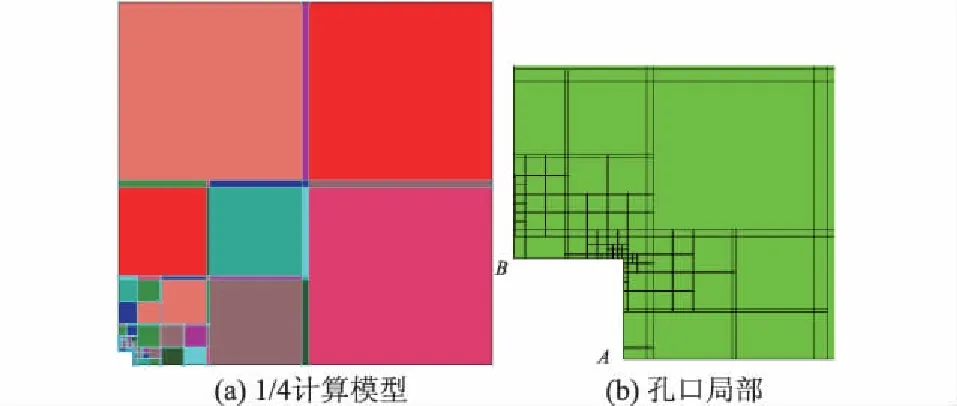
图9 方孔的1/4计算模型

采用本文方法，计算得到A点的应力为：σx=-0.02 kN/m2，σy=16.63 kN/m2(细密网格的有限元参考解为16.84 kN/m2)，τxy=0.02 kN/m2；B点应力为：σx=-8.91 kN/m2(有限元参考解为-8.90 kN/m2),σy=0.00 kN/m2，τxy=0.01 kN/m2。可见，孔口的切向应力与有限元参考解很接近，而法向应力和剪应力基本为0，满足自由面的应力条件，表明计算精度很高。

文献[9]用罚函数法施加边界条件。采用相同的方程迭代求解器[20]及同一收敛标准，当罚数取1011和109时，得到与本文相近的结果，迭代次数分别为1 170和265；罚数取107时，迭代次数为222，但A，B2点的应力误差很大。这表明罚数对计算结果有较大影响：罚数取得太小，则约束不足，误差较大；取得太大，则迭代次数明显增大，意味着方程性态的恶化和计算量的增大；而得到合适的罚数值需要一定的经验或试算。采用本文方法的迭代次数仅为233次，却可以得到稳定的计算结果。

需要说明的是，独立覆盖流形法相对于常规流形法和广义有限元法的一大优势是高阶情况下的方程组线性无关。本文方法经过以上算例的验证，当采用如图2所示的独立的边界覆盖时，方程组仍然保持线性无关的性质。

6 结 语

通过一个悬臂梁算例，系统地分析了独立覆盖流形法的本质边界条件施加问题，提出了改进边界覆盖函数和直接设定独立覆盖函数2种方法，不仅严格满足边界条件，而且能保证边界附近的近似函数逼近真实解。

本文方法等价于罚函数法中的罚数取无穷大的情况，但能够得到稳定的计算结果，没有后者的罚数取值对计算结果和方程性态的影响问题。而且无需改变独立覆盖流形法的所有特性和计算过程，只需令部分自由度不参与计算就能实现，操作也很简单。

本文方法的实现得益于独立覆盖及其覆盖函数的灵活性，即使在边界上也能根据需要选择覆盖函数使之事先满足边界条件，这与有限元法等方法通过单位分解函数在边界处为1的插值方式来施加边界条件是完全不同的路径，值得其他方法借鉴;该方法也可以推广到矩形的独立覆盖情况，在边界处增加条形或者直接设定独立覆盖函数(如第5.3节的算例)。对于采用完全重叠覆盖的常规流形法或者广义有限元法而言，也能够设置结点上的覆盖函数使之满足边界条件，但由于高阶覆盖函数情况下方程组是线性相关的(解不唯一)，或许还需验证对真实解的逼近问题。

致谢：感谢石根华博士的指导！

[1] 王勖成．有限单元法[M]．北京：清华大学出版社，2003.

[2] BELYTSCHKO T,KRONGAUZ Y,ORGAN D,etal.Meshless Methods: An Overview and Recent Developments [J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1/2/3/4):3-47.

[3] STROUBOULIS T, COPPS K, BABUSKA I. The Generalized Finite Element Method[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(32):4081-4192.

[4] SHI G H.Manifold Method of Material Analysis[C]∥U.S.Army Research Office. Transactions of the Ninth Army Conference on Applied Mathematics and Computing. Minneapolis, Minnesota, U. S. A, June 18-21,1991：51-76.

[5] HUGHES T J R，COTTRELL J A，BAZILEVS Y. Isogeometric Analysis：CAD，Finite Elements，NURBS，Exact Geometry and Mesh Refinement[J]. Computer Methods in Applied Mechanics and Engineering，2005,194(39/40/41)：4135-4195.

[6] 张 雄, 刘 岩, 马 上. 无网格法的理论及应用[M]. 力学进展, 2009, 39(1):1-36.

[7] 李录贤, 刘书静, 张慧华, 等. 广义有限元方法研究进展[J]. 应用力学学报, 2009, 26(1): 96-108.

[8] 苏海东，颉志强，龚亚琦, 等．基于独立覆盖的流形法收敛性及覆盖网格特性[J]. 长江科学院院报，2016，33(2)：131-136.

[9] 苏海东，龚亚琦，颉志强, 等. 基于矩形独立覆盖初步实现结构静力分析的自动计算[J]. 长江科学院院报，2016，33(2)：144-150.

[10] BABUSKA I, MELENK J M. The Partition of Unity Method[J]. International Journal for Numerical Methods in Engineering, 1997, 40(4):727-758.

[11] 祁勇峰, 苏海东, 崔建华．部分重叠覆盖的数值流形方法初步研究[J]. 长江科学院院报, 2013，30(1)：65-70.

[12] SU Hai-dong, QI Yong-feng, GONG Ya-qi,etal. Preliminary Research of Numerical Manifold Method Based on Partly Overlapping Rectangular Covers[C]∥DDA Commission of International Society for Rock Mechanics. Proceedings of the 11th International Conference on Analysis of Discontinuous Deformation (ICADD11). Fukuoka,Japan,August 27-29, 2013,London:Taylor & Francis Group, 2013:341-347.

[13] 苏海东, 祁勇峰, 龚亚琦, 等. 任意形状覆盖的数值流形方法初步研究[J]. 长江科学院院报, 2013, 30(12): 91-96.

[14] 苏海东, 颉志强. 梁的独立覆盖分析方法[J]. 长江科学院院报.doi:10.11988/ckyyb.20161045.

[15] 钱伟长，叶开沅. 弹性力学[M]. 北京：科学出版社，1956:213-242.

[16] 申向东，王正中．材料力学[M]．北京：中国水利水电出版社，2012.

[17] ZHENG Hong, LI Wei, DU Xiu-li. Exact Imposition of Essential Boundary Condition and Material Interface Continuity in Galerkin-based Meshless Methods[J]. International Journal for Numerical Methods in Engineering, 2017,110(4/5/6/7):637-660.

[18] 林绍忠, 祁勇峰, 苏海东．数值流形法中覆盖函数的改进形式及其应用[J]. 长江科学院院报, 2006, 23(6):55-58.

[19] 徐芝纶．弹性力学(上册)[M]．第2版. 北京：人民教育出版社，1982：361-363.

[20] 林绍忠. 用预处理共轭梯度法求解有限元方程组及程序设计[J]. 河海大学学报, 1998, 26(3): 112-115.

Application of Essential Boundary Conditions in NumericalManifold Method Based on Independent Covers

SU Hai-dong1,2, XIE Zhi-qiang1,2

(1.Material and Engineering Structure Department, Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.Research Center on Water Engineering Safety and Disaster Prevention of Ministry of Water Resources, Wuhan 430010, China)

At present, some new numerical methods such as Numerical Manifold Method (NMM) and Meshless Method are facing with the difficulty of strictly applying essential boundary conditions. Through a case study of a cantilever beam, the application of essential boundary conditions is systematically analyzed in NMM based on independent covers previously proposed by the authors. On the basis of polynomial cover functions, two methods are presented: one is the improved method of boundary cover functions; and the other is the method of setting independent cover functions. The boundary conditions are strictly satisfied, and the approximate functions near the boundaries are guaranteed to approach the real solutions. The proposed methods are refrained from the influence of penalty number in common penalty method on computational results and linear equation conditions. Moreover, the implementation is very simple, for it just needs some degrees of freedom not involved in the computation.The proposed approach of applying boundary conditions by setting cover functions has a reference value for other new methods.

Numerical Manifold Method (NMM); independent covers; essential boundary conditions; polynomial cover functions; penalty function method

2016-12-26；

2017-01-25

中央级公益性科研院所基本科研业务费项目(CKSF2015033/CL，CKSF2016022/CL)

苏海东(1968-)，男，湖北武汉人，教授级高级工程师，博士，主要从事水工结构数值分析工作和计算方法研究，(电话)027-82927167(电子信箱)suhd@mail.crsri.cn。

10.11988/ckyyb.20161345

TB115；TV311

A

1001-5485(2017)12-0140-07

(编辑：黄 玲)