自重施加方式对高拱坝廊道结构应力及配筋的影响

,,,

(1.长江科学院 材料与结构研究所，武汉 430010； 2.水利部水工程安全与病害防治工程技术研究中心，武汉 430010)

自重施加方式对高拱坝廊道结构应力及配筋的影响

陈琴1,2,龚亚琦1,2,祁勇峰1,2,颉志强1,2

(1.长江科学院 材料与结构研究所，武汉 430010； 2.水利部水工程安全与病害防治工程技术研究中心，武汉 430010)

2017,34(12):111-114，125

自重工况一般是高拱坝内廊道配筋设计的控制工况，由于高拱坝施工过程的特殊性及复杂性，有限元计算中自重有多种施加方式。结合工程实例，对高拱坝基础廊道结构进行三维有限元分析，比较不同自重施加方式对廊道结构应力及配筋的影响。研究结果表明：按整体自重考虑时，廊道结构应力及配筋面积明显偏小；全部按分缝自重考虑时，廊道结构应力及配筋面积明显大于按施工过程考虑自重的结果；为符合实际施工过程及结构承载规律，保证结构安全及经济合理，在拱坝结构的有限元计算中应按照施工过程考虑自重荷载。该研究成果对泄洪孔结构的应力分析也具有参考价值。

高拱坝；廊道结构；自重施加方式；三维有限元；配筋面积

1 研究背景

为满足灌浆、排水、观测及坝内交通的需要，高拱坝内往往布置多层廊道，廊道最小断面尺寸一般为2.0 m×2.5 m(宽×高)，最大尺寸可达4.0 m×4.5 m(宽×高),甚至更大。这些廊道削弱了拱坝结构刚度，局部改变拱坝应力，在荷载作用下，廊道周边往往会产生拉应力，需配置一定数量的钢筋保证结构安全。过去受条件限制，对于泄洪孔及廊道结构，往往采用小孔口理论[1-2]，切取若干平面进行应力分析。对于重力坝，此种方法的计算精度尚可以满足设计需要，但对于属于空间壳体结构的高拱坝，此方法已不能满足要求。随着计算机技术的发展，三维有限元法成为拱坝结构分析的主要方法之一，在对坝体内的孔洞结构进行配筋设计时，采用三维有限元法对泄洪孔结构进行精细分析的较多，而对非溢流的廊道结构进行应力分析的很少。

自重是拱坝结构的主要荷载之一，而灌浆廊道、排水廊道往往布置在坝体较低高程的位置，自重荷载对应力的影响更为明显。在以往的有限元计算中，为计算方便，结构自重的施加有2种简化方式，第1种是整体自重模式[3-6]，自重在拱坝浇筑及封拱完成后施加，按此种模式计算的应力小于实际应力，由应力计算配筋时会导致配筋不足，不利于结构安全；第2种是分缝自重模式[6-7]，偏于安全考虑，自重由各坝段独立承担，然后再封拱，按此种模式计算的结构应力大于实际应力，由应力计算的配筋量会多于实际需要，不经济。但拱坝施工是浇筑—封拱—再浇筑—再封拱的渐进过程，自重作用既不是一次性地施加于整体结构上，也不是由各坝段独立承担，以上2种自重施加方式都与按施工过程考虑自重的实际情况不符。自重施加方式对廊道结构应力及配筋的影响有多大，尚未见公开报道。

通过对某混凝土高拱坝进行有限元分析，比较不同的自重施加方式对基础廊道结构应力的影响，为配筋设计提供依据，对拱坝其他廊道及泄洪孔的应力分析也具有参考价值。

2 工程概况

某混凝土双曲拱坝，建基面高程718 m，坝顶高程988 m，坝体厚度较薄，顶部及底部拱冠处的径向宽度分别为11.98,51.4 m。水库正常蓄水位975 m，死水位945 m。坝体不设施工纵缝，采用通仓浇筑，从左岸至右岸共设置14条横缝，共计15个坝段。坝体内设置了5层纵向水平廊道，并在两岸边坡坝段通过爬坡廊道与灌浆平洞连接。基础廊道布置在5#—10#坝段，底部高程733 m，断面形式为城门洞型，尺寸为4.0 m×4.5(宽×高)，顶部拱形半径为2.0 m。

3 计算模型及计算方案

3.1 计算模型与网格剖分

有限元计算成果与网格剖分的疏密程度密切相关，为满足配筋要求，目前多采用子模型技术[3-5,7]。本文采用的计算方法类似子模型技术，即在廊道周边一定范围内细致模拟其结构形状，并划分很精细的网格，在廊道一定范围外划分较粗的网格，将局部细网格模型与整体网格粘结，施加相应荷载进行计算，程序自动耦合自由度。此种方法可以免去对子模型边界进行插值的繁琐程序，且便于分析整体变形对廊道应力的影响。

拱坝整体计算网格见图1，廊道周边局部网格见图2。共划分单元132 344个，结点149 656个。在廊道周边4 m范围内划分精细的网格，越靠近廊道表面，网格尺寸越小，最小尺寸为0.25 m。

图1 拱坝整体计算网格Fig．1 Globalfiniteelementmeshesofthearchdam图2 廊道局部网格Fig．2 Localmeshesofthecorridor

3.2 材料参数

(1) 坝体混凝土：弹性模量25 GPa，泊松比0.167，重度24.5 kN/m3。

(2) 坝基岩体：按均质各向同性弹性体考虑，左岸岩体变形模量为22.5～27.5 MPa，泊松比为0.215～0.240；右岸岩体变形模量为18.9～27.5 MPa，泊松比为0.215～0.249；河床以下岩体变形模量为27.5 GPa，泊松比为0.215。

3.3 施工过程及计算工况

施工期包含大坝上升、封拱及早期蓄水的过程。本文主要比较自重的影响，因此只考虑加高及封拱过程，施工过程及对应的计算工况如表1所示。工况7-1、工况9-1及工况10-1只有封拱过程，未增加新的荷载。

3.4 计算方案

根据自重的施加方式，拟定4种计算方案。

(1) 方案1：自重在拱坝施工封拱完成后施加，即整体自重。

表1 施工过程及施工期计算工况

(2) 方案2：自重由各坝段独立承担，即分缝自重。

(3) 方案3：分2段考虑分缝自重，高程828 m以下坝体自重为分缝自重，由各坝段独立承担，再封拱至795 m，浇筑高程828～988 m段坝体，该段坝体自重由高程795 m以上的独立坝段及高程795 m以下联成整体的坝体共同承担。

(4) 方案4：自重按表1所示的浇筑、封拱过程计算(只考虑自重的影响，不考虑蓄水的作用)。

对于考虑施工过程的计算方案，每一步施加增量荷载，然后对各工况进行叠加。

4 成果分析

按照配筋要求，应力及配筋按顶部环向、顶部轴向、底部垂直轴向、底部轴向整理，应力方向示意图见图3。

图3 应力方向示意图

4.1 应力比较

(1) 自重作用下，顶部及底部一定区域产生拉应力，表面最大，工况8-1情况下的拉应力最大。同一计算方案中，5#及10#坝段靠近陡坡坝段，由于侧向基岩的支撑作用，拉应力较其他坝段小，6#—9#坝段位于河床中部，应力比较接近。同一坝段，廊道顶部环向及底部垂直轴向应力大于轴向应力。

(2) 同一坝段的廊道应力，各计算方案应力分布规律相同。顶部表面环向及轴向拉应力主要集中在对称轴附近2 m范围内；底部表面，除侧墙根部外，其他区域基本都为拉应力。顶部环向及底部垂直轴向，拉应力大但沿高度方向衰减快，如7#坝段，沿高度方向的受拉区长度分别为0.7 m及1.0 m；顶部轴向及底部轴向，拉应力值相对较小但沿高度方向的受拉区长度大，7#坝段沿高度方向的受拉区长度分别为1.8 m(方案1)、3.5 m(方案2)、2.5 m(方案3)、2.5 m(方案4)。由于拱坝体形的影响，应力沿廊道中心轴线并不完全对称。7#坝段廊道在方案4情况下的顶部及底部表面应力等值线见图4。

图4 7#坝段廊道顶部和底部表面应力等值线(方案4)

(3) 不同计算方案的应力值差别较大。以7#坝段的廊道应力为例，不同自重施加方式下的廊道顶部及底部表面拉应力最大值(非应力集中点处)比较见表2，沿1-1剖面的应力分布比较见图5，其中顶部沿环向展开，即图5(a)中横坐标所示距离为弧线距离。

由表2及图5可见，按整体自重计算的方案1的应力最小，按分缝自重考虑的方案2的应力最大，方案1、方案2的应力与方案4的应力均差别较大，方案3的应力与方案4相对接近。如7#坝段，方案1至方案4拱顶环向应力最大值分别为1.77，3.98，3.49，2.89 MPa，拱顶轴向应力最大值为0.67，1.78，1.35，1.19 MPa。与考虑施工过程的方案4比较，各方案与方案4的应力比值分别为0.56～0.62(方案1)，1.35～1.56(方案2)，1.11～1.21(方案3)。

表2 拉应力最大值比较(非应力集中处)

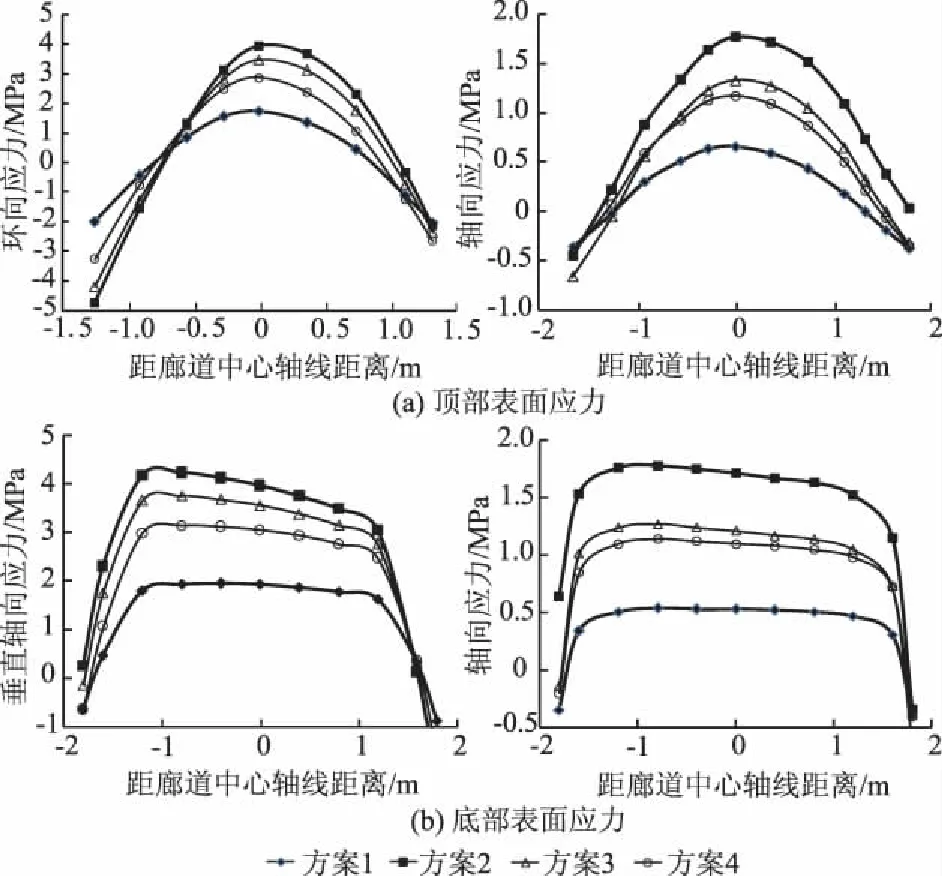
图5 7#坝段廊道1-1剖面顶部和底部表面应力比较

(4) 5#坝段的应力最小，方案1至方案4顶部环向应力分别为0.86，2.40，1.93，1.67 MPa，底部垂直轴向应力最大为1.41，2.90，2.42，2.11 MPa。

4.2 配筋面积比较

廊道结构为非杆件体系结构，不宜按照杆件结构力学方法配筋，根据《水工混凝土结构设计规范》(DL/T 5057—2009)[8]规定，由弹性力学分析方法求得结构在弹性状态下的截面应力图形，再根据拉应力图形面积，确定承载力所要求的配筋数量。

在水荷载作用下，廊道周边产生压应力，施工期的自重工况8-1为控制工况。7#坝段的廊道拉力和配筋比较见表3，表中拉力为按标准荷载计算，从偏于安全考虑，不计混凝土承担的拉力，配筋面积统一考虑各分项系数的影响，分项系数参照规范[8]取值，钢筋抗拉强度设计值取360 N/mm2。

表3 7#坝段廊道拉力和配筋面积比较(最大值)

由表3可知，对于各向拉力及所需配筋面积，各方案差别较大。同一坝段均为方案1最小;方案2最大;方案3分2段考虑自重作用，结果与方案4相对比较接近。如7#坝段，方案1的配筋面积均小于3 200 mm2/m；方案2除顶部环向外，配筋面积都在7 150 mm2/m以上；方案3、方案4在底部垂直轴向所需配筋面积最大，分别为6 126.3，5 098.6 mm2/m。

与按施工过程考虑自重的方案4比较，方案1至方案3顶部环向及底部垂直廊道轴向所需配筋面积与方案4的比值分别为0.56～0.62，1.41～1.57，1.20～1.26，顶部及底部轴向拉力与所需配筋面积与方案4的比值分别为0.40～0.43，2.02～2.05，1.05～1.06。

5 讨 论

(1) 按整体自重计算的应力偏小，为按施工过程考虑自重的60%，最大拉应力仅为1.96 MPa，小于C35混凝土的抗拉强度标准值2.20 MPa，容易造成开裂风险低的假象，总体所需配筋面积也仅为按施工过程考虑的50%。按此种方式计算结果进行配筋设计，配筋量会偏少，结构安全得不到保证。

(2) 按分缝自重计算的应力偏大，总体为按施工过程考虑的145%，最大拉应力为4.23 MPa，远超C35混凝土的抗拉强度标准值，开裂风险很大。按此种方式的计算结果配筋，总体所需配筋面积为按施工过程考虑的176%左右，不经济。

(3) 按施工过程考虑自重时，与实际情况相符，廊道最大拉应力为2.89 MPa，也存在一定的开裂风险，但由于沿高度方向的受拉区很小，开裂深度不会很大。本文只粗略考虑了施工过程，在有条件的情况下，可以对施工过程进行更细致的模拟。

6 结 论

(1) 对于高拱坝内的廊道结构，按整体自重考虑及按分缝自重考虑，所得廊道应力及配筋面积与按施工过程考虑的结果有差异，为符合实际施工过程及结构承载规律、保证结构安全及经济合理，对于自重荷载，应考虑施工过程，并按相应计算结果进行配筋计算。

(2) 施工期的自重工况一般是廊道结构配筋计算的控制工况，本文重在比较不同自重施加方式对高拱坝内廊道结构应力及配筋的影响，因此文中只考虑了自重作用，在实际的配筋计算中，除了按施工过程考虑自重作用外，还应考虑施工过程中的蓄水过程及运行期的温度荷载作用。

(3) 在高拱坝内，受布置的影响，廊道与泵房及集水井、电梯井等孔洞往往距离很近，各主要廊道间会通过交通廊道连接，这些都会对相邻的廊道结构应力产生影响，因此，在计算中也应考虑这些孔洞的影响。

本文对基础廊道结构作了分析比较，其研究成果对泄洪孔等结构的受力分析也具有参考价值。

[1] 潘家铮. 重力坝的设计和计算[M].北京：中国工业出版社，1965.

[2] 陈 进，黄 薇，丁 茜. 大坝矩形孔口应力状态分析[J]. 水力发电，2000,(12):21-24.

[3]车 轶， 宋玉普. 混凝土高拱坝孔口三维非线性分析[J]. 大连理工大学学报，2003,43(2):218-221.

[4] 李守义，杨胜梅，高菊梅. 拱坝泄水孔应力影响因素分析[J]. 应用基础与工程科学学报，2010，18(1)：20-26.

[5] 王新伟，孙文颖，史长莹，等. 拱坝坝体及孔口应力有限元仿真分析[J]. 水科学与工程技术，2010,(4):23-25.

[6] 郭胜山，翟恩地，李德玉，等.分缝自重与整体自重对乌东德拱坝动力横缝张开度的影响[J]. 水电能源科学，2010，34(8)：79-82.

[7] 陈 琴.构皮滩水电站拱坝孔口及闸墩结构三维有限元分析[R]. 武汉：长江科学院，2010.

[8] DL/T 5057—2009，水工混凝土结构设计规范[S]. 北京：中国电力出版社，2009.

Influence of the Way of Applying Gravity on Stress andReinforcement of Corridor in High Arch Dam

CHEN Qin1,2，GONG Ya-qi1,2，QI Yong-feng1,2，XIE Zhi-qiang1,2

(1.Material and Engineering Structure Department, Yangtze River Scientific Research Institute, Wuhan 430010, China; 2.Research Center on Water Engineering Safety and Disaster Prevention of Ministry of Water Resources, Wuhan 430010, China)

Gravity load case is generally the control condition of the reinforcement design of high arch dam. Because of the particularity and complexity of the construction process of high arch dam, there are several ways to apply gravity load, such as joint deadweight and whole deadweight. In this paper, the influence of gravity applying approach on corridor stress and reinforcement of high arch dam is studied through three-dimensional finite element analysis. Results show that in whole deadweight case, the stress and reinforcement area of the corridor structure are apparently small; while in joint deadweight case, the stress and reinforcement area of the corridor structure of are obviously larger than those of the deadweight results according to construction process. According to the actual construction process and the bearing capacity law of the structure, gravity load should be considered in the construction process in finite element calculation of arch dam to ensure structural safety and economic rationality. The research achievements could be taken as reference for the design of overflow outlet structure.

high arch dam；corridor structure；way of applying gravity；3-D finite element; reinforcement area

2017-04-14；

2017-06-17

中央级公益性科研院所基本科研业务费项目(CKSF2016022/CL，CKSF2017040/CL)

陈 琴(1971-)，女，湖北钟祥人，高级工程师，硕士，主要从事水工结构数值分析工作，(电话)027-82829754(电子信箱)chenqin8317@163.com。

10.11988/ckyyb.20170408

TV314

A

1001-5485(2017)12-0111-04

(编辑：黄 玲)