低相关性压缩感知表示基学习算法

杨颖颖

（滁州职业技术学院 基础部，安徽 滁州 239000）

低相关性压缩感知表示基学习算法

杨颖颖

（滁州职业技术学院 基础部，安徽 滁州 239000）

压缩感知理论作为一种新的信息压缩与采样理论，广泛用于各种信号的压缩与采样.提出一种低相关压缩感知稀疏表示基学习算法，用于实现稀疏投影下的自适应稀疏表示基设计，从而有效提高在稀疏采样压缩情况下的压缩感知数据信号的恢复性能.实验结果表明本文提出的方法可以有效提高数据恢复性能.

压缩感知；表示基学习；低相关性；投影矩阵

0 引言

压缩感知（Compressive sensing，CS）理论作为一种新的信息获取与采样技术，其认为只要对稀疏信号进行少量的线性组合即可恢复被采样的稀疏信号［1］.近年来，压缩感知理论已被国内外学者进行大量研究，同时被广泛用于图像压缩、去噪、降维、数据收集等众多应用领域［2-5］.然而，传统的压缩感知理论主要集中在两个方面：其一是在给定投影矩阵情况下，如何减少采样值数目.通常假设投影矩阵为高斯随机投影矩阵.其二是在稀疏信号的恢复算法上，通常假设带压缩信号在通用正交稀疏表示基是稀疏的，如DFT表示基、DCT表示基、DWT表示基等［1］.但在很多实际应用中，投影矩阵要求每行只有一个非零元素，则通用的稀疏表示基很难满足压缩感知理论的要求，能精确恢复被采样数据［3-4］.

针对稀疏投影矩阵下的信号采样与恢复，本文提出一种低相关性压缩感知表示基学习算法，进行稀疏投影下自适应稀疏字典学习，以实现对数据的有效稀疏采样与精确恢复.本算法是利用压缩感知中投影矩阵与稀疏表示基需要满足低相关性要求，并结合历史数据进行稀疏表示基的自适应学习.

1 问题描述

1.1 压缩感知

假设X为一个长度为N的信号，如果‖X‖0＜＜N，则向量X称为稀疏的，那么可以通过X的M个随机线性组合值来重构X.假设X的线性变换矩阵为ΦM×N，则yM×1=ΦX，其中M＜N，Φ称作测量矩阵.换句话说，如果X足够稀疏，我们可以从y中恢复信号X.通常情况下X并不稀疏，但X可以在另一个变换域下稀疏表示.例如，X=ΨN×NSN×1，S是一个系数向量且‖S‖0=K(K＜＜N).矩阵Ψ作为表示基，则测量向量表示为：

由于方程数M远小于变量数N，故这是一个欠定线性方程组，寻找这个问题的解决方案是近年来广泛研究的课题.目前主要有如下大致几类解决方案.第一类是寻找最小l0范数：

直接解决上述问题是棘手的，但目前最快速的方法是平滑的l0范数.第二类方法绕过原始的l0范数，

式

（3）用LP（linear programming）方法可以很容易解决.除了LP算法，还有IRWLS（Iterative Re-weighted Least Squares），OMP（OrthogonalMatching Pursuit），这些算法计算比LP快，但评估质量要比LP低，尤其在信号不足够稀疏时.

使用上面任何的恢复算法，K稀疏的信号都可以从M个测量值中高精度恢复，只要M满足如下条件：

其中，C是常数，N是信号维度，u(Φ,Ψ)是矩阵Φ和矩阵Ψ的相关性.假设给出一对RN的正交基(Φ,Ψ)，u(Φ,Ψ)可以定义为：

而是寻找解决最小l1范数问题来降低计算复杂度，被称为BP（Basic Pursuit）：

其中，ϕi和ψj分别是Φ和Ψ的行和列.对于给定的Φ和X，Ψ，必须满足以下两点：1）X必须在Ψ域上稀疏；2）Ψ必须使得u(Φ,Ψ)尽可能小.

1.2 字典学习

字典学习是一种常见的稀疏表示基提取方式［7］.假设给定字典，字典D中每列数据dk∈Rn称为一个原子，则信号可以用字典D中若干相关原子进行线性相关表示，即X=DA.其中，是信号X在字典D下的表示系数. 如果αi中仅有S(S＜＜K)个非零系数，我们就称系数αi是S-稀疏的.综合模型一般情况下使用l0或者l1范数来衡量表示系数的稀疏性.字典D的学习过程如下：

1.3 问题建模

由压缩感知理论可知，待收集信号X本身通常并不稀疏，但X在某个稀疏变换域上是稀疏的，如X=Ψ⋅S，其中Ψ为稀疏表示基，S为变换后的信号，并且S只有K个是非零值.对信号稀疏表示的意义在于：只有稀疏信号才能在测量矩阵的观测下精确重构数据，因为稀疏信号中“零”值元素很多，因此在信号重构时数据不会失真.

近几年来，除了基于稀疏表示基的稀疏表示技术外，基于冗余字典的稀疏分解已经吸引研究学者们的广泛兴趣.这是一种新颖的信号稀疏理论：冗余字典使用超完备的冗余函数库代替基函数，字典中的一列数据称为一个原子.对一个稀疏表示基的学习我们采用字典学习的方法.用一组数据作为学习字典的训练数据，其中xi∈RN是一个N维数据向量.用矩阵X∈RN×L作为训练数据：

稀疏表示基学习的一般形式为

其中，‖·‖F为矩阵的范德蒙范数；S为稀疏信号的稀疏度，C∈RK×L为稀疏信号矩阵.将作为互相干性惩罚项（提高信号的重构精度）加入到式（8）中，得到一个优化稀疏表示基的学习模型：

通过求解优化模型式（9），则可以得到稀疏表示基.

2 问题迭代求解

为求解优化问题式（9），提出交替迭代算法，在每次循环迭代优化过程中主要包含以下两个步骤：①稀疏求解；②表示基更新.

2.1 稀疏求解

在稀疏求解阶段，首先固定稀疏表示基Ψ，然后求解训练数据X在稀疏表示基Ψ上的稀疏表示矩阵C，求解公式如下

对于式（10）采用OMP算法来求解.

2.2 表示基更新

在更新阶段，首先固定稀疏矩阵C，根据下面的优化模型求解出新的表示基Ψ：

发现式（11）是一个凸优化问题，必定存在一个全局最优解.令

对g(Ψ)进行求导可得：

令g′(Ψ)=0 ，得到

用式（13）作为优化模型（11）的最优解的近似估计，在迭代过程中对表示基进行更新：

其中，Ψk+1是第k+1轮循环中更新的稀疏表示基；ψk是第k轮循环中更新的稀疏表示基.每次得到更新表示基都要对每一列进行单位化处理.综合上面所述，交替迭代求解稀疏表示基的算法执行流程如图1所示.

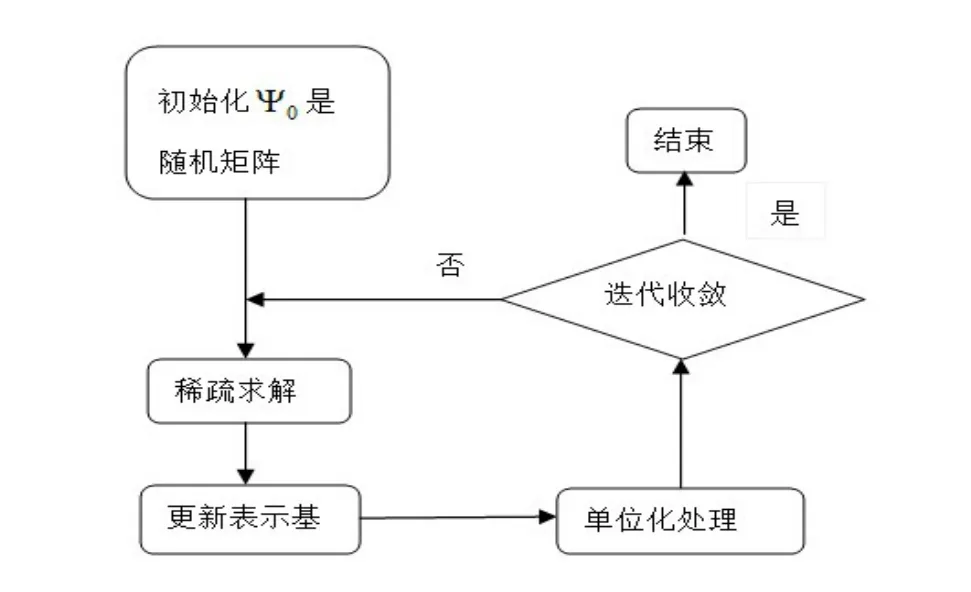
图1 交替迭代算法流程

3 实验

3.1 实验方案

为了验证本文算法的有效性，采用灰度图像数据进行模拟实验.实验图像如图2和图3所示，这两个实验图像大小都是1024*1024.

本文将两幅图像分割为1024*128和1024*896两个部分，1024*128作为训练数据，1024*896作为测试数据.整个实验过程主要分为以下两个步骤：首先是运用本文的算法对图像矩阵进行字典学习并得到稀疏表示基；然后观测该稀疏表示基在测试数据集上的稀疏表示能力.为了充分验证本文的稀疏表示基学习算法的效果，故选择固定的DCT［10］字典和 K-SVD［6-7，9］算法学习的字典进行对比 .

图2 模拟数据1

图3 模拟数据2

3.2 实验结果

从训练数据集得到稀疏表示基D后，评测该表示基在测试数据上的稀疏表示能力.首先得到测试数据集X在稀疏表示基上的稀疏表达：

则稀疏表示的误差用式（15）表示：

图4显示本文的表示基学习算法、DCT字典、k-SVD在（a）模拟数据集1和（b）模拟数据集2上的稀疏表示能力.

图4 不同表示基的稀疏表示能力

4 总结

本文通过对低相关性压缩感知表示基学习算法展开研究，提出一种基于历史数据的稀疏表示基学习方法，从而有效提高稀疏投影下压缩感知数据恢复性能.实验结果表明本文提出的方法比传统通用稀疏表示基和通过K-SVD字典学习算法得到的稀疏表示基性能更好.

［1］BARANIUK R G.Compressive Sensing［J］.IEEE Signal Processing Magazine，2007，24（4）：118-121.

［2］LUO C，WU F，SUN J，et al.Compressive data gathering for large-scale wireless sensor networks［C］∥International Confer⁃ence on Mobile Computing and NETWORKING.ACM，2009：145-156.

［3］WU X，XIONG Y，YANG P，et al.Sparsest random scheduling for compressive data gathering in wireless sensor networks［J］.IEEE Transactions on Wireless Communications，2014，13（10）：5867-5877.

［4］WU X，LIU M，WU Y.In-situ soil moisture sensing：Optimal sensor placement and field estimation［J］.Acm Transactions on Sensor Networks，2012，8（4）：1-30.

［5］WANG J，TANG S，YIN B，et al.Data gathering in wireless sensor networks through intelligent compressive sensing［C］∥INFOCOM，2012 Proceedings IEEE.IEEE，2012：603-611..

［6］ZHANG Q，LI B.Discriminative K-SVD for dictionary learning in face recognition［C］∥Computer Vision and Pattern Rec⁃ognition（CVPR），2010 IEEE Conference on.IEEE，2010：2691-2698.

［7］练秋生，石保顺，陈书贞.字典学习模型，算法及其应用研究进展［J］.自动化学报，2015，41（2）：240-260.

［8］RAVISHANKAR S，BRESLER Y.Learning sparsifyingtransforms［J］.IEEE Transactions on Signal Processing，2013，61（5）：1072-1086.

［9］RUBINSTEIN R，PELEG T，ELAD M.Analysis K-SVD：a dictionary-learning algorithm for the analysis sparse model［J］.IEEE Transactions on Signal Processing，2013，61（3）：661-677.

［10］常德宽，张广智，印兴耀.基于学习型DCT字典的3D地震数据随机噪声压制［C］∥中国地球科学联合学术年会.2014.

Research on Low Coherent Representation Basis Learning Algorithm

YANG Yingying
（Department of Basic，Chuzhou Vocational Technology College，239000，Chuzhou,Anhui,China）

Compressive sensing is a new sampling and compression theory.It is widely applied to various sig⁃nals sampling and compression.In this paper，a low coherent representation basis learning algorithm is pre⁃sented，which realizes adaptive representation basis design with sparse projection.Our experimental results show that our proposed algorithm could improve the data recovery quality.

compressive sensing；dictionary learning；low coherence；projection matrix

O 29

A

2095-0691（2017）04-0044-05

2017-04-12

杨颖颖（1982- ），女，安徽濉溪人，硕士，研究方向：课程教学、数学建模、数学文化、应用数学.