基于级联混沌的灰度图像加密算法

赵 凤，姚丽莎

（安徽新华学院，安徽 合肥 230088）

基于级联混沌的灰度图像加密算法

赵 凤，姚丽莎

（安徽新华学院，安徽 合肥 230088）

为提高数字图像在传输中的安全性，本文采用置乱—扩散机制设计一种新的图像加密算法.在像素置乱的过程中，通过Arnold变换和密钥序列排序的方法对图像各像素点位置进行两次置乱.像素值替代是通过对其二进制各位数字置乱后再与密钥序列的异或运算来实现的.而密钥序列都是通过L-L级联映射产生的伪随机序列.实验证明，这种加密算法加密效果好，能够抵御几种常见的攻击方式.

图像加密；L-L级联混沌；置乱；扩散

0 引言

数字图像作为现代信息传输的重要载体，其安全性一直备受各界关注.随着混沌理论发展的逐渐深入和成熟，它已广泛运用到图像加密中.文献［1］提出利用级联混沌映射产生的伪随机码转化为二进制序列与数字图像的二进制进行异或运算得到密文图像，此算法中虽然密钥数量较多，但算法过于简单，易被破译.范延军等［2］提出对图像进行小波变换后，利用Logistic映射和Chebyshev映射交替生成混沌序列与其运算达到置乱加密的目的，极大地提高图像加密的性能.文献［3］先利用Arnold映射和像素排列切割对图像置乱和分块，然后采用Kent-logistic级联混沌与Henon离散混沌的复合系统对像素值扩散，最后再在块内重排，使得图像的像素值和像素位置都被充分打乱.

通过研究发现，单个Logistic映射处于混沌状态的参数值范围较小，密钥空间有限，易受到穷举攻击［4］.另外，Logistic映射中的平凡密钥和拟平凡密钥可能对图像置乱加密无效［2］.而常用的Arnold变换又具有周期性特点，且无法改变图像的直方图特性，所以直接用于图像加密安全性较低.本文为了规避这些风险，综合参考上述文献的思想，利用两个Logistic映射构造成L-L级联混沌映射，并结合Arnold变换和二进制各位的数字变换，设计并实现置乱—扩散机制的图像加密算法，该算法容易实现，具有高安全性，且能抵御常见的几种攻击.

1 混沌序列加密原理

混沌系统就是一种非线性系统.将初值带入混沌函数经过反复迭代形成的序列会变得无规律可循，相关性弱，且具有非周期性和不收敛的特点.这样数量众多、周期很长的信号序列，可以在图像加密时用来作为伪随机码.另外，混沌系统对初始值和结构参数都有很强的依赖性，这使得这种伪随机码不易被模仿.即便知道混沌映射类型，也很难通过猜测其初值和参数去获得同一密钥序列，进而解密.因此，混沌序列作为加密序列广泛运用于密码学中.

主要用到以下两个混沌映射.

1.1 Arnold映射

Arnold映射主要适用于对N*N的图像进行位置的变换，使得图像内容不再清晰可见.其模型如下所示：

式（1）中a,b均为正整数.

但是它的缺点在于具有周期性，反复迭代一定次数后会恢复原图，安全性不高，所以需要经常与其他的方法结合使用对图像位置进行置乱［4-5］.

1.2 L-L级联

离散混沌系统较连续混沌系统算法更简单、运算速度快且复杂度好，所以在图像加密时首选利用离散混沌产生伪随机序列.常用的有Logistic、Tent映射及其改进形式，但它们的Lyapunov指数小、密钥空间较小、安全性较低［3］.王光义等［6］研究发现通过对混沌系统的级联可以有效地提高Lyapunov指数、增强混沌系统的初值敏感性和序列的安全性.本文采用的就是L-L级联混沌系统.

L-L级联即将两个Loigistic映射进行复合，设其参数分别为λ、λ1，映射为

式（2）中xn∈[0,1]，令λ=4,λ1作为分岔参数λ1∈[1.53,4]，对λ1取值只要避开3个周期窗口，系统就处于混沌状态［6］.

2 加密算法的设计

文章通过图像像素位置置乱及像素值替代两个过程来设计算法，本算法主要针对正方形灰度数字图像加密，算法流程图如图1所示：

图1 加密算法流程

2.1 图像像素位置置乱

像素位置置乱步骤如下：

Step1：输入原始N*N灰度图像H，设置初始值：a=1,b=1,A(0)=0.46,λ=4,λ1=3.97；

Step2：利用（1）式Arnold变换生成两个序列xn,yn，用H(xi,yj)替换H(i,j)，形成新的图像H1；

Step3：将H1转化为一维向量，利用级联L-L方程生成混沌序列迭代（500+N*N）次，为消除暂态效应，把舍弃前500项所剩的序列记为A，A进行升序排列后的序列为B，num为B中每一项对应于原序列A中的位置索引. 按序列B的值对H1进行置乱，记位置置乱后的图像为H2，即H2（i）=H1（num（i）），最后将H2还原为N*N矩阵形式.

经过以上3步，两种方式，图像H各像素点的位置得到充分的置乱，置乱后的图像为H2.

2.2 像素值扩散

像素值扩散步骤如下：

Step1：图像H2每个像素灰度值转换成8位二进制数，再将其二进制各位上数字做如下位置变换，形成新的二进制数，再将其转换成对应的十进制像素值，记此时图像为H3.

图2 二进制值变换规则

图2 中表示8位二进制位，从右到左为低位到高位，数字的变化代表对应位置的变化（如原第7位上数字放置在第4位），这样就得到一组新的二进制数.

Step2：再设置一组初始值为C(0)=0.86,λ=4,λ2=2.89，利用级联L-L方程迭代，将前501次舍弃后继续迭代形成的密钥序列记为C，将序列C与图像H3做异或运算，结果记为D.D即为最终加密图像.

解密程序为加密程序的逆过程.

3 加密算法的仿真实现

本文中实验采用的是Matlab 2014a仿真环境，选用240*240的灰度图像Cameraman作为明文.仿真结果如图3所示.

图3 原图及加解密图

4 性能分析

4.1 统计直方图

图像的像素分布不均，容易受到统计攻击，所以对于加密图像的像素分布直方图应尽可能平坦［7］.从图4可以看出原图的像素值分布起伏相差很大，而加密图像与原图的像素值分布完全不同，且趋近于均匀分布，故其具有较好的抗统计攻击能力.

4.2 相邻像素相关性

图像的相邻像素相关性主要从水平、垂直和对角线3个方向的相邻位置来分析［8］.本文对原图和加密图像分别随机选取1 000对相邻像素点做像素值的关系图，如图5和图6所示.

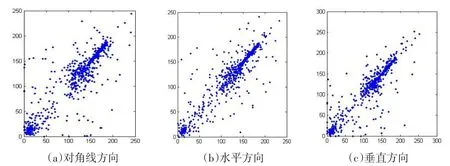
图5 原图像素点相关性分析

图6 加密图像素点相关性分析

从图5可以看出加密后的图像各像素点的邻近像素被充分打乱，像素间无明显相关性.图6中各像素点的分散性可以反映图像置乱程度明显，加密效果显著.

4.3 密钥敏感性分析

密钥敏感性主要是测试在解密的时候对解密密钥做非常微小的变化后，是否还能得到正确的解密图像，它是图像加密安全性分析的一项重要指标，也能体现其抗差分攻击能力［9］.本文将解密密钥key（a=1,b=1,A(0)=0.46,λ1=3.97,C(0)=0.86，λ2=2.89）每次选择一个初始值稍作变化，其他值不变来解密（例如图7（a）修改λ2改为原λ2+0.000 000 000 1=2.890 000 000 1，其他值不变所得的解密图）可得到图7.

图7 修改密钥的解密

从以上实验可以看出，此加密算法至少能保证对密钥做10-10的变化时，都无法解密得到复原图像，该算法对密钥具有高度的敏感性，即使用密钥非常接近的值解密都无效.

4.4 密钥空间分析

本算法中对图像位置置乱和像素值扩散都用到L-L级联混沌映射，选择的是其分岔参数作为密钥，其范围［1.53，4］是单Logistic映射混沌参数范围的近5倍.而经测试，其他密钥（A(0),C(0),λ1,λ2）哪怕对其中一个值变化10-10都不能正确破译加密图像，此密钥组的空间大小近似为1010*4=1040，再加上a、b及二进制变换规则，大大增加破译难度，此系统有较大的密钥空间，可以有效地抵御穷举攻击，故算法的安全性高.

5 总结

本文采用置乱-扩散机制，提出一种基于Arnold映射和L-L级联映射的混合混沌加密算法.仿真结果与算法安全性分析表明：该算法有足够大的密钥空间，对密钥的变化敏感，消除加密图像的相关性，能够抵御统计、穷举、差分等攻击.本算法中选择的是对N*N的图像进行加密，但是如果遇到M*N（假设M＞N）的图像，可以先将图像添加一些特定像素，使其保存为M*M图像后再进行加密，这样既保留图像的全部信息，又能适用此算法.

本算法的优点：1）选用L-L级联混沌不仅函数简洁、易编程实现，又提高Lyapunov指数，改善其动力学特性，扩大密钥空间；2）将Arnold映射与混沌序列排序结合使用，既增强算法的复杂度，又避免由于Ar⁃nold映射的周期性可能引起的图像置乱无效；3）对像素值的二进制序列变换位置，改变其值，加强像素值置乱效果.此算法对灰度图像加密无需多轮操作，较其他算法，更易实现，但是复杂度不低，密钥空间大，加密速度高效.

［1］李赵红，侯建军，张煜，等.基于级联混沌映射的图像加密算法［J］.北京交通大学学报，2005，29（2）：100-102.

［2］范延军，孙燮华，阎晓东，等.一种基于混合混沌序列的图像置乱加密算法［J］.中国图象图形学报，2006，11（3）：387-393.

［3］谢国波，朱润盈.复合级联混沌的彩色图像加密算法［J/OL］.计算机工程与应用，http：//kns.cnki.net/kcms/detail/11.2127.TP.20170331.1911.002.html，2017，3，31.

［4］郭凤鸣，涂立.混沌理论在密码学中的应用［M］.北京：北京理工大学出版社，2015：111-116.

［5］PAN Tiangong，LIDayong.A novel image encryption using Arnold cat［J］.International Journal of Security and Its Applica⁃tion，2013，7（5）：377-386.

［6］王光义，袁方.级联混沌及其动力学特性研究［J］.物理学报，2013，62（2）：020506.

［7］王光义，任国瑞，崔明章，等.基于混沌占空置乱和DNA编码的图像加密算法［J］.计算机应用与软件，2016，33（6）：298-302.

［8］ZHU Congxu，LIAO Chunlong，DENG Xiaoheng.Breaking and improving an image encryption scheme based on total shuf⁃fling scheme［J］.Nonlinear Dynamics，2013，71（1/2）：25-34.

［9］WANG Xingyuan，ZHANG Yingqian，BAO Xuemei.A novel chaotic image encryption scheme using DNA sequenceopera⁃tions［J］.Optics and Lasers in Engineering，2015，73：53-61.

Gray Image Encryption Algorithm Based on Cascade Chaostic

ZHAO Feng，YAO Lisha
（Anhui Xinhua University，230088，Hefei，Anhui，China）

In order to improve the security of digital image in transmission，a novel image encryption algo⁃rithm based on the scrambled-diffusion mechanism is proposed in this paper.In the process of image pixel position permutation，the pixels of the image are twice disordered by the sequence of the Arnold transforma⁃tion and key sequence.The pixel value of the image are substituted by scrambling the number of pixel in bi⁃nary and the XOR operation with key sequence.Pseudo-random sequences produced by the L-L cascade mapping are used as key sequences.The experiment shows that the encryption algorithm has the advantage of good encryption effect and can resist several common cryptogram attacks.

imageencryption；L-L cascading chaotic；permutation；diffusion

TP 391

A

2095-0691（2017）04-0033-05

2017-06-13

安徽省高校自然科学重点研究项目（KJ2015A309）

赵 凤（1985- ），女，安徽太湖人，硕士，主要研究方向为信息安全.