基于改进交叉效率的中国科技创新资源配置研究

范建平，赵园园，吴美琴

(山西大学经济与管理学院，山西 太原 030006)

基于改进交叉效率的中国科技创新资源配置研究

范建平，赵园园，吴美琴

(山西大学经济与管理学院，山西 太原 030006)

科技创新资源优化配置是提高自主创新能力、深化科技体制改革、增强综合国力、推动经济发展的重要措施。从科技创新资源高效配置和异质性动态演化的视角出发，首先将中国除港澳台外31个省市区按照经济发展状况进行区域划分，然后运用六个距离测度与交叉效率集结模型对2014年31个省市区的科技创新能力进行同区域内部评价分析，再利用改进的熵权法确定各区域最优权重，以此区域间交互评价得到的综合效率值作为科技创新资源配置依据，最后对其结果加以分析并给予政策性建议。

科技创新；资源配置；异质性；交叉效率；距离测度；改进熵

1 引言

科技创新资源是完善原有科技水平、提高科技创新能力的各种人、财、物以及信息等四大科技资源的总称[1]。不论是科技创新资源还是一般性资源都具有稀缺特征，合理的资源配置尤为重要。近年来，资源配置也得到了普遍适用。范斐等[2]运用比较优势原理，计算区域各科技资源要素配置效率的相对比较优势。Klingebiel等[3]证实资源配置战略的选择对创新绩效有重大贡献及影响，并将其应用于投资组合。Schlapp等[4]针对研发组合管理中信息资源稀缺问题进行有效配置。Chou等[5]把模糊AHP与模糊DEMATEL方法整合运用到人力科技创新资源的评价当中，强调教育、研发费用等是提高科技创新人力资源能力的基础性评价指标。Wang等[6]设计指标体系对中国31个省市区的科技创新资源配置予以评价，在创新资源的配置水平下采用因子分析和聚类分析将其分为六大区域，进而在每个区域内进行科技创新。因此，优化科技创新资源配置，实施好创新驱动发展战略，使科技通过创新加快向实现生产力转化，为经济社会发展提供强大支撑。

数据包络分析(Data Envelopment Analysis,DEA)起初是由Charnes等提出的用于评价一组基于多投入多产出的同质性决策单元的非参数方法[7]。DEA的主要思想是根据各决策单元自身投入产出情况，试图找到一组最优输入输出权重以确保最大化其加权的产出投入比，该比率就是被评价决策单元的相对效率值。这种以数据驱动的分析方法有效地避免了人为设置指标权重的不科学与不合理性。近年来，创新资源的优化配置是提高自主创新能力、深化科技体制改革的重要措施，因此DEA在科技创新资源配置方面也广泛适用。Zhong等[8]分别运用CCR模型和BBC模型对中国区域科技研发活动进行绩效评价。Lee等[9]运用产出导向的BCC模型和AHP方法对科技资源配置活动中的国家研发活动进行对比分析。但传统意义上讲，传统的DEA模型仍存在一些弊端，诸如仅考虑自评未涉及互评效果、最优权重非唯一、区分力度不够等。为了提高DEA在区分有效决策单元上的能力，Sexton等[10]将他评概念并入DEA中，提出交叉效率评价方法，集结自评与他评效率值来进行综合评价。Du等[11]将DEA交叉效率模型运用到固定成本和资源分配当中。为了克服多重最优输入输出权重的存在，Lotfi等[12]提出了公共权重DEA模型用以对固定资源分配。Doyle等[13]通过引入二次目标确定一组自评权重来计算交叉效率，并提出了仁慈型模型和进取型模型。但在现实生活中，决策单元间并不能简单地用极端的情形分析，同时也不能保证这两种截然相反的情形能够得到相同的排序结果。因此，Wang等[14]提出了中性DEA交叉效率评价方法，试图确定一组输入输出权重使决策单元交叉效率达到最大，同时对其他决策单元无利害性影响。后来Wang等[15]在多准则决策研究的视角下提出了更为中立的模型，即基于虚拟理想与非理想决策单元的距离测度的交叉效率模型。

本文从区域科技创新资源异质性和动态演化的视角出发，首先应用六个基于距离测度和交叉效率集结的新方法研究对2014年中国除港澳台外31个省市区的科技创新能力进行同区域内部资源配置效率评价分析，运用改进的熵权法确定区域内部各省份的权重用以异质区域间的交互评价，然后对OWA算子集结得到综合效率分数及其排序进行分析，再对六个模型下的综合效率分数进行平均集结，最后利用综合效率分数进行科技创新资源的合理配置，并对区域科技创新资源优化提出政策性建议。

2 模型构建

首先介绍了相似度和贴近度方法，并提出了六个基于投入产出指标的理想点与非理想点的距离测度交叉效率模型；然后通过熵权法确定指标权重，在此基础上利用改进熵确定决策单元权重，最后运用OWA算子和平均集结方法得到最终结果。

2.1 距离测度理论

以距离为尺度仅仅能反映两对象之间的位置关系，而不能反映研究对象的势态变化，为了全面客观的考虑方案与正负理想点的关联程度，在相似度的基础上反映方案与理想点的接近程度，为多指标决策问题提供了一种新思路。Wang等[15]提出了一种基于被评价决策单元与正理想决策单元距离的相对贴近度的交叉效率模型，从距离的视角进行的中立性评价。相似性度量法与距离测度密切相关，单值相似度理论是一种决策对象均为精确数的相似程度度量方法。

定义1：设两个精确数值的决策对象a和b，则s(a,b)=1-d(a,b)=1-|a-b|称为决策方案a与b的相似度。

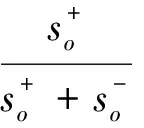
2.2 基于投入产出指标的理想与非理想点的距离测度交叉效率改进模型

在中性交叉效率模型应用理论的基础上引入相似度、贴近度关系理论，事先确定投入产出指标的理想与非理想点，通过距离测度的约束获得的唯一最优输入输出权重更能反映在投入冗余和产出不足方面的差异程度，据此得到的最终交叉效率分数和排序结果更能反映投入产出转化效率。采用标杆管理的方法对被评价决策单元自身的提高与改进有一定参考价值。

定义3：对于被评价决策单元来说，更期望是尽可能少的投入获得尽可能多的产出。因此确定投入、产出指标数据的理想点与非理想点，有利于确定被评价决策单元与理想点与非理想点的相似性度量，如表1所示。

表1 投入产出指标的正负理想点的确定

六个基于距离测度的交叉效率改进模型如下：

模型1：每个决策单元试图确定一组最优输入输出权重以保证被评价决策单元与负理想点的相似度最小化，即避免投入冗余、产出不足的低效率现象发生。具体模型如下：

(1)

模型2：每个决策单元试图确定一组最优输入输出权重以保证被评价决策单元与正理想点的相似度最大化，即试图达到投入少但产出多的高效率状态。具体模型如下：

(2)

模型3：每个决策单元试图确定一组最优输入输出权重以保证最大化正理想点与负理想点的相似度，这样能增强决策单元的优劣区分力度。具体模型如下：

(3)

模型4：每个决策单元试图确定一组最优输入输出权重确保被评价决策单元和正理想点的相似度与被评价决策单元和负理想点的相似度之间的差异度达到最大，以实现高效率的双重效果。具体模型如下：

(4)

模型5：每个决策单元试图确定一组最优输入输出权重确保最小化被评价决策单元与负理想点的相对贴近度。具体模型如下：

(5)

模型6：每个决策单元试图确定一组最优输入输出权重确保最大化被评价决策单元与正理想点的相对贴近度。具体模型如下：

(6)

2.3 熵权法确定指标权重

为避免对模型指标权重主观性及随意性评估，运用熵权法根据被评价对象在相关指标下的数据来客观地确定各评价指标权重的大小，其具体步骤如下：

首先进行标准化处理，计算出各指标的比重qij：

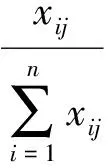
(7)

式中，xij表示第i个决策单元有关第j个指标的原始数值，其中i=1,2,…,n;j=1,2,…,m。

然后，根据qij值计算出第j个指标的熵值ej：

(8)

从而得出第j个指标的权重wj：

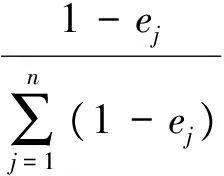
(9)

式中，wj反映了同一指标数值差，wj越大则表明指标的权重越大；反之则越小。

2.4 改进熵确定各决策单元的权重

确定各决策单元的权重是为了将群组内部各成员单元的最优权重进行集结，得到群组整体的最优权重，以便进行群组间的相互评价。因此，本文提出了改进熵法，即将指标赋权后的数据作为处理对象，对数据进行标准化处理，并计算得到各决策单元的相对权重。具体方法如下：

首先计算出各决策单元的比重：

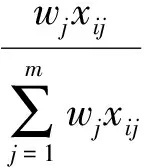
(10)

式中，xij为第i个决策单元的第j个属性的原始数据，wj为第j个属性的权重，wjxij为第i个决策单元的第j个属性的加权之后的数据，且i=1,2,…,n;j=1,2,…,m。

然后，根据Qij值计算出第i个决策单元的熵值ei：

(11)

从而得出第i个决策单元的权重Wi：

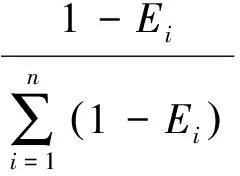
(12)

3 算例

为了验证本文所提出的六个基于距离测度的交叉效率模型的有效性与可行性，运用Wang等[15]算例的相关投入产出数据，如表2所示。然后利用六个改进模型得到被评价决策单元的最终效率分数与排序，最后与Wang等[15]的四个模型结果进行对比分析，其结果如表3所示。

从表3可以看出，本文提出的六个改进模型与Wang等[15]提出的基于虚拟理想与非理想决策单元的距离测度的交叉效率模型的结果基本保持一致，并且更具有稳定性，表明本文所提出的模型合理、适用。

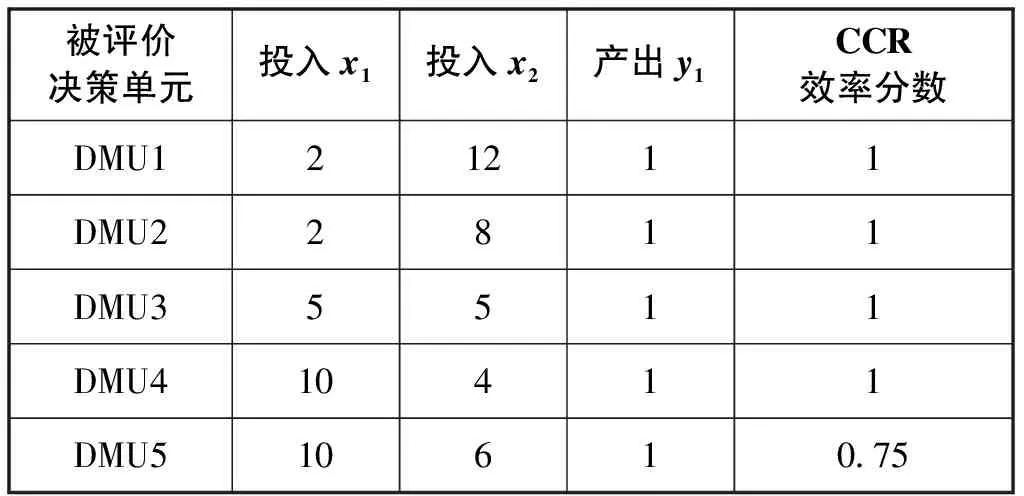
表2 五个被评价决策单元的投入产出数据及其CCR效率值

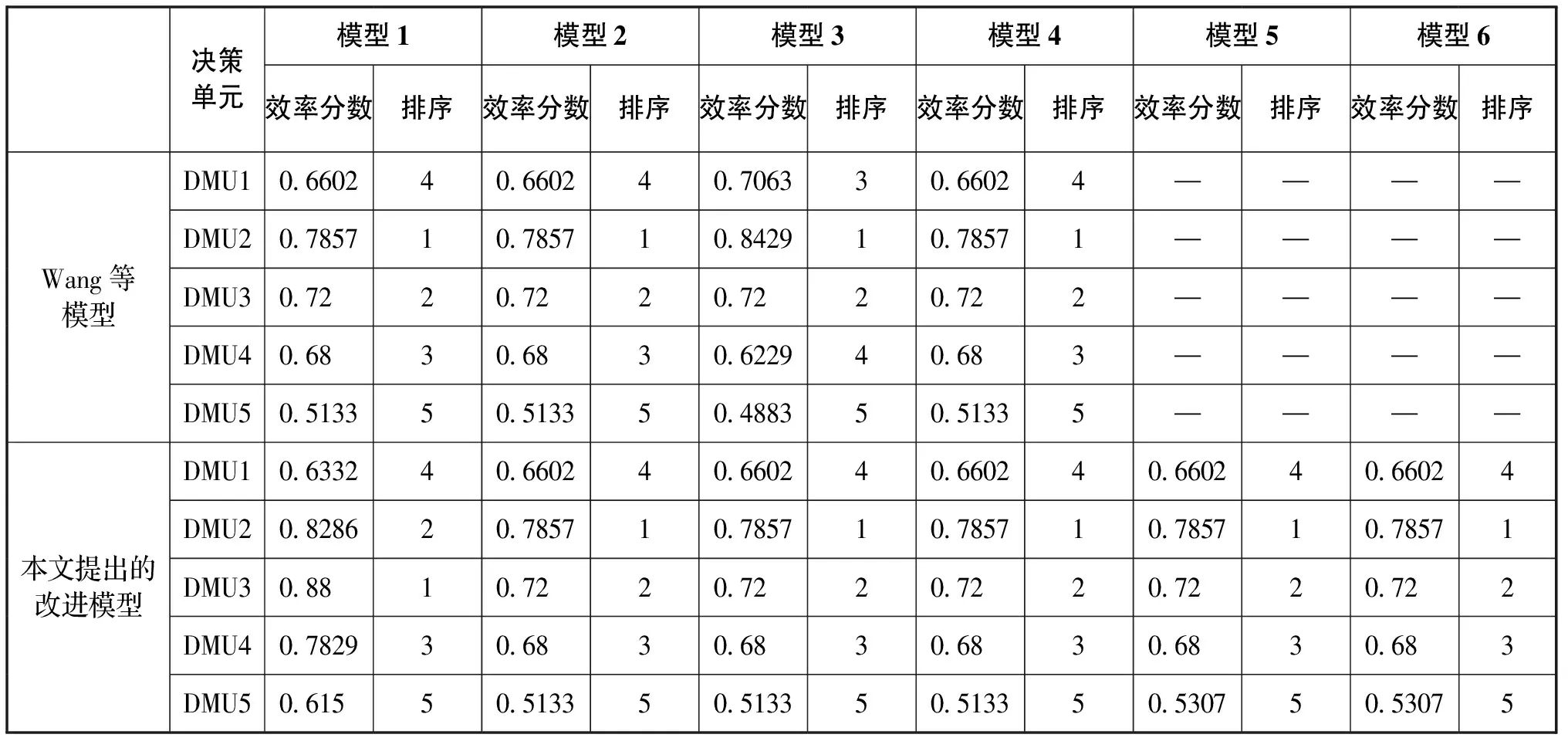
表3 基于六个改进模型与Wang等的结果对比情况

4 应用

科技创新和体制机制创新是形成创新发展的合力所在。当今全社会关心和支持科技创新的氛围日益浓厚，科技资源是科技创造性劳动的基础，科技资源配置能力直接关系到区域经济发展的动力和方向，研究区域科技资源配置效率并进行优化分析更具现实性和必然性，为经济社会发展提供强大支撑。本文从区域科技资源和经济发展异质性视角出发，对2014年中国除港澳台外31个省市区按照经济带发展状况进行划分，如表4所示。选取相关投入产出指标确定区域创新系统科技创新资源的配置效率，相关投入产出指标数据来源于《2015年中国科技统计年鉴》，指标的选取与说明如表5所示。

首先运用六个基于距离测度的交叉效率模型计算各区域内部同质性省市的交叉效率分数和对应的最优输入输出权重；利用改进熵确定各区域内部省市的权重，如表6所示。

表4 除港澳台外31个省市区按经济带划分结果

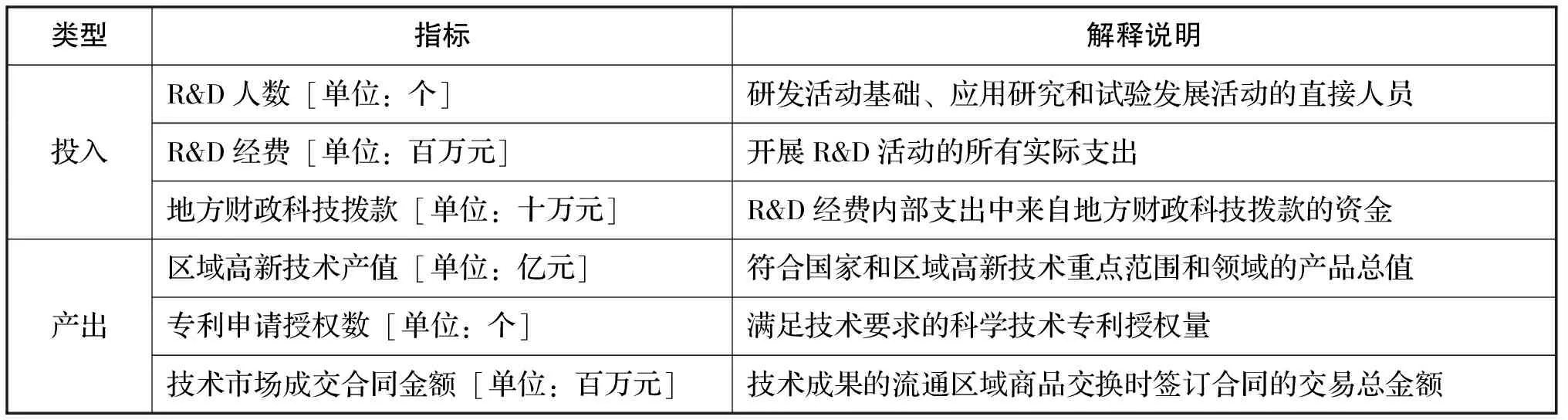
表5 区域创新系统科技创新资源配置效率的相关投入产出指标

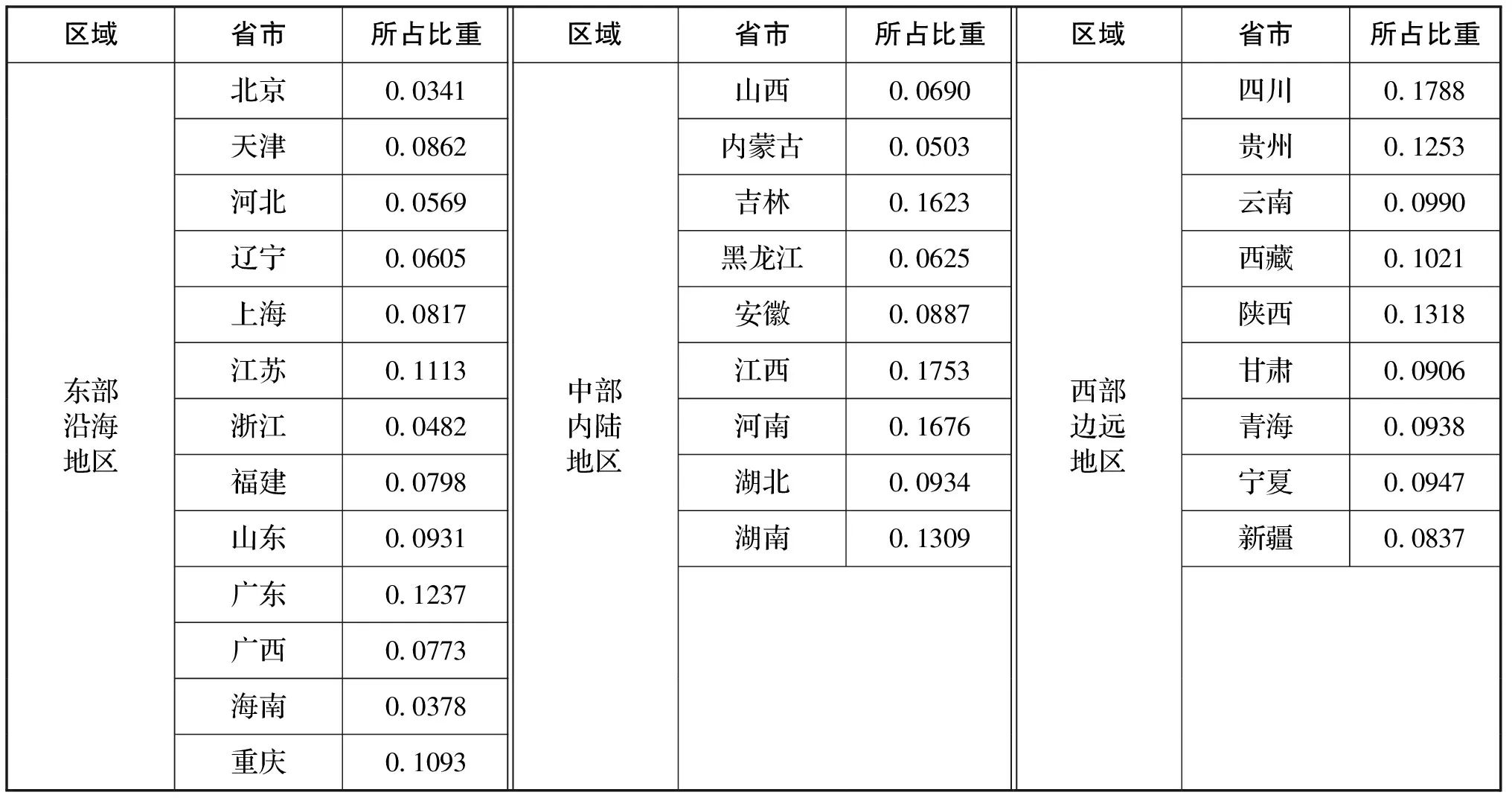
表6 三大区域内部省市所占比重

然后分别在六个基于距离测度的交叉效率模型下，利用同区域内各省市对应的最优输入输出权重与表6中同区域省市的权重，运用OWA算子集结得到区域群组最优输入输出权重，以此进行不同区域间省市的交互评价。这样中国除港澳台外31个省市区的自评与他评效率值进行平均集结得到在六个模型下的交叉评价效率得分。由于六个基于距离测度的交叉效率模型的效用均等，因此对每个省市的六个模型下的交叉效率分数进行平均集结，得到中国除港澳台外31个省市区的综合效率分数及其排序，结果如表6所示。

最后以区域创新系统科技创新发展效率分数作为同区域内部省市资源优化配置的依据，对现有科技资源重新配置。这样既能够对高效发展省市的科技创新绩效有推动作用，也可以对科技创新发展效率低下的省市加以分析与提升，降低投入冗余度，提升整体科技创新绩效水平，结果如表7所示。

从表7中可以看出，东部沿海地区的科技创新资源配置比例是中、西部的一倍有余，东部地区部分省市科技创新资源配置效率相较中、西部而言表现良好，因此大力发展东部沿海地区的科技创新是中国实施创新驱动发展战略的主要动力源泉，但中、西部的转型发展也迫在眉睫，资源配置比例也并非匮乏。此外，存在部分决策单元的效率值大于1的现象，这对科技创新资源配置与优化的结果无重大影响，并且是合乎常理的。由于每个模型下都存在异质群组间的相互评价，互评过程中参照集发生了变化。马占新[31]提出的基于样本点的广义参考集DEA方法中强调传统DEA方法的“评价参考系”是有效决策单元，也就是说传统DEA方法只能获得和有效决策单元比较的信息。但是在现实生活中，人们需要比较的对象不仅仅是“有效单元”，还有其他的参考样本，因此也就出现了与“生产可能集”共存的“样本可能集”。选取样本可能集不同，则对应的有效前沿面也就不同，因此评价的结果也就出现了大于1的情况。超效率的出现能够加大决策单元绩效评价的分区力度，更有利于最终绩效排序。从效率测度的结果看出，综合效率排名前五的有重庆、海南、广东、江苏和贵州，其中重庆、广东、江苏是投入多产出也多，而海南和贵州是收入少、产出少。综合效率分数高，说明这些省市的科技创新资源投入转化为创新产出的能力较强，使投入冗余产出不足的非高效现象降低。而北京、天津、山东、上海等东部沿海发达省市的效率排名却较为滞后，通过比较投入产出指标的数值可以发现，不论是研发的人、财力的投入还是政府财政科技拨款的投入占全国的比重都相对较高，虽然各省市的高新技术产值和技术市场成交合同金额也相对较多，但科技创新资源配置效率相对较低，资源转化能力较差。

图1显示了东部、中部和西部地区中每个省市在基于距离测度交叉效率模型系统中资源配置的不同。从图1(a)中可以看出，东部沿海地区重庆、海南、广东、江苏、福建的配置比例相对较高，而河北、辽宁、上海的科技创新资源配置比例相对较低。本文以现有科技创新资源配置的综合测评效率为依据对各省市进行资源分配。通过对投入产出相关指标数据的观测与比较，效率较高者的资源转化能力较强，资源分配比重相对较大；效率较低者的投入冗余产出不足的现象较为明显，资源分配比重相对较少，使国家科技创新资源充分合理利用。图1(b)中显示了中部内陆地区各省市的科技创新资源配置比例的差异不明显，科技创新能力相对均衡。图1(c)西部边远地区中贵州、青海的资源配置比例相对较高，虽然投入少产出少，但科技创新资源的转化能力相对较高，应该适度加大该省市的科技创新资源的投入，在合理的技术规模能力范围内推动西部边远地区创新能力的发展。

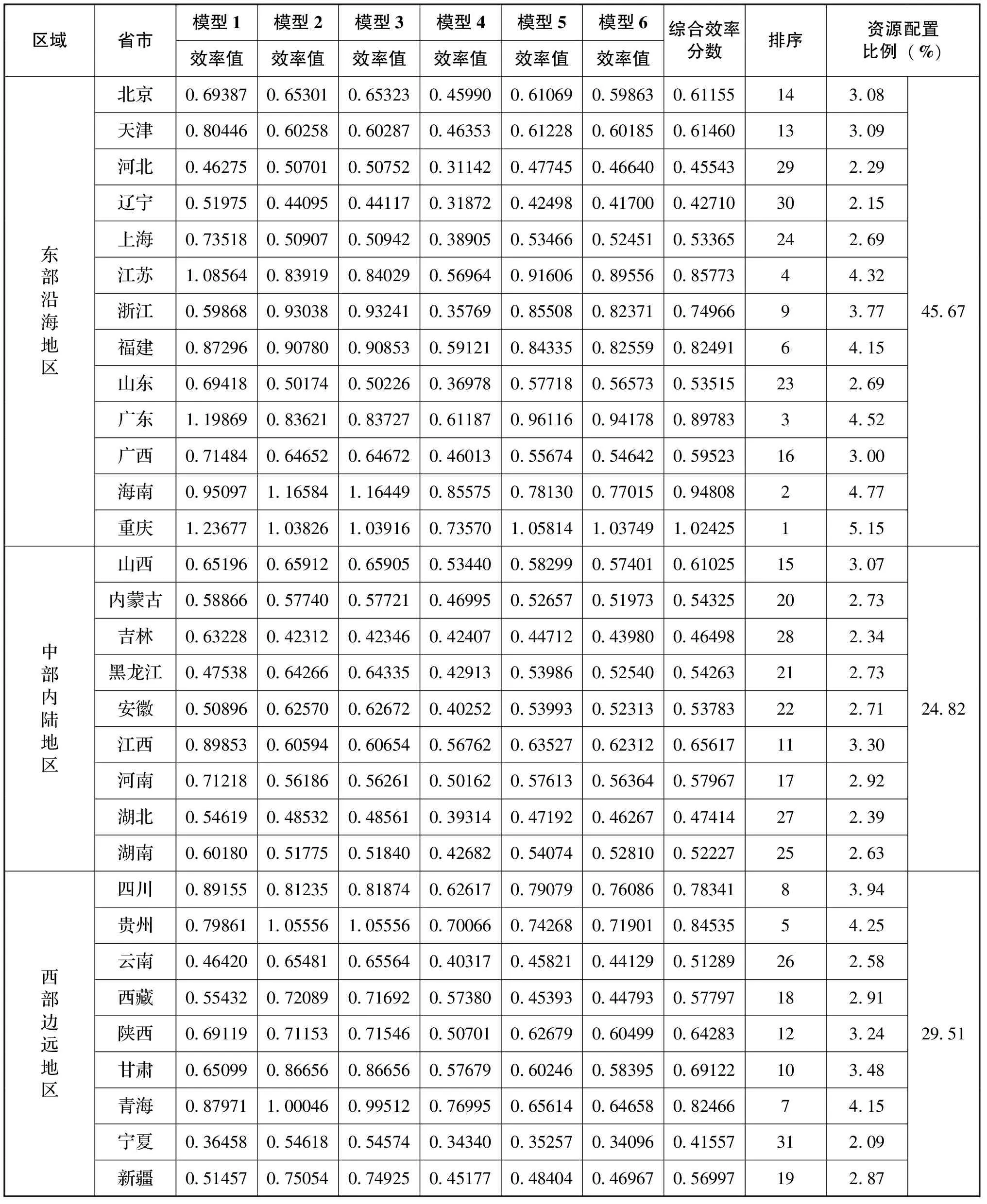
表7 31个省市区的资源配置效率及其优化结果

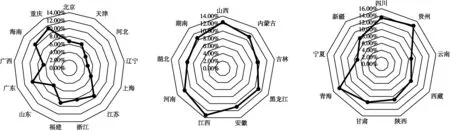
(a)东部沿海地区 (b)中部内陆地区 (c)西部边远地区 图1 三大区域在距离测度交叉效率模型系统中资源配置的比较

基于上述实证分析结果，本文提出以下促进区域科技创新资源优化配置的政策建议：①东部沿海地区的科技创新资源相比中、西部较为丰富，但投入冗余造成区域科技创新资源配置效率降低。由于东部沿海地区仍是中国科技创新发展的主要推动区域，因此加强东部沿海地区的创新资源投入转化为创新产出的能力是提高东部沿海地区省市创新驱动发展的重要举措。②中部内陆地区的科技创新发展水平相较均衡，并且科技创新资源并非匮乏，通过转型升级调整结构，以政府为主导、企业为主体，结合区域特有优势推动中部内陆地区省市的科技创新。③位于西部边远地区的贵州、青海的科技创新资源配置效率相较东、中区域的绝大多数省市的效率要高，但投入资源的不足导致创新产出占全国份额较少，加强智力资本的投入是加强西部边远地区科技进步的关键。东部与中西部人才资源配置不均衡，应适当加强人才引入对拓展科技创新视野、提高科技创新能力有一定推动作用。④为完善科技创新发展激励政策，优化有限科技资源的配置策略，政府应当充分发挥“推手”作用。政府在引导资金的配置基础上，调动社会、企业的技术研发投入的积极性，大力推动协同创新，加强资源的统筹协调和开放共享，使科技创新发展成为多部门多领域多区域合力攻关的新目标，真正实现万众创新。

5 结语

(1)使用六个不同的基于距离测度的交叉效率模型能够避免单一模型测度的局限性与片面性，平均集结模型系统是一种更具说服能力和辨识力度的测量方法。

(2)充分考虑到决策单元的异质性，以熵权法确定指标权重，改进熵确定决策单元权重，得到的群组最优输入输出权重进行异质群组间的交叉绩效评价，考虑问题更为全面。

(3)综合效率值作为资源优化配置的依据更具有理论意义，绩效分数反映资源投入转化为产出的能力，为高效决策单元配置更多资源有利于整体效率的提升。

[1]王雪原,王宏起.我国科技创新资源配置效率的DEA分析[J].统计与决策,2008(8):108-110.

[2]范斐,杜德斌,李恒.区域科技资源配置效率及比较优势分析[J].科学学研究,2012,30(8):1198-1205.

[3]KLINGEBIEL R,RAMMER C.Resource allocation strategy for innovation portfolio management[J].Strategic management journal,2014,35(2):246-268.

[4]SCHLAPP J,ORAIOPOULOS N,MAK V.Resource allocation decisions under imperfect evaluation and organizational dynamics[J].Management science,2015,61(9):2139-2159.

[5]CHOU Y C,SUN C C,YEN H Y.Evaluating the criteria for human resource for science for science and technology(HRST)based on an integrated fuzzy AHP and fuzzy DEMATEL approach[J].Applied soft computing,2012,12(1):64-71.

[6]WANG X Y,WANG H Q.Comparison research of science and technology(S&T)innovation resources allocation level of each district in China[C].International Conference on Management Science and Engineering-Annual Conference Proceedings,2008:1537-1542.

[7]CHARNES A,COOPER W W,RHODES E L.Measuring the efficiency of decision making units[J].European journal of operational research,1978,2(6):429-444.

[8]ZHONG W,YUAN W,LI S X,et al.The performance evaluation of regional R&D investments in China:an application of DEA based on the first official China economic census data[J].Omega,2011,39(4):447-455.

[9]LEE H,PARK Y,CHOI H.Comparative evaluation of performance of national R&D programs with heterogeneous objectives：a DEA approach[J].European journal of operational research,2009,196(3):847-855.

[10]SEXTON T R，SILKMAN R H，HOGAN A J.Data envelopment analysis：critique and extensions[J].New directions for program evaluation，1986(32):73-105.

[11]DU J,COOK W D,LIANG L,et al.Fixed cost and resource allocation based on DEA cross-efficiency[J].European journal of operational research,2014,235(1):206-214.

[12]LOTFI F H,HATAMI-Marbini A,AGRELL P J,et al.Allocating fixed resources and setting targets using a common-weights DEA approach[J].Computers&industrial engineering,2013,64(2):631-640.

[13]DOYLE J，GREEN R.Efficiency and cross efficiency in DEA：derivations，meanings and the uses[J].Journal of the operational research society,1994,45:67-578.

[14]WANG Y M,CHIN K S.A neutral DEA model for cross-efficiency evaluation and its extension[J].Expert systems with applications,2010,37(5):3666-3675.

[15]WANG Y M,CHIN K S,LUO Y.Cross-efficiency evaluation based on ideal and anti-ideal decision making units[J].Expert systems with applications,2011,38(8):10312-10319.

[16]马占新.广义参考集DEA模型及其相关性质[J].系统工程与电子技术,2012，34(4):709-714.

ChineseScienceandTechnologyInnovationResourcesAllocationBasedontheImprovedCross-EfficiencyMethod

Fan Jianping，Zhao Yuanyuan，Wu Meiqin

(School of Economics and Management，Shanxi University，Taiyuan 030006，China)

The optimal allocation of scientific and technological innovation resources is an important measure to improve the capability for independent innovation，deepen the reform of scientific and technological system，enhance the comprehensive national strength，and promote economic development.It is studied from the perspective of efficient allocation of scientific and technological innovation resources and dynamic evolution of non-homogeneity.First of all，according to the economic development，the thirty-one provinces and cities,which are not including Hong Kong，Macao and Taiwan in China,are divided into three regions.Next，the paper uses six aggregation models of distance measure and cross efficiency to analyze and evaluate the ability of scientific and technological innovation of these 31 provinces and cities in 2014.Then，it applies the improved entropy method to determine the regional optimal weights by which to evaluate interactively between regions.On the basis of the regional optimal weights，comprehensive efficiency evaluation value is obtained as scientific and technological innovation resources allocation.Finally it analyzes the results and makes policy suggestions.

Science and technology innovation；Resources allocation；Non-homogeneous; Cross-efficiency；Distance measure；Improved entropy

2017-03-02

范建平(1975-)，男，山西人，博士，副教授；研究方向：决策科学与技术。

G311

A

(责任编辑 沈蓉)