基于谱线形状与信息量差异的高光谱解混NMF初始化方法

袁德有， 袁 林

(1.南阳理工学院数学与统计学院,南阳 473004； 2.南阳理工学院经济管理学院,南阳 473004)

基于谱线形状与信息量差异的高光谱解混NMF初始化方法

袁德有1， 袁 林2

(1.南阳理工学院数学与统计学院,南阳 473004； 2.南阳理工学院经济管理学院,南阳 473004)

在高光谱像元解混应用中，好的端元光谱矩阵初始化方法对于提高盲信号分解精度具有重要意义。针对空间分辨率较高的高光谱数据，提出了一种新的面向非负矩阵分解(non-negative matrix factorization，NMF)的初始化方法。该方法通过计算像元在谱线形状和信息量差异等方面的参数，利用像元谱线峭度、KL散度和光谱角等参量，从众多混合像元中识别出纯像元； 并分辨出不同类型纯像元(或类纯像元)之间的差别，从中选择最适合代表每一类型端元的纯像元(或类纯像元)作为算法的初值像元，完成端元矩阵的初始化。将此方法分别用于模拟数据和真实数据的实验结果表明，该方法能够明显提高高光谱混合数据的NMF精度，相比其他常用初始化方法具有更好的效果。

初始化； 盲信号分解； 非负矩阵分解(NMF)； 谱线形状； 信息量差异

0 引言

非负矩阵分解(non-negative matrix factorization，NMF)技术，由于其“非负性约束”和“局部构成整体”的概念符合人们的日常感知习惯，同时还具有物理意义明确、实现简便、占用存储空间少等优点，因此得到了广泛应用[1]。近年来，研究人员开始将NMF引入到高光谱像元解混应用中[2]； 但在取得一定研究成果的同时，也带来了不少问题，初始化就是其中之一。NMF是一个迭代过程，需要确定初始值； 好的初始值可以加快算法收敛速度，提高分解精度。但目前的NMF算法多采用取随机值、主成分分析(principle component analysis, PCA)、奇异值分解[3](singular value decomposition，SVD)和模糊C均值聚类[4](fuzzy C-mean cluster, FCM)等方法进行初始化。随机初始化最简单，但效果往往也最差； 其他方法多是从文本分类[5]、语音处理等领域移植过来的，不能很好地符合高光谱混合数据的特点，实际应用效果不甚理想[6]。为此，本文主要针对空间分辨率相对较高、地物分布不太复杂的高光谱混合数据，在端元类型和混合特性未知的前提下，为解决利用NMF进行像元盲分解时的初始化问题，提出一种新的综合像元谱线形状特征及信息量差异特征等信息的初始化方法。该方法基于如下假设： 对于场景中每一类型的端元，高光谱数据中至少含有一个对应的纯像元或类纯像元(部分混合像元中，光谱和反射率特性等与占主导地位的某一种端元类似的像元，本文称之为“类纯像元”)。

1 初始化的目标与关键

用于高光谱像元解混的NMF算法，其初始化分为2部分： ①端元光谱矩阵W; ②丰度矩阵H。由于大多数真实高光谱数据的端元混合情况未知，因此H只需要采取随机生成的方式，同时满足非负性约束和全加性约束即可。端元提取是高光谱像元解混的关键步骤，也是地物类型识别和丰度反演的基础和前提，目前尚缺少高效的W初始化方法，所以本文主要研究W的初始化方法。

W初始化的目标，即从原始高光谱数据的众多像元中，选择每类端元对应的一个纯像元(或类纯像元)，将其对应光谱值作为NMF算法初始值。难点在于，要选出最能代表每类端元的一个像元，并保证没有遗漏和重复，否则将对结果造成不利影响。

选择各类型端元对应的纯像元(或类纯像元)关键在于： ①从众多混合像元中识别出纯像元； ②分辨出不同类型纯像元之间的差别，保证选择结果在端元类别上没有重复。这样，每类端元都有且仅有一个纯像元(或类纯像元)作为初始值参与NMF运算，从而实现对真实W的最优近似。

2 初始化方法

首先需要确定端元数量，进而确定要选择的波段数量。可利用PCA、最小噪声分离(minimum noise fraction，MNF)和SVD等方法估计高光谱数据的端元数量[7-8]。本文选择PCA变换确定波段数，设x={x1,x2,…,xn-1,xn}为一个像元所有n个波段光谱响应信号组成的向量，则X={x1,x2,…,xN-1,xN}就是由图像中所有N个像元对应向量组成的矩阵。用PCA方法对X进行处理，得到一系列主成分分量，以及它们所对应的特征值，特征值的大小与各主成分分量的信息含量相对应。所以，观察特征值的分布情况，确定大特征值的数目k，就可估计出该高光谱图像覆盖区域的端元数目。

k的确定可采用以下方法： 设定一个阈值(如99.73%)，假设前k个主成分分量对应的特征值累加占总特征值λ的百分比为p，即

(1)

若达到阈值要求，则k即为所求端元数目。确定端元数量后，主要基于像元的谱线形状和光谱信息量差异2个方面进行初始化。首先研究像元的谱线形状，包括像元本身谱线形状的特点，以及像元之间谱线形状的差异。为了利用像元本身的谱线形状从众多混合像元中识别出纯像元，本文参考了独立成分分析(independent component analysis，ICA)理论和中心极限定理。可以推知，纯像元(端元)或类纯像元的谱线形状趋于非高斯分布，混合程度高的像元谱线趋于高斯分布。因此，可通过计算像元谱线的非高斯化程度来标识像元的纯度。

峭度(kurtosis)是曲线非高斯性的自然度量指标[9]，其计算公式为

(2)

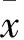
需要特别注意的是，K的阈值设置要适度，过小会使混合程度较高的像元无法剔除； 而过大则会将部分谱线形状非高斯性相对较弱的纯像元排除。多次实验结果表明，K的阈值取K平均值的0.6倍以下时，基本不会发生误排除纯像元的情况。本文试验中K的阈值取K平均值的0.5倍。利用K选出第一个初值像元，并留下绝大多数纯像元(或类纯像元)。

接下来分辨不同类型纯像元之间的差别。本文利用KL散度(Kullback-Leibler divergence)和光谱角(spectral angle, SA)[7]2种参数，通过综合像元间的信息量差异和谱线形状差异，得出像元间光谱差异的定量指标； 然后选择与已选初值像元之间光谱差异最大的像元，使得选出的初值像元是能够分别代表所有种类端元的纯像元(或类纯像元)。

一般而言，同种端元对应的纯像元(或类纯像元)之间光谱差异很小，反之异种端元对应的纯像元(或类纯像元)之间光谱差异则较大[8]。通过计算待选像元与已选像元之间光谱信息的KL散度，选出最大KL散度对应的待选像元，即可选出与已选像元不属于同一端元种类的纯像元或纯度很高的类纯像元。

对于离散随机变量，其概率分布P和Q的KL散度DKL(P‖Q)定义为

(3)

KL散度仅当概率P和Q各自总和均为1，且对于任何i，均满足P(i)>0及Q(i)>0时才有意义。

NMF分解结果中还包含了各类端元的谱线形状信息。因此，初始化时也应加入对像元间谱线形状差异的度量。本文利用光谱角来度量像元间的谱线形状差异。

2个像元t和r之间SA的计算公式为

(4)

式中i为波段序号。

通过计算KL散度和SA参数，并将二者作加权和(本文实验中，根据多次实验结果，权重系数比值定为0.6)，可更加全面地度量像元间的光谱特性差异。在初值选择的每次迭代过程中，选择具有最大加权和的像元，就能够有效地保证新选像元与所有已选像元均分属于异类端元。

3 初始化流程

W初始化方法流程如图1所示。

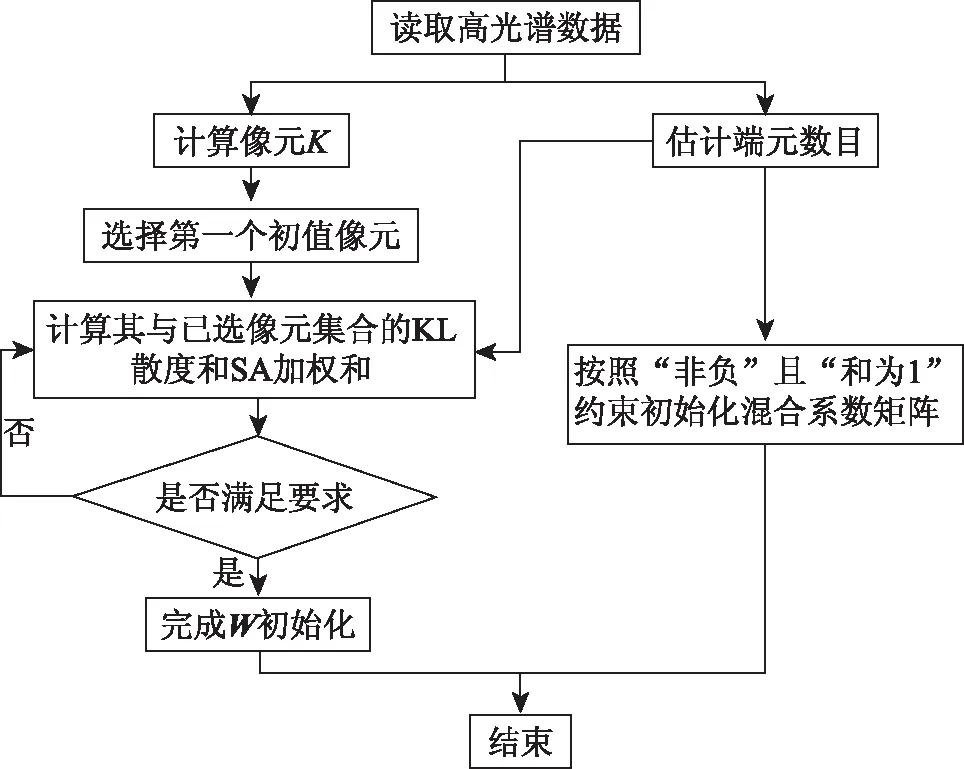
图1 W初始化流程Fig.1 Flowchart of initialization for W

初始化方法步骤如下： ①读取数据，转换数据维度； ②估算需要选择的初值像元数量(PCA等)，并计算所有像元谱线的K，选出第一个初值像元； ③完成混合矩阵(H)的初始化； ④计算候选像元与已选像元集合之间KL散度和SA的加权和，确定新的初值像元； ⑤重复步骤④，直到选择的初值像元数量满足要求； ⑥根据选择的所有初值像元，完成W的初始化； ⑦按照“非负”且“和为1”的条件约束初始化混合系数矩阵。

4 实验与分析

4.1 模拟数据实验

模拟数据为长和宽各10个像元、波段数为224的高光谱图像，波长范围约为0.4～2.5 μm，组成100行、224列的混合像元矩阵。该矩阵由端元矩阵和混合矩阵相乘得到，其中，端元矩阵由5种ENVI标准光谱库中的端元数据(黑色涂料、沥青、煤渣、松木和水泥)组成，共5行、224列； 混合矩阵为所有元素同时满足“和为1”且“非负”2个约束条件的随机数矩阵，共100行、5列。将混合像元矩阵的第15,25,35，45和75个像元重新赋值为纯像元，分别对应5种端元。5种端元的光谱曲线图如图2。

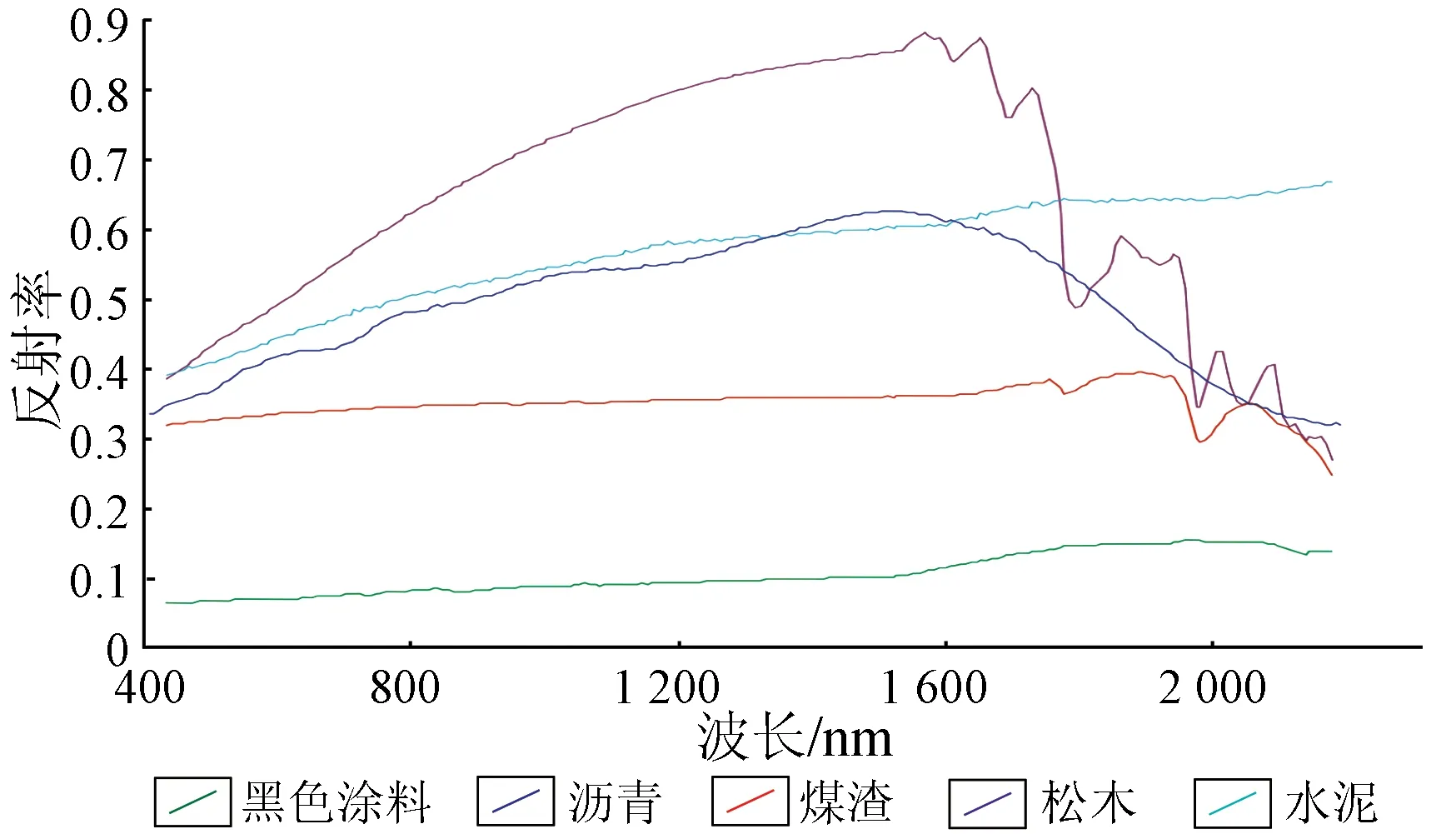
图2 5种端元初始光谱曲线Fig.2 Spectral curves of five end-members

对模拟数据的100个混合像元按1～100依次编号，则本文方法选中的初值像元序号(按照选择的顺序)依次为： 35，25，75，45和39，按照序号大小顺序依次为： 25，35，39，45和75。其中，序号为25，35，45和75的4种像元都被准确选出，序号为15的像元则被误选为序号为39的像元。究其原因，可能是由于直接将15号像元赋值为纯像元时，较严重地偏离了“和为1”的约束。

利用本文方法得到初始像元光谱(图2)，以该结果对NMF基本算法进行初始化，得到的NMF分解结果中端元波形如图3所示。

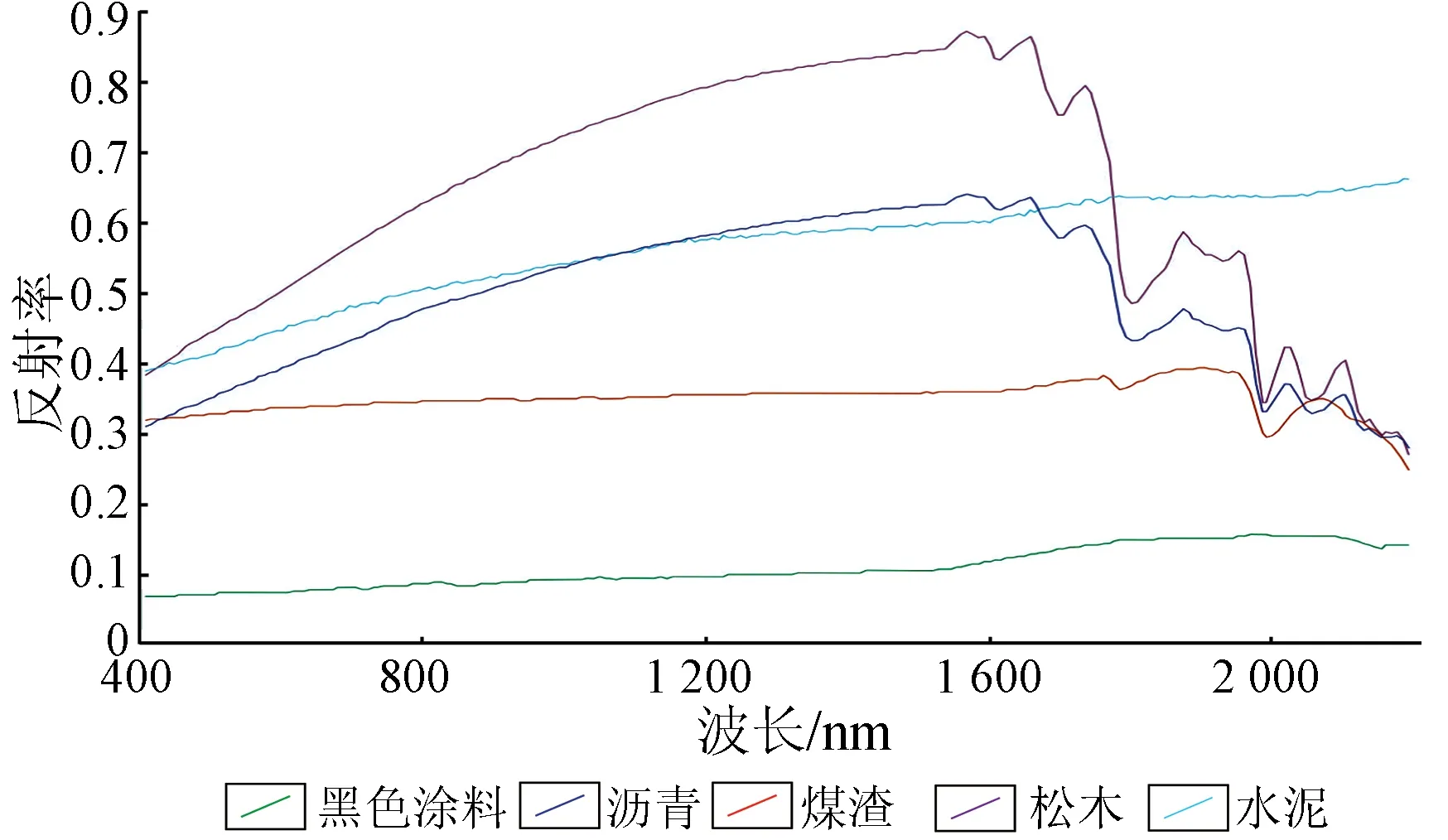
图3 NMF分解结果Fig.3 NMF decomposition results

从图3可以看出，NMF分解结果中的端元波形与初始端元光谱十分相似。进一步应用本文初始化方法的NMF端元估计结果，以其与真实端元之间SA的均方根误差(root mean square error，RMSE)为度量参数，进行精度分析和对比。首先，计算NMF基本算法(应用本文方法进行初始化)端元估计结果和真实端元之间的SA，得到矩阵

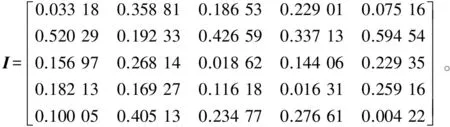
(5)

每行的最小值为5种真实端元光谱与对应的NMF端元光谱分解结果的SA，分别为0.033 18，0.192 33，0.018 62，0.016 31和0.004 22，RMSE为0.088 0。

为了更加直观，图4分别列出了5种真实端元光谱和NMF结果中对应波形估计的细节对比。

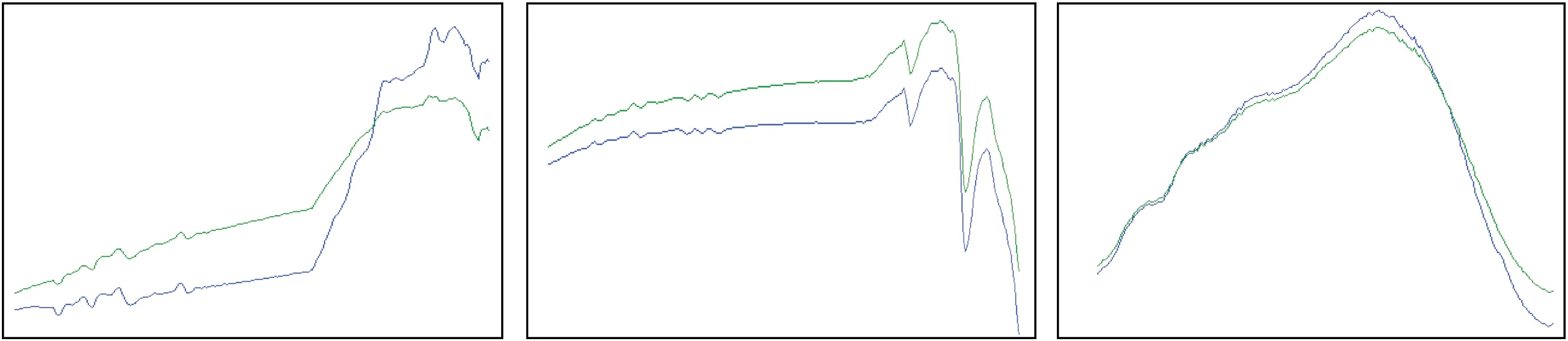
(a) 端元1 (b) 端元2 (c) 端元3

(d) 端元4(e) 端元5

图4真实端元和对应NMF分解结果的光谱细节对比

Fig.4Detailedcomparisonbetweenspectralcurvesofrealend-membersandcorrespondingNMFdecompositionresults

从图4可知，除图4(b)中所示的端元2的波形估计误差(与真实端元光谱间SA为0.192 33)偏大以外，其余4种端元估计的统计误差和实际光谱形状误差均非常小，只有较明显的幅度误差，这4种端元都被很好地识别和估计出来。

表1列出了本文方法与其余几种常用初始化方法的分解精度对比结果； 表2列出了在不考虑分解效果最差的一个端元(图4(b)所示端元2)时，本文方法与原理较为类似的顶点成分分析(vertex component analysis，VCA)方法的精度比较。

表1 模拟数据实验中本文方法与其他几种常用初始化方法的分解精度对比Tab.1 Comparison between decomposition accuracies of method proposed in this paper and several other initialization methods in experiment of simulated data

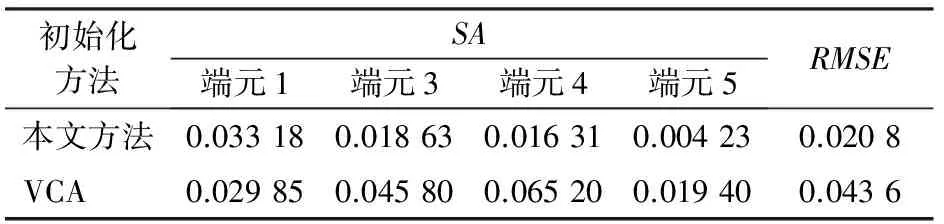
表2 剔除一个精度最差的端元 (端元2)后本文方法与VCA的精度对比Tab.2 Comparison between accuracies of method proposed in this paper and VCA method without considering the worst estimated end-member (end-member 2)

从表1可以看出，在利用NMF算法进行盲分解时，本文方法相比其他大多数初始化方法，可以获得更精确的分解结果； 但由于其中一个端元(端元2)的分解误差较大，导致其整体精度略低于VCA。

从表2可以看出，本文方法比VCA的局部精度更高。具体而言，就是在不考虑误差最大的一个端元(端元2)时，本文方法相对VCA精度更高。若假设误差最大的端元为非感兴趣信息，将其视为背景噪声，只要求准确分解出数据中部分感兴趣端元的光谱信息，则本文方法相对VCA将更具有优势。

4.2 真实数据实验

选取的真实实验数据为美国圣地亚哥市的AVIRIS高光谱数据。该数据的光谱范围为0.4～2.5 μm，光谱分辨率为10 nm，波段数为224个(剔除无效或噪声较大波段以及水汽吸收波段后，实际有效波段数为189个)； 空间分辨率为3.5 m，图像行、列数均为40。

该数据中含有感兴趣地物类型主要包括4种地物，其余类型的小目标作为背景噪声加以忽略。4种地物的光谱真值如图5(a)所示，图5(b)为应用本文方法进行初始化后的NMF分解结果。

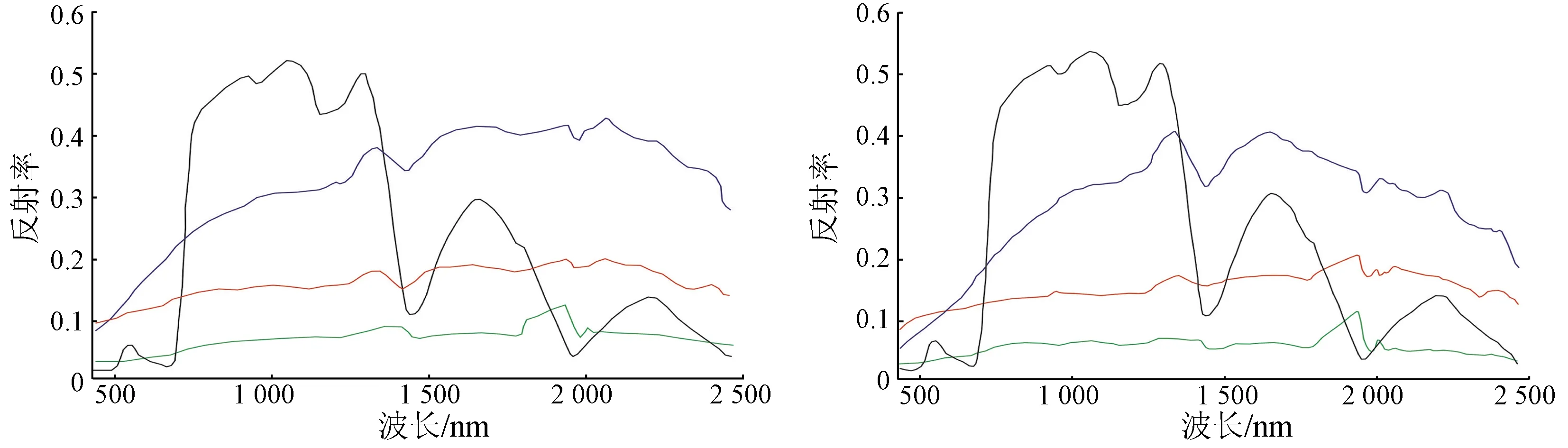
(a) 4种地物光谱真值 (b) NMF分解结果

图54种地物光谱真值与NMF分解结果对比

Fig.5ComparisonbetweenoriginalspectralandNMFdecompositionresultsforfourkindsofgroundobjects

表3列出本文方法与其余几种常用初始化方法的分解精度对比结果。

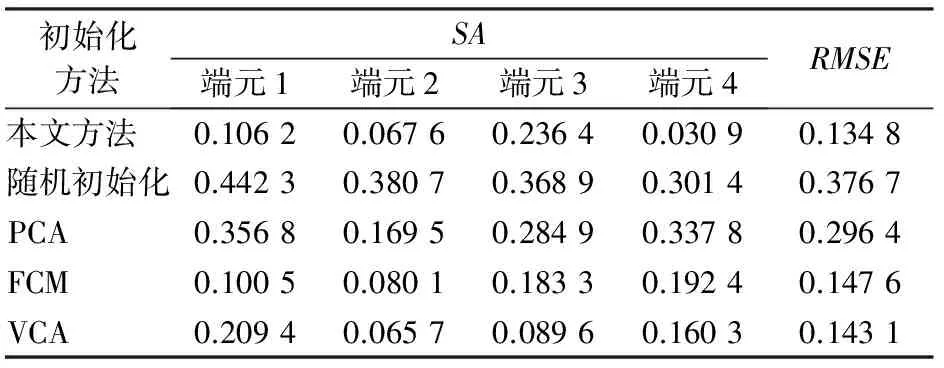
表3 真实数据实验中本文方法与其他几种常用初始化方法的分解精度对比Tab.3 Comparison between decomposition accuracies of method proposed in this paper and several other initialization methods in experiment of real data

从表3可以看出，本文方法应用于真实数据时的精度略低于模拟数据，但相对其他常用方法仍具有更高的精度。与模拟数据实验结果相反，本文方法应用于真实数据的精度略微高于VCA，与FCM精度也非常接近。首先，上述结果证明了本文方法在应用于真实数据时的可行性； 其次，也说明本方法的性能尚不够稳定，处理的数据不同时，相对其他方法的精度也有所不同。

5 结论

本文针对缺少像元混合信息，同时含有纯像元(或类纯像元)的高光谱数据盲分解过程，提出一种新的非负矩阵分解(NMF)初始化方法。该方法利用像元谱线峭度、KL散度和光谱角等参量，从众多混合像元中识别出纯像元，并分辨出不同类型纯像元之间的差别，从中选出最有资格代表各类型端元的纯像元或类纯像元作为初值像元，完成端元光谱矩阵的初始化。实验结果说明，该方法能有效提高NMF算法的精度，比其他大多数常用初始化方法具有更好的效果。

需要强调的是，本文方法基于选择已有像元作为初值，并要求高光谱数据中具有每种端元对应的纯像元(或类纯像元)，这一前提对于部分真实高光谱数据(例如空间分辨率很低、场景内地物分布情况和纹理复杂的高光谱数据)，是难以满足或难以确定是否满足的，这就限制了该方法的适用范围。另外，该方法的性能尚不够稳定； 在峭度阈值判断中，权重系数的选择主要依靠经验和实验结果来确定，尚缺乏具体流程和理论依据。因此，下一步的工作主要包括如何扩展本文方法的适用范围及如何确定权重系数选择的流程和理论依据。

[1] Berry M W,Browne M,Langville A N,et al.Algorithms and applications for approximate nonnegative matrix factorization[J].Computational Statistics and Data Analysis,2007,52(1):155-173.

[2] 李二森,张保明,杨 娜,等.非负矩阵分解在高光谱图像解混中的应用探讨[J].测绘通报,2011(3):7-10.

Li E S,Zhang B M,Yang N,et al.Discussion of the NMF’s application for hyperspectral imagery unmixing[J].Bulletin of Surveying and Mapping,2011(3):7-10.

[3] Boutsidis C,Gallopoulos E.SVD based initialization:A head start for nonnegative matrix factorization[J].Pattern Recognition,2008,41(4):1350-1362.

[4] Alshabrawy O S,Ghoneim M E,Awad W A,et al.Underdetermined blind source separation based on fuzzy C-means and semi-nonnegative matrix factorization[C]//Proceedings of 2012 Federated Conference on Computer Science and Information Systems.Wroclaw,Poland:IEEE,2012:695-700.

[5] 翟亚利,吴 翊.NMF初始化研究及其在文本分类中的应用[J].计算机工程,2008,34(16):191-193,197.

Zhai Y L,Wu Y.Study of non-negative matrix factorization initialization and its application to text classification[J].Computer Engineering,2008,34(16):191-193,197.

[6] Lee D D,Seung H S.Algorithms for non-negative matrix factorization[C]//Proceedings of the 13th International Conference on Neural Information Processing Systems.Denver,CO:ACM,2000:535-541.

[7] 余先川,安卫杰,吕中华,等.一种基于光谱角和光谱距离自动加权融合分类方法[J].地质学刊,2012,36(1):33-36.

Yu X C,An W J,Lyu Z H,et al.Automatic weighting fusion classification method based on spectral angle and spectral distance[J].Journal of Geology,2012,36(1):33-36.

[8] Wang R J,Zhan Y J,Zhou H F.RETRACTED:A method of underdetermined blind source separation with an unknown number of sources[J].Engineering Applications of Artificial Intelligence,2011:556-562.doi:10.1016/j.engappai.2011.06.003.

[9] 毋文峰,陈小虎,苏勋家,等.基于峭度的ICA特征提取和齿轮泵故障诊断[J].机械科学与技术,2011,30(9):1583-1587.

Wu W F,Chen X H,Su X J,et al.ICA feature extraction and fault diagnosis based on Kurtosis for a gear pump[J].Mechanical Science and Technology for Aerospace Engineering,2011,30(9):1583-1587.

Aninitializationmethodofnon-negativematrixfactorizationforhyperspectraldataunmixingbasedonspectralshapeandinformationdissimilarity

YUAN Deyou1， YUAN Lin2

(1.SchoolofMathematicsdissimilarityandStatistics，NanyangInstituteofTechnology，Nanyang473004，China；2.SchoolofEconomicsandManagement，NanyangInstituteofTechnology，Nanyang473004，China)

When blind signal separation technique is applied to unmixing hyperspectral data, a good initialization is vital for improving separating precision. Aimed at the hyperspectral data with relatively high spatial resolution and simple surface features, the authors put forward a reasonable hypothesis that the data contain pure pixel or approximate pure pixel corresponding to the each type of end-members, and proposed a new initialization method of non-negative matrix factorization(NMF), which has great potential in pixel unmixing. By calculating parameters to quantify the spectral shape and information difference among candidate pixels, this method extracts pure pixels from mixed pixels, recognizes the information dissimilarity among different types of pure pixels and choose the existing pixels that are most suitable for representing each type of end-members as NMF’s initial values. The experimental results show that the method proposed in this paper can improve NMF’s decomposition accuracy of hyperspectral data significantly, and its performance is better than that of other NMF initialization methods.

initialization； blind signal separation； non-negative matrix factorization(NMF)； spectral shape； information dissimilarity

10.6046/gtzyyg.2017.04.17

袁德有,袁林.基于谱线形状与信息量差异的高光谱解混NMF初始化方法[J].国土资源遥感,2017,29(4)：114-119.(Yuan D Y,Yuan L.An initialization method of non-negative matrix factorization for hyperspectral data unmixing based on spectral shape and information dissimilarity[J].Remote Sensing for Land and Resources,2017,29(4)：114-119.)

TP 751

A

1001-070X(2017)04-0114-06

2016-12-16；

2017-02-27

河南省高等学校重点科研项目“Smith正规型在有限域上有理点个数中的应用”(编号： 17A110010)资助。

袁德有(1960-),男,教授,主要从事小波分析等方面的研究。Email： yuandeyou1960@163.com。

(责任编辑：张仙)