基于树高-年龄分级的杉木人工林多形立地指数曲线模型研究

朱光玉 ，康 立 ，何海梅 ，吕 勇 ，银勇平 ，吴 毅

（1.中南林业科技大学，湖南 长沙 410004；2.中国林业科学研究院 a.森林生态环境与保护研究所；b.资源信息研究所，北京 100091）

基于树高-年龄分级的杉木人工林多形立地指数曲线模型研究

朱光玉1，2a，2b，康 立1，何海梅1，吕 勇1，银勇平1，吴 毅1

（1.中南林业科技大学，湖南 长沙 410004；2.中国林业科学研究院 a.森林生态环境与保护研究所；b.资源信息研究所，北京 100091）

考虑相同或者相近年龄的杉木纯林，其优势木高生长受立地条件的影响较大，对年龄、优势高进行分级，基于树高-年龄分级构造哑变量，采用基于哑变量的非线性回归分析，建立区域性杉木多形立地指数曲线模型，为区域性立地质量评价和生产力预估提供研究思路和方法；同时提出一种合理的构建树高-年龄分级哑变量的思路和方法，并进一步研究分级哑变量如何加在模型参数上较为合理。以湖南不同地区606组杉木纯林优势木平均高-年龄数据为研究对象，采用理查德等4种常用非线性方程进行模拟与分析，找出最优基础模型。采用循环迭代法结合最优基础模型，对树高和年龄进行分级，找出最佳的分级结果并构建哑变量：(1)先给定初始龄阶间距值3年，对各龄阶树高进行20种分级方法，得到不同树高分级方法所对应的哑变量，采用含哑变量的非线性回归分析方法进行树高-年龄相关关系模拟，并分析、对比建模精度与效果，找出最优的树高分级方法及结果；(2)基于最优树高分级结果，考虑17种不同的龄阶划分方法，得到17种不同龄阶所对应的哑变量，采用含哑变量的非线性回归方程模拟树高-年龄相关关系，并分析、对比建模精度与效果，找出最优的龄阶划分方法及结果；(3)基于(2)中最优龄阶，重复1)的研究工作，得到最优的树高分级结果及所对应的哑变量，即最优哑变量。基于最优哑变量，考虑到哑变量加在不同的参数上模型模拟预测效果可能不一致，采用7种不同加哑变量的方法，进行树高-年龄生长曲线模拟，并对比、分析其模拟效果，模型检验采用确定系数(R2)、绝对平均误差(MAE)、均方根误差(RMSE)和残差4个指标，找出最优模型，并绘制多形立地指数曲线图。通过对4种非线性模型的建模精度分析与比较得到理查德方程最优，模型表达式为：H=a×[1-exp(-b×Age)]c，其确定系数(R2)为0.799 644；基于最优模型，采用含哑变量的非线性回归分析，利用循环迭代法分析不同树高、年龄分级的模型模拟精度与结果，指出龄阶间距为5、树高分9级所得哑变量最优；基于最优哑变量，考虑7种哑变量模型模拟方法，得到哑变量加在参数a、b上最优，其确定系数(R2)、绝对平均误差(MAE)、均方根误差(RMSE)分别为：0.953 029、0.836 93、1.119 938，残差值均匀分布在横轴(预测值)两侧，表明模型模拟效果较好。本研究采用含哑变量的回归分析与循环迭代法，系统的构建了湖南杉木多形立地指数曲线模型，不仅明显提高了模型的精度：确定系数从0.799 644增加到0.953 029，而且为区域性立地质量评价和生产力预估模型的构建提供了可行思路和方法。

杉木人工林；树高-年龄分级；多形立地指数模型；非线性回归；哑变量

立地指数的概念最早产生于18世纪，并被作为评价立地生产潜力的指标，即利用林分中平均优势高和年龄的关系，以基准年龄时的优势高作为衡量立地生产潜力的指标[1-3]。立地指数模型的建立研究是评价森林立地质量的核心和关键。目前，国内外学者广泛采用立地指数法评价纯林立地质量[4-6]。立地指数曲线模型可分为同形（单形）和多形两种，利用同形立地指数模型进行小范围内、单一树种间的立地质量评价时可得到较好的模拟结果，但应用到大区域甚至全国范围内时效果并不理想[7]。基于此科学问题，多形立地指数曲线模型的研究成为一种趋势[8]。Bull利用多形曲线评价了红松林立地质量[9]；Carmean等在加拿大安大略省西北部建立了黑云杉和美国山杨多形立地指数模型[10]；Cieszewski等利用147块样地970组黑松数据建立了黑松多形立地指数模型，大幅提高了模型的精度和适用范围[11]；Jerez-Rico M等基于柚木临时样地和固定样地数据，研究了基于非线性混合效应的柚木立地指数模型，在委内瑞拉西部平原取得较好的效果[12]。国内，李希菲等将哑变量的回归分析方法用于多形立地指数曲线构建[13]；段爱国等以多期固定样地数据为基础，采用差分方程法构建了杉木人工林优势高生长模型，并探讨了多形立地指数模型的构建[14]。目前，关于立地指数曲线参数的求解主要有2种思路：一是利用差分方程法求解，其对数据要求比较严格，要求对固定样地进行多期观测，对于区域性立地质量评价，需要大量的财力、物力；另一种是采用经验或者理论方程，利用回归分析方法直接进行参数求解，此方法与差分方程法相比，不仅数据要求没那么严格，而且有大量成熟的统计软件可以借助，简单易行。

含哑变量的回归分析与考虑混合效应模型的回归分析，被证明对于多形立地指数曲线模型的构建是切实可行的，均是有效的[15]。但是对于区域性立地质量评价与生产力预估，关于哑变量或混合效应变量的构建与划分方法、以及哑变量或混合效应变量在模型中如何表达仍需进一步探索。

李海奎等在构建全国主要树种的树高-胸径曲线模型时，先对树高和胸径的分级得到哑变量，然后建立了含哑变量的树高-胸径曲线模型，取得了良好的效果，但是对于适宜哑变量的分级方法以及哑变量在模型中如何表达比较合理，并没有进行深入研究[16]。

第八次全国森林资源清查结果显示，我国森林每公顷蓄积量为89.79 m3，远远低于欧美发达国家水平。我国森林质量不高已成为影响林业发展的一个突出问题，未能做到“适地适树”和依据立地条件开展森林经营与培育是一个重要原因。因此，开展区域性森林立地质量评价和生产力预估研究，为区域性森林经营与培育提供基础理论依据和支持，迫在眉睫。

基于上述现实与科学问题，本研究以湖南26个地区的杉木纯林优势木平均高和年龄配对数据，开展含哑变量的多形立地指数曲线模型研究，为区域性森林立地质量评价提供基础理论研究。

1 材料与方法

1.1 数据来源

以湖南杉木纯林为对象，研究数据包括两种类型：解析木和标准地（固定样地和临时样地）数据，覆盖湘东、南、西、北和湘中地区。其中：解析木数据采集于湖南衡阳县岣嵝峰林场、湖南衡东县紫金山和四方山林场；标准地数据取自于湖南江华、双排、汝城、通道、隆回、湘乡、怀化、武冈、会同、龙山、新邵、株洲、黔阳、衡东、攸县、临湘、江永、城步、靖州、资兴、泸溪县、绥宁、桃源、新邵等26县。建模样本数据共计606组。建模样本的平均优势木年龄（Age）、和树高（H）分布情况见表1。

表1 建模样本统计Table 1 Summary statistics for modeling

1.2 研究方法

1.2.1 基础模型选择

采用4种常用的立地指数曲线模型[2-5]，对杉木优势木高和年龄的相关关系进行模拟，模型表达式列于表2，其中：H为优势木高、Age为年龄；a、b、c为待求模型参数。对模型模拟结果进行分析对比，选出最优模型。模型拟合效果评价采用确定系数（R2）、平均绝对误差（MAE）和均方根误差（RMSE）3个指标，选择确定系数最大、平均绝对误差和均方根误差最小的模型作为基础模型。

表2 4种树高-年龄曲线模型Table 2 Four kinds of height-age models

1.2.2 哑变量分级及最优哑变量的划分

由于树高受立地条件影响较大，从而导致相同或者相近年龄的树木在不同的立地条件下树高差别很大，基于此，对年龄进行等级划分（龄阶），同时对不同龄阶的树高进行分级，构造反映不同立地条件对优势高影响的分级变量，并在构建优势高及其年龄生长曲线时，将分级变量作为哑变量进行回归分析，求解立地指数曲线模型。对树高和年龄分级时采用循环迭代法，并利用含哑变量的回归分析方法判断、比较年龄与树高分级的结果，探索、找出最佳的年龄和树高分级方法。

1.2.2.1 年龄、优势高分级哑变量构造及选优

对于建模样本，令其样本量为n（n=606），对于第i个样本，其优势高为hi，其年龄为Agei。如果分别将样本中的年龄分m（m≥1）级，优势高分为p级；则对于第i个样本，其龄阶标志为其优势高分级标志为均为整数。

由于不同树高分级数可能对模型拟合结果有不同的影响，且树高分级数过大不利于实际应用，本研究对杉木最优树高分级数进行了探索研究。在本研究中给定的树高分级数m的定义域：m为整数，最小值为2，最大值为平均分级间距接近0.5时所对应的分级数。

树高级确定后，不同立地条件下，不同的龄阶划分方法有着不同的拟合结果。在本研究中，样本年龄的最大值为49 a，所以定义龄阶间距最小值为2 a，龄阶间距最大值为50 a。由于各龄阶样本数量分布不均匀，可能会出现某个龄阶只有一个样本的情况，此时该龄阶最大树高值与最小树高值相等，分级间距为0，从而导致无法正确判断该样本的树高等级。针对这种特殊情况，本研究对于龄阶中只有一个样本的数据不参与建模，而是在建模后将该样本代入各树高等级曲线中，将该样本划分到预测值与实测值最接近的树高等级曲线。

具体算法如下：

（1）对所有Agei，按l年一个龄阶等分为m个龄阶，得到如：龄阶为5 a，则1—5 a为第一个龄阶，6—10 a为第二个龄阶，以此类推；

（3）对每个hi，计算其hoi：

（1）给定初始龄阶间距为3 a（我国杉木解析木龄阶间距通常为3 a），将平均优势木年龄按3 a一个龄阶整化为Q个龄阶；将相同龄阶的树高等分为m级，即将相同龄阶的树高最大值与树高最小值的差值等分为m级。根据上述哑变量分级方法，可得每个样本观测点的初次树高分级，1级是最低等级树高曲线。利用统计之林软件中非线性回归模块，按不同树高级划分得到的不同哑变量，进行含哑变量的非线性回归分析。基础模型以理查德模型为例：

将不同树高级划分后的哑变量DJm加到基础模型参数a上，模型变为：

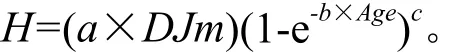
式中：a、b、c为模型参数，H为平均优势木高，Age为平均优势木年龄，DJm为树高级为m时对应的各样本树高等级。选取模拟效果最好的树高级S0级。

（2）利用哑变量分级方法，按树高级S0级，不同龄阶N年再次进行哑变量划分，可以得到不同的哑变量分级结果。

利用统计之林软件中非线性回归模块，按不同龄阶划分得到的不同哑变量结果，进行回归分析，将不同龄阶划分得到的哑变量DJN加到基础模型式参数a中，模型变为：

式中：a、b、c为模型参数，H为优势木平均高，Age为平均优势木年龄，DJN为龄阶N年时对应的各样本树高等级。选取模拟效果最好的龄阶间距K年。

（3）确定龄阶间距为K0年后，重复（1）的工作，选出最优树高级值S1。

（4）以树高分级级数S1为基础，继续对龄阶间距进行划分，选出最优的龄阶间距为K1。

（5）重复(3)和(4)，直至龄阶间距K0=K1，为常数，树高分级级数，S1=S0，为常数，则终止循环，得到最优的哑变量划分结果，其龄阶间距为K1，其树高分级级数为S1，所对应树高-年龄分级哑变量为最优哑变量，最优哑变量的级数与S1一致。

1.2.2.2 最优哑变量模型选择

为了进一步研究哑变量如何加在参数上较为合理，按照龄阶K年、树高级值S0级的哑变量划分结果，将哑变量DJ分别加在基础模型的不同参数上，进行7种情况的建模分析与比较，通过对模型进行建模精度检验，选出最优哑变量模型。7种模型的表达式如下：

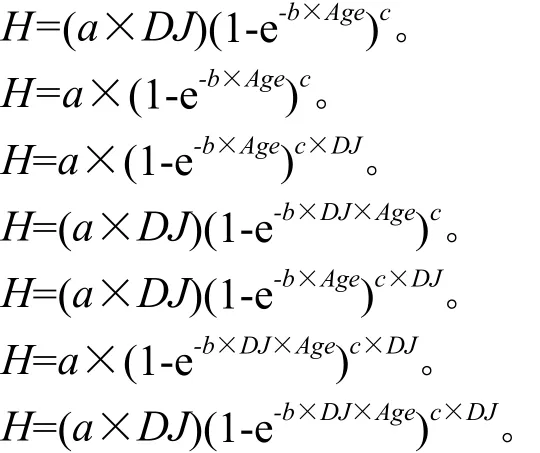
1.2.3 模型检验

模型检验采用确定系数（R2）、平均绝对误差（MAE）、均方根误差（RMSE）和残差4个评价指标，判别标准为：R2越大，精度越高；MAE、RMSE越小，精度越高；残差值分布越均匀，模型拟合效果越好。计算公式如下：

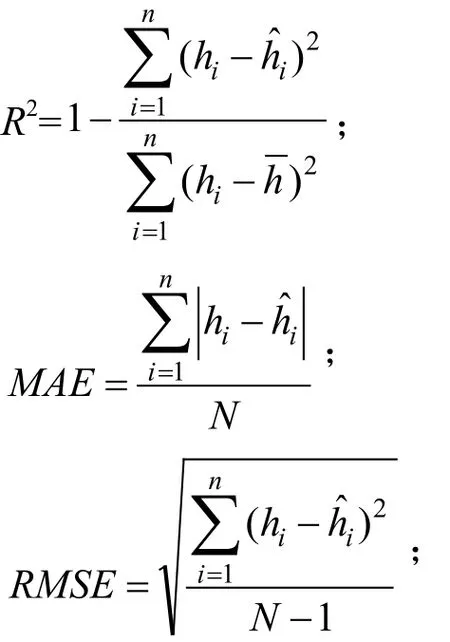
其中：hi为树高实测值，为树高预测值，为树高实测值的平均值，N为所有样本总数。

2 结果与分析

2.1 基础模型选取

利用统计之林软件中一元非线性回归模块对4种候选模型进行拟合分析，将拟合结果列于表3。结果指出理查德模型确定系数（R2）在4种候选模型中最大，为0.799 644；平均绝对误差（MAE）、均方根误差在4者中最小，分别为1.480 003、2.313 032，故选用理查德模型作为构建多形立地指数模型的基础模型。

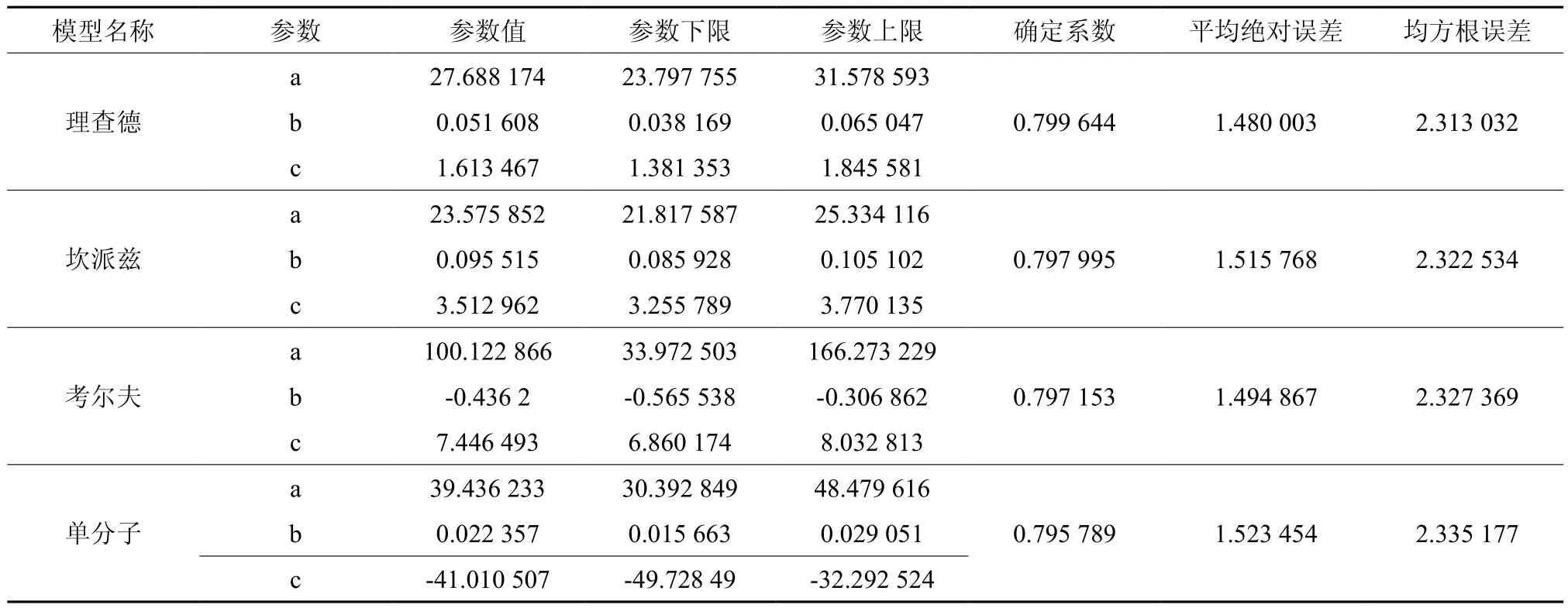
表3 4种候选模型的拟合结果Table 3 Fitting results of four candidate models

2.2 基于循环迭代法的最优哑变量的划分

（1）令初始龄阶为3 a，将平均优势木年龄按3 a一个龄阶整化为Q个龄阶；将相同龄阶的树高等分为m级，即将相同龄阶的树高最大值与树高最小值的差值等分为m级；如表4所示，树高分级数为21时，其平均分级间距为0.491，与本研究要求的精度（0.5 m 1级）是一致的，所以最低树高级值为2，最高树高级值为21，一共有20种不同的哑变量构造结果。

表4 树高级间距值Table 4 Interval value of height classification

利用统计之林软件的非线性回归模块，将20种不同的哑变量构造结果DJ，加在基础模型的参数a上分别进行拟合，建模精度检验采用MAE、RMSE和确定系数（R2）进行比较，20次拟合的精度结果如表5：

表5 不同树高分级数拟合精度Table 5 Fitting accuracy of different height classification

由各树高级值拟合结果可知：树高分9级时，其确定系数最大、MAE和RMSE的值最小，表明分9级时，模型模拟最优，所以选用9级为初始树高级。

（2）利用哑变量分级方法，按树高级9级，不同龄阶N年再次进行哑变量划分，可以得到17种不同的哑变量分级结果。

利用统计之林软件中非线性回归模块，加在基础模型的参数a上分别对17种模型进行拟合分析，拟合结果见表6。

由拟合结果可知，龄阶间距为5 a时，其确定系数最大，MAE和RMSE的值最小，模型拟合效果最好，所以初步确定龄阶间距为5 a最优。

（3）确定龄阶间距为5年后，重复（1）的研究，20次模型拟合的结果见表7。

拟合结果表明：树高级为9级时，其确定系数最大，并且其MAE和RMSE的值最小，表明其模型模拟效果最好，与（1）结果一致，所以，再次确定树高分9级最优，再基于最优树高级数划分龄阶，将得到（2）的龄阶划分结果。至此，已选出最优龄阶间距为5 a，最优树高分级级数为9级。

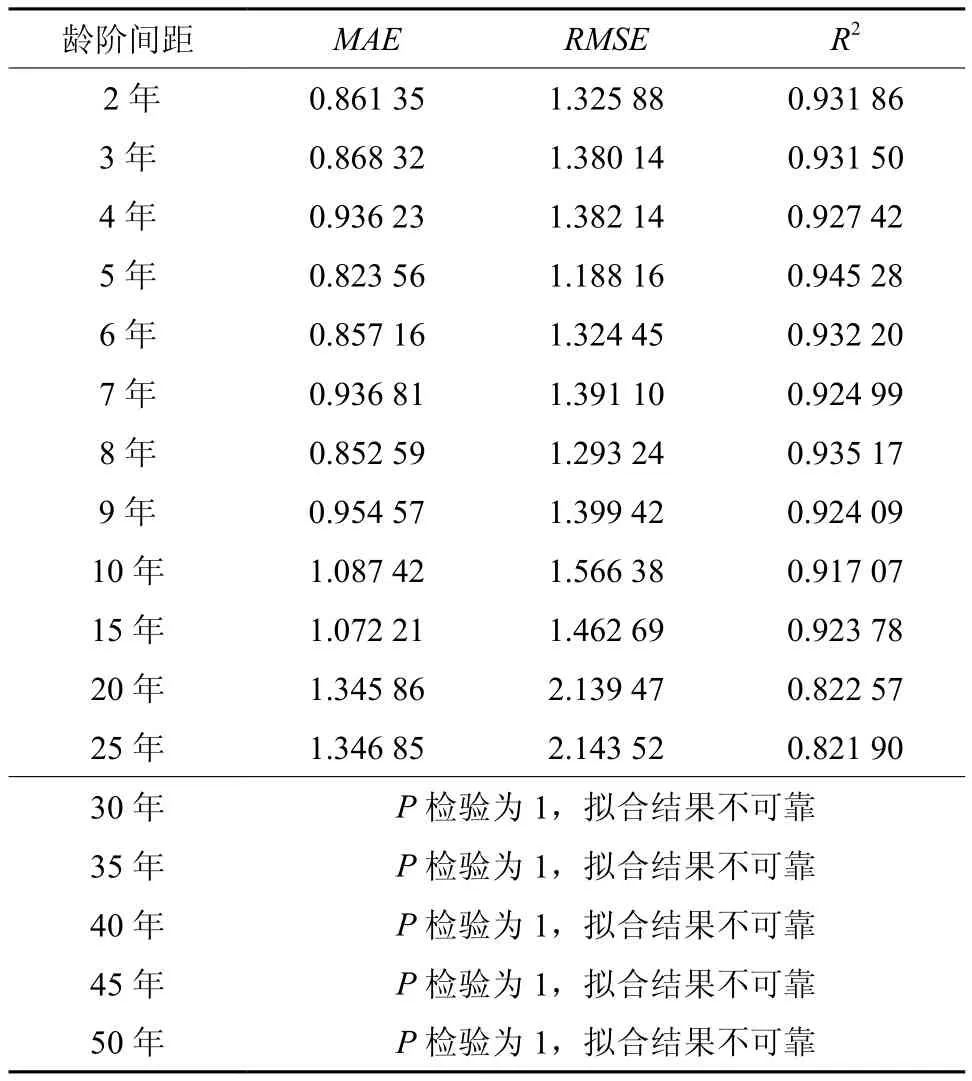
表6 不同龄阶拟合精度Table 6 Fitting accuracy of different age class

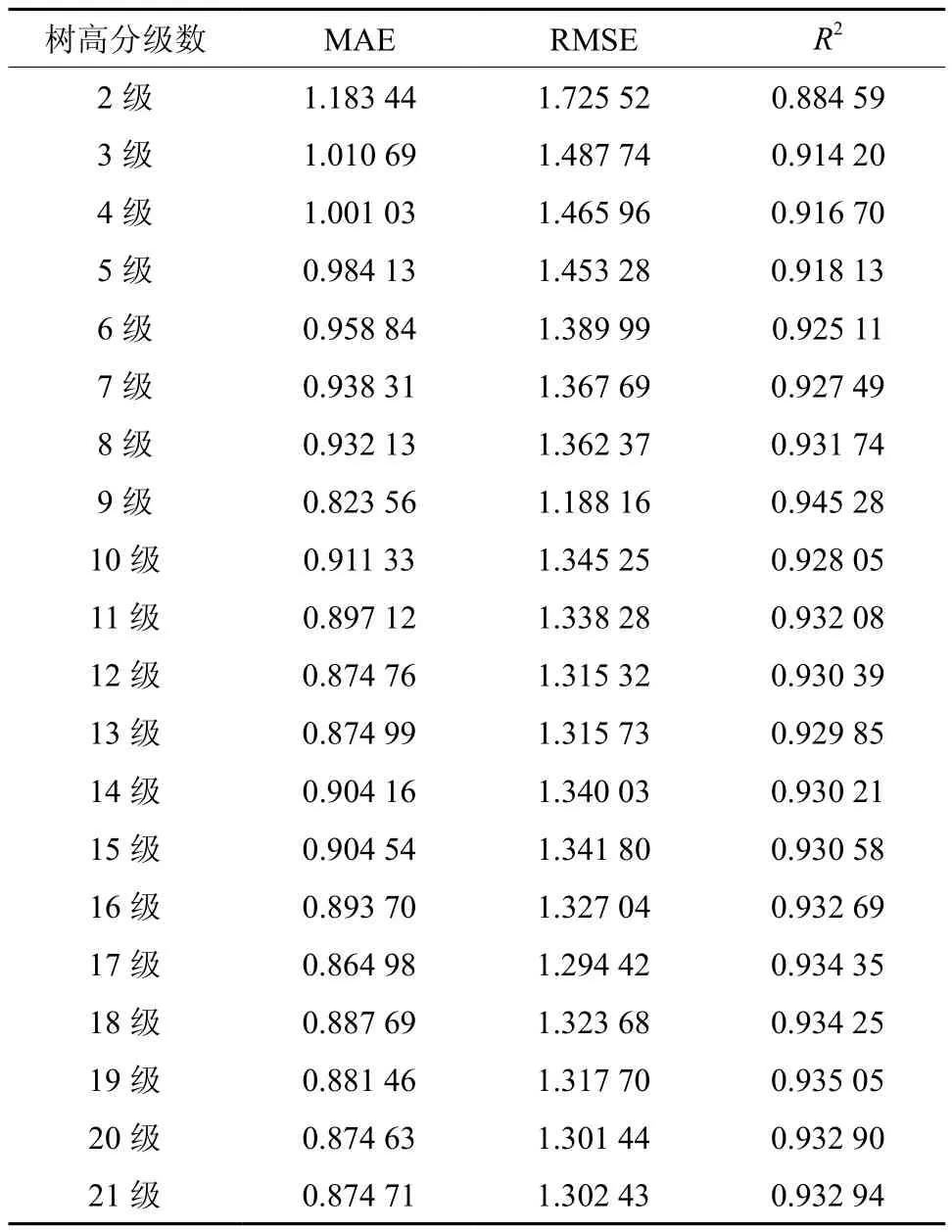
表7 不同树高分级数拟合精度Table 7 Fitting accuracy of different height classification

通过循环迭代的年龄树高分级和回归模拟比较分析可知：龄阶间距为5 a、树高分9级所构造的哑变量DJ最优。

2.3 最优含哑变量模型的选取与多形立地指数曲线模型构建

考虑到分级哑变量加在模型的不同参数上，对模型模拟效果可能有影响，将哑变量DJ分别加在基础模型的不同参数上，利用统计之林含哑变量的非线性回归分析模块，进行了7种情况的建模分析，探索最优哑变量模型（见图1）。

（1）哑变量DJ加在参数a上

其模型表达式为：H=(a×DJ)(1-e-b×Age)c。

通过模拟，模型的确定系数(R2)为0.945 278，平均绝对误差（MAE）为0.861 106，均方根误差（RMSE）为1.178 589，拟合结果见表8。

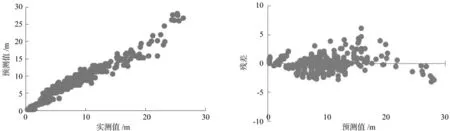
图1 哑变量DJ加在a上模型的树高实测值-预测值与预测值-残差Fig.1 Observed value-predicted value and predicted value-residuals of add dummy variable to parameter a

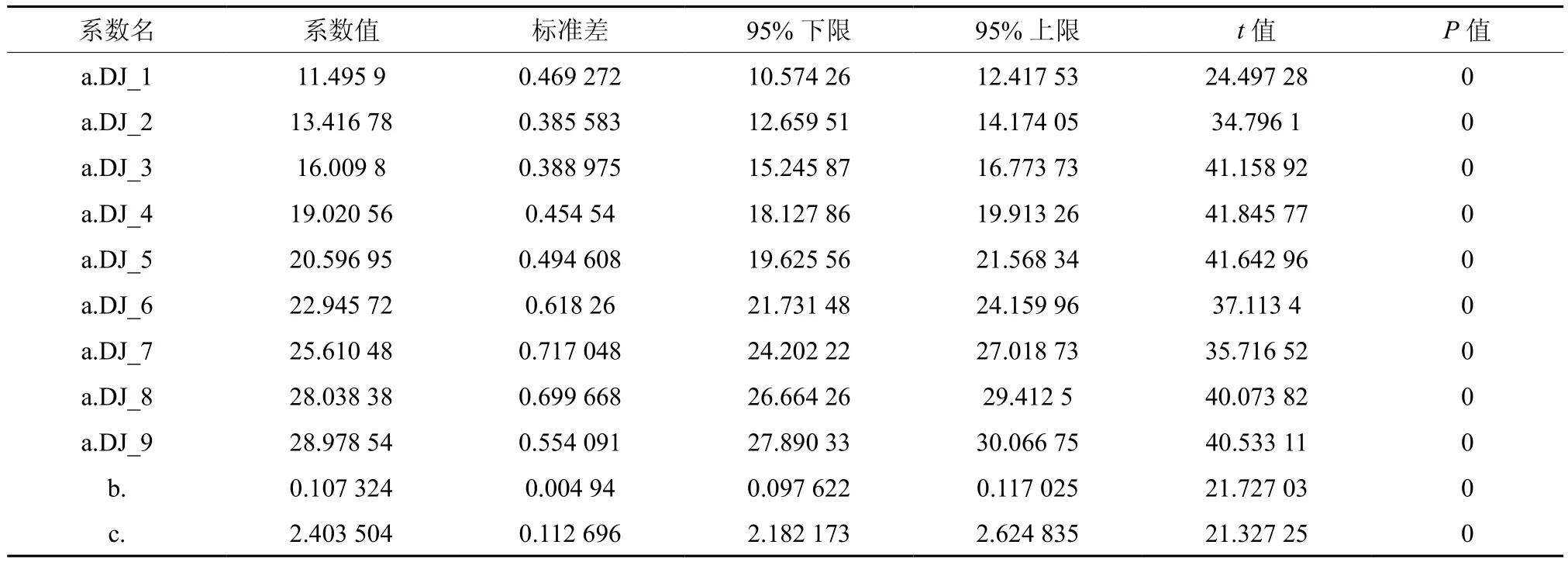
表8 哑变量加在参数a上的模型模拟参数Table 8 Model Simulation parameters with adding dummy variable to parameter a

（2）哑变量DJ加在参数b上

其模型表达式为：H=(a×DJ)(1-e-b×DJ×Age)c。

通过拟合可得，模型参数a的拟合检验值P值等于1，表明参数a的拟合没有达到预期，结果不可信（见表9）。

（3）哑变量DJ加在参数c上

其模型表达式为：H=(a×DJ)(1-e-b×Age)c×DJ。

通过拟合得，模型的确定系数（R2）为0.924 894，平均绝对误差（MAE）为1.041 839，均方根误差（RMSE）为1.416 174，拟合结果见表10和图2。

（4）哑变量DJ加在参数a、b上：

其模型表达式为：H=(a×DJ)(1-e-b×DJ×Age)c。

通过模型拟合，模型的确定系数（R2）为0.953 029，平均绝对误差（MAE）为0.836 93，均方根误差（RMSE）为1.119 938，拟合结果见表11和图3。

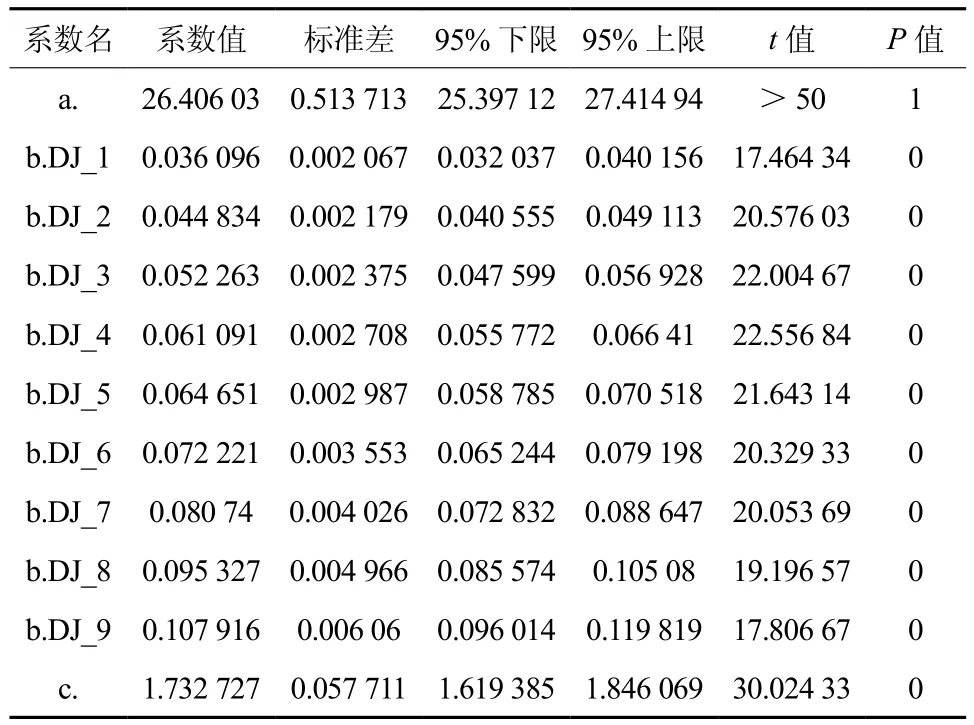
表9 哑变量加在参数b上的模型模拟参数Table 9 Model simulation parameters with adding dummy variable to parameter b

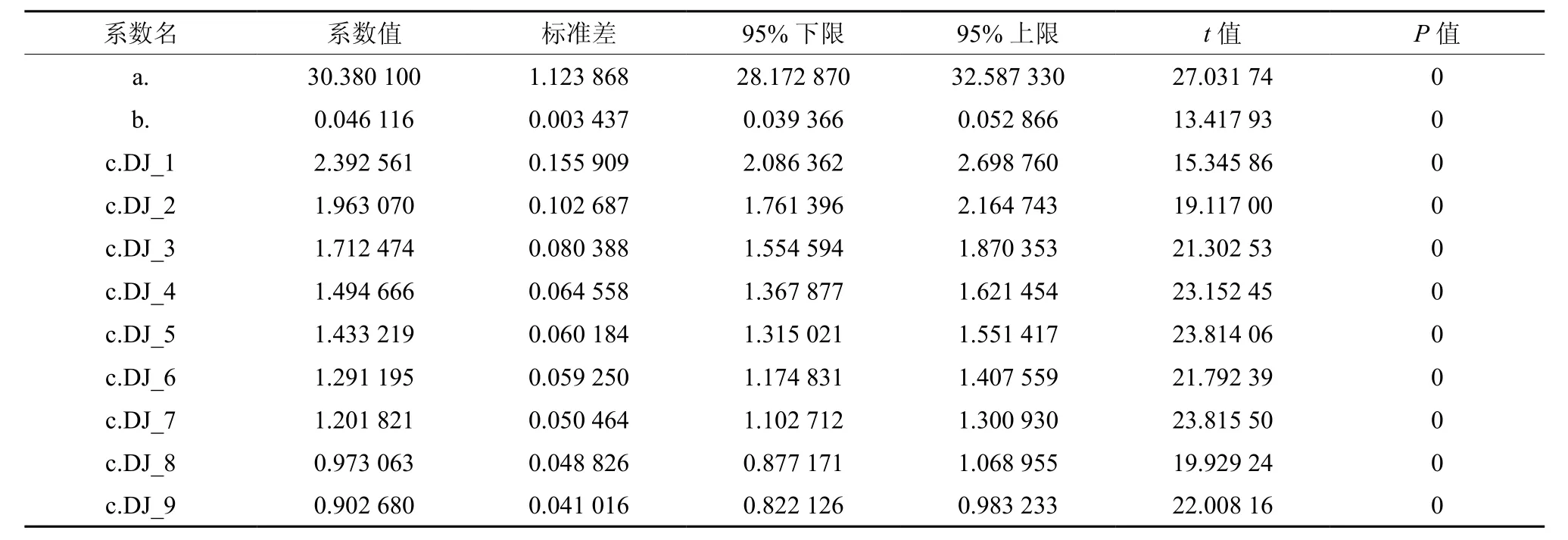
表10 哑变量加在参数c上的模型模拟参数Table 10 Model simulation parameters with adding dummy variable to parameter c

图2 哑变量DJ加在参数c上模型的树高实测值-预测值与预测值-残差Fig.2 Observed value--predicted value and predicted value-residuals of add dummy variable to parameter c

（5）哑变量DJ加在参数b、c上

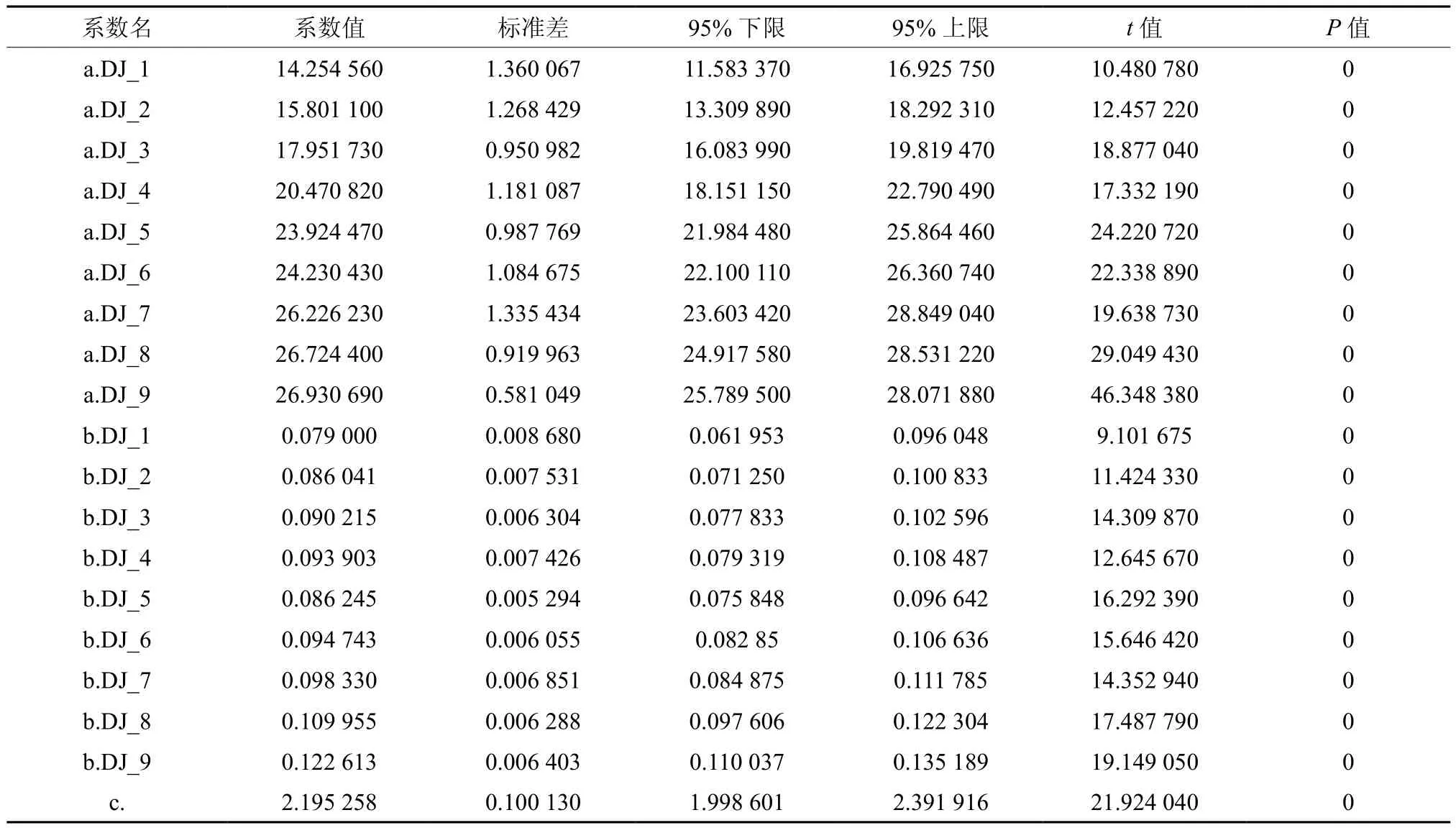
表11 哑变量加在参数a、b上的模型模拟参数Table 11 Model simulation parameters with adding dummy variable to parameters a and b

图3 哑变量DJ加在参数a、b上模型的树高实测值-预测值与预测值-残差Fig.3 Observed value-predicted value and predicted value-residuals of add dummy variable to parameters a, b

其模型表达式为：H=(a×DJ)(1-e-b×DJ×Age)c×DJ。

通过拟合可得，模型参数a的拟合检验值P值等于1，表明参数a的拟合没有达到预期，结果不可信（见表12）。

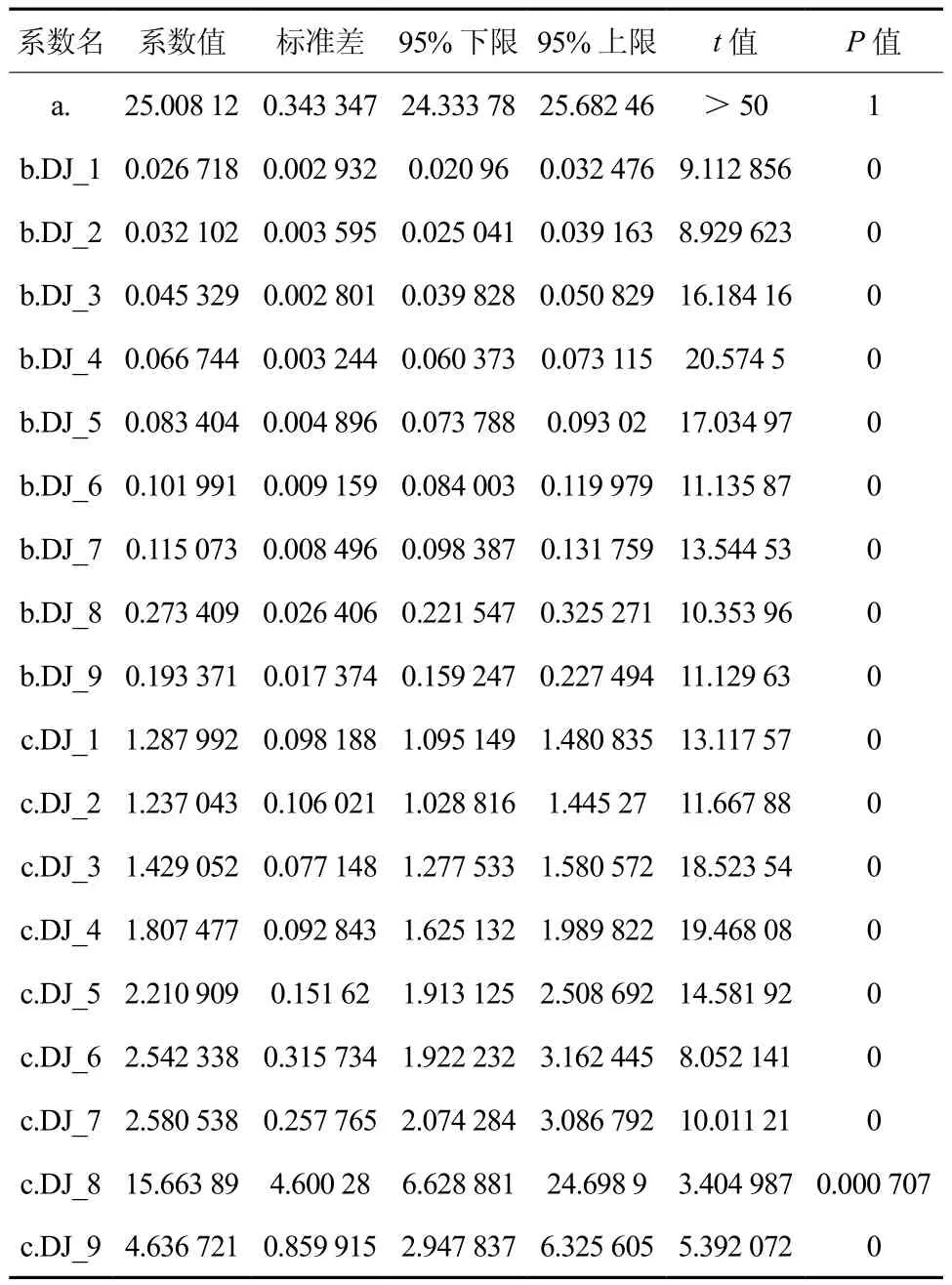
表12 哑变量加在参数b、c上的模型模拟参数Table 12 Model simulation parameters with adding dummy variable to parameters b and c

（6）哑变量DJ加在参数a、c上

其模型表达式为：H=(a×DJ)(1-e-b×Age)c×DJ。

通过模型拟合，模型的确定系数（R2）为0.949 347，平均绝对误差MAE为0.839 631，均方根误差RMSE为1.139 34。参数估计和预测值分布情况见表13。

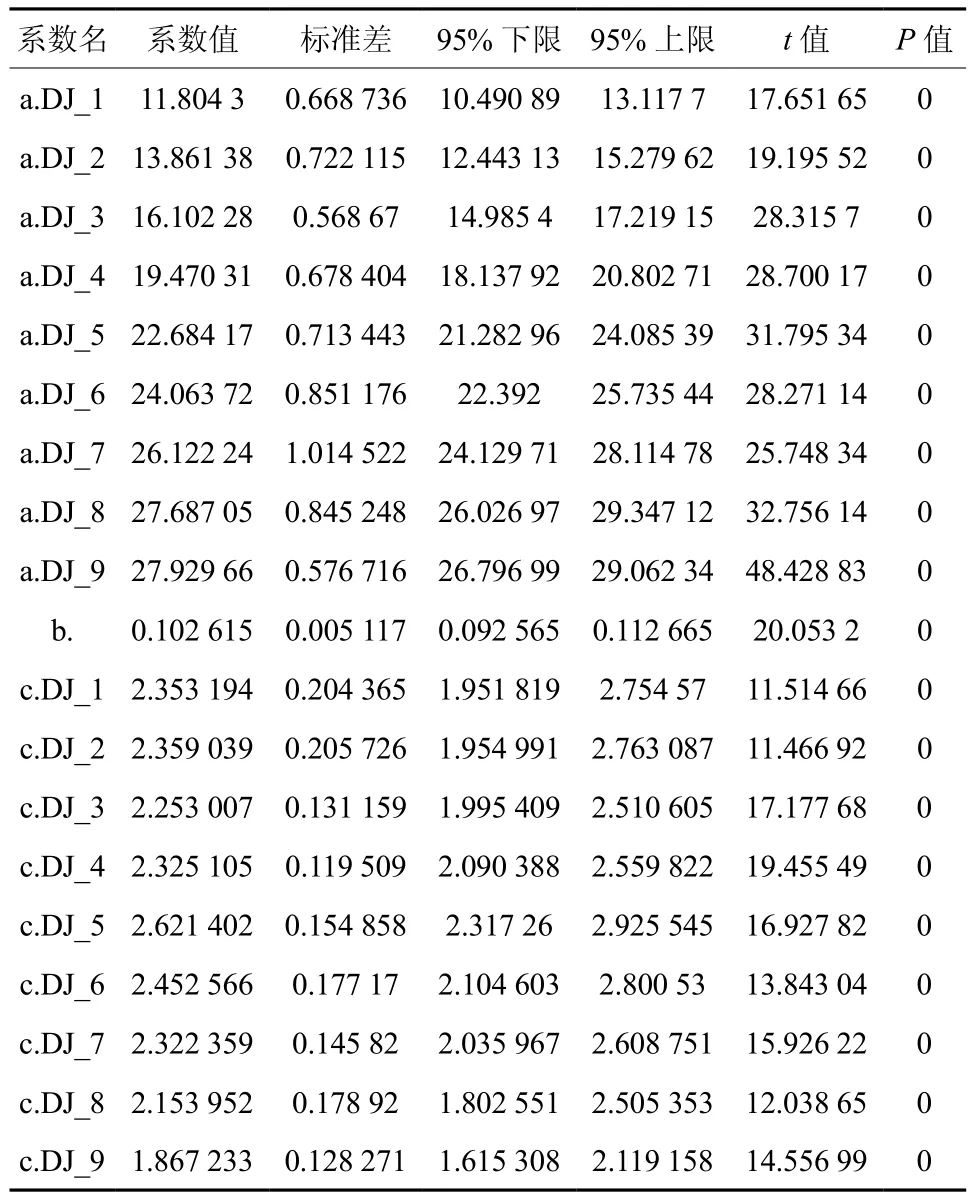
表13 哑变量加在参数a、c的模型模拟参数Table 13 Model simulation parameters with adding dummy variable to parameters a and c

（7）哑变量DJ加在参数a、b、c上

其模型表达式为：H=(a×DJ)(1-e-b×DJ×Age)c。

通过拟合可得，模型参数a的第9个等级的拟合检验值P值等于1，表明参数a的拟合没有达到预期，结果不可信（见表14）。

（8）最优哑变量模型选取

分别在不同参数上添加哑变量，利用统计之林中的非线性回归模块进行7次不同的拟合分析。从确定系数、平均绝对误差、均方根误差、树高实测值-预测值和树高预测值来看，在参数a、b上添加哑变量结果最优，所以最优哑变量模型为：H=(a×DJ)(1-e-b×DJ×Age)c。

（9）多形立地指数曲线模拟与分析

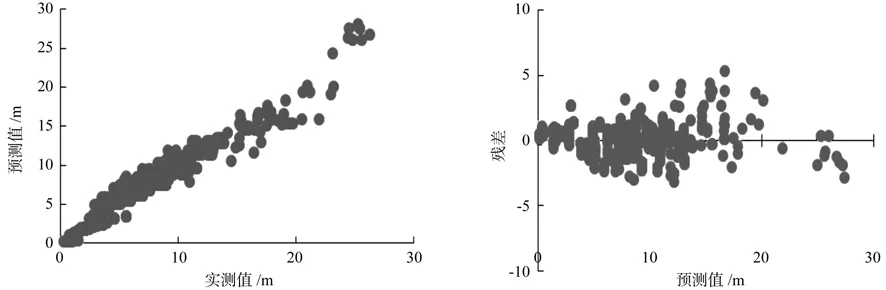
图4 哑变量DJ加在参数a、c上模型的树高实测值-预测值与预测值-残差Fig.4 Observed value-predicted value and predicted value - residuals of add dummy variable to parameters a, c

表14 哑变量加在参数a、b、c上的模型模拟参数Table 14 Model simulation parameters with adding dummy variable to parameters a, b and c

利用最优模型 H=(a×DJ)(1-e-b×DJ×Age)c，模拟研究区杉木平均优势木树高和年龄的相关关系，参数预估值见表12， 模型的确定系数（R2）为0.953 029，平均绝对误差（MAE）为0.836 93，均方根误差（RMSE）为1.119 938。基于此导向曲线绘制其立地质量预估效果图，即多形立地指数曲线图，图5中的散点表示观测值，即建模用数据。

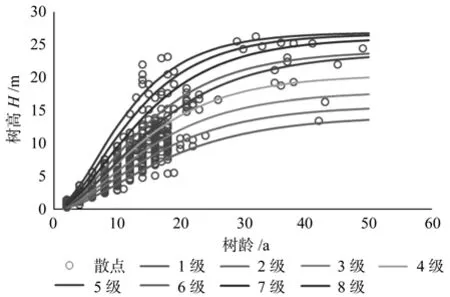
图5 多形立地指数曲线Fig.5 Polymorphic site index curve

各立地质量等级对应的树高-年龄散点图如图6。

通过各立地等级对应的树高-年龄散点图，可知各个立地等级的立地指数曲线模拟效果均较好，体现了模型精度较高的特点，进一步证实了模型的可行性和适用性，同时也验证了哑变量划分与选择的合理性与可行性；哑变量级数值越高，优势木生长越好，立地条件越好，立地质量越高。

3 结 论

本研究以湖南东、南、西、北、中26个县的杉木人工纯林为对象，收集包括固定样地、临时样地和解析木等606组样品，采用循环迭代的思维和含哑变量的非线性回归分析方法，构建了湖南杉木人工林多形立地指数曲线模型。

采用理查德（Richards）、坎派兹（Gompertz）、考尔夫（Korf）和单分子（Mitscherlich）4种非线性模型对优势木高和年龄的相关关系进行模拟，选出最优模型为理查德（Richards）函数：H=a×[1-exp(-b×Age)]c。

图6 9种树高-年龄分级曲线Fig.6 Nine kinds of curve with classi fi cation of height and age

考虑到不同条件下杉木生产潜力的差异性，首次采用循环迭代的思维对平均优势木的年龄和树高进行等级划分，借助含哑变量的非线性回归进行分级结果检验，指出年龄分级时，龄阶间距为5年，树高分9级，其所得的分级哑变量最佳，分级最佳哑变量即为杉木立地质量高低定性划分的依据，分级哑变量的等级值越大，优势木生长越好，立地质量越好。

考虑树高-年龄分级哑变量对理查德（Richards）生长方程3个参数的影响可能不一致，采用了哑变量分别加在不同参数上的7种情况进行了7种含哑变量的非线性回归模型模拟，并利用模型的确定系数（R2）、平均绝对误差（MAE）、均方根误差（RMSE）等，来比较分析不同模型的精度，指出最优模型为：H=(a×DJ)(1-e-b×DJ×Age)c。并绘制了该模型的多形立地指数曲线图，及分9级的各级曲线图，图示表明模型模拟效果较好。与基础模型相比，将模型的确定系数从0.799 644增至0.953 029，大大提高了模型的精度。同时也验证了树高-年龄分级的方法是正确、可行的。

研究结果为区域性立地指数曲线的构建提供一种新思路，有助于区域性立地质量评价。

[1]Nanos N, Calama R, Cañadas N, et al. Spatial stochastic modelling of cone production from stone pine (Pinus pinea L.)stands in the Spanish Northern Plateau[C]// Modelling forest systems. Workshop on the interface between reality, modelling and the parameter estimation processes, Sesimbra, Portugal, 2-5 June 2002.

[2]Payandeh B, Wang Y. Relative accuracy of a new base-age invariant site index model[J]. Forest Science, 1994, 40(2):341-348.

[3]Harry Eriksson, Ulf Johansson, Andres Kiviste. A site-index model for pure and mixed stands of Betula pendula and Betula pubescens in Sweden[J]. Scandinavian Journal of Forest Research, 1997, 12(2):149-156.

[4]Yue C, Mäkinen H, Klädtke J, et al. An approach to assessing site index changes of Norway spruce based on spatially and temporally disjunct measurement series[J]. Forest Ecology &Management, 2014, 323(7):10-19.

[5]Batho A, García O. A Site Index Model for Lodgepole Pine in British Columbia[J]. Forest Science, 2014(2): 60.

[6]Kimberley M O, Ledgard N J. Site index curves for Pinus nigra grown in the South Island high country, New Zealand[J]. New Zealand Journal of Forestry Science, 1998(1): 389-399.

[7]Devan J S, Burkhart H E. Polymorphic site index equations for loblolly pine based on a segmented polynomial differential model[J]. Forest Science, 1982, 28(3):544-555.

[8]陈绍玲. 马尾松人工林多形地位指数曲线模型的建模方法[J].中南林业科技大学学报, 2008, 28(2): 125-128.

[9]Bull H. The use of polymorphic curves in determining site quality in young red pine plantations[M]. US Government Printing Of fi ce, 1931.

[10]Carmean W H, Hazenberg G, Deschamps K C. Polymorphic site index curves for black spruce and trembling aspen in northwest Ontario[J]. Forestry Chronicle, 2006, 82(2): 231-242.

[11]Cieszewski C J, Bella I E. Polymorphic height and site index curves for lodgepole pine in Alberta[J]. Canadian Journal of Forest Research, 2011, 19(9): 1151-1160.

[12]Jerez-Rico M, Moret-Barillas A Y, Carrero-Gámez O E, et al. Site index curves based on mixed models for teak (Tectona grandis L. F.) plantations in the Venezuelan plains[J]. Agrociencia, 2011,45(1):135-145.

[13]李希菲,洪玲霞.用哑变量法求算立地指数曲线族的研究[J].林业科学研究, 1997,10(2):108-112.

[14]段爱国,张建国.杉木人工林优势高生长模拟及多形地位指数方程[J]. 林业科学, 2004,40(6):13-19.

[15]Palahí M, Tomé M, Pukkala T, et al. Site index model for Pinus sylvestris in north-east Spain[J]. Forest Ecology & Management,2004, 187(1):35-47.

[16 李海奎,法 蕾.基于分级的全国主要树种树高-胸径曲线模型[J].林业科学, 2011,47(10):83-90.

Study on polymorphic site index curve model based on height-age classi fi cation for Cunninghamia lanceolata plantation

ZHU Guangyu1,2a,2b, KANG Li1, HE Haimei1, LV Yong1, YIN Yongping1, WU Yi1
(1.College of Forestry, Central South University of Forestry and Technology, Changsha 410004, Hunan, China; 2a. Institute of Forest Ecology, Environment and Protection; 2b. Research Institute of Forestry Resource Information Techniques, Chinese Academy of Forestry, Beijing 100091, China)

In this study, the tree age and its dominant height of Cunninghamia lanceolata plantation are fi rstly classi fi ed in consideration of the pure stands of Cunninghamia lanceolata in the same or similar age whose growth of dominant tree is greatly affected by site conditions. Secondly, the dummy variable will be constructed on the basis of classification of tree height and age, Finally, the polymorphic site index curve model for regional Cunninghamia lanceolata will be established, employing the non-linear regression analysis based on the dummy variable. The above research will provide new ideas and methods for evaluating forest site quality and estimating productivity in regional forest. In the same time, a new reasonable method of constructing dummy variables of tree height and age classi fi cation is also proposed and how to reasonably add the dummy variable to the model will be further studied in the research. In this study,the data of average height and age of dominant tree is taken as the study subject, which are from 606 groups of Cunninghamia lanceolata pure forest in different regions of Hunan province. In order to fi nd the optimal basic model, the commonly used nonlinear equations as Richards, Gompertz, Korf and Mitscherlich are employed to simulate and analyze. In the purpose of fi nding out the ideal results of classi fi cation to construct the dummy variables, the cyclic iterative method integrated with the optimal basic model is taken to classify the tree height and age. The speci fi c implementation steps are as follows: Firstly, setting the three-year as the initial tree age graduation, classifying the tree height of various age graduation by nine methods, then the corresponding dummy variables to different trees’ classi fi cation methods will be obtained, employing non-linear regression analysis method with the dummy variables to simulate and analyze the relationship between tree height and tree age, comparing the accuracy and validity of models to fi nd out the optimal classifying method and the ideal result of tree height. Secondly, 17 kinds of different tree age classi fi cation methods and their corresponding dummy variables are obtained from the above ideal result, employing non-linear regression analysis method with the dummy variables to simulate and analyze the relationship between tree height and tree age, comparing the accuracy and validity of models to fi nd out the optimal classifying method and the ideal result of tree-age graduation. Thirdly, the optimal corresponding dummy variable and tree-height classi fi cation are obtained from the above optimal tree-age graduation by repeating the fi rst step. Based on the optimal dummy variable, the growth curve of the tree height and age is simulated by taking seven different methods with the dummy variable in consideration of that adding the dummy variable to different parameters’ model to simulate would obtain different results.And then comparing and analyzing these simulation effects to fi nd out the optimal model to draw the polymorphic site index curve. The model is tested by the following four indexes as the determine coef fi cient(R2), mean absolute error(MAE), root mean square error(RMSE)and the residual error. The fi rst one is that the Richard equation is the optimal one by comparing and analyzing the modeling accuracy of the four kinds of non-linear models, and its expression is ,whose determinant parameter R2 is 0.79964,And the second one is that the optimal dummy variable is obtained when the tree-age graduation set as fi ve-year and the tree-height classi fi ed into nine classi fi cations by adopting the non-linear regression with dummy variables and employing the cyclic iterative methods to analyze the model simulation accuracy and validity of different tree height classi fi cation and tree age graduation on the basis of the optimal model. And the third one is that the dummy variable added to the parameters of a、b is the optimal one by simulating seven kinds of models with dummy variables on the basis of the optimal dummy variable, whose determinant coef fi cient(R2), mean absolute error(MAE), root mean square error(RMSE)are 0.953 029、0.836 93、1.119 938 respectively, and the residual values evenly distribute on both sides of the horizontal axis, which shows that the validity of the model is good. In this study, the polymorphic site index curve model for Cunninghamia lanceolata of Hunan province is systematically established by employing the methods of regression analysis with dummy variables and cyclic iteration method,which not only increased the accuracy of determinant coef fi cients from 0.799 644 to 0.953 029, but also provide new ideas and methods for constructing the model of evaluating forest site quality and estimating productivity prediction in regional places.

Cunninghamia lanceolata plantation; height-age classi fi cation; polymorphic site index model; nonlinear regression; dummy variable

S757.2

A

1673-923X(2017)07-0018-12

10.14067/j.cnki.1673-923x.2017.07.003

2016-07-03

国家自然科学基金（31570631，31100476）；国家林业局项目（1692016-06，SFA2130218）；中国博士后科学基金面上项目（2014M550103）；湖南省教育厅项目（17C1664）

朱光玉，副教授，博士；E-mail：zgy1111999@163.com

朱光玉，康 立，何海梅，等.基于树高-年龄分级的杉木人工林多形立地指数曲线模型研究[J].中南林业科技大学学报，2017, 37(7): 18-29.

[本文编校：吴 毅]