三相变压器短路电抗在线检测方法研究*
苏小芳,费雯丽,刘雷,汪一雄,周兴隆
(1.湖北第二师范学院数学与经济学院,武汉430060;⒉武汉大学电气工程学院,武汉430072)
0 引 言
电力变压器是电网中的重要设备,电气变压器的安全运行对保障电力系统的正常运行有重大意义。因变压器绕组变形而导致的变压器事故占变压器总事故的绝大多数[1],所以为了能够及时发现变压器的事故隐患、延长变压器的使用寿命以及保证整个电力系统的安全稳定运行,对变压器绕组变形检测方法的研究具有十分重要的意义[2-4]。
现有的理论研究表明,变压器的短路电抗值是由绕组的几何尺寸、空间位置等因素所决定。当变压器绕组发生变形时,其短路电抗值将会发生变化,因此测量短路电抗变化情况是判断变压器绕组是否变形的一种有效方法[5-7]。对变压器短路阻抗的准确测量是十分重要的。
目前,基于短路阻抗法的变压器绕组变形试验方法主要有两类,一类是需要将变压器从电网断开,进行空载试验和负载试验,这是离线的;另一类在线监测方法,其数学计算模型针对的是单相双绕组实验变压器[8]。因此,这两类方法都不适用对电网中实际运行的电力变压器进行短路阻抗的在线监测。
为解决以上问题,提出一种三相变压器绕组变形短路阻抗的在线监测方法,建立了三相变压器绕组短路阻抗参数的数学计算模型,使得可以通过在线测量的方法计算三相变压器的短路阻抗,从而可以实时的判断三相变压器绕组的变形情况。同时,进行了仿真和试验研究,验证了该方法的有效性。
1 基于短路阻抗法的三相变压器绕组变形在线监测原理
由于电力系统中三相变压器的绕组连接方式通常为Y-D连接,因而本发明主要针对Y-D连接的三相变压器绕组变形在线监测方法。图1是三相变压器的等效原理图。
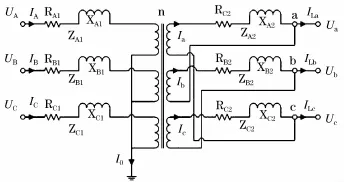
图1 三相变压器等效电路图Fig.1 Equivalent circuit diagram of three-phase transformer
A相原边短路阻抗、电阻、电抗分别为ZA1、RA1、XA1;A相副边短路阻抗、电阻、电抗分别为 ZA2、RA2、XA2。B、C相阻抗参数表示方法同理。将低压侧的短路阻抗折算到高压测,三相变压器的短路阻抗可分别表示为:
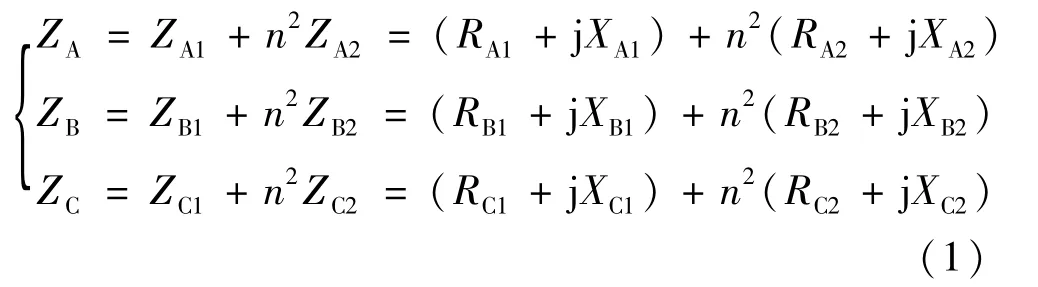

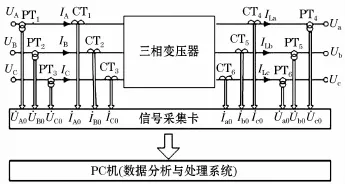
图2 三相变压器短路阻抗在线测量原理图Fig.2 Schematic diagram of three-phase transformer short-circuit impedance on-line measurement
根据基尔霍夫电压定律,可得副边相电压:

根据基尔霍夫电流定律,可得副边电流关系式:

根据基尔霍夫电流定律,可得原边电流关系式:

又根据变压器原、副边电流之间的关系,有:

根据以上三个电流表达式,可以计算得到,三相变压器副边相电流为:
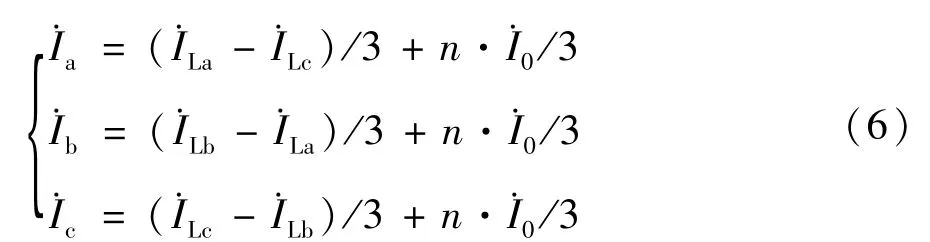
即:
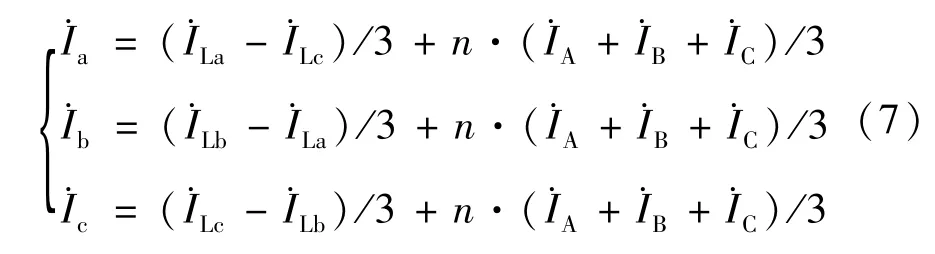
对于单相双绕组变压器,其短路阻抗为[8]:
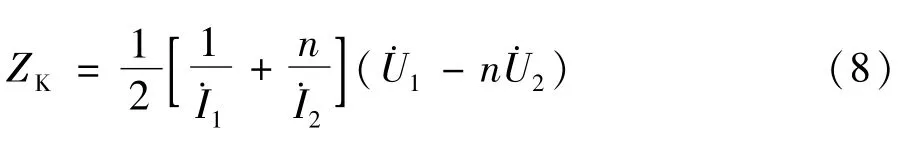

根据单相变压器的短路阻抗计算式,以及计算得到的Y-D连接的三相变压器原边、副边的相电压、相电流表达式,可得三相变压器的短路阻抗表达式:

2 误差分析
利用均值法在线计算变压器短路电抗时,其测量误差将由以下几个部分组成:
(1)原边母线和副边母线上PT的测量误差δKTV1~δKTV6。在线测量是一个稳态过程,故PT的测量误差表示的是稳态电压比的偏差;
(2)原边母线和副边母线上CT的测量误差δKTA1~δKTA6。若采用0.2级的PT和CT,在额定值附近的大多数负荷情况下,其幅值测量误差小于0.2%;
根据文献[9]中所述,随机误差合成可以采用基于标准差方和根合成的方法,同时在测量实际中,各个单项随机误差都以极限误差的形式表示,因此考虑采用极限误差的合成。
测量系统的总极限误差为:
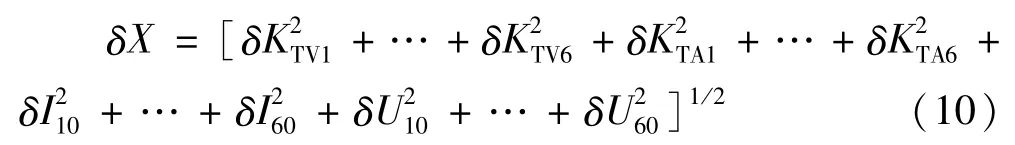
上式是在满足各单项误差服从正太分布或近似服从正太分布以及它们之间是不相关或近似不相关的条件下获得的计算公式。从实际的情况来看,各互感器误差以及采样信号的误差服从正太分布或者近似服从正太分布,同时各个单相误差不相关,所以采用等式(10)计算总的极限误差时可行的,由此可得测量系统的准确度小于0.8%。另外,在系统实际运行电流和电压信号中存在直流和谐波分量以及噪声等干扰信号,需通过数字信号分析技术予以消减;随机误差可以通过多次采集取平均值的方式加以控制,使得总误差可稳定的控制在1%以内。
3 仿真研究
以某供电公司的SZ10-40000/110大型电力变压器参数为依据,建立三相电力变压器的短路电抗在线测量的仿真模型。该变压器采用的接线方式为YNd11联结方式。仿真模型如图3所示。利用PT、CT测量变压器三相的母线电压与母线电流,以及原边零序电流。
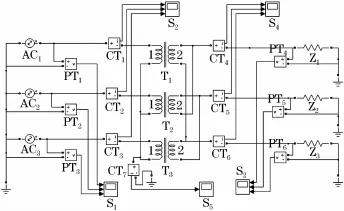
图3 仿真原理图Fig.3 Simulation schematic diagram
根据出厂试验的数据,计算得到变压器的励磁阻抗理论值为146.91+j232.55 kΩ,短路阻抗理论值为1.091 3+j33.483 7Ω。
为了使变压器仿真模型真实并考虑原副边漏电抗较为严格的实际情况,考虑以下因素:
(1)B相短路电抗与A、C相短路电抗不相等。
三相心式变压器的A、B、C三相绕组所处的空间位置并不完全对称相同,所以漏磁回路也并不相同,造成A、B、C三相的短路电抗并不相等。B相通常处于A、C相的中间,其漏磁回路应该明显区别与A、C相的漏磁回路。根据该变压器故障录波器的测试数据计算A、B、C三相的短路电抗值,发现B相的短路电抗的确比A、C相的短路电抗小(大约1Ω),并且A、C相的短路电抗也比较接近,计算结果与定性分析结果一致。
(2)变压器原副边漏电抗的标幺值比值为1:2。
实际情况,变压器原副边漏电抗的标幺值并不完全相等,因此仿真中考虑更为严格的假设条件。假设它们的比值均为1:2。
同时,为了简化变压器仿真模型,假设变压器满足以下条件:
(1)A、B、C三相的励磁阻抗相等。
对于三相心式变压器A、B、C三相的励磁回路和它的漏磁回路情况一样,长度并不相等,中间B相磁路相对较短,磁阻较小;两边A、C相磁路相对较长,磁阻较大。但励磁阻抗的不对称对于变压器运行状态的影响极小,所以假设A、B、C三相的励磁阻抗相等。
(2)A、B、C三相的原副边短路电阻值相等。
由变压器出厂试验中直流电阻值测试结果可知,A、B、C三相的原副边电阻值不平衡度极小。同时,观察发现直流电阻值的测量结果与负载试验测得的电阻值结果相差较大,前者约为0.769 5Ω,后者则约为1.091 3Ω,这是因为变压器在运行时温度会升高,造成绕组电阻值增加的缘故。该变化对于在线测量的计算误差影响极小,所以不考虑变压器绕组电阻值的变化,以负载试验测得的电阻值为准,并假设A、B、C三相的电阻值相等,同时每一相的原副边电阻值也相等。
(3)A、B、C三相的几何匝比完全相同。
(4)A、B、C三相的额定容量和额定电压相同。
因此,三个单相变压器的具体仿真参数设置如表1所示。
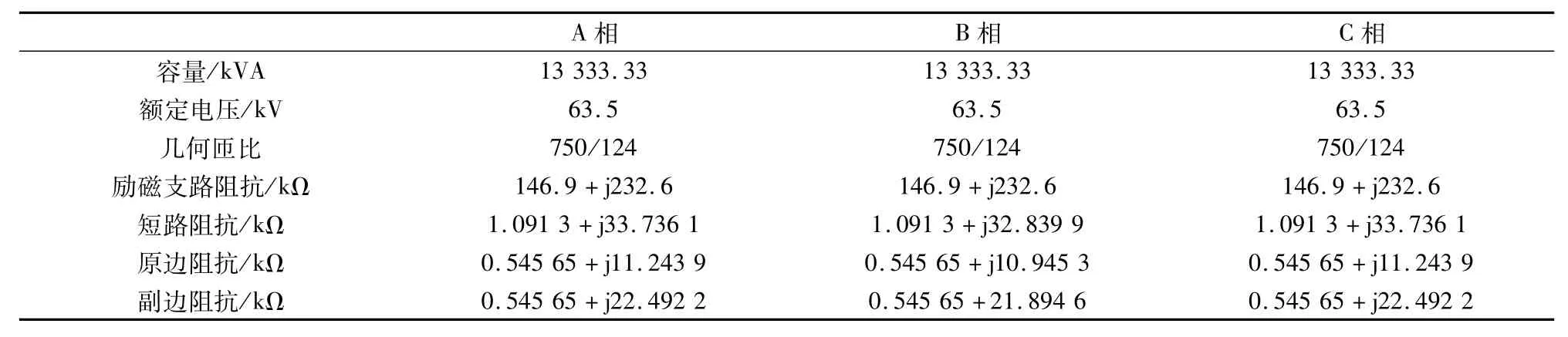
表1 各个单相变压器的仿真参数Tab.1 Simulation parameters of each single phase transformer
变压器的三相负载对称,负载率由0.53%变化至1.4%。变压器A、B、C三相短路电抗值的计算结果随负载率变化曲线如图4所示。

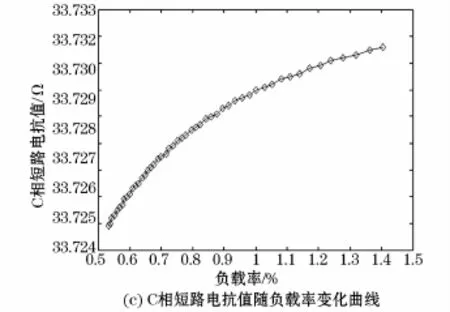
图4 三相变压器短路电抗随功率因数变化曲线Fig.4 Changing curve of short-circuit reactance of three-phase transformer with power factor variation
从图4中可以看出,变压器A、B、C三相短路电抗在线检测值随着负载率的增加而增大。A相短路电抗最大值为33.731 5Ω,最小值为33.724 6Ω,短路电抗最大变化值相对其均值为0.01%;B相短路电抗最大值为32.835 6Ω,最小值为32.829 1Ω,短路电抗最大变化值相对其均值为0.01%;C相短路电抗最大值为33.731 6Ω,最小值为33.724 9Ω,短路电抗最大变化值相对其均值为0.01%。
变压器的三相负载对称,功率因数由0.6变化至1。以均值法在线计算变压器A、B、C三相的短路电抗值,其计算结果随功率因数变化曲线分别如图5所示。
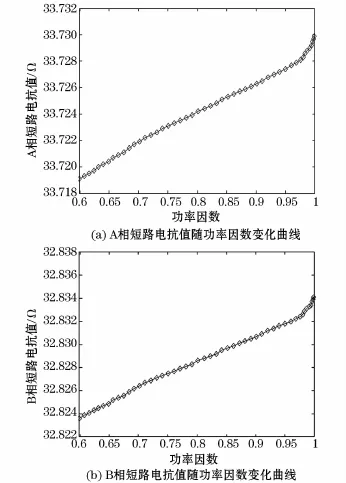
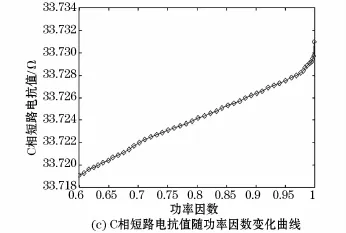
图5 三相变压器短路电抗随功率因数变化曲线Fig.5 The curve of short-circuit reactance of three phase transformer with power factor variation
从图5中可以看出,变压器A、B、C三相短路电抗在线检测值随着功率因数的增加而增大。A相短路电抗最大值为33.729 9Ω,最小值为33.719 1Ω;B相短路电抗最大值为32.834 1Ω,最小值为32.823 6Ω;C相短路电抗最大值为33.731 0Ω,最小值为33.719 1Ω,A、B、C三相的短路电抗最大变化值相对其均值均不超过为0.02%。
综合来看,各相短路电抗值的最大变化幅值均不超过0.02%。采用均值法在线计算其短路电抗值,误差很小。
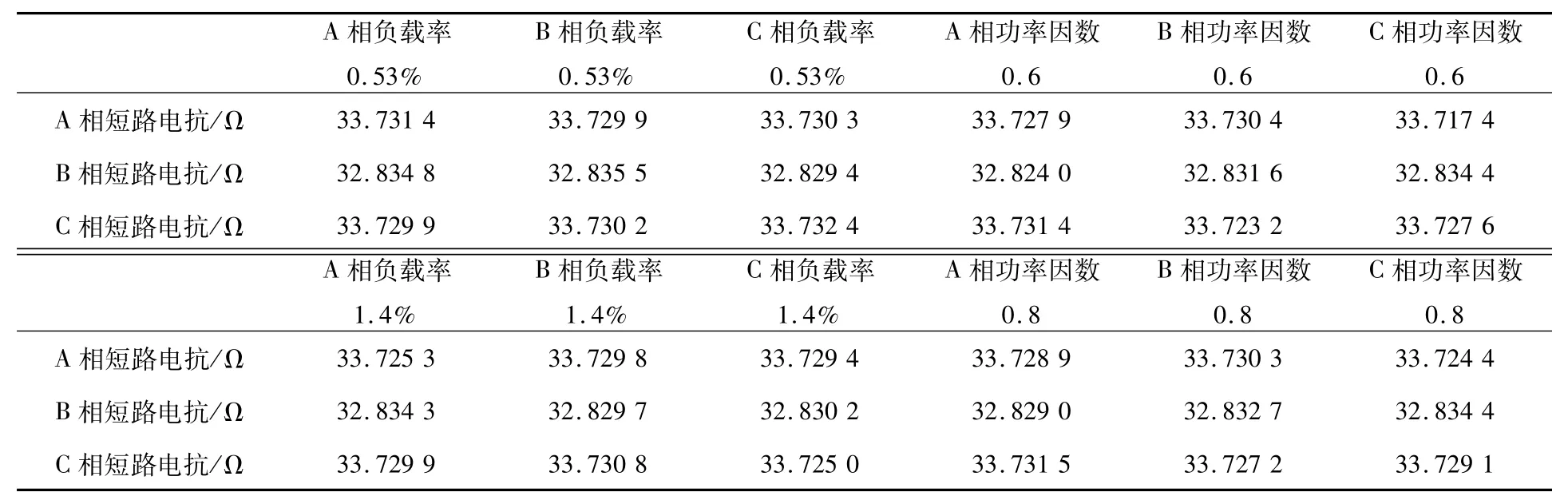
表2 三相不平衡时的A、B、C三相短路电抗值Tab.2 Three-phase short-circuit reactance value of A,B and C under the three-phase unbalanced condition
考虑变压器三相负载极不对称的情况。
(1)A相负载率分别为0.53和1.4,B、C相负载率为额定值;
(2)B相负载率分别为0.53和1.4,A、C相负载率为额定值;
(3)C相负载率分别为0.53和1.4,A、B相负载率为额定值;
(4)A相的功率因数分别为0.6和0.8,B、C相功率因数为1;
(5)B相的功率因数分别为0.6和0.8,A、C相功率因数为1;
(6)C相的功率因数分别为0.6和0.8,A、B相功率因数为1。
其短路电抗计算结果如表2所示。由表中数据可知,变压器出现三相负载极不对称情况时,其三相的短路电抗值与对称时的结果并无明显不同,因此,变压器出现三相不对称时,依然能够利用均值法在线测量变压器短路电抗。
总之,从三相电力变压器的仿真结果可知,所提出的均值法能够用于在线检测变压器绕组变形,其短路电抗值的在线计算误差能够满足测试要求。
4 试验研究
试验研究中,数据采集与处理系统总体结构图如图6所示。将采集到的电压、电流信号传递给后台数据管理中心进行分析计算短路电抗值,并判断绕组是否发生变形[10]。
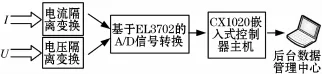
图6 数据采集与处理系统总体结构Fig.6 Overall structure of data acquisition and processing system
对正在运行的三相电力变压器短路阻抗测试,其测试结果的界面如图7所示。

图7 变压器绕组短路阻抗及绕组变形在线检测结果Fig.7 Online detection of short circuit impedance and winding deformation of transformer winding
试验结果表明所提出的方法可以在线检测三相变压器的短路阻抗,并以此为依据在线检测变压器绕组变形。
5 结束语
通过理论分析及仿真试验,验证了所提出的方法可以准确地在线检测三相变压器绕组的短路阻抗;提出的短路阻抗测量方法不受变压器三相负载率、三相负载功率因数、三相负载不平衡的影响。所提出的方法准确、可靠地进行变压器短路阻抗的在线测量,并作为变压器绕组变形的判断依据,为变压器绕组变形在线检测提供了基础。

