AM型随机共振模拟电路的滚动轴承微弱故障检测性能研究
, ,
(石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043)
AM型随机共振模拟电路的滚动轴承微弱故障检测性能研究
柳晓云,马增强,王建东
(石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043)
随机共振理论广泛应用于信号检测中,尤其在滚动轴承微弱故障检测中极其重要。但是对滚动轴承微弱故障检测性能的定量评价问题未做深入研究。在传统随机共振理论的基础上设计了基于调幅(Amplitude Modulation, AM)信号的改进型双稳态随机共振电路,通过Multisim仿真验证了该电路不仅可以实现对大参数故障信号进行故障诊断,还可以有效地削弱直流量的影响,实现滚动轴承微弱故障信号的检测。除此之外,还分析了不同强度噪声对微弱故障检测的影响,以及输入参数变化对电路输出的影响规律,为随机共振电路在滚动轴承微弱故障检测的实际工程应用提供了可靠的科学依据。
随机共振;Multisim;电路设计;微弱信号
0 引言
随着现代科技技术的高速发展,机械设备正朝着大型化、高速化、连续化、集中化和自动化方向发展,设备的组成和结构变得越来越复杂,各系统之间的联系也越来越密切,一旦设备的某个部分在运行过程中出现故障,很可能带来灾难性的后果。应用先进机械状态监测和故障诊断技术不仅可以发现早期故障,避免恶性事故的发生,还可以从根本上解决设备定期维修中的维护不足和过剩维修的问题。然而机械设备早期故障[1-2]中故障信号并不明显,因此微弱信号的检测变得尤为重要。
现有的微弱特征提取方法更多的是从降低噪声、消除噪声的角度出发去检测故障特征[3-5],然而对于淹没在重大噪声中微弱特征信号,如果只是一味的降噪虽然可以降低噪声的干扰能力,但同时也可能会削弱特征信号。Benzie等于1981年提出随机共振[6]理论,此后用于描述非线性系统中内噪声或外噪声的存在可以增加系统的输出响应这一现象,可简单理解为噪声通过非线性系统加强了原本微弱的信号。随机共振理论主要包括绝热近似理论、线性响应理论、驻留时间分布理论、本征值理论。樊养余[7]等提出了随机共振的任意大频率微弱信号检测方法,实现了大频率微弱信号的检测。雷亚国[8]等提出了自适应随机共振的方法并将其应用在故障诊断中,实现了故障特征的提取。何大海[9]等提出了随机共振电路的实现,虽然可以提高故障信号对噪声的比例即信噪比,实现了轴承微弱信号的检测,但是以上方法均没有单独研究参数对轴承故障检测性能的影响,缺少明确的参考依据。
在以上研究的基础上,提出了基于AM的改进型双稳态随机共振电路,实现了大参数信号的故障诊断。并且利用Multisim电路仿真软件分析了不同强度噪声对微弱故障检测的影响,以及输入参数变化对电路输出的影响规律,为随机共振电路在滚动轴承微弱故障检测的实际工程应用奠定了基础。
1 双稳随机共振理论
随机共振系统一般包含3个因素,非线性系统、周期信号以及噪声[10-11]。非线性双稳系统所具有的独特结构特点,为随机共振现象的产生提供了必要的通道机制,而噪声则是产生随机共振现象的前提。当三者达到最佳匹配关系时随机共振对信号的放大作用最明显。最常用的随机共振模型是双稳态系统,由非线性朗之万方程来描述
式中,x(t)为系统输出;s(t)为非线性系统的输入信号;n(t)为随机噪声信号。
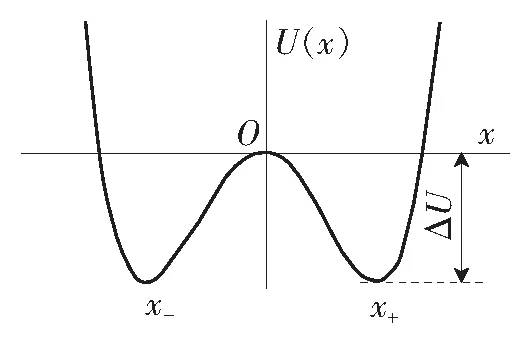
图1 双稳势阱函数示意图
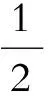
2 调制随机共振系统电路的设计
2.1 调制随机共振系统电路设计方案
基于以上原理,搭建出稳态系统中参数a、b可调的调制随机共振电路,其系统框图如图2所示。
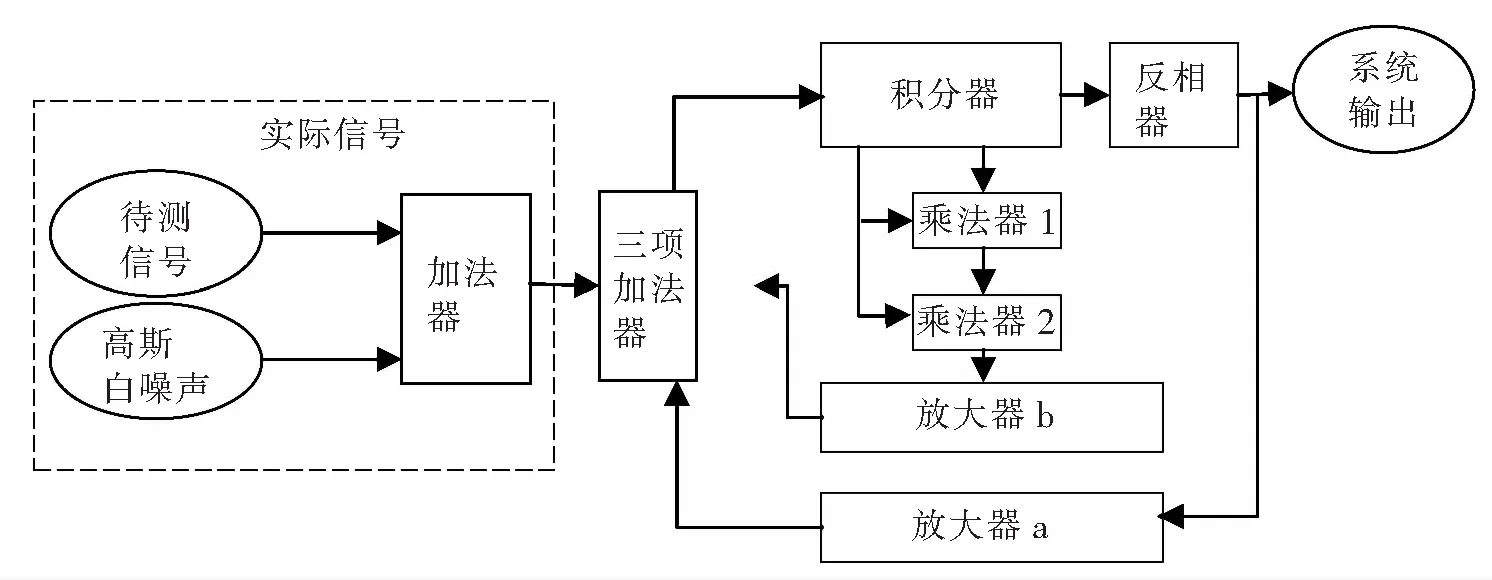
图2 参数可调的调制随机共振电路系统框图
由图2可知,三项加法器接入放大器a、放大器b的反馈,再由积分器、反相器、乘法器和放大器构成非线性双稳态系统。在此系统中,有2个倍数可调的放大器,放大倍数即为a、b。假设积分器的输出为-x,则经过乘法器1后输出为k1x2,再经过乘法器2后输出为-k1k2x3,则放大器b的输出为-bk1k2x3。积分器首先经过反向器,然后经过放大器a后输出为ax,可用数学模型表示为
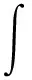
由式(2)可以看出,通过改变a、b的值即可实现参数可调。在实际应用中,首先应调节信号的频率,当其接近待测信号频率时观察系统的输出即可查看输出信号的频率特征,然后再结合微调就可以使输出信号的功率谱峰值更突出,从而判断其产生了随机共振。
2.2 调制随机共振系统电路的实现
由2.1可知,双稳态随机共振系统电路主要由积分器、放大器、反相器、乘法器等构成。各个模块的电路设计如图3~图6。
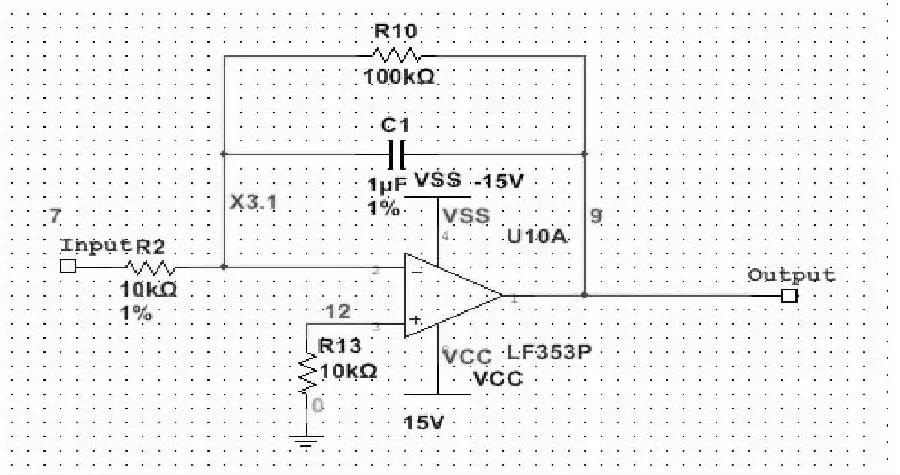
图3 双稳态系统中积分电路
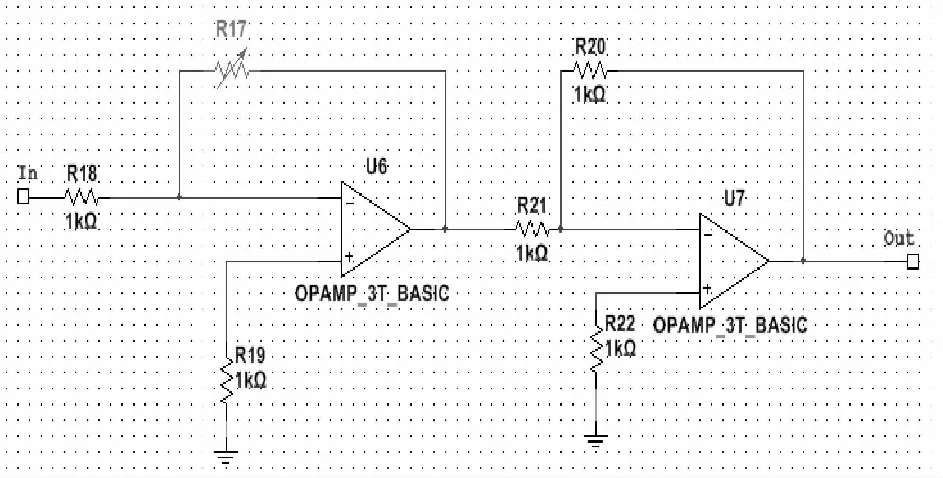
图4 双稳态系统中放大器a、b子电路
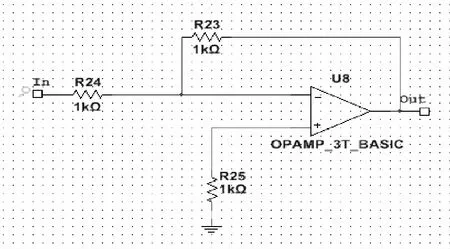
图5 双稳态系统中反相器电路
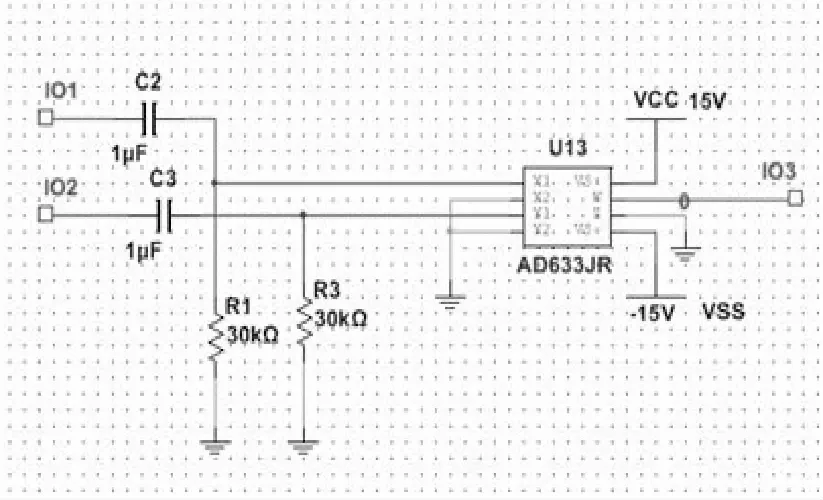
图6 双稳态系统中乘法器电路
相比于传统的方法,为了稳定积分器工作,在电容器两端加了电阻元件。积分电路的原理是基于电容的充放电过程。此积分电路的输入信号来自3个方面,分别是三项加法器的输入信号。因此该电路实现对这3路叠加信号积分。除此之外,传统的随机共振电路在检测故障信号时,输出信号频谱中可能存在直流分量,从而影响随机共振的效果。本文提出电路设计中,为了削弱直流分量,在乘法器的输入端增加了RC高通滤波器,如图6所示。
3 随机共振电路仿真分析
在实际工程应用中,轴承的故障、转速的波动以及轴承的加工误差等诸多原因都会造成轴承振动幅值及转速的波动,从而在振动信号上产生调幅及调频现象,在频谱上表现为在啮合频率及其高阶谐波分量为中心,以调制频率为间隔形成多对调制边带。
设输入信号为

式中,K1为载波信号振幅;K2为调制信号幅值;f1为调制信号频率;f2为载波信号频率。
当输入信号由于固有震荡的影响变为AM型调制信号后,首先应采取平方解调电路进行解调,然后再进入双稳态随机共振电路进行处理。
3.1 平方解调分析原理
将输入信号xm(t)进行平方,可得
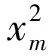
可以看出z(t)中含有的频率分量有f1,f2,2f2,2f2±f1,2f2±2f1,其中直流分量的系数比较大,其他分量相比较小。在解调过程中应先滤除直流,然后再将解调后信号进行随机共振处理,可以观测到f1处有明显峰值,则达到了共振改善信噪比的目的。
3.2 AM型信号的平方解调法电路设计和仿真结果
AM型双稳态随机共振电路如图7所示。令输入调制信号幅值为15 mV,频率为50 Hz,载波信号幅值为1 V,频率为1 kHz。其中V1为噪声源;V2代表为调制信号;V3代表载波信号;XSC1为四踪示波器,用于观察四路通道的输入信号波形;XSA1和XSA2为频谱仪,分别用来分析实际信号和输出信号频谱。
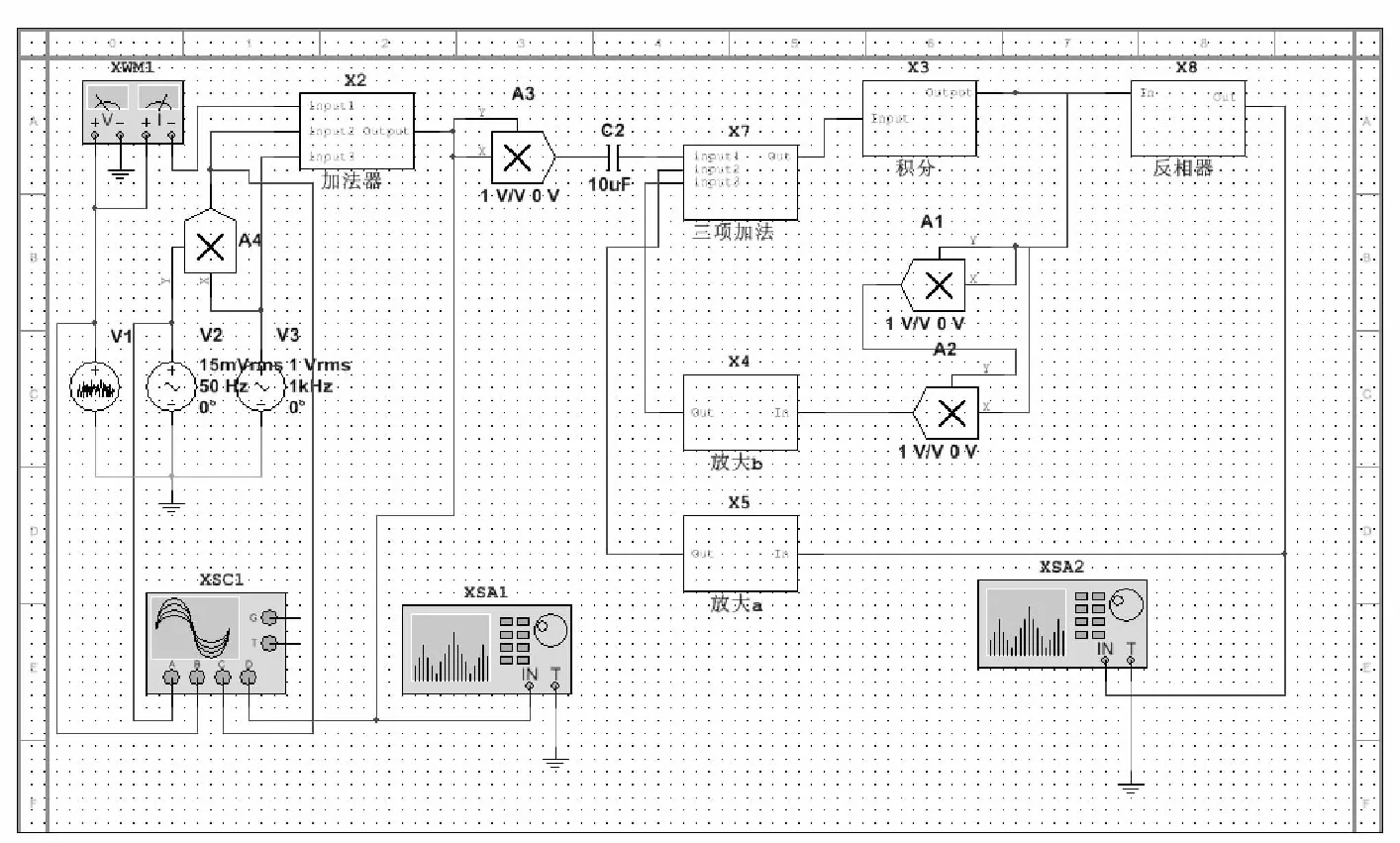
图7 AM型双稳态系统
通过观察XSC1可得到输入信号波形,如图8所示,图中横轴为时间t,纵轴为输出电压幅值。由图中可以看出,四路信号由上到下依次为:调制信号、噪声、DSB信号(调制信号和载波的乘积)和实际信号。然后通过XSA1来观察输入信号的频谱。AM信号频谱如图9所示,图9中横轴为频率f,纵轴为输出电压幅值。从图中可以看到,边带被噪声所湮没,噪声分量分布在整个频段。
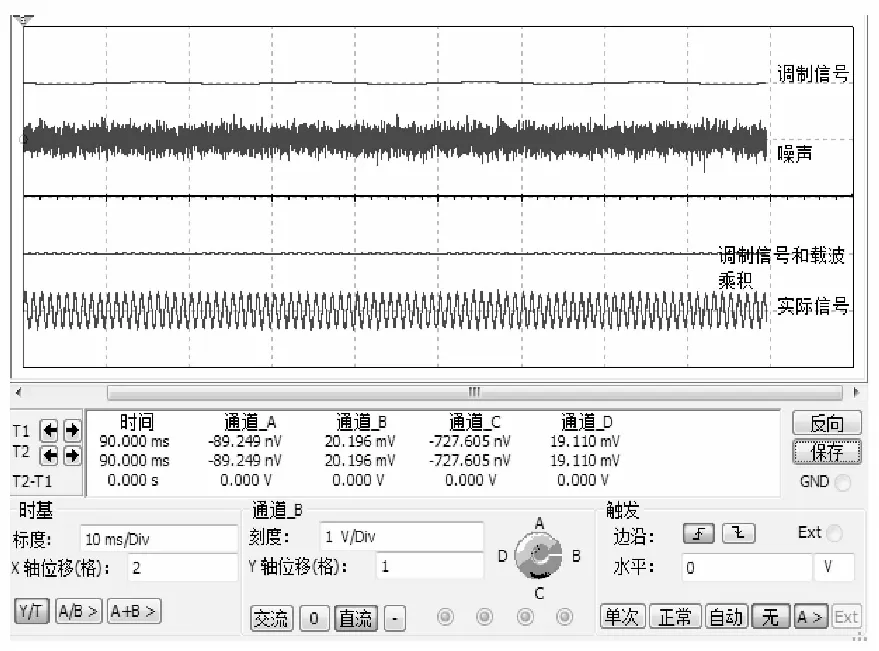
图8 输入信号波形
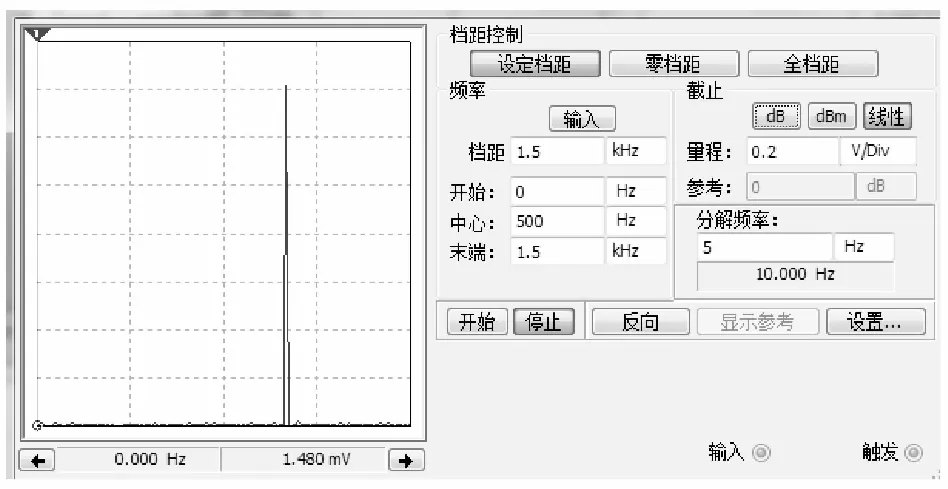
图9 输入信号频谱
通过观察频谱仪XSC2,可看出AM型信号经过平方解调,再经过随机共振系统后的频谱图,如图10。由图10中可以看出,信号经过随机共振系统后,噪声得到了削弱,有用信号频率在一定程度上得到加强,证明了提出方法的有效性。
4 实验结果分析
为了定量地评价滚动轴承微弱故障检测性能,通过改变噪声强度从而改变输入信号信噪比测试出了输入信号信噪比对输出电压幅值的影响曲线,并且讨论了各个输入参数的改变对输出的影响。
4.1 电路的微弱故障检测性能分析
通过改变噪声强度测试出输出电压幅值的影响曲线,如图11所示。
从图11中可以看出,当噪声强度过小时,系统的输出信号不能发生跃迁,即没有发生随机共振现象,输出信号电压幅值较小。随着噪声强度的增大,输出电压幅值不断增大,但是当噪声值超过一定值后,信号检测的效果会逐渐降低。总的来说,在较大噪声范围内,提出方法可有效地提取微弱故障信息,说明了提出方法的有效性。
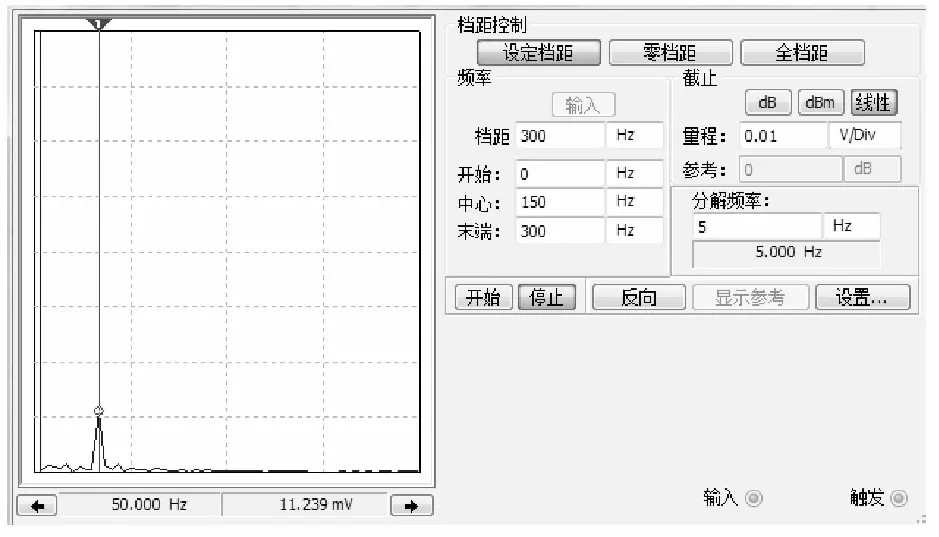
图10 输出信号频谱
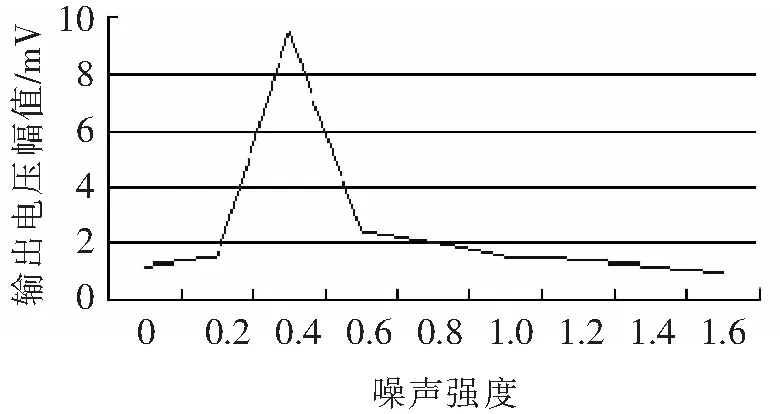
图11 噪声强度-输出电压幅值的影响曲线
4.2 随机共振模拟电路的参数调节规律
该系统中有4个可调参数:K1、K2、f1、f2,下面改变其中一个或多个参数,观察输出的变化。
(1)对参数K1、f1的讨论。
保持K2=1 V,f2=1 kHz不变,令K1=5、10、15、20、25、30、35 mV,分别取f1=50、100、200 Hz,观察输出电压幅值和增益的变化,如图12所示。
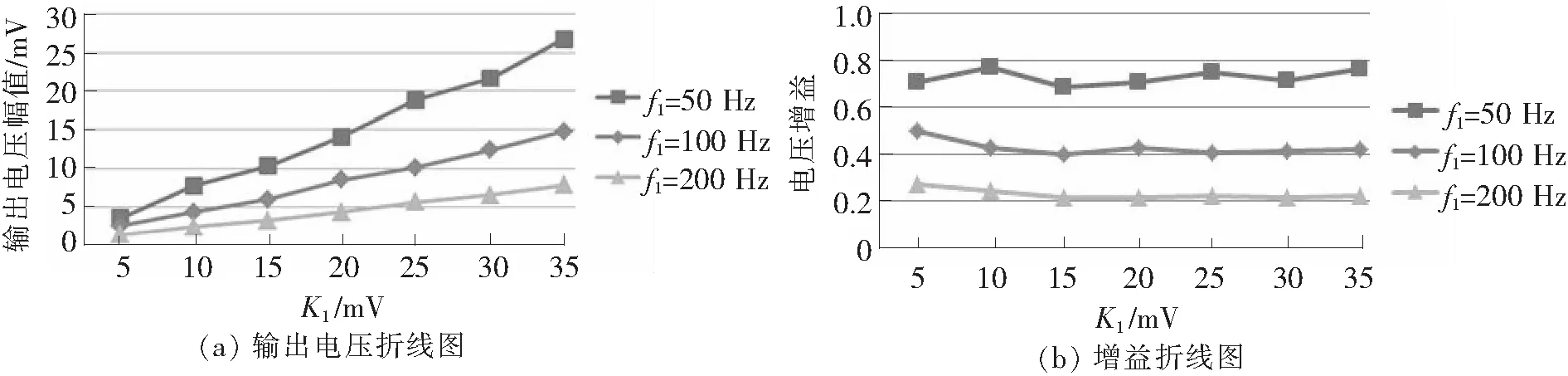
图12 对参数K1、f1的讨论
由图12可以分析得出:
①在频率固定的情况下,输入电压K1和输出电压成线性关系。
②对于不同频率,输出幅值曲线的斜率是固定的,这说明斜率的大小由频率所决定。频率越低,斜率越大,共振输出效果越好。
③从电压增益曲线可以看出,电压增益小于1,表明双稳态随机共振系统对于故障频率起到衰减作用。
④增益曲线基本为横线,这表明增益大小与输入电压基本无关,只与故障信号频率有关。
⑤最大增益小于1,由输出信号频谱可知信噪比得到了改善,这说明故障信号和噪声都得到了衰减,但噪声受到了更多的衰减。
(2)对参数K2的讨论。
K2是调制信号的幅值,同时决定着整个信号的大小,所以推断K2对于输出信号幅值有关。
分别取K1=15 mV,f1=100 Hz,f2=1 kHz,调整K2的取值为0.2~2 V进行实验,得到输出电压曲线和电压增益曲线如图13所示。
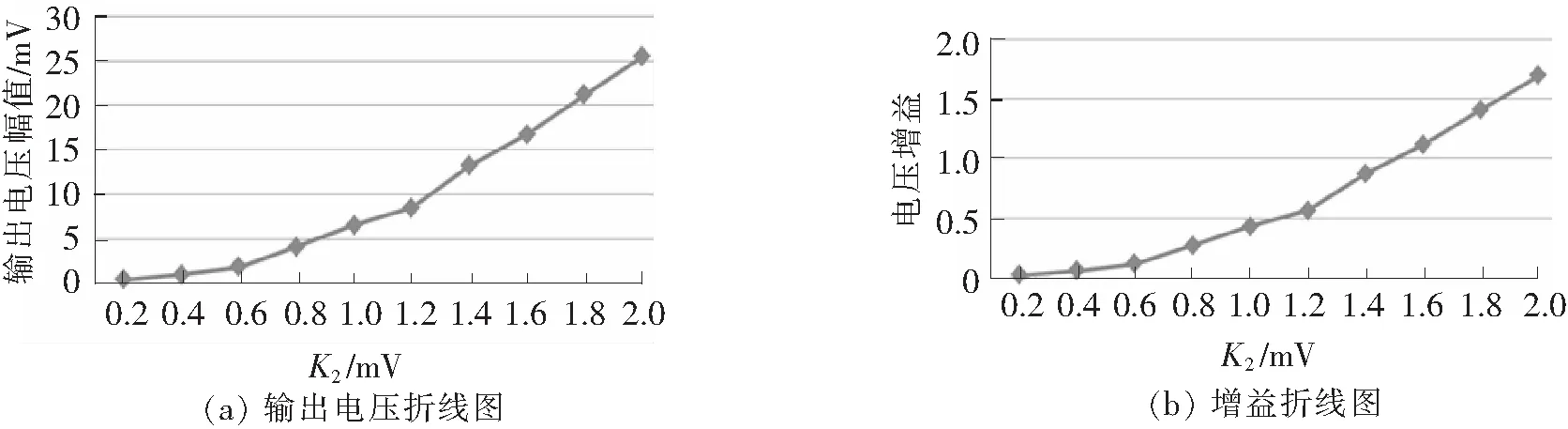
图13 参数K2的讨论
由图13可以得出以下结论:
①输出电压幅值与K2成线性关系,随K2的增大输出电压幅值增大。
②AM型双稳态随机共振系统中,调制信号幅值与电压增益成线性关系,K2越大电压增益越大。电压增益不再是由频率f1。单一决定,而由K2、f1共同决定。
(3)对参数f2的讨论。
分别取K1=15 mV,f1=100 Hz,K2=1 V调整载波信号频率为500~5 000 Hz进行仿真,得到输出电压曲线和电压增益曲线如图14所示。
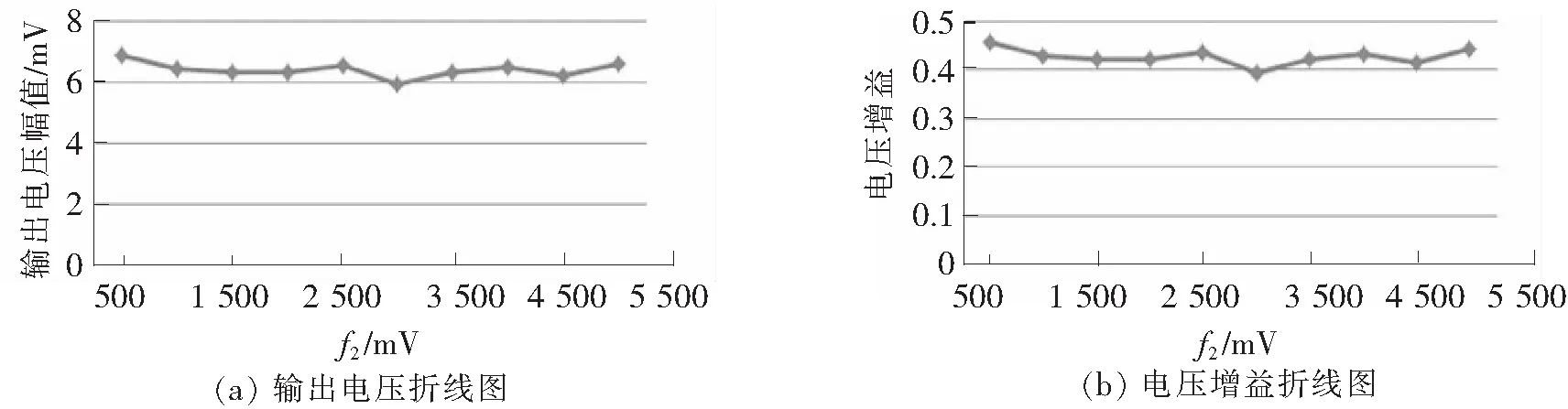
图14 参数f2的讨论
由图14可看出,改变载波频率f2,输出电压幅值和增益近似为一条直线,这表明输出电压幅值和增益与载波频率f2无关,进一步结合f2的物理意义可知,固有震动频率的大小并不会影响到故障的检测。
5 结论
在传统随机共振的基础上,设计了基于AM的改进型随机共振电路。通过仿真实验可以看出,该电路可以实现随机共振,并且可在一定程度上增强故障信号,削弱噪声干扰能力,从而从噪声背景中检测出轴承微弱故障信号。另外,本文还分析了不同强度噪声对滚动轴承微弱故障检测的影响,并且通过改变输入信号的参数,总结出了各个参数的变化对改进型随机共振电路输出的影响规律,为进一步研究随机共振电路在轴承微弱故障信号的检测指明了方向。
[1]李强. 机械设备早期故障预示中的微弱信号检测技术研究[D].天津:天津大学,2008.
[2]杨红娜,郝如江. 基于随机共振的齿轮箱早期故障诊断研究[J]. 石家庄铁道大学学报:自然科学版,2016,29(2):61-66.
[3]王冬云,张文志,张建刚. 小波包能量谱在滚动轴承故障诊断中的应用[J]. 轴承,2010(11):32-36.
[4]段永强. 局部均值分解法在滚动轴承故障自动诊断中的应用研究[D].成都:电子科技大学,2015.
[5]朱文龙,周建中,肖剑,等.独立分量分析-经验模态分解特征提取在水电机组振动信号中的应用[J]. 中国电机工程学报,2013,29:95-101+14.
[6] Reichl L.E.A modern course in statistical physics[D].Austin:University of Texas Press,1980.
[7]樊养余,李利品,党瑞荣. 基于随机共振的任意大频率微弱信号检测方法研究[J]. 仪器仪表学报,2013(3):566-572.
[8]雷亚国,韩冬,林京,等.自适应随机共振新方法及其在故障诊断中的应用[J]. 机械工程学报,2012(7):62-67.
[9]何大海,赵文礼,梅晓俊. 基于随机共振原理的微弱信号检测与应用[J]. 机电工程,2008(4):71-74.
[10] Gammaitoni L.Stochastic Resonance[J].Rev.Mod.Phys,1998,70(1):223-285.
[11] Benzi R,Alfonso S,Vulpiani A.The mechanism of stochastic resonance[J].J.Phys.A,1981,14: 453-457.
ResearchonWeakPeriodicalSignalDetectionPerformanceofRollingBearingBasedonSimulationofAMStochasticResonance
LiuXiaoyun,MaZengqiang,WangJiandong
(School of Electrical and Electronics Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)
The theory of stochastic resonance is widely used in the detection of weak signal, especially in rolling bearing fault detection. However, the quantitative evaluation of the performance of the weak fault detection has not been reported. In this paper, AM stochastic resonance circuit is designed, which is based on the traditional theory of stochastic resonance and the experiments were carried out. The simulation results show that the proposed method can not only reduce the influence of straight flow but also implement the extraction of fault feature. In addition, the performance of the fault detection in the condition of different signal to noise is analyzed, and the influence of input parameters is studied. The research provides a scientific basis for the practical engineering application of the stochastic resonance circuit in the early fault detection of bearing.
stochastic resonance;Multisim;circuit design;weak signal
TH165.3
A
2095-0373(2017)04-0040-07
2016-08-25责任编辑车轩玉
10.13319/j.cnki.sjztddxxbzrb.2017.04.08
国家自然科学基金 (11227201,11372199,11572206);河北省自然科学基金 (A2014210142)
柳晓云(1991-) ,女,硕士研究生,主要从事电气工程的研究。E-mail: 18733104725@163.com
柳晓云,马增强,王建东.AM型随机共振模拟电路的滚动轴承微弱故障检测性能研究[J].石家庄铁道大学学报:自然科学版,2017,30(4):40-45.

