基于区间模糊数的换乘耐受性研究

艾 毅 李宗平

(西南交通大学交通运输与物流学院, 成都 610031)(西南交通大学综合运输四川省重点实验室, 成都 610031)

基于区间模糊数的换乘耐受性研究

艾 毅 李宗平

(西南交通大学交通运输与物流学院, 成都 610031)(西南交通大学综合运输四川省重点实验室, 成都 610031)

从耐受感知的角度,分别针对步行过程和等待过程中的空间要素、时间要素和环境要素进行分析,并提出了空间耐受性、等待耐受性和基于这两者相互叠加而形成的综合耐受性的概念.同时,通过耐受阈值的确定,界定了换乘过程中的耐受极限与实际采取的换乘决策的关系.在进行建模分析时,通过引入区间模糊数,实现了对耐受感知的模糊化处理,提高了参数的回归精度.对模型进行回归分析,得出了不同耐受性的参数估计,并绘制了耐受阈值关于要素叠加的等值面图.研究表明,在常规环境下,人们所能接受的步行距离阈值为381 m,步行等待时间阈值为7.1 min,候车等待时间阈值为12.9 min.同时,该模型可得到换乘者在换乘过程中不同时空要素以及环境要素叠加所引发的耐受感知的变化.

换乘耐受性;耐受感知;耐受阈值;区间模糊数;模糊回归

随着我国现代化、城镇化、机动化进程的快速推进,机动车保有量不断增长,大城市交通拥堵、空气污染等问题也日益突出,这给城市交通系统带来了巨大压力,严重影响了我国城市经济的持续健康发展.因而,优化城市交通结构,引导城市居民绿色出行,已显得非常必要和紧迫.在绿色出行理念下,居民出行结构也发生巨大的变化,“步行+公共交通”的出行换乘组合越来越符合人们的出行要求[1].

在“步行+公共交通”模式中,出行者对换乘过程中各种要素的耐受性很大程度上决定着出行者的决策行为.随着步行交通基础设施的不断完善和改进,良好步行和等待环境所带来的换乘舒适性和耐受性也随之提高.居民不仅可以享受步行换乘所带来的配套服务,例如饮食、多媒体、日常消费等，还可以通过步行换乘减少日常交通支出,提髙健康水平[2].

在大多数换乘耐受性相关研究中,其换乘耐受性主要体现在换乘距离、等待时间2个不同的层面.研究者将这些要素综合考虑到整个换乘成本中,并作为一种惩罚机制,通过研究换乘行为来分析换乘者的耐受性[2-5].但事实上,换乘体验不仅仅涉及这些实际的要素,出行者对外界环境的感知也会对换乘耐受性产生一定影响[5-7].这些由路径复杂性、步行道设施、场站服务设施所引起的心理感受也在一定程度上影响着出行者对换乘距离和换乘等待时间的感知.换乘模式逐渐从公交与公交之间的短距离换乘向公交与轨道交通之间的长距离与多样化换乘模式转换,人们对步行换乘的耐受性也随之发生着改变.本文将重点研究不同环境下换乘者对步行距离、等待时间的耐受性.

1 耐受感知与阈值

随着城市轨道交通网的不断发展,常规公交与轨道交通换乘比例大幅上升.换乘过程面临着从公交与公交之间的短距离、“无缝衔接”式换乘向空间型、多样化的换乘模式转变.这不仅是换乘距离和时间的增加,同时也是换乘体验的变化.本文将以轨道交通和公交之间的换乘空间作为研究对象,并对步行过程和等待过程的耐受性及其环境感知因素进行探讨与量化分析.

1.1 耐受感知要素分析

换乘可以理解为对于时间、体力和心理的一种综合忍受过程,这种过程会受到换乘距离、等待时间和相应的环境体验要素的影响.这种叠加并不是简单的加权,而是心理和生理的叠加.当换乘过程的要素叠加超出一定范围,出行者将无法负担这种换乘消耗而采取其他的换乘策略,这就是换乘的耐受性问题.换乘者通过对换乘要素的叠加变化进行感知,进而判断自身的换乘耐受性.这种基于耐受感知的换乘耐受性分为2个层次:第1个层次是空间耐受性与等待耐受性,空间耐受性是换乘者在步行过程中对步行距离及其环境感知要素的承受能力,等待耐受性是换乘者在等待过程中对等待时间以及环境感知要素的承受能力;第2个层次是综合耐受性,即换乘者对空间以及等待时间的综合承受能力.

在换乘过程中,空间走行距离和等待时间通常作为换乘体验最主要的评价依据,直接影响着出行者的换乘决策[6].空间走行距离可以理解为换乘者从一种交通工具到另一种交通工具的实际走行距离,这种走行距离包括上下扶梯的空间走行.等待时间可以分为步行等待时间与候车等待时间两部分.步行等待时间主要是由人行横道的交通信号等待消耗构成,也包含在途的一些其他随机等待消耗,比如购买物品、寻找路径等.候车等待时间则主要是由排队购票、排队进站和等待车辆时间构成.

人们在实际换乘过程中,有许多要素会影响出行者对步行过程和等待过程的体验.这些感知要素包括路径复杂性、步行道设施、场站服务设施几个方面[7-8].

路径复杂性是出行者在换乘过程中所经历的路径信息,这些路径信息既包含了通过人行横道、过街天桥、地下道路等过街和穿越设施的数量和频率,也与换乘者的具体步行轨迹相关联.Hess[8]认为,步行者不愿在迂回曲折或不连续的人行道上绕来绕去,过于曲折的道路会加重步行者的心理和生理负担,本文将使用步行非直线系数(PRD)——步行网络中两节点间实际道路长度与两点间空间直线距离的比率来量化步行轨迹.同时,过街和穿越设施的数量信息也将是路径复杂性需要研究的另一个方面.

步行道水平是指步行道设备设施和各种辅助配套设施的建设情况,包括步行道比例、绿化及遮蔽比例、生活配套设施和路面整洁情况.步行道主要指道路中用路缘石或护栏及其他类似设施加以分隔的专供行人通行的部分.绿化及遮蔽设施包括行道树、建筑挑檐等[9].沿路配套设施包括超市、餐饮等.

场站服务设施主要指公共交通工具的停靠点以及场站的设备设施建设情况.其设施主要包括遮挡及建筑物、电梯等通行设施、信息提示以及休息候车设施.良好的场站设施和空间布局可以提高乘客的换乘效率和换乘体验,从而提高乘客对候车等待过程的耐受性[10].

随着步行性测量与评价的实证研究展开,直观的步行性网络评价系统随之发展起来.现行指标评价体系主要是行为感知评价方法,其数据来源都需要对大量的受访者进行数据收集.而基于 GIS 街景和场站图像的评价方法则是通过对GPS轨迹信息进行还原所得到的步行道和场站设施的实景还原并进行环境感知要素的分项指标评价,两者可以形成非常好的补充.参考WalkScore建立评价权重体系[11],并对相应指标进行测试和科学优化,得出换乘感知要素及其分项指标的评价体系如表1所示.

表1 环境感知要素及其分项指标评价体系设计

1.2 耐受感知变量与阈值

实际换乘过程中,换乘者很难直观地判断对各项换乘要素的耐受性.因此,需要设置一个过渡变量进行研究.本文通过定义一个耐受感知变量来衡量换乘者感知到的换乘体验与耐受极限的接近程度.耐受感知值越高,说明换乘体验越差.同理,当耐受感知值对于某个要素的变化敏感程度越高(正相关程度越高),那么说明对该要素的耐受性也就越低(见图1).

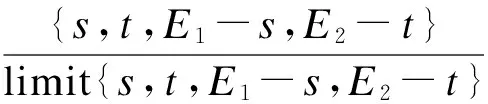
(1)

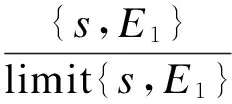
同时,在现实生活中,大多数换乘者一般不会采用换乘消耗非常高的换乘组合作为常用的换乘策略,这就产生了实际换乘阈值的问题.换乘阈值涉及2个层面:空间耐受阈值、等待耐受阈值(见图1).在数据预处理中,本文发现换乘者大多数交通换乘行为的空间耐受感知值和等待耐受感知值一般都位于低于极限值(β=1,δ=1)的某个区间范围内.在交通行为理论研究中,大多数交通行为阈值都设置在其行为样本总量的70%～80%之间[12-16].本文定义空间耐受阈值βc和等待耐受阈值δc为相应耐受感知值的累积分布的0.75处(即相应样本值累积分布的75%处):

βc⟸P(β≤βc)=0.75,δc⟸P(δ≤δc)=0.75

(2)

2 数据挖掘与分析

2.1 数据挖掘

本文采取2种数据挖掘方式相结合的形式对用户的步行、等待过程的耐受性相关数据进行收集与处理:① 基于用户APP;② 基于GIS街景和场站图像还原.

将选取不同性别、不同年龄层的出行者进行调查.每位出行者需下载基于GPS运动轨迹的APP并注册个人账户，填写相关个人信息.在每次换乘开始前打开APP记录换乘轨迹信息并在换乘结束后按照表1所设计的标准填写耐受感知值和环境评价并领取本次的出行补助(见图2).

同时,为了得到步行过程的路径复杂性,本文通过步行轨迹对步行道和场站设施进行GIS图像还原,得到相应的过街和穿越设施的数量、频率和轨迹非直系数.并按照同样的标准对步行道水平和场站设施要素的分项指标进行评分,将由此得到的要素分项指标值与用户提交的要素总评值进行协同分析.数据分类与来源如表2所示.

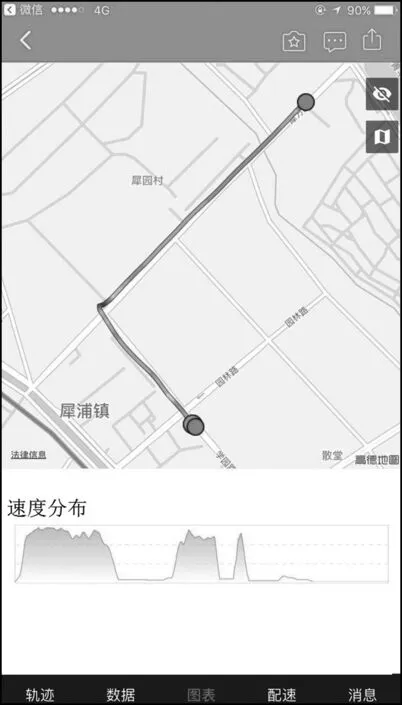
(a) 换乘轨迹与速度分布(b) 步行过程信息(c) 换乘过程评价 (d) GIS图像还原

表2 数据变量列表

通过APP提供的Web数据库来存储所有帐户中的数据,以便进行数据挖掘和分析.其数据挖掘分析框架如图3所示.

为得到换乘耐受性相关数据,本文选取成都市公共交通网作为调查取样空间,并设定数据收集的极限距离为800 m.成都市共开行公交线路428条,地铁线路4条.在统计数据中,步行距离、等待时间等指标均可以得到相对准确的数值,而对于耐受感知值而言,为了降低感知误差,换乘者只需给出一个范围值即可,比如某次换乘的空间耐受感知值为70%～80%.

2.2 换乘行为分析

在成都市进行的交通换乘感知和耐受性实验中,共统计有效样本807份.

图3 换乘数据挖掘与处理框架

图4为不同方式的换乘距离分布,路径复杂性评分和步行道评分均为正向评分,评分越高,容易接受程度越高,即认为越好.由图可见,在步行阶段,随着换乘的模式组合不同,换乘行为也会出现一定的差异.公交到地铁的换乘主要是短距离换乘,其峰值区间集中在50～200 m,平均换乘距离为161 m；而地铁到公交的换乘距离分布相对比较均匀,平均换乘距离为178 m.此外,外界环境也会对换乘者的步行耐受感知产生一定的影响.图5为换乘者对步行过程的评价分布.由图可见,路径复杂性评价位于41～80分区段的情况居多,而步行道的评价相对集中在61～80分的水平上.这种现象反映出换乘者对步行道的满意程度要普遍高于对路径复杂性的满意程度.同时,从图5还可看出,在0～60分区段,路径复杂性对耐受感知的影响相对较大,而在61～80分区段,步行道对耐受感知的影响则更为显著.

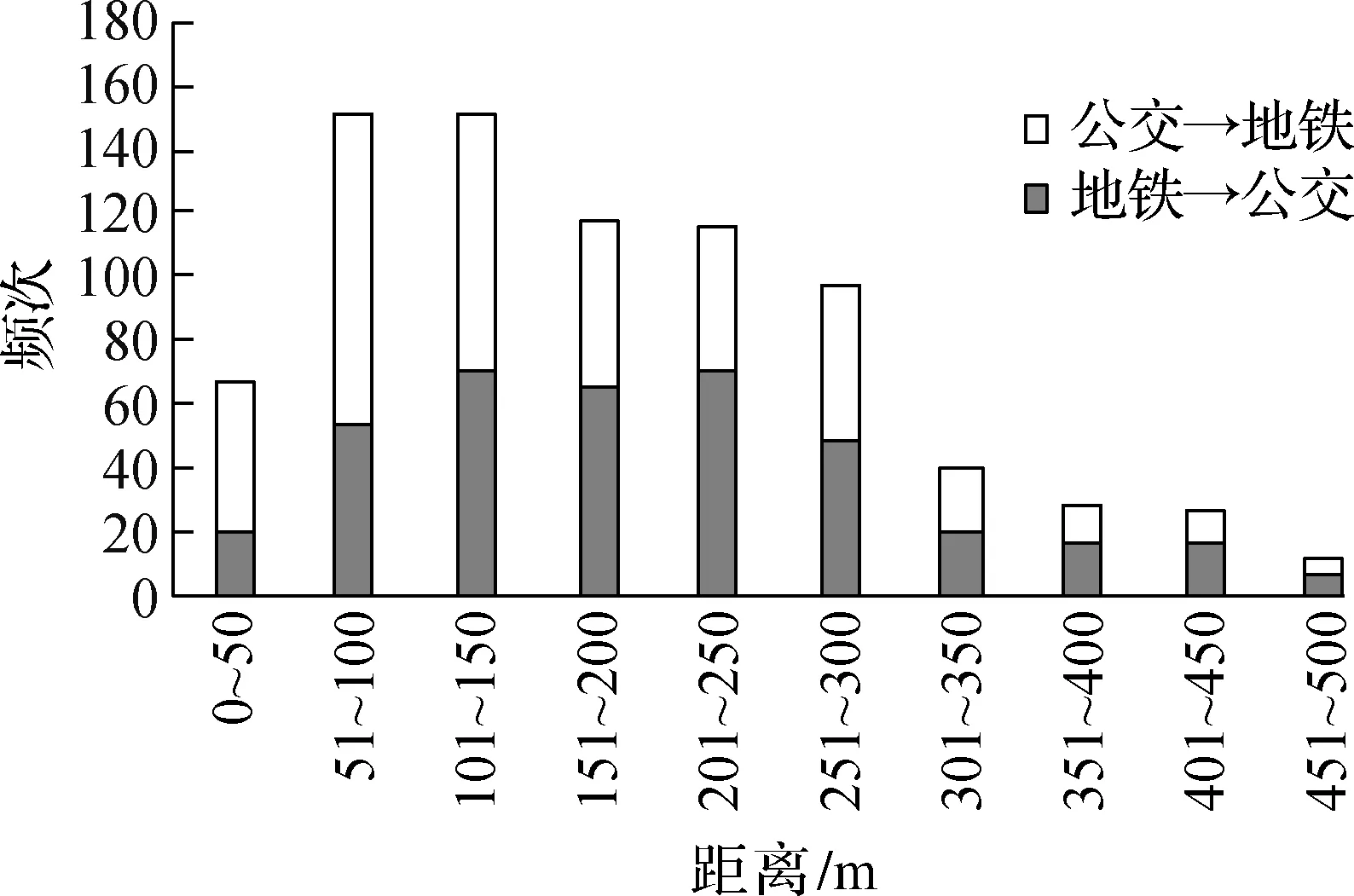
图4 步行距离分布

图5 步行过程评价

通过GIS对街景及场站设施进行路径图像分析并对路径复杂性和步行道分项指标进行评分,结果如图6和图7所示.由图6可以发现在路径复杂性评价中,当过街及穿越设施数量和路径非直线系数在较低水平时,路径复杂性评价与这两者之间的敏感程度也相对较低,且在这个阶段过街及穿越设施数量为主要影响因素.随着这2项的值不断增加,路径复杂性评分下降速率明显变快,这时路径非直线系数变为主要影响因素.从图7可看出,沿路生活配套设施和道路整洁程度评分与步行道评分的一致性较弱,而步行道比例、绿化及遮蔽比例则与步行道评价呈现出较强的一致性.由此可以得出步行道评价受步行道比例、绿化及遮蔽比例的影响程度大于受沿路生活配套设施和道路整洁程度的影响.

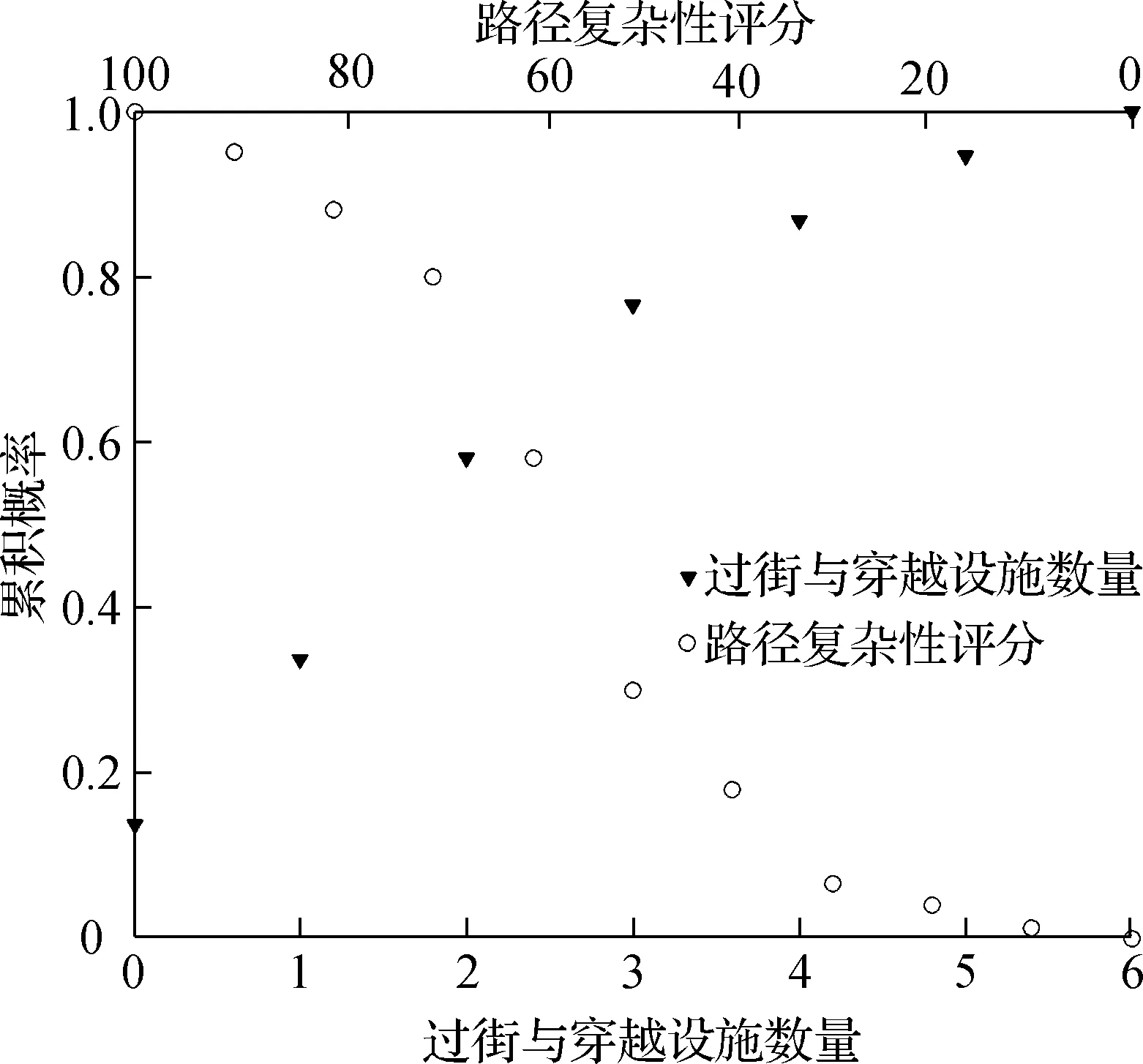
(a) 过街及穿越设施数量和路径复杂性评分

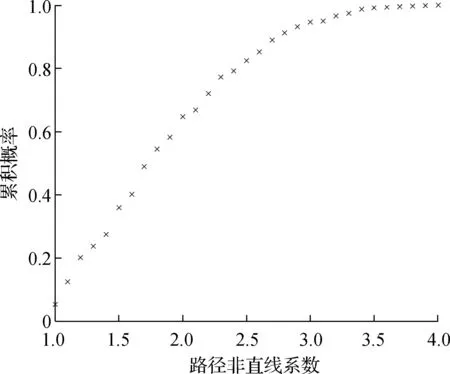
(b) 路径非直线系数

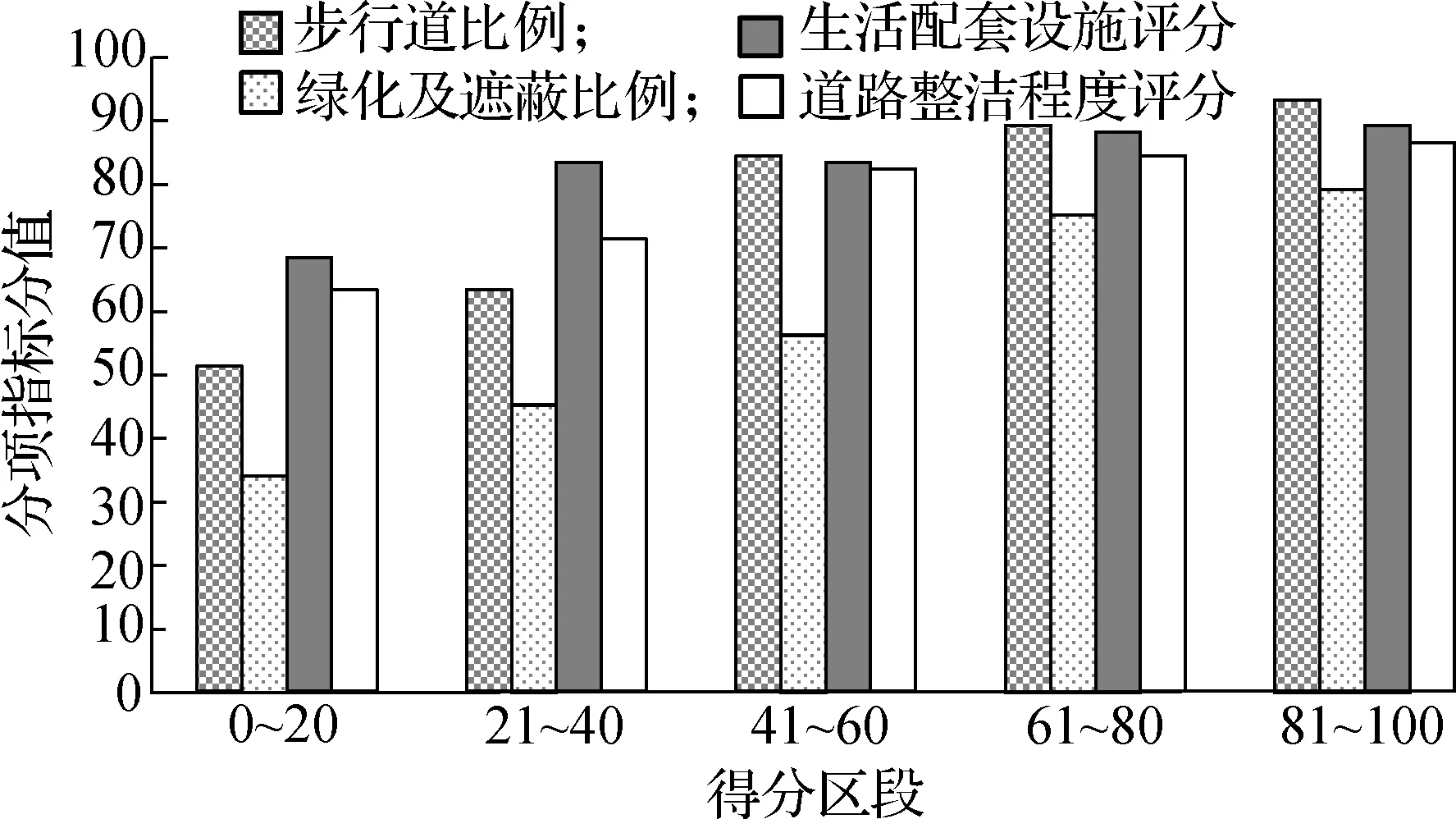
图7 步行道分项指标值分布

步行等待时间主要由人行横道的交通信号等待时间构成,其中也会出现其他行为所产生的时间消耗.当通过的人行横道数量不同时,步行等待时间的分布比例也会发生较大变化.从图8可看出,步行过程中的等待时间分布大多集中在0～4 min的区间内,平均步行等待时间为2.7 min.通过的人行横道数量为0或1时,步行等待时间大多在3 min以内,当通过的人行横道数量高于2次时,步行等待时间通常会大于4 min.相较于步行等待时间,候车等待时间则随交通方式的不同而呈现不同的分布(见图9).对于地铁候车而言,其等待时间大多集中在0～5 min区间,平均等待时间为3.1 min；对于公交候车而言,其时间分布较为均匀,平均等待时间为6.3 min.可看出,公交候车等待时间明显长于地铁等待时间.

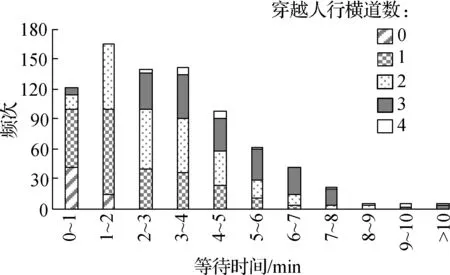
图8 步行等待时间分布

图9 候车等待时间分布

在候车等待阶段,等待环境也会对换乘者的耐受性感知产生一定的影响.图10和图11中场站设施评分及分项指标值均为正向评分,评分越高,容易接受程度越高,即认为越好.从图10可发现,地铁站点的候车环境评价普遍高于公交站点.同时,利用GIS对场站设施进行还原可以得到场站设施分项指标值在换乘者不同评分区间的分布情况,结果见图11,其中纵轴表示这些设施在场站设施评价的不同分值区段出现的比例.从图11中可发现信息提示设施与场站设施评分的一致程度最高,遮挡建筑物和休息候车设施次之.这符合候车的实际心理感受,人们对车辆到达时间的预知需求会很大程度影响对候车时间的耐受性.

图10 场站设施评价分布

图11 场站设施分项指标值分布

3 基于区间模糊数的耐受性模型

通过上述数据分析,可以发现耐受感知是关于空间和时间以及相应的环境感知要素的双层递归的曲线,本文拟建立一种双层模糊回归模型分析递归关系.第1层模糊线性关系包括2部分:① 空间耐受性,即路径复杂性、步行道水平、步行距离与空间耐受感知之间的函数关系;② 等待耐受性,即步行等待时间、候车等待时间、场站设施水平与等待耐受感知之间的函数关系.第2层是综合耐受性,即综合耐受感知关于空间要素和等待要素的模糊线性关系.

3.1 区间模糊数相关定义

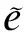
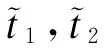
3.2 模糊线性回归模型

自变量X中的元素为实数时[17]

(3)

自变量X中的元素为区间模糊数时

(4)

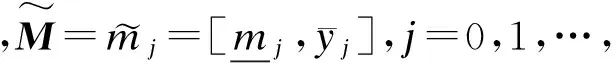
(5)

(6)

同理,当自变量X中元素为实数(即式(3))时,式(6)改写为

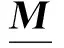
(7)

第1层

步行过程

(8)

等待过程

(9)

第2层

(10)

4 结果分析

4.1 耐受阈值分析

对所收集的耐受感知数据进行累积概率分析,得到空间耐受阈值和等待耐受阈值,如图12所示.耐受阈值很好地界定了耐受极限与一般换乘行为的界限.由式(2)可得,一般换乘者的空间耐受阈值为耐受极限的59%,等待耐受阈值为耐受极限的72%.

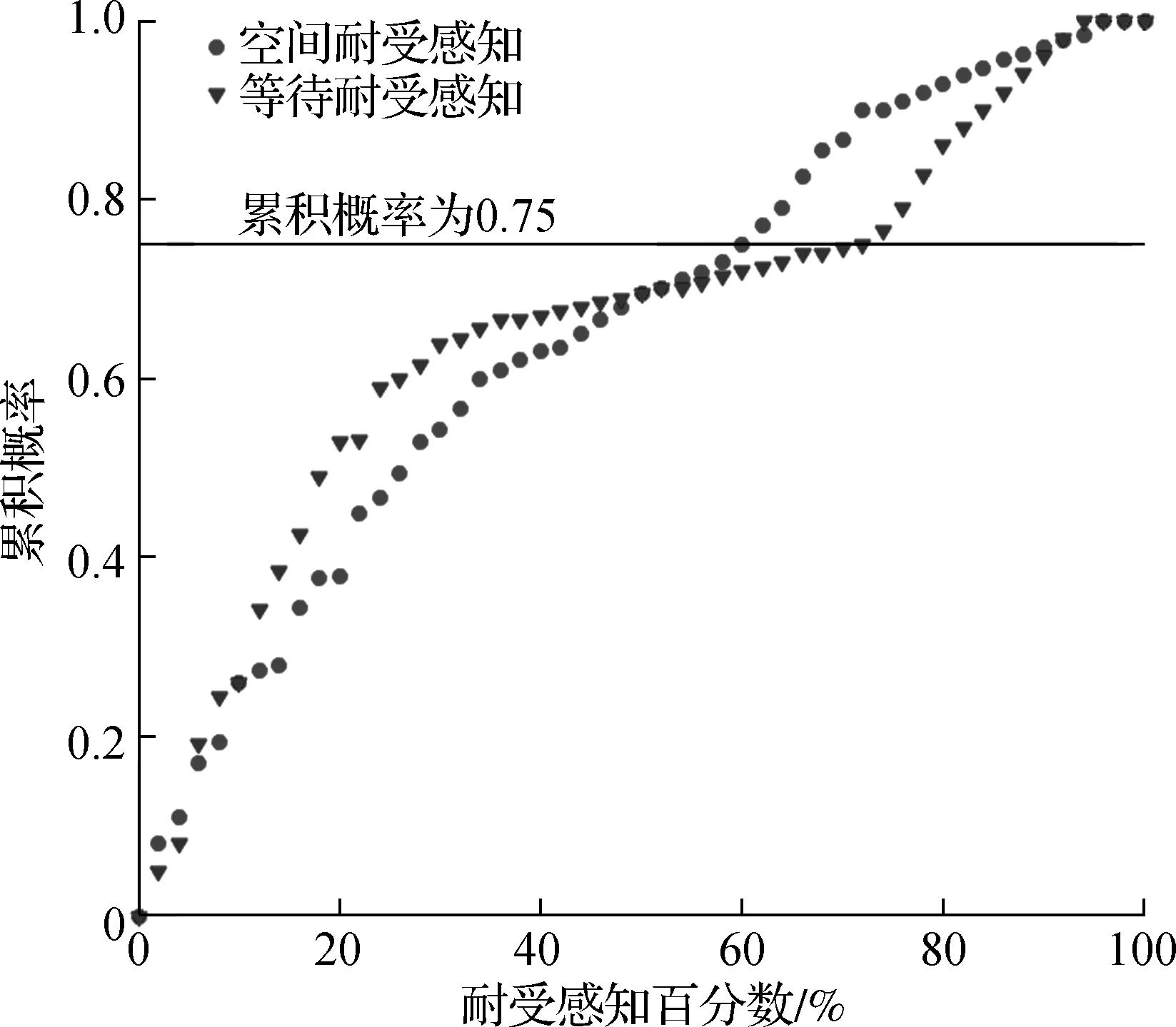
图12 耐受阈值(βc=0.59,δc=0.72)

4.2 模糊回归分析

对数据进行标准化处理,将路径复杂性、步行道评价、场站设施评价转化为标准变量(取值范围为[0,1]),同时将步行距离、步行等待时间、候车等待时间分别除以样本极限值转化为标准变量(步行等待时间极限值为10 min,候车等待时间极限值为15 min).对第1层模型(式(8))的相应参数进行模糊回归,可以分别得到换乘者的空间耐受感知和等待耐受感知的权重分布和回归分析,结果如表3所示.

表3 步行过程与等待过程的模糊回归系数

将空间耐受阈值和等待耐受阈值βc=0.59,δc=0.72代入第1层模糊回归方程式(8),可以得到相应各个变量在阈值条件下的取值变化情况,即相应要素在耐受感知等于阈值时的叠加变化情况(见图13和图14).从图13(a)可看出,实测点在空间耐受阈值的等值面上下界分布均匀,拟合情况较好.步行距离s的阈值上下界分别为350和475 m.当人们的步行距离小于这个区间时,本次步行距离属于较容易被接受的范围.而路径复杂性e1和步行道水平e2的上下界均与相应的X轴和Y无交点,两者均无法在步行距离相对较短时使空间耐受感知达到阈值点，其具体变化情况如图13(b)和(c)所示.同理,从图14(a)可看出,不同等待要素叠加组成的阈值等值面的上下界之间的拟合情况也十分理想.人们可以接受的总等待时间(步行等待时间t1和候车等待时间t2之和)通常小于11～17 min,其具体要素的叠加情况如图14(b)和(c)所示.

(a) 空间耐受阈值的拟合情况 (b) 阈值面下界 (c) 阈值面上界

(a) 等待耐受阈值的拟合情况 (b) 阈值面下界 (c) 阈值面上界

将空间耐受感知和等待耐受感知代入第2层模糊回归模型即式(9)进行参数回归,结果如表4所示.

表4 综合耐受感知参数

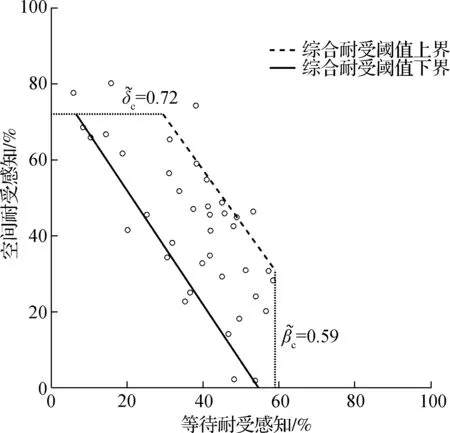
图15 综合耐受性的阈值等值线

图16 常规环境下步行距离、步行等待时间和候车等待时间的组合阈值

5 结论

1) 在实际生活中,人们对耐受性和耐受阈值无法进行直观精确的判断,本文通过基于区间模糊数的线性回归模型的建立,对耐受感知进行模糊化处理,大大提高了参数估计精度.

2) 通过回归分析发现,在空间耐受性中,换乘者对步行距离的耐受性最弱,对路径复杂性和步行道水平的耐受能力相对较强.而在等待耐受性中,换乘者对步行等待时间和候车等待时间的耐受性相对较弱,对场站设施水平的耐受能力较强.

3) 本文通过模型绘制出步行过程和等待过程的阈值上下界的等值面图,更直观地反映出这种阈值条件下不同换乘要素之间的耐受性叠加比较.同时,本文得出的结论与国外相关研究的结论在等待时间分布上基本一致,但步行距离普遍偏大,这与我国许多城市以及成都的地铁线网还不发达存在必然联系[1-3,10-13].

)

[1] Randall T A, Baetz B W. Evaluating pedestrian connectivity for suburban sustainability[J].JournalofUrbanPlanningandDevelopment, 2001,127(1): 1-15. DOI:10.1061/(asce)0733-9488(2001)127:1(1).

[2] Park S, Choi K, Lee J S. To walk or not to walk: Testing the effect of path walkability on transit users’ access mode choices to the station [J].InternationalJournalofSustainableTransportation, 2015,9(8): 529-541. DOI:10.1080/15568318.2013.825036.

[3] Jensen W A, Brown B B, Smith K R, et al. Active transportation on a complete street: Perceived and audited walkability correlates [J].InternationalJournalofEnvironmentalResearchandPublicHealth, 2017,14(9): E1014. DOI:10.3390/ijerph14091014.

[4] 周乐, 戴继锋. 城市交通规划体系框架下的步行和自行车交通[J]. 城市交通, 2014, 12(4): 19-26. DOI:10.13813/j.cn11-5141/u.2014.0404.

Zhou Le, Dai Jifeng. Pedestrian and bicycle transportation in urban transportation planning system[J].UrbanTransportofChina, 2014,12(4): 19-26. DOI:10.13813/j.cn11-5141/u.2014.0404.(in Chinese)

[5] 张林, 焦伟赟, 曹力. 综合客运枢纽步行换乘模型研究[J].交通标准化, 2014, 42(23): 18-21.

Zhang Lin, Jiao Weiyun, Cao Li. Pedestrian transfer model of integrated passenger hub[J].TransportationStandardization, 2014,42(23): 18-21. (in Chinese)

[6] Hoogendoorn-Lanser S. Modelling transfers in multi-modal trips: Explaining correlations[J].TransportationResearchRecord:JournaloftheTransportationResearchBoard, 2006,1985(1):144-153.

[7] 王若成. 基于换乘人耐受限的对向公交换乘生存距离模型研究[J]. 中国安全科学学报, 2015, 25(2):123-127. DOI:10.16265/j.cnki.issn1003-3033.2015.02.021.

Wang Ruocheng. Research on survival model for bus transfer based on endurance limit of passengers[J].ChinaSafetyScienceJournal, 2015,25(2): 123-127. DOI:10.16265/j.cnki.issn1003-3033.2015.02.021.(in Chinese)

[8] Hess P M. Measures of connectivity [Streets: Old paradigm, new investment] [J].Places, 1997,11(2): 58-65.

[9] Vargo J, Stone B, Glanz K. Google walkability: A new tool for local planning and public health research? [J].JournalofPhysicalActivityandHealth, 2012,9(5): 689-697. DOI:10.1123/jpah.9.5.689.

[10] Jun H J, Hur M. The relationship between walkability and neighborhood social environment: The importance of physical and perceived walkability[J].AppliedGeography, 2015,62: 115-124. DOI:10.1016/j.apgeog.2015.04.014.

[11] Hirsch J A, Moore K A, Evenson K R, et al. Walk score®and transit score®and walking in the multi-ethnic study of atherosclerosis[J].AmericanJournalofPreventiveMedicine, 2013,45(2): 158-166. DOI:10.1016/j.amepre.2013.03.018.

[12] Li Y, Wang Z X. Measuring visual enclosure for street walkability: Using machine learning algorithms and Google Street View imagery [J].AppliedGeography, 2016,76: 147-153. DOI:10.1016/j.apgeog.2016.09.024.

[13] Guo Z, Wilson N H M. Assessing the cost of transfer inconvenience in public transport systems: A case study of the London Underground[J].TransportationResearchPartA:PolicyandPractice, 2011,45(2): 91-104. DOI:10.1016/j.tra.2010.11.002.

[14] Daniels R, Mulley C. Explaining walking distance to public transport: The dominance of public transport supply[J].JournalofTransportandLandUse, 2013,6(2): 5-20. DOI:10.5198/jtlu.v6i2.308.

[15] El-Geneidy A, Grimsrud M, Wasfi R, et al. New evidence on walking distances to transit stops: Identifying redundancies and gaps using variable service areas[J].Transportation, 2013,41(1): 193-210. DOI:10.1007/s11116-013-9508-z.

[16] Alshalalfah B W, Shalaby A S. Case study: Relationship of walk access distance to transit with service, travel, and personal characteristics[J].JournalofUrbanPlanning&Development, 2007,133(2): 114-118. DOI:10.1061/(asce)0733-9488(2007)133:2(114).

[17] Hojati M, Bector C R, Smimou K. A simple method for computation of fuzzy linear regression[J].EuropeanJournalofOperationalResearch, 2005,166(1): 172-184. DOI:10.1016/j.ejor.2004.01.039.

Analysisoftransfertolerancelimitbasedonintervalfuzzynumber

Ai Yi Li Zongping

(School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China) (Comprehensive Transportation Key Laboratory of Sichuan Province, Southwest Jiaotong University, Chengdu 610031, China)

From the view of tolerance perception, the spatio-temporal factors in the walking and waiting process are analyzed, and the concepts of space tolerance, waiting tolerance and the comprehensive tolerance based on the superposition of the former two are proposed. Meanwhile, through the determination of the tolerance threshold, the limit of the tolerance in the transfer process and the actual transfer decision are determined. During the analysis of the model, the fuzzy processing of tolerance perception is realized by introducing the interval fuzzy number, which greatly improves the accuracy of the results. Finally, through the regression analysis of the bi-level recursive fuzzy model, the parameter estimation of different processes is obtained, and the contour map of the tolerance threshold value with regard to the superposition of factors is drawn. The results show that the walking distance threshold is 381 m, the waiting time threshold is 7.1 min and the threshold of the time for waiting a vehicle is 12.9 min in the conventional environment. Furthermore, the model can be used to obtain the changes of the perceived tolerance caused by the changes of the time and space factors and the environmental factors in the transfer process.

transfer tolerance; tolerance limit; transfer threshold; interval fuzzy number; fuzzy regression

10.3969/j.issn.1001-0505.2017.06.027

U491

A

1001-0505(2017)06-1253-10

2017-03-08.

艾毅(1988—)，男，博士生；李宗平(联系人)，男，博士，教授，博士生导师，zpli@swjtu.cn.

国家自然科学基金资助项目(51578465).

艾毅，李宗平.基于区间模糊数的换乘耐受性研究[J].东南大学学报(自然科学版),2017,47(6):1253-1262.

10.3969/j.issn.1001-0505.2017.06.027.