蚁群算法在自适应索穹顶结构内力控制中的应用
陆金钰 鲁 梦
(1东南大学混凝土及预应力混凝土教育部重点实验室, 南京 210096)(2东南大学土木工程学院, 南京 210096)
蚁群算法在自适应索穹顶结构内力控制中的应用
陆金钰1,2鲁 梦2
(1东南大学混凝土及预应力混凝土教育部重点实验室, 南京 210096)(2东南大学土木工程学院, 南京 210096)
为调控索穹顶结构形状、提高刚度、减少内力,在索穹顶结构中装入了能够改变构件长度的作动器.以结点位移、容许应力、作动杆作动范围为约束条件建立内力优化模型,目标是使结构工作状态系数f最小.利用蚁群随机搜索算法求出该优化模型的最优解.最后以一平面索穹顶结构为算例进行计算,验证了本算法的可行性及控制效果.此算例根据作动器安装位置的不同,分11种工况分别讨论控制效果.结果表明,蚁群随机搜索算法易于收敛,可以得出较好解;各工况的内力均不同程度地实现了优化,其中在内圈斜索设作动器的工况下,内力的优化效果最好;索穹顶结构通过杆件长度的调整,可达到形状调整、受力最优的目的.
自适应索穹顶; 内力控制; 蚁群算法; 主动控制
索穹顶由预应力提供刚度,是一种缺陷敏感结构,且结构预应力与其几何形状相互耦合.在传统索穹顶结构上安装传感器、作动器及控制器可构造一种智能索穹顶结构,该结构通过传感器对环境实时检测,利用控制器将检测结果反馈给作动器,通过作动器变形以改变杆件长度,从而达到调整结构形状及内力的目的,这就是“以不变应万变”的思想[1],类似于文献[2]提到的无限刚度思想.据此,沈黎元等[3]采用力法方法提出预应力索结构的线性位移控制方法.肖南等[4-5]以结构工作状态系数最小为目标构造线性规划模型,研究了张力结构的形状控制问题.李莎等[6-7]研究了自适应索杆张力结构的形态问题,以索穹顶为算例进行验证.程华强等[8]研究了自适应张弦梁在移动荷载和风荷载作用下的控制.Noack等[9]通过在张弦梁中安装液压作动器研究了在移动荷载作用下单撑杆张弦梁结构控制理论;Sobek等[10]研究了在移动荷载下双撑杆张弦梁结构的控制理论;隋允康等[11-12]利用线性规划方法研究了智能桁架结构最优控制方法,并进行了数值模拟.聂润兔等[13]以最短行程和最小导出内力为目标,利用模拟退火法实现了自适应桁架结构在线弹性范围内的结构静态形状控制.Zhong[14]提出了基于结构矩阵分析理论的预应力位移控制方法,并验证了该方法准确性;Kmet等[15]开展了索穹顶内力及位移主动控制试验研究.
本文在传统索穹顶中引入作动器,以索穹顶的结构工作状态系数f为优化目标,以作动器的主动变形量为变量,以结构的关键结点位移受限、作动器参数以及保证拉索不松弛为约束条件,构造结构内力优化模型.基于Matlab求解此结构模型,得到作动杆最佳调节量,通过改变杆件长度以调整结构形状,实现构件在荷载下受力最优、结构刚度增加的目的.最后通过算例证明了此方法的正确性和有效性.
1 结构优化模型
为实现自适应索穹顶的主动调控,需要建立结构优化模型.首先定义结构工作状态系数:
(1)
式中,f为结构工作状态系数;kz为各杆件工作状态系数.
构造如下优化问题:求作动器作动量δr(r=1, 2, …,p),使f最小,且满足
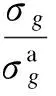
(2)
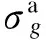
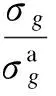
(3)
式(3)可保证拉索受拉,压杆受压.
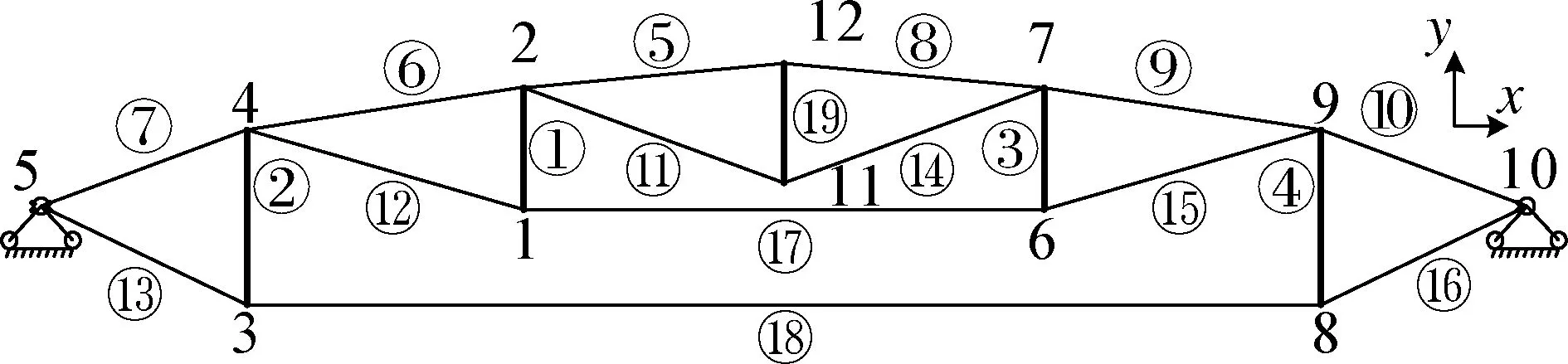
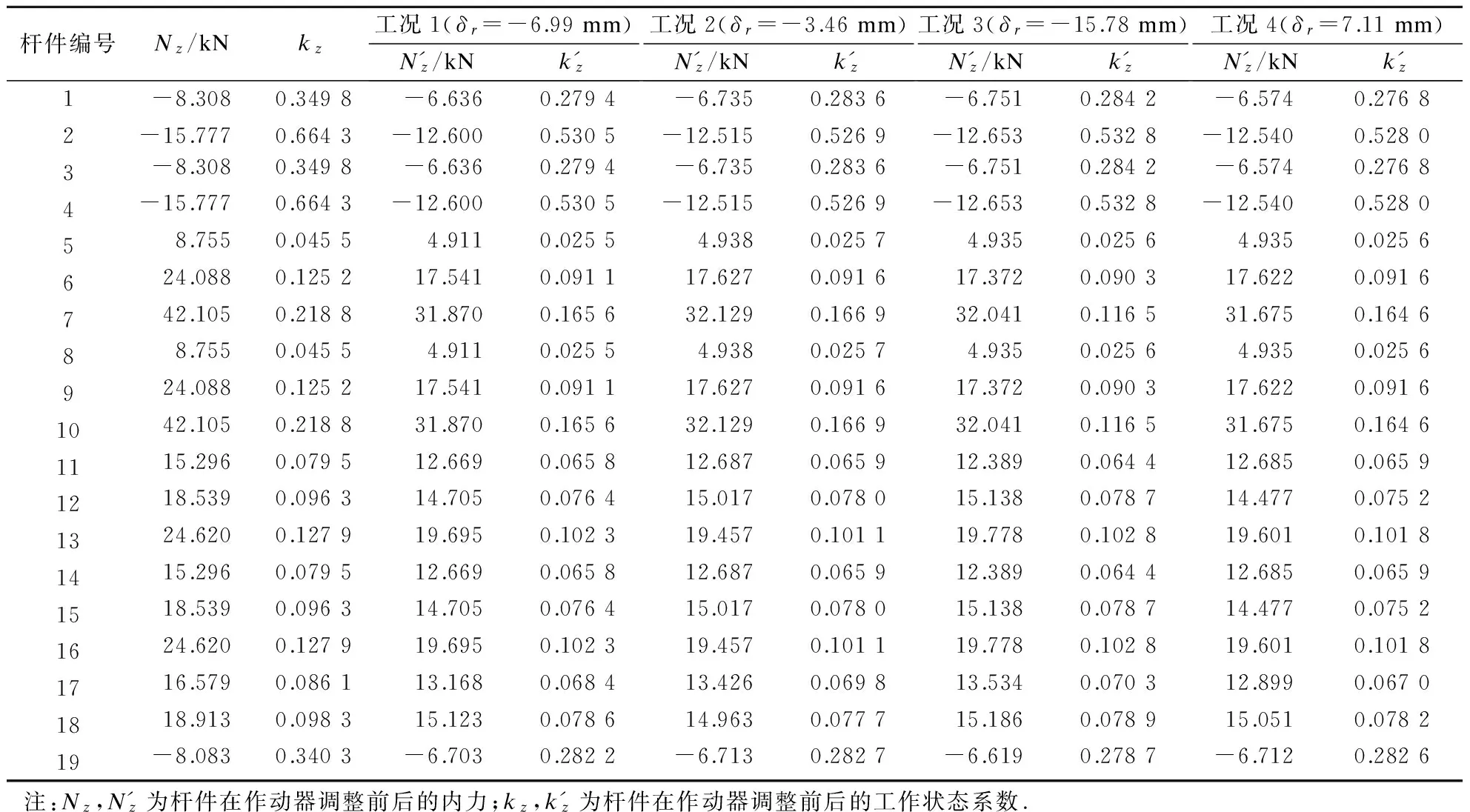
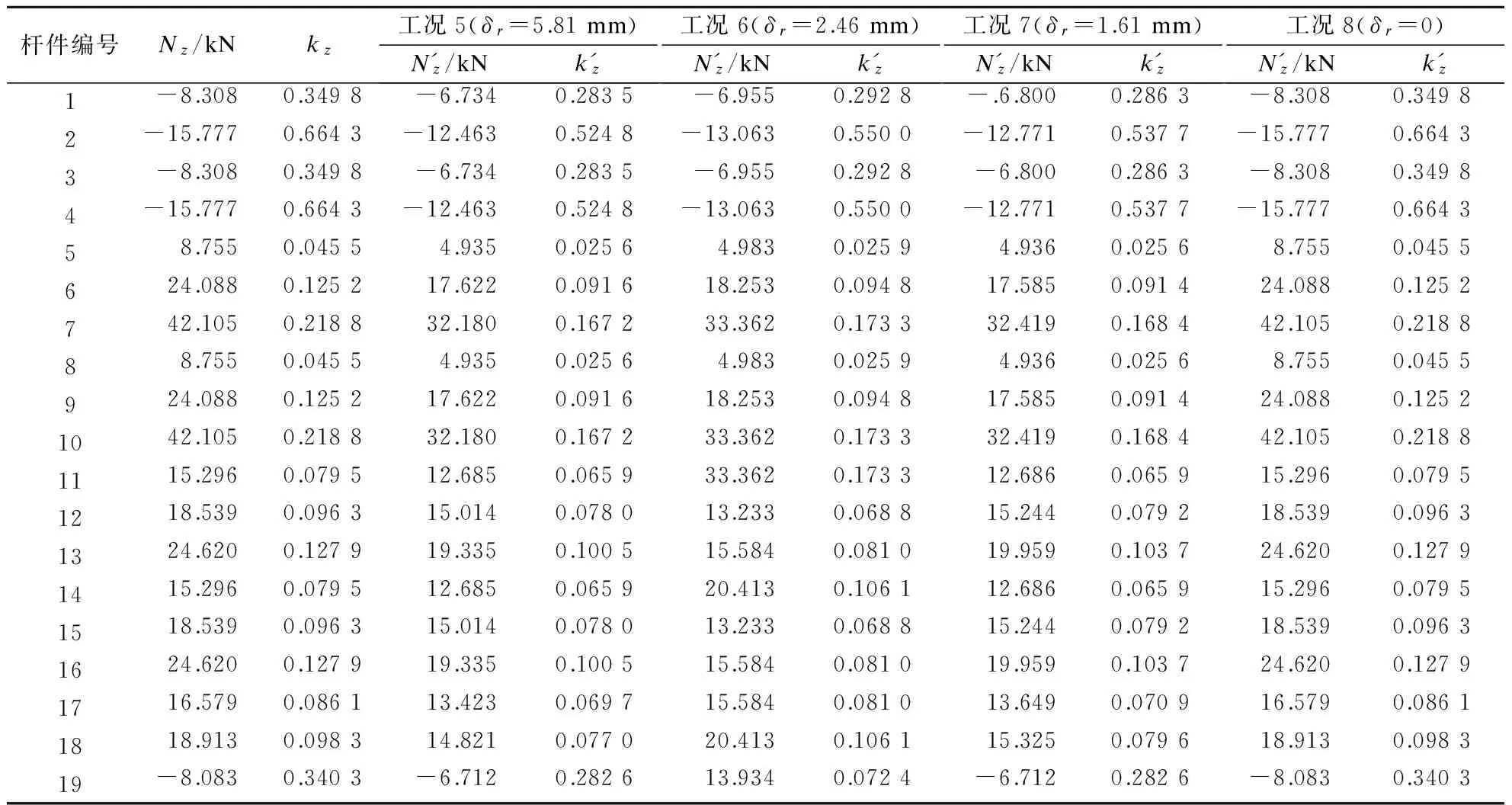
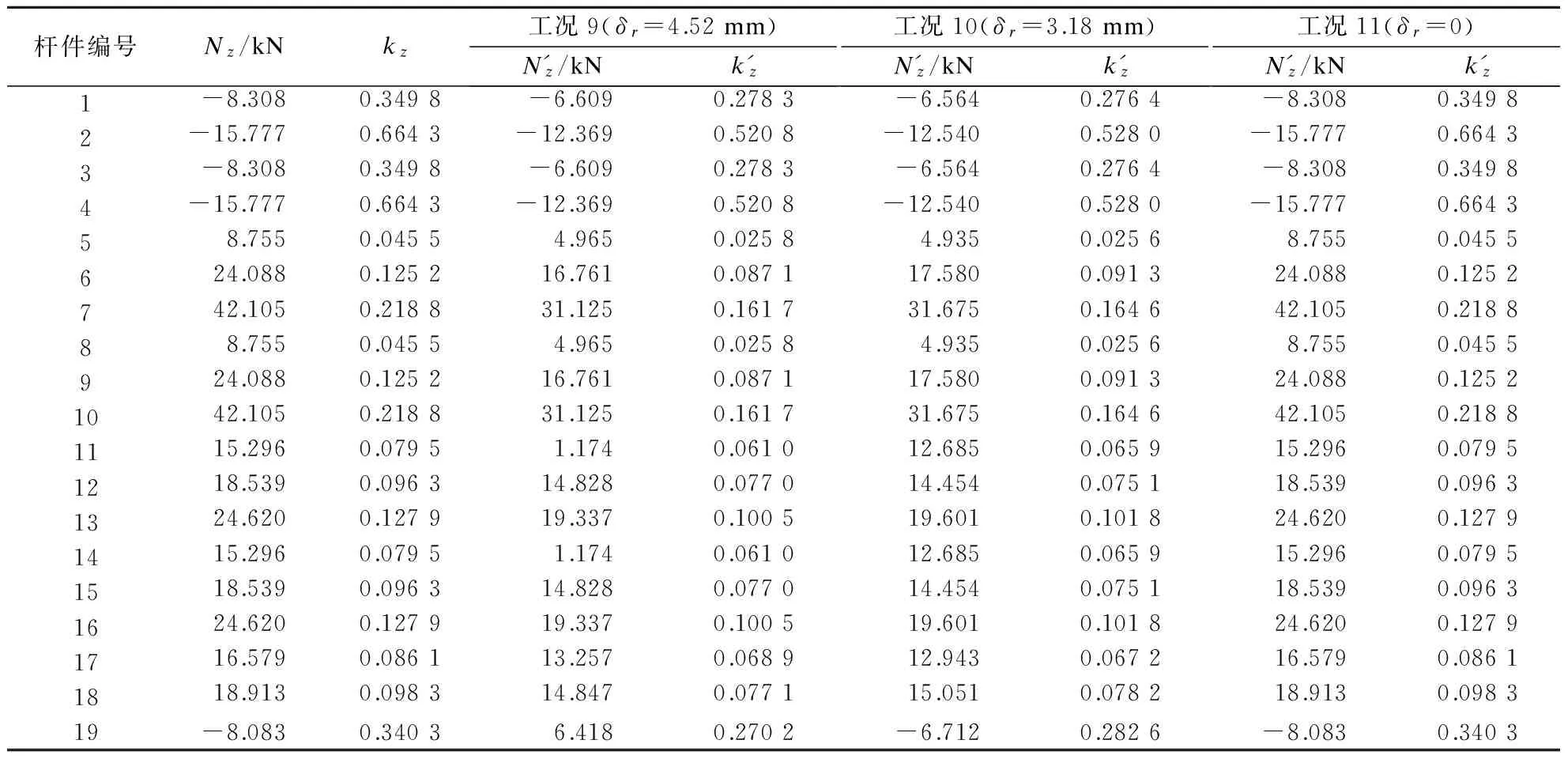
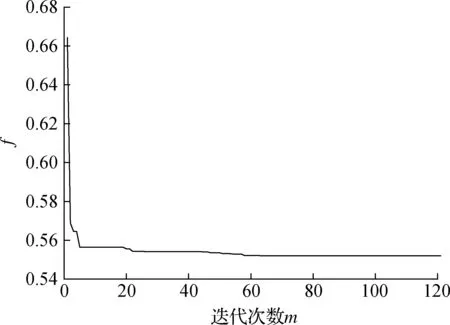
-[u]q (4) 式中,uq为关键结点在自由度q上的位移.式(4)可保证关键结点位移不超过限值. (5) -h≤δr≤h (6) 式中,δr为作动器主动工作产生的变形;±h为伸缩调整量.式(6)为作动杆允许作动范围. 为求各杆件在作动杆作动后实际内力,首先要对结构进行灵敏度分析.灵敏度即主动单元变化单位长度引起的结点位移或单元内力[7]. 单元切线刚度Kij为 (7) (8) 结点位移u对任一主动单元长度变化量的灵敏度为 (9) 杆件内力t的灵敏度为 (10) 式中,en为主动单元n的变化量;KT为整体刚度矩阵;B为由Bij按照几何拓扑组成的整体协调矩阵;T=diag(E1A1/L1,E2A2/L2, …,EvAv/Lv)(v=1, 2, …,w),为线弹性刚度对角矩阵,其中Ev,Av分别为v号单元弹性模量和截面积;δ为作动器伸长量向量,δ中对应x号主动单元位置元素为1,其余元素为0. (11) 式中,ngr为r杆变化单位长度时g杆的内力变化量,即内力灵敏度值;p为作动器数量. 作动器工作后结点在自由度q上的位移可表示为 (12) 式中,uqr为r杆变化单位长度时在自由度q上的位移变化量,即位移灵敏度值. 为准确度量结构工作状态,杆件在外力作用下的工作状态系数可定义为[4] (13) 通过在原有结构杆件中加入控制作动器,可调节结构的形状,改变原有结构的工作状态系数及所对应的结构内力分布,使得结构的工作状态系数最小,此时调整形状以后的状态称为结构的最合理工作状态. 为求解结构优化模型中作动器的最佳作动量,本文采用蚁群随机搜索算法求解上述问题.与其他启发式算法相比,蚁群算法[16]具有很强的鲁棒性和搜索较好解的能力;作为一种基于种群的进化算法,易于并行实现;同时蚁群算法采用正反馈机制.将蚁群算法应用于本文优化问题中,在一定程度上可加快优化过程,利于发现较好解.蚁群搜索算法用蚂蚁行走路径表示待优化问题的可行解,蚂蚁群体的所有路径即构成了待优化问题的解空间.路径较短的蚂蚁释放信息素量较多,然后随着时间的推进,较短路径上累积的信息素浓度也逐渐增大,选择该路径的蚂蚁个数也越来越多.最后蚂蚁群体会在正反馈作用下集中到最佳路径上,此时对应的便是待优化问题最优解. 蚁群算法具体过程如下: ① 初始化参数[16].蚂蚁的数量为20,蚂蚁的移动次数为200,信息素挥发系数为0.9,转移概率常数P0为0.2,并且根据约束条件(5)设置搜索范围即变量上下限制量,最大迭代次数mmax,迭代初值m=1,设置ξ. ② 根据约束条件式(2)~(5)随机设置蚂蚁的初始位置,构建解空间. ③ 每次迭代后,计算所有蚂蚁的状态转移概率,并根据概率大小进行相应的局部搜索和全局搜索,并判断解是否越界.再比较状态转移后求得的目标函数值与状态转移前的目标函数值fm. ⑤ 更新信息素,m=m+1,并返回步骤③. ⑥ 若m 本文根据上述算法,编制了相应的Matlab程序求解此形状调整优化问题. 葵花形索穹顶是一种典型索穹顶结构形式,具有很好的应用前景,故本文选取该结构为数值算例,其平面结构构型如图1所示.设结构跨度为5 m,矢高为1.2 m.压杆为φ20 mm×4 mm的Q235空心钢管,材料弹性模量206 GPa,许用应力210 MPa;索为直径12.7 mm钢绞线,弹性模量185 GPa,不退出工作最小应力50 MPa,许用应力1 950 MPa;作动器容许轴力60 kN,最大调整量100 mm.图1中杆件①~的初始预应力分别为-6.875,-13.750,-6.875,-13.750, 16.770, 28.346, 43.481, 16.770, 28.346, 43.481, 11.402, 15.373, 21.478, 11.402, 15.373, 21.478, 13.750, 16.500,-6.000 kN.设结点12受到竖直向下荷载F=5 kN作用. 图1 平面索穹顶结构构型 要求在杆件中加入作动器,并在作动器工作后,结构的受力状态最合理即结构工作状态系数f最小,其关键结点位移限值为-8 mm≤[ux]≤8 mm,-15 mm≤[uy]≤15 mm.考虑结构的对称性,本文只讨论了对称布置作动器的工况.根据作动器安装位置的不同,分11种工况分别讨论控制效果:工况1为杆件①、③(中圈压杆)设作动器;工况2为杆件②、④(外圈压杆)设作动器;工况3为杆件(内圈压杆)设作动器;工况4为杆件(中圈环索)设作动器;工况5为杆件(外圈环索)设作动器;工况6为杆件⑤、⑧(内圈脊索)设作动器;工况7为杆件⑥、⑨(中圈脊索)设作动器;工况8为杆件⑦、⑩(外圈脊索)设作动器;工况9为杆件、(内圈斜索)设作动器;工况10为杆件、(中圈斜索)设作动器;工况11为杆件、(外圈斜索)设作动器. 各工况下的内力、工作状态系数及作动器的调节量如表1~表3所示,调整前后结构的工作状态系数f如表4所示.由表可看出,在11种作动器布置方案中,控制外圈脊索(工况8)或外圈斜索(工况11),无法使索穹顶结构性能得到改善.除工况8、工况11外,其余9种工况均不同程度实现了内力优化(达20%左右),其中内圈斜索(工况9)的优化效果较好,内圈脊索(工况6)优化效果相对较差.在工况1~7,9,10下,结构工作状态系数分别降低了20.14%,20.68%,19.79%,20.52%,21.00%,17.21%,19.06%,21.60%,20.52%.其中工况9下结构工作状态系数收敛曲线如图2所示. 结构关键结点(上弦结点2,4,7,9,12)的位移如表5所示,可看出结构受力最合理时均能满足位移限值要求,且拉索均未退出工作. 表1 工况1~4下杆件内力及结构工作状态系数 表2 工况5~8下杆件内力及结构工作状态系数 表3 工况9~11下杆件内力及结构工作状态系数 表4 不同工况下结构工作状态系数 算例表明,在作动器工作之前,结构的内力分布并不是最优状态.在结构单元中引入作动器,当作动器工作后,在相同荷载作用下,结构的刚度大大提高,变形可控,满足使用要求,并且通过合理地布设作动器,调整了结构形状,内力实现重分布,可以达到杆件受力最合理的目的. 1) 索穹顶结构通过杆件长度的主动调整,使结构形状改变,实现了结构刚度增加、受力最优的目的. 2) 以结构工作状态系数最小为目标,以作动器主动变形量为未知量,考虑索的应力约束、结点的位移约束以及作动器参数等约束条件,建立了优化模型,基于蚁群算法编制了相应求解程序. 3) 算例表明,在相同荷载作用下,通过作动器调整索穹顶形状后,可使杆件受力最合理.控制外圈脊索(工况8)或外圈斜索(工况11)均没有优化效果;内圈斜索(工况9)优化效果较好,内圈脊索(工况6)优化效果较差. ) [1] 隋允康, 邵建义. 自适应超静定桁架结构强度控制的研究[J]. 固体力学学报, 2001, 22(2): 136-142. DOI:10.3969/j.issn.0254-7805.2001.02.004. Sui Yunkang, Shao Jianyi. Research on strength control for adaptive structure of statically indeterminate truss[J].ActaMechnicaSolidaSinica, 2001,22(2): 136-142. DOI:10.3969/j.issn.0254-7805.2001.02.004. (in Chinese) [2] Senatore G, Winslow P, Duffour P, et al. Infinite stiffness structures via active control[C]//InternationalAssociationforShellandSpatialStructures. Eindhoven, the Netherlands, 2015:1-12. [3] 沈黎元, 李国强, 罗永峰. 预应力索结构位移控制[J]. 同济大学学报(自然科学版), 2006, 34(3): 291-295. DOI:10.3321/j.issn:0253-374X.2006.03.002. Shen Liyuan, Li Guoqiang, Luo Yongfeng. Displacement control of prestressed cable structures[J].JournalofTongjiUniversity(NaturalScience), 2006,34(3): 291-295. DOI:10.3321/j.issn:0253-374X.2006.03.002.(in Chinese) [4] 肖南, 肖新, 董石麟. 张力结构形状调整优化分析[J]. 浙江大学学报(工学版), 2009, 43(8): 1513-1519. Xiao Nan, Xiao Xin, Dong Shilin. Optimization analysis of shape adjustment of tension structure [J].JournalofZhejiangUniversity(EngineeringScience), 2009,43(8): 1513-1519. [5] 肖南, 黄玉香, 董石麟, 等. 张力结构位移限制下的形状调整强度优化分析[J]. 浙江大学学报(工学版), 2010, 44(1): 166-173. Xiao Nan, Huang Yuxiang, Dong Shilin, et al. Strength optimization analysis of tensegrity structure by shape adjustments under restricted displacements [J].JournalofZhejiangUniversity(EngineeringScience), 2010,44(1): 166-173. (in Chinese) [6] 李莎, 肖南, 董石麟. 自适应索杆张力结构内力和形状同步调控研究[J]. 华中科技大学学报(自然科学版), 2014, 42(8): 119-122,127. DOI:10.13245/j.hust.140824. Li Sha, Xiao Nan, Dong Shilin. Research on simultaneous control of force and shape for adaptive cable-strut tensile structures[J].JournalofHuazhongUniversityofScienceandTechnology(NatureScienceEdition), 2014,42(8): 119-122,127. DOI:10.13245/j.hust.140824.(in Chinese) [7] 李莎, 肖南, 董石麟. 变长度单元自适应索杆张力结构响应灵敏度分析[J]. 华中科技大学学报(自然科学版), 2014, 42(10): 119-123. DOI:10.13245/j.hust.141024. Li Sha, Xiao Nan, Dong Shilin. Sensitivity analysis on responses of adaptive cable-strut tensile structure with length changeable elements[J].JournalofHuazhongUniversityofScienceandTechnology(NatureScienceEdition), 2014,42(10): 119-123. DOI:10.13245/j.hust.141024.(in Chinese) [8] 程华强, 罗尧治, 许贤. 自适应张弦梁结构的非线性内力控制[J]. 浙江大学学报(工学版), 2014, 48(7): 1155-1161. Cheng Huaqiang, Luo Yaozhi, Xu Xian. Nonlinear force control of adaptive beam sting structure[J].JournalofZhejiangUniversity(EngineeringScienceEdition), 2014,48(7): 1155-1161.(in Chinese) [9] Noack T, Ruth J, Müller U. Adaptive hybrid structures[C]//InternationalConferenceonAdaptableBuildingStructures. Eindhoven, the Netherlands, 2006: 256-260. [10] Sobek W, Teuffel P. Adaptive systems in architecture and structural engineering[C]//SPIE’s8thAnnualInternationalSymposiumonSmartStructuresandMaterials. Newport Beach, CA, USA, 2001: 36-45. DOI:10.1117/12.434141. [11] 隋允康, 邵建义. 自适应结构多工况下强度控制的研究[J]. 力学学报, 2002, 34(2): 223-228. DOI:10.3321/j.issn:0459-1879.2002.02.010. Sui Yunkang, Shao Jianyi. Research on strength control for adaptive structure under multi-loading cases[J].ActaMechanicaSinica, 2002,34(2): 223-228. DOI:10.3321/j.issn:0459-1879.2002.02.010.(in Chinese) [12] 隋允康, 邵建义. 作动器参数对结构性能的影响和调整受力状态的实施策略模拟[J]. 计算力学学报, 2002, 19(2): 159-165,172. DOI:10.3969/j.issn.1007-4708.2002.02.007. Sui Yunkang, Shao Jianyi. Influence of parameters of actuators and simulating of adjusting force-bearing state[J].ChineseJournalofComputationalMechanics, 2002,19(2): 159-165,172. DOI:10.3969/j.issn.1007-4708.2002.02.007.(in Chinese) [13] 聂润兔,邵成勋,邹振祝. 自适应桁架形状控制中主动杆多目标最优配置[J]. 应用力学学报,1997,14 (3):48-53. Nie Runtu, Shao Chengxun, Zou Zhenzhu. Multi objective optimal allocation of active rod in adaptive truss shape control [J].ChineseJournalofAppliedMechanics, 1997,14(3):48-53.(in Chinese) [14] Zhong Y. Displacement control of prestressed structures[J].ComputerMethodsinAppliedMechanics&Engineering, 1997,144(1):51-59. DOI:10.1016/s0045-7825(96)01164-4. [15] Kmet S, Mojdis M. Adaptive cable dome[J].JournalofStructuralEngineering—ASCE, 2014,141(9): 04014225. DOI:10.1061/(asce)st.1943-541x.0001189. [16] 温正. 精通Matlab智能算法[M]. 北京:清华大学出版社, 2015:284-311. Applicationofantcolonyalgorithmininternalforcecontrolofadaptivecabledome Lu Jinyu1,2Lu Meng2 (1Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China) Actuators which can change members’ length actively are introduced into cable dome for shape adjustment, enhancing the stiffness and reducing the interal forces. An internal force optimization model is established for minimizing the working state coefficient subjected to the restricted nodal displacements, allowable stress and working parameters of the actuator. The optimal solution of the optimization model is obtained by the ant colony search algorithm. The control effects are discussed in 11 different conditions according to the installation position of the actuator. Finally, a planar cable dome is studied as a numerical example to verify the feasibility and effectiveness of the optimization algorithm. The results show that the ant colony search algorithm is easy to converge, and a better solution can be obtained. The internal forces of each working condition are optimized in different degrees, and the internal force optimization effect of the condition that the actuator is installed in the inner diagonal cable is the best; the shape of the cable dome can be adjusted and the force can be optimized through the length adjustment of the member. adaptive cable dome; internal force control; ant colony algorithm; active control 10.3969/j.issn.1001-0505.2017.06.013 TU3 A 1001-0505(2017)06-1161-06 2017-04-18. 陆金钰(1981—),男,博士,副教授, davidjingyu@gmail.com. “十三五”国家重点研发计划资助项目 (2016YFC0800206)、国家自然科学基金资助项目(51778129)、 江苏省自然科学基金资助项目(BK20161422). 陆金钰,鲁梦.蚁群算法在自适应索穹顶结构内力控制中的应用[J].东南大学学报(自然科学版),2017,47(6):1161-1166. 10.3969/j.issn.1001-0505.2017.06.013.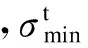
2 作动器工作结构分析
2.1 灵敏度分析
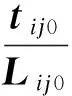
2.2 结构工作状态系数
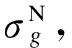
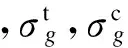
3 蚁群算法
4 算例

5 结论
(2School of Civil Engineering, Southeast University, Nanjing 210096, China)

