一种用于OFDMA认知网络的低复杂度资源分配算法

宋晓勤 刘 叶 金 慧 雷 磊 胡 静 宋铁成

(1南京航空航天大学电子信息工程学院, 南京 211106)(2东南大学信息科学与工程学院, 南京 210096)

一种用于OFDMA认知网络的低复杂度资源分配算法

宋晓勤1刘 叶1金 慧1雷 磊1胡 静2宋铁成2

(1南京航空航天大学电子信息工程学院, 南京 211106)(2东南大学信息科学与工程学院, 南京 210096)

针对功率受限的多用户正交频分多址接入(OFDMA)认知网络,提出了一种低复杂度的资源分配算法,包括子载波和功率分配.在子载波分配中,选取包含最差信道质量的子载波优先分配给用户,再将剩余的子载波信道质量值按方差的降序分配给用户,避免了最后未被分配的子载波恰好只能分配给对应信道质量最差用户的情况发生;在功率分配时,在传统线性注水算法的基础上增加了对主用户抗干扰阈值的判断,在最大化次用户吞吐量的同时,提高了主用户的抗干扰能力.仿真结果表明,与已有算法相比,该算法能够有效提升分配给用户的最差子载波信道质量,在用户吞吐量上接近于传统线性注水算法的性能上限,具有良好的主用户公平性,且计算复杂度低.

OFDMA;子载波分配;功率分配;用户吞吐量

随着无线通信设备和服务不断增加,频谱资源紧缺的问题日益突出.而传统的固定频率分配方式又造成授权频段在某些时间、某些区域的无线频谱资源闲置[1].认知无线电(CR)[2]正是为了解决频谱资源匮乏与利用率低下的矛盾而出现的技术,该技术实现了次用户(SUs)的机会式频谱接入,合理利用主用户(PUs)的频谱空穴[3],使得频谱利用率得到了显著提高.

作为对抗宽带无线通信传输过程中频率选择性衰落的有效手段,正交频分复用(OFDM)技术由于其节省带宽、实现简单的优点被广泛地应用于各种CR网络中[4-5].特别是当其应用于多用户环境而构成正交频分多址接入系统(OFDMA)时, 由于具有更加灵活的资源分配方式以及更高的多用户分集增益,因此应用前景广阔[6-7].

多用户资源分配包括子载波和功率分配.对于一个子载波总数给定的OFDMA系统而言,子载波分配问题的最优解可由基于图论的Hungarian算法求出[8].然而,对于时变无线信道而言,Hungarian算法复杂度非常高.因此,有必要设计一种低误码率、低复杂度的分配算法.文献[9]提出了普通贪婪算法,以用户子载波的信道质量为基础,依次从可用的子载波中挑选出符合需求的子载波.该算法的复杂度较低,但选择顺序靠后的用户会因剩余可选择的子载波越来越少而不得不选择一些信道质量较低的子载波,从而导致误码率偏高.文献[10]提出的最差用户优先(WUF)贪婪算法,允许平均信道质量最差的用户优先选择子载波,但性能提升非常有限.文献[11] 提出了最大贪婪算法,将用户以不同的方式排序,然后以最佳误码性能决定最终的子载波分配方案,该算法显著地提高了误码性能,但复杂度高.文献[12]首先利用普通贪婪算法实现初始分配,再通过交换任意2个用户的子载波来实现误码性能的提高.当子载波数量很大时,该算法的计算复杂度也将变得非常高.

在现有的功率分配方式中,平均功率分配算法计算量小,但由于不考虑信道增益的变化,当信道平均信道质量较低时,吞吐量小.注水算法研究目前主要集中在如何减少迭代次数和寻求运算量小的次优解[13-15].文献[15]给出了一种快速迭代算法.文献[16-17]研究了功率约束下系统吞吐量最大化时的功率分配问题,给出了在高信噪比(SNR)限定条件下用户间速率成比例的线性功率分配算法,但这种算法过于苛刻,只有当平均SNR大于25 dB时才能正常工作.

本文提出了一种适用于OFDMA系统的低复杂度的子载波-功率分配方案.子载波分配是一种改进的最差子载波避免(WSA)算法;而功率分配则是采用改进的线性注水算法.

1 系统模型

本文考虑的OFDMA系统模型需要实现为Q个用户合理分配M个子载波.对于多用户OFDMA系统而言,由于传播路径不同,对于某一用户严重衰落的子载波对其他用户却可能有较高的信道响应增益.因此,在认知OFDMA中采用适当的子载波分配算法,可以实现信道资源的充分利用.当完成子载波分配后,多用户的资源分配问题就转化为单用户的功率分配问题,即为每个子载波选择合适的发送功率,实现总用户吞吐量的最大化.

根据香农公式,第m个子载波的吞吐量可表示为[15]

(1)

(2)

因此,在总功率约束条件下,以用户吞吐量最大化为目标的分配优化问题可描述为

Pu(q,j)≥0 ∀q,j

Pd(q,j)≥0 ∀q,j

ρq,j={0,1} ∀q∈Θ,j∈Oq

(3)

2 资源分配算法

2.1 子载波分配

提出的子载波分配算法旨在将M个子载波分配给Q个用户时,每个用户可分配到K个子载波用来传输数据流,且确保每个用户分配到的子载波信道质量值{Gq,j}q∈Θ,j∈Oq尽可能大.

在以速率自适应(RA)准则的多用户子载波功率分配模型中,虽然为所有用户都分配对应信道质量最好的子载波很难实现,但避免将信道质量最差的子载波分配给该用户却相对容易.WSA算法[17]将每个子载波对应不同用户的信道质量值从小到大排序,其中最小值对应的用户优先选择所需子载波.即最小值Gq1,j1为第j1个子载波对应用户q1的信道质量,则第j1个子载波最先被分配给该子载波对应信道质量最高的用户;次小值Gq2,j2(已被分配的子载波对应的信道质量都不再参与排序)所在的第j2个子载波被分配给其第j2个子载波对应信道质量最高的用户;以此类推.

虽然WSA算法能有效避免用户被分配到较低信道质量的子载波,但依然有可能存在一种恶劣情况,即最后未被分配的子载波恰好只能被分配给对应信道质量最差的用户.为解决这一问题,本文提出了一种新的算法,基于方差降序的最差子载波避免(VDWSA)算法.VDWSA算法的基本思想是:将子载波按照其信道质量的方差降序排列并优先选择信道质量好的用户.VDWSA算法的具体步骤如下:

① 从M个子载波的Q×M个信道质量值中筛选出最小值Gq1,j1,并将Gq1,j1所在子载波调至首位.

② 求出剩余每个子载波信道质量的方差,并按照方差由大到小的顺序将剩余子载波依次排列在Gq1,j1所在子载波之后,若方差相同,则选出的对应不同用户的信道质量最小值较小的子载波优先排序.

③ 按照重新排序的子载波顺序依次将子载波分配给该子载波对应信道质量最优的用户,当某个用户被分配的子载波数达到K时,则该用户将不再参与后续的分配.

④ 当所有用户被分配的子载波数都等于K时,子载波分配结束.

2.2 功率分配

当子载波分配完成后,优化问题就变成功率分配问题.平均功率分配算法是最简单、计算量最小的功率分配算法.平均功率分配算法的计算公式为Pm=P/M.本文探讨了以平均功率分配为基础的迭代注水功率分配算法和线性注水功率分配算法.

注水功率分配算法的基本原理是,根据每个子载波的信道质量来分配功率,质量高的多分,质量低的少分甚至不分.其中,注水水位的主要作用是确定不分配功率的子载波.事实证明,只要能确定不分配功率的子载波,在剩余子载波中即使采用平均功率分配算法,也能明显提高用户的总吞吐量.式(3)的极大值优化问题可分为上行链路和下行链路2个独立的问题.首先考虑上行链路,利用拉格朗日乘数法可知,最优功率分配应满足如下必要条件:

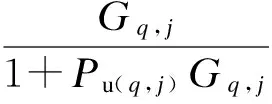
(4)

由式(4)可得

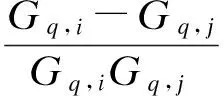
(5)

由式(5)可知,只要能确定某一个子载波的上行功率,就可以由它求出剩余子载波的上行功率,且每个用户的所有子载波的上行功率和为

(6)

由式(3)的约束条件可知PQ≤Pq,则有

(7)

由式(7)可求出各个子载波的上行功率,但此时求出的功率却可能无法满足式(3)中的另一个约束条件Pu(q,j)≥0.若求出Pu(q,j)<0时取Pu(q,j)=0,则会导致PQ>Pq,同样不能满足式(3)的约束条件.

(8)

若Pu(1,1)≤0,则令Pu(1,1)=0并去除该子载波.然后根据下式计算第2个子载波上行功率：

(9)

直到找出Pu(1,l)>0,然后根据式(5)求出余下子载波的上行功率.其余用户的上行功率计算方法相同.这种算法称为线性注水功率分配算法.该算法避免了迭代注水算法每次求出所有子载波功率后再修正β重新计算,可减少运算量,且避免了不切实际的约束条件.

然而,所有的注水算法均无法保证用户间的公平性.在CR系统中,SUs过高的传输功率,很可能对PUs产生干扰,影响PUs正常工作.因此,本文对原有的线性注水算法进行改进,新增了一个主用户抗干扰阈值Iu(q,j)=Pu(q,j)FSP(q,j),其中,FSP(q,j)为次用户q在第j个子载波上对主用户造成的干扰因子,可以计算得

(10)

式中,Hq,j为次用户q在第j个子载波上的信噪比;FPS(q,l,j)为主用户l在第j个子载波上对次用户q造成的干扰因子(为方便讨论,本文假设只有1个主用户,即L=1).

由线性注水算法计算出的次用户q对应的第k个子载波的上行功率为Pu(q,k),若Pu(q,k)>Iu(q,k),则该用户对应的第k个子载波的上行功率改为Iu(q,k),若Pu(q,k)≤Iu(q,k),则该用户对应的第k个子载波的上行功率仍为Pu(q,k)不变.

下行链路的传输功率算法与上行链路的传输功率算法类似.

3 复杂度分析

在子载波分配算法中,Greedy算法只需要为所有用户按序找到可用子载波的最大值,比较次数为M(M-1)/2,相应的计算复杂度为O(M2).Ring算法的第1阶段与Greedy算法类似,是对所有用户的所有子载波增益进行排序,采取顺序循环的选择方式并没有改变比较次数,仍为M(M-1)/2.WUF算法还需要为Q个用户排序,所以其总比较次数为M(M-1)/2+2QlnQ,其计算复杂度为O(M2).已知采用二进制搜索算法在M个实数中选择最小值需要M-1次比较,而采用快速排序算法对M个实数进行排序需要的比较次数平均为2MlnM.因此,WSA算法的比较次数为2MQ+2MlnM,其计算复杂度为O(MQ),其中Q≥lnM.同理,本文提出的VDWSA算法也需要通过M-1次比较在M个实数中选出最小值,并对M-1个实数进行排序,共需要比较次数 2MQ+M-1,其计算复杂度也为O(MQ).各子载波分配算法的具体计算复杂度对比见表1(其中,M≫Q).

表1 子载波分配算法的计算复杂度对比

由表1可看出,当子载波数较大时,Greedy算法、Ring算法和WUF算法的迭代次数要远远大于WSA算法和VDWSA算法,并且迭代次数之差随着子载波数的增加有逐步增大的趋势.这表明,WSA算法和VDWSA算法的执行时间较少,实时性更好.

在功率分配算法中,多用户迭代注水功率分配算法需要2nM次加法运算和n(M+2)次乘法运算,相应的计算复杂度为O(nM),其中n为所需的迭代次数.对于单用户系统的线性注水功率分配算法来说,其计算复杂度为O(Mlog2M),而多用户系统在功率分配前已完成了子载波向用户的分配,功率分配不需要再重复排序这一步骤,因此只需要2M-L+LM次加法运算和2+L次乘法运算,计算复杂度为O(LM),其中L为功率是0的子载波个数.而增加了主用户抗干扰阈值的线性注水功率分配算法由于需要将每个已分配的功率值与抗干扰阈值对比,因此增加了X次乘法运算,其中X为功率值大于抗干扰阈值的子载波个数.各功率分配算法的具体计算复杂度对比见表2,其中n≫L,M≫Q,M≫L,M≫X.

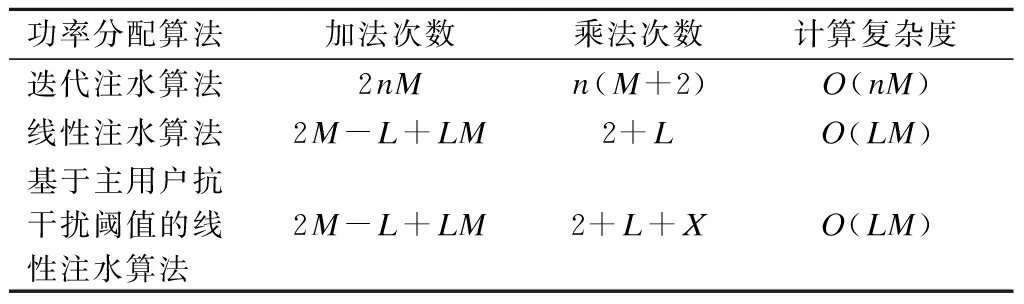
表2 功率分配算法的计算复杂度对比

4 仿真结果

设在一个OFDMA系统中,有Q=3个用户共享M=6个子载波,这样每个用户可以分配到K=2个子载波用来传输数据流.被分配的信道质量之和、均值、最大值和最小值(取1 000次仿真结果的平均值)如表3所示.

表3 不同子载波分配算法的结果统计

计算结果表明,本文所提出的VDWSA算法的子载波分配结果中最差信道质量值和平均信道质量值都要高于其他算法.因此,本文算法无论是从时效性,还是从子载波信道质量选择,其性能都要优于文献[10]提出的WUF算法和文献[14]提出的WSA算法,具有最优的综合性能.

考虑一个OFDMA系统,其中用户数Q=3,子载波数M=6,9,12,15,…,237,240,总授权带宽B=1.2 MHz,噪声功率N0=1.0×10-6W,每个用户允许的最大上行功率P1=P2=…=PQ=10 W,所有用户允许的最大下行功率P=100 W.假设信道为瑞利衰落,并伴随着对数方差为10 dB的阴影衰落.由于信道增益的不确定性,以下仿真结果均是以1 000次Monte Carlo仿真结果求平均所得.

图1给出了不同子载波分配算法在不同子载波数下的最差子载波信道质量比较.可以看出,VDWSA算法的最差子载波信道质量远高于Greedy算法和Ring算法,且略高于WSA算法和WUF算法.

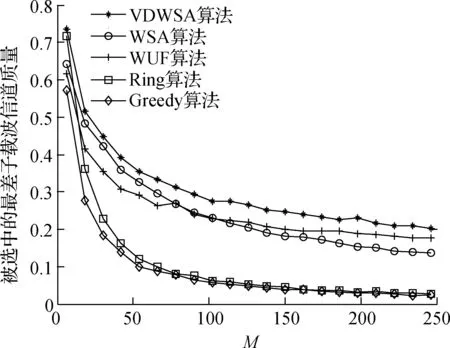
图1 不同子载波分配算法的最差子载波信道质量

本文以平均功率分配时的用户吐量为基准,比较各种注水功率分配算法的用户吞吐量.图2给出了不同功率分配算法在不同子载波数下的上行和下行链路平均用户吞吐量.由图2可见,在子载波分配算法相同时,本文提出的基于主用户抗干扰阈值的线性注水功率分配算法的用户吞吐量明显高于平均功率分配算法和迭代功率分配算法,且逼近文献[19]提出的原始线性注水算法,并有效地减少了次用户对主用户的干扰.

(a) 上行链路

(b) 下行链路

5 结论

1) 本文提出的资源分配方案适用于采用OFDMA的CR系统进行子载波与功率的分配.在进行子载波分配时,基于最差子载波避免的方差降序算法在保证低计算复杂度的前提下,有效地提高了被分配子载波的最差信道质量,从而避免因用户分配到信道质量不佳的子载波而导致误码率性能下降的问题.

2) 在进行功率分配时,由于已完成对各个用户的子载波分配,因此,基于主用户抗干扰阈值的线性注水算法可在用户内部完成对各子载波的功率分配,有效减小了运算量.

3) 该资源分配算法明显地提高了总用户吞吐量.仿真结果表明,用户吞吐量接近于传统线性注水算法的性能上限,且有效减少了次用户对主用户的干扰,实现了用户间的公平性.

)

[1] Tanab M E, Hamouda W. Resource allocation for underlay cognitive radio networks: A survey[J].IEEECommunicationsSurveys&Tutorials, 2017,19(2): 1249-1276. DOI: 10.1109/comst. 2016. 2631079.

[2] Tsiropoulos G I, Dobre O A, Ahmed M H, et al. Radio resource allocation techniques for efficient spectrum access in cognitive radio networks[J].IEEECommunicationsSurveys&Tutorials, 2016,18(1): 824-847. DOI: 10.1109/comst. 2014. 2362796.

[3] Yang Y, Park L T, Mandayam N B, et al. Prospect pricing in cognitive radio networks[J].IEEETransactionsonCognitiveCommunicationsandNetworking, 2015,1(1): 56-70. DOI: 10.1109/tccn. 015.2488636.

[4] Alfa A S, Maharaj B T, Lall S, et al. Mixed-integer programming based techniques for resource allocation in underlay cognitive radio networks: A survey[J].JournalofCommunicationsandNetworks, 2016,18(5): 744-761. DOI: 10.1109/jcn.2016.000104.

[5] Hu H, Zhang H, Liang Y C. On the spectrum- and energy-efficiency tradeoff in cognitive radio networks[J].IEEETransactionsonCommunications, 2016,64(2): 490-501. DOI: 10.1109/tcomm.2015.2505281.

[6] Mokari N, Parsaeefard S, Azmi P, et al. Robust ergodic uplink resource allocation in underlay OFDMA cognitive radio networks[J].IEEETransactionsonMobileComputing, 2016,15(2): 419-431. DOI: 10.1109/tmc.2015.2413782.

[7] Zhou F, Beaulieu N C, Li Z, et al. Energy-efficient optimal power allocation for fading cognitive radio channels: Ergodic capacity, outage capacity, and minimum-rate capacity[J].IEEETransactionsonWirelessCommunications, 2016,15(4): 2741-2755. DOI: 10.1109/twc. 015. 2509069.

[8] Chopra S, Notarstefano G, Rice M, et al. Distributed version of the Hungarian method for a multirobot assignment[J].IEEETransactionsonRobotics, 2017,99: 1-16. DOI: 10.1109/tro.2017.2693377.

[9] Fahmi A, Astuti R P, Meylani L, et al. Utilizing mean greedy algorithm using user grouping for chunk allocation in OFDMA systems with carrier aggregation[C]//2015 9thInternationalConferenceonTelecommunicationSystemsServicesandApplications(TSSA). Bandung, Indonesia, 2015: 1-4. DOI: 10.1109/tssa. 2015. 7440438.

[10] Basaran S T, Kurt G K, Engin B, et al. Joint power and subcarrier allocation in OFDMA systems[C]//2015 23rdSignalProcessingandCommunicationsApplicationsConference(SIU). Malatya, Turkey, 2015: 2170-2173. DOI: 10.1109/siu.2015.7130303.

[11] Nam C, Joo C, Bahk S. Joint subcarrier assignment and power allocation in full-duplex OFDMA networks[J].IEEETransactionsonWirelessCommunications, 2015,14(6): 3108-3119. DOI: 10.1109/twc.2015.2401566.

[12] Yin S, Qu Z. Resource allocation in multiuser OFDM systems with wireless information and power transfer[J].IEEECommunicationsLetters, 2016,20(3): 594-597. DOI: 10.1109/lcomm. 2016.2516999.

[13] Sboui L, Rezki Z, Alouini M S. Energy-efficient power allocation for underlay cognitive radio systems[J].IEEETransactionsonCognitiveCommunicationsandNetworking, 2016,1(3): 273-283. DOI: 10.1109/tccn.2015.2488622.

[14] Rawat D B, Bajracharya C. Channel and power adaptation for cognitive radios in multiuser OFDM systems[C]//2016IEEERadioandWirelessSymposium(RWS). Austin, TX, USA, 2016:129-132. DOI: 10.1109/rws. 2016. 7444384.

[15] Liu F, Yang Q, Gong P, et al. Subcarrier and power allocation for multi-user OFDMA wireless networks under imperfect channel state information[J].IETCommunications, 2016,10(8): 873-881. DOI: 10.1049/iet-com.2015.0711.

[16] Araniti G, Condoluci M, Iera A, et al. A low-complexity resource allocation algorithm for multicast service delivery in OFDMA networks[J].IEEETransactionsonBroadcasting, 2014,60(2): 358-369. DOI: 10.1109/tbc. 2014. 2321678.

[17] Chen Y, Zheng Z, Li Y, et al. Energy-efficient resource allocation in multiuser OFDM systems with proportional rate constraints[J].ElectronicsLetters, 2015,51(20): 1611-1613. DOI: 10.1049/el.2015.2111.

[18] Zhang D M. Linear water-filling power allocation algorithm in OFDMA system[J].JournalofElectronics&InformationTechnology, 2007,29(6): 1286-1289.

[19] Liu T, Yang C, Yang L L. A low-complexity subcarrier-power allocation scheme for frequency-division multiple-access systems[J].IEEETransactionsonWirelessCommunications, 2010,9(5): 1564-1570. DOI: 10.1109/twc. 2010. 5463212.

Alow-complexityresourceallocationalgorithmforOFDMAcognitivenetworks

Song Xiaoqin1Liu Ye1Jin Hui1Lei Lei1Hu Jing2Song Tiecheng2

(1College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China) (2School of Information Science and Engineering, Southeast University, Nanjing 210096, China)

For the power-limited orthogonal frequency division multiple access(OFDMA) cognitive networks, a low-complexity resource allocation algorithm is proposed, including subcarrier allocation and power allocation. In the subcarrier allocation, the algorithm assigns the subcarriers with the worst channel quality to the users at a higher priority. Then, the remaining subcarriers are sorted in descending order according to the variance of channel quality and assigned to the users. Thus, the remaining subcarriers will not be allocated to the users with the worst channel quality. In the power allocation, the judgment of the anti-interference threshold of the primary user is introduced into the traditional linear water-filling algorithm. This algorithm can maximize the throughput of secondary users and improve the anti-interference ability of the primary user simultaneously. The simulation results show that, compared with the existing algorithms, the proposed algorithm can effectively improve the channel quality for the subcarriers allocated to users. The throughput of secondary users is very close to the theoretical upper bound. The proposed algorithm has an acceptable fairness for primary users and low computational complexity.

orthogonal frequency division multiple access (OFDMA); subcarrier allocation; power allocation; user throughput

10.3969/j.issn.1001-0505.2017.06.007

TN914.5

A

1001-0505(2017)06-1123-06

2017-06-05.

宋晓勤(1973—)，女，博士，副教授，xiaoqin.song@163.com.

国家自然科学基金资助项目(61372104，61572254)、研究生创新基地(实验室)开放基金资助项目(kfjj20170402).

宋晓勤,刘叶,金慧,等.一种用于OFDMA认知网络的低复杂度资源分配算法[J].东南大学学报(自然科学版),2017,47(6):1123-1128.

10.3969/j.issn.1001-0505.2017.06.007.