基于图优化的单目线特征SLAM算法

董蕊芳 柳长安 杨国田 程瑞营

(华北电力大学控制与计算机工程学院, 北京 102206)

基于图优化的单目线特征SLAM算法

董蕊芳 柳长安 杨国田 程瑞营

(华北电力大学控制与计算机工程学院, 北京 102206)

提出了基于图优化的单目线特征同时定位和地图构建(SLAM)的方法.首先,针对主流视觉SLAM算法因采用点作为特征而导致构建的点云地图稀疏、难以准确表达环境结构信息等缺点,采用直线作为特征来构建地图．然后,根据现有线特征的SLAM算法都是基于滤波器的SLAM框架、存在线性化及更新效率的问题,采用基于图优化的SLAM解决方案以提高定位精度及地图构建的一致性和准确性．将线特征的Plücker坐标和Cayley参数化方式相结合,一方面采用Plücker坐标便于线性投影计算,另一方面采用Cayley参数化方式有利于线特征参数的非线性优化．仿真实验结果显示：所提出算法的位姿估计误差平方和与均方根误差分别是里程计位姿估计的2.5%和10.5%,是基于EKF线特征SLAM算法估计位姿误差的22.4%和33%,重投影误差仅为45.5像素;实际图像实验中的位姿估计误差平方和为958 cm2,均方根误差为3.9 413 cm,从而证明了所提出算法的有效性和准确性.

单目SLAM;线特征;图优化;Plücker坐标;Cayley直线

机器人同时定位与地图构建(simultaneous localization and mapping,SLAM)是机器人实现完全自主移动的一项关键技术.该技术使机器人在未知环境移动过程中借助所携带的传感器实现对自身的定位,同时完成对周围环境的地图构建[1-2].视觉传感器具有体积小、成本低、易于安装、且包含丰富的环境信息等优点,因而被广泛应用于SLAM系统中[3].

传统的视觉SLAM算法主要是提取图像中的点作为特征进行制图和定位,构建的地图为点云地图,点特征易于提取，现有点特征描述算法及跟踪算法成熟,但稀疏的点云难以准确地描述周围环境的结构信息;与点特征相比,线特征广泛存在于各类环境场景中,由于直线比点高一个维度,其表示的地图能更加准确地表达环境的信息,尤其是对于结构化场景,如输电杆塔、工业建筑、铁路及室内走廊等,线特征具有明显的优势;此外,图像中线特征的匹配较点特征具有较好的光照不变性,且不易受视点变化的影响,更有利于进行回环检测[4-6].

线特征的参数化方法是研究基于线特征SLAM算法的基础,目前主要分为非线性最小维度4-参数表达方式以及线性冗余维度(over-parameters)参数化方式两大类.对于第1类参数化方法,Roberts[7]采用2个方向余弦结合1个2D坐标来表示空间直线的方向和位置;Ohwovoriole等[8]采用2个平面相交得到直线的表达方式;Zhang等[9]采用Cayley参数化方式.空间直线具有4个自由度,不存在冗余维度,也无需一致性约束,因此这类参数化方式能够更好地适用于非线性优化算法.然而,由于该类参数化方法的非线性,不合适于对线特征进行线性投影计算.

对于线性冗余维度参数化方法,文献[10-11]采用2个线段端点表示空间直线;Montiel等[12]采用线段的中点及方向向量表达空间直线.对于这2种参数化方式,线段的中点及2个端点在图像中都不能保证被稳定地检测到.Sola等[13]和Lemaire等[14]均采用Plücker坐标来表示直线,可以很方便地对线特征使用线性投影模型,但不利于进行非线性优化.

SLAM本质上是一个状态估计问题,其求解方法可大致分为基于滤波器的方法和基于图优化或基于平滑的方法.对于基于线特征的视觉SLAM,大部分都采用第一类方法,如文献[6,11,13-14]都采用扩展卡尔曼滤波方法,这类方法存在线性化及更新效率等问题,难以应用于大规模环境地图的创建[15].与滤波方法中每一步只考虑机器人当前位姿不同,基于平滑的方法通过所有的观测信息估计机器人完整的运动轨迹及地图,因而也被称为完全SLAM方法,地图的一致性和精度较好.近年来,该类方法在基于点特征的视觉SLAM中得到广泛的应用,但是基于线特征的视觉SLAM方法中则很少使用该类方法,文献[9]将SBA(sparse bundle adjustment)[16]应用到基于线特征的运动恢复结构(structure from motion,SfM)问题中.

综上,考虑到非线性最小维度4-参数表达方式以及线性冗余维度(over-parameters)的优点与不足,本文采用Plücker坐标与Cayley结合的线特征表达方式,一方面采用Plücker坐标便于线特征的线性投影计算,另一方面采用Cayley参数化方式有利于对线特征的位置进行非线性优化.由此提出了一种基于图优化的单目线特征SLAM算法,重点阐述线特征的参数化、初始化及图优化.

1 3D线特征的参数化方式

本文的线特征采用Plücker坐标结合Cayley参数化的方式,下面分别对这2种方式进行说明,并给出2种参数化方式间的相互转换方法,同时阐述了Plücker直线的初始化方法.

1.1 直线的Plücker坐标

假定直线上存在任意2点{A,B}∈R3,则该直线的Plücker坐标为一个6维向量L=(n;v),如图1所示,其中,世界坐标的原点为O,n为直线的矩向量,方向垂直于原点与该直线确定的平面η,幅值为OAB所组成三角形面积的2倍,v为直线的方向向量,由A指向B.该坐标可由下式进行计算:

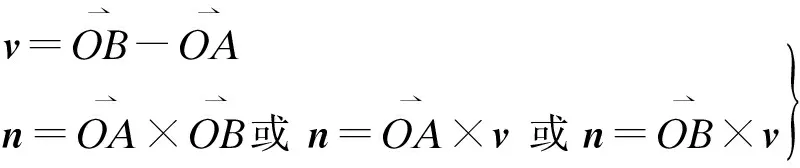
(1)

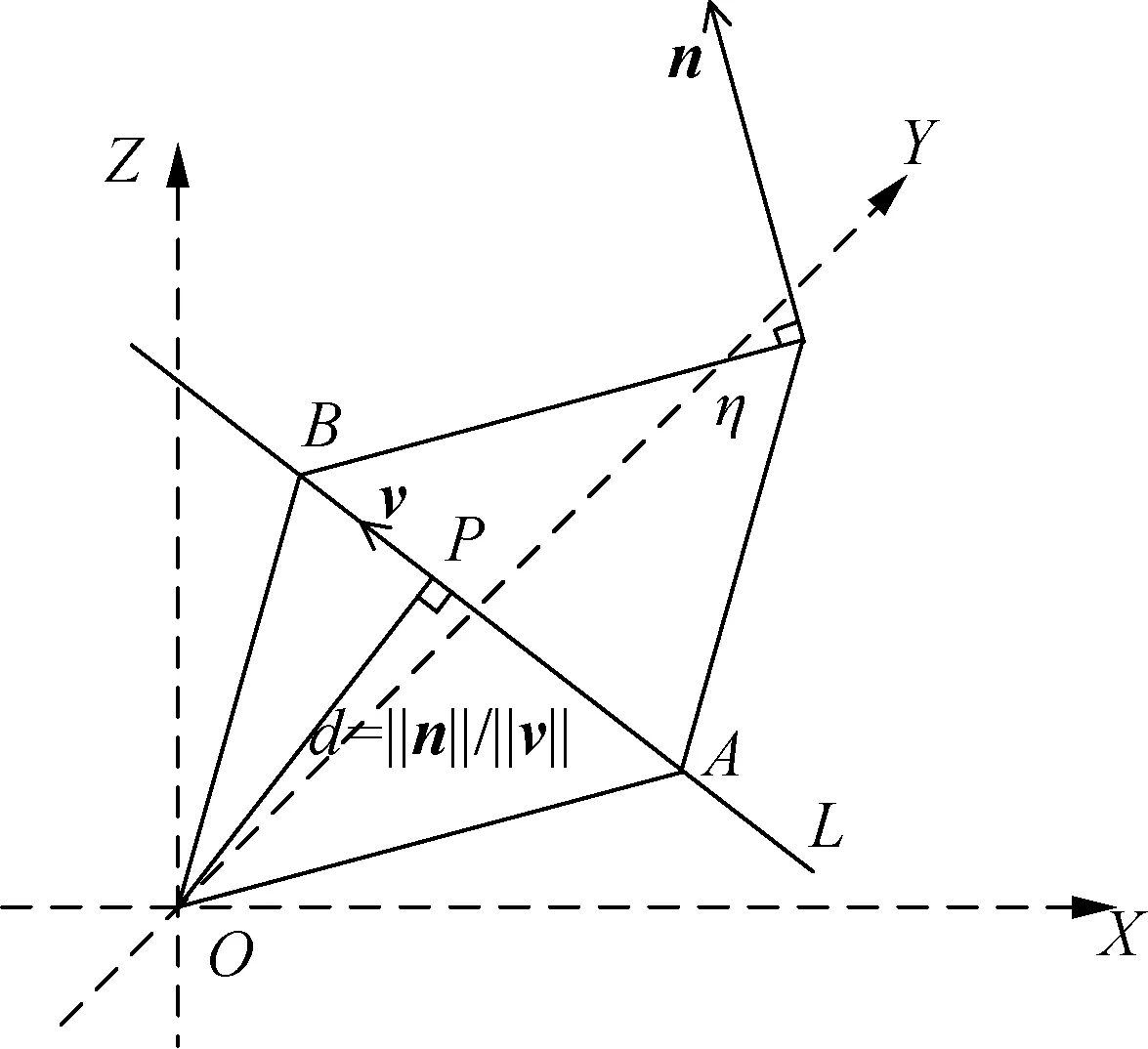
图1 Plücker直线

直线的Plücker坐标具有如下性质:

1) 满足Plücker约束v⊥n,即v·n=0;

1.1.1Plücker直线的坐标变换

令Lc表示Plücker直线在摄像机坐标系下的坐标,Lw表示Plücker直线在世界坐标系下的坐标,则直线在2个坐标系下的相互转换关系为

Lw=HLc

(2)

(3)

式中,t为相机中心在世界坐标系下的三维位置坐标;R为一个3×3的旋转矩阵,表示相机坐标系的朝向;H为变换矩阵.

将空间中的Plücker直线Lc投影到成像平面,得到直线l, 即

l=KRT(nw-t×vw)=Knc

(4)

(5)

式中,K为摄像机内参数矩阵；αv,αu为像素焦距；u0，v0为主点坐标．根据式(4)可知,经过投影变换后,直线Plücker坐标中仅nc是可观测的,而vc包含了直线的深度及方向信息,经过投影变换后都不可观测.

1.1.2 Plücker直线的位置初始化

单目SLAM问题是一个部分可观测的SLAM问题,从一幅图像中无法获得特征的完整位置信息,如线特征的深度及方向都无法通过单幅图像计算出来,因此存在特征位置的初始化问题.特征位置初始化过程是指通过图像中的特征观测信息来获得其3D位置信息.Sola等[17]提出了基于非迟延(undelayed)的初始化方法,并结合逆深度参数化[18]的方式对线特征进行了初始化,该方法的优点在于在低视差的情况下也依然有效,且与迟延(delayed)类的初始化方法相比,能够利用更多的特征信息.其初始化过程如下:

① 根据图像中检测到的线段z=(p1,p2),其中p1(p1x,p1y),p2(p2x,p2y)为线段在图像中的2个二维端点坐标,计算该线段在图像中的Plücker坐标l={l1,l2,l3}T,即

(6)

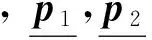
② 对l进行反投影变换,计算其所对应的3D Plücker直线坐标Lc,即

nc=K-1l

(7)

l的反投影过程如图2所示,但如前所述,Lc中只有nc子向量可测.

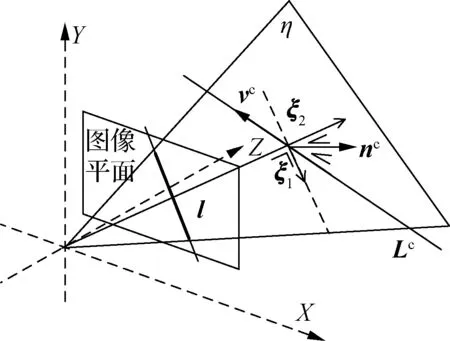
图2 图像中直线l的反投影示意图[13]

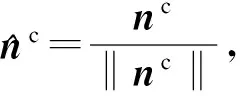
由图2可看出,l所对应的3D空间直线必定位于l与摄像机中心确定的平面η上,因此,只要构造一组平面η上的正交基ε={ξ1,ξ2},则向量vc便可由下式表示:

vc=β1ξ1+β2ξ2β1,β2∈R

(8)

(9)

式中,β={β1,β2}为对应ε的2个基方向系数,给定任意一组β都能得到一个向量vc⊂η,并且无论β取何值,都能满足Plücker约束v⊥n.

1.2 直线的Cayley表征方式

由于直线的Plücker坐标表示方式存在Plücker约束v⊥n,不利于后端的非线性优化过程．文献[9]指出该约束只能在线特征的初始化时满足,若直接使用Plücker坐标进行优化,则在优化过后无法保证该约束条件.因此,为了方便实现非线性优化过程,本文结合了直线的Cayley表征方式.

Cayley表达式定义为一个4维向量W=(d,s),其中,d表示直线到坐标系原点的距离,s={sx,sy,sz}T表示该直线在空间中的旋转信息,如图3所示.

以下为将Plücker直线L转换为Cayley直线

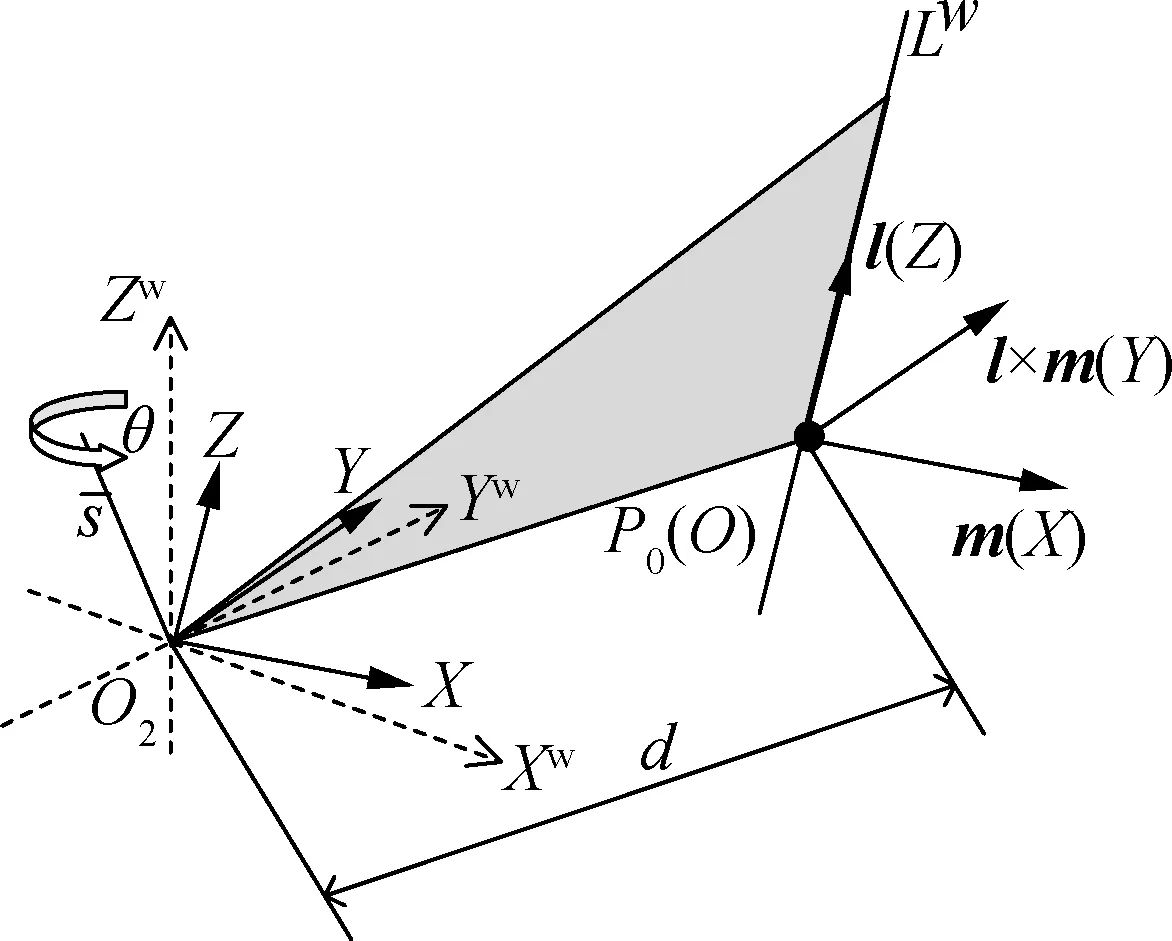
图3 3D直线的Cayley表示[9]

的过程.

① 根据下式计算出Plücker直线L上距离坐标原点最近点P0:

P0=(v×n)/‖v‖2

(10)

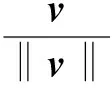
m=P0×vn

(11)

③ 按照下式构建正交矩阵Q:

(12)

根据下式计算出一个由向量s构成的反对称矩阵:

[s]×=(Q-I)(Q+I)-1

(13)

至此,Cayley直线的坐标表达式W=(d,s)已经求出,但当‖m‖=0时,该参数化方式容易存在奇异解,因此,需要进行修正以解决该问题,即

(14)

式中,i1,i2,vn为空间坐标系中的一组正交基,由约束(vn)T·i=0构建;τ为接近于0的一个无限小值.当‖m‖=0时,Q=[vn,i1,i2],从而解决了上述问题.

而将Cayley直线转换为Plücker直线的过程亦需要构造矩阵Q,可通过下式进行:

Q={q1,q2,q3}=(I-[s]×)-1(I+[s]×)=

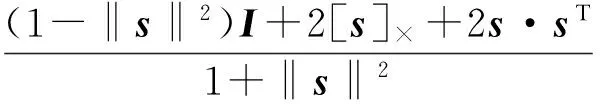
(15)

根据Q的定义(12)，可得Plücker直线坐标为

vn=q1m=dq2

(16)

2 基于线特征的单目SLAM后端优化

首先,对本文中的状态量做如下定义:

1)X={xi(Ri,Ti),i∈0,1,…,M}表示摄像机的一系列位姿;

2)Γ={Lj=(nj;vj),j∈1,2,…,N}表示一系列线特征的Plücker坐标;

3)W={Wj=(dj,sj),j∈1,2,…,N}表示一系列线特征的Cayley参数.

基于图优化的SLAM框架通常将求解过程分为前端和后端2个部分:前端完成图的构建，得到初始状态估计;后端对初始状态估计做进一步优化,得到位姿的最大似然估计．在基于图优化的视觉SLAM中,相机的位姿和路标的位置表示为图中的节点,观测信息在经过处理后转变为连接节点之间的约束,也称图中的边,本文采用因子图模型来描述SLAM问题.

2.1 优化中的误差模型

在SLAM优化问题中,主要用到相机的位姿预测误差模型和线特征的投影误差模型.

令ui(i∈1,2,…,M)表示相邻2帧间的控制输入量或测量得到的相对位姿,则位姿预测误差模型为

e(xi,xi-1)=xi-f(xi-1,ui)

(17)

式中,xi和xi-1表示相机在第i时刻和i-1时刻的位姿;f(xi-1,ui)表示相机的运动模型,通常情况下,该模型是非线性函数.

令zk(p1,p2),k∈1,2,…,K表示在图像中线特征测量值.与点特征不同的是,线特征的投影误差模型不再是简单的特征投影预测值与测量值之间的差,在本文中,线特征的误差计算模型为

(18)

式中,l={l1,l2,l3}T表示图像中线特征的预测值,由式(4)计算得到.式(18)为一个2维的向量e=(e1,e2),直观理解如图4所示．

图4 线特征的投影误差计算示意图

2.2 后端优化

SLAM可以看作是一个非线性最小二乘问题,在前端完成整个因子图的构建后,后端对目标函数进行优化,本文基于线特征的目标优化函数为

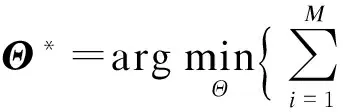
(19)

式中,Θ(X,Γ)为需要优化的状态量,X{xi},Γ{Lj};ei(xi-1,xi)为第i时刻的相机运动估计误差,通过式(17)计算;ek(xik,Ljk)为线特征的投影预测误差,通过式(18)计算;(xik,Ljk)为第k个测量相机在位姿xi处对Lj的观测;Ωi和Λk分别表示2个误差的协方差矩阵.

通过求解优化目标函数(19)，可得到一组最优的相机位姿X和特征位置Γ,使得所有Ljk在xik中的投影位置与zk尽可能靠近.求解目标函数(19)的过程也称为集束调整(bundle adjustment, BA)[19].Levenberg-Marquardt(LM)算法[20]是目前使用最广泛的非线性最小二乘问题求解方法,其独特的快速迭代性能和抑制局部最优解的能力在视觉SLAM模型中具有更快的效率和更准确的精度.因此本文采用该算法进行优化.

首先对式(19)中的误差项进行线性近似,近似方法与基于点特征的SLAM相同.但如前所述,线特征的投影误差模型较点特征复杂,因此近似过程中与线特征相关的Jacobian矩阵求解公式有所不同,线特征的参数更新过程亦不同,本文仅给出优化过程中与线特征相关的Jacobian矩阵求解方法.

线特征在投影过程中采用Plücker坐标,而优化更新过程采用Cayley参数化方式,此时投影误差对线特征的Jacobian矩阵J的求解过程为

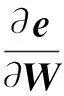
(20)

(21)

(22)

(23)

线特征的状态更新式为

Wj+1=Wj+δW

3 实验结果与分析

本文算法的实现中使用了GTSAM和MRPT两个库,系统配置为Windows 764位,12 GB内存,2.5 GHz主频,开发环境为Visual Studio 2013,用GTSAM库搭建SLAM框架,MRPT库实现可视化.

3.1 仿真实验

进行仿真实验方便将计算结果与真值进行对比,从而更好地评估实验结果．本文首先采用如图5(a)所示的仿真场景[21],一个由23根线段组成的简易房屋,实验中没有考虑遮挡,所有线条可见．所模拟的相机视场FOV为90°,图像尺寸为640×480像素,机器人以半径为5 m绕模型移动一圈．相机方向始终朝向房屋,共拍摄180帧图像．实验中对每一帧仿真图像中的线段端点坐标都添加了高斯噪声,还模拟了机器人的码盘定位,并为其添加高斯噪声,以此作为运动预测.

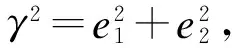
(a) 模拟简易房屋 (b) 重建后的房屋

图6 重建模型的重投影误差

图7为在相同噪声参数下,相机的真实运动路径、码盘估计路径、EKF线特征SLAM算法估计路径与本文算法估计的路径对比图.可以看出,使用本文SLAM方法的定位精度明显比基于EKF算法所估计结果的精度高,而且随着时间的推移，提高的程度越明显,而码盘估计有着严重的误差累积.表1量化了各算法估计的位姿误差平方和(SSE)和均方根误差(RMSE),从表中也可以看出本文算法较EKF与码盘估计的估计精度更高,且SSE和RMSE分别是里程计位姿估计的2.5%和10.5%,是基于EKF的线特征SLAM算法所估计位姿的22.4%和33%.

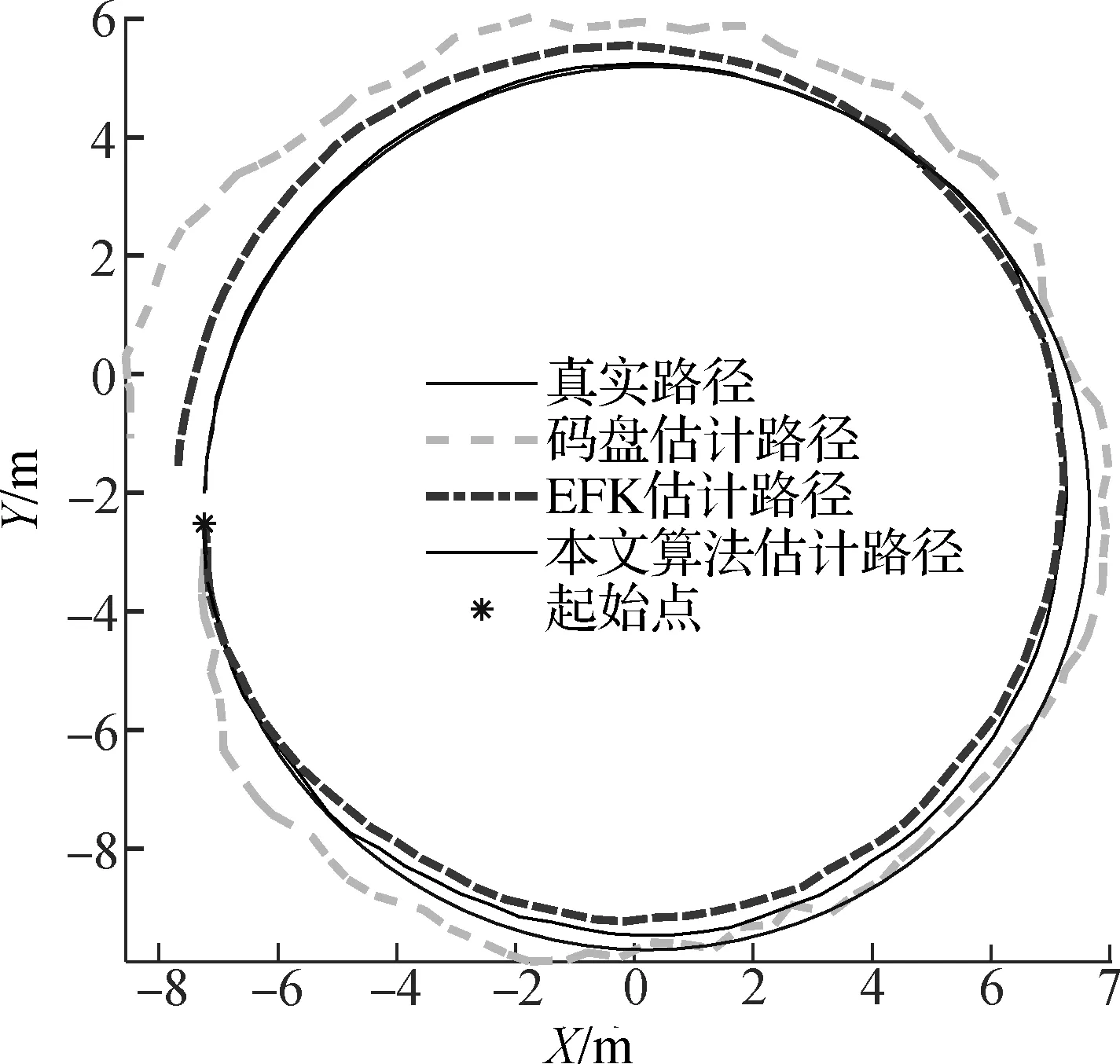
图7 运动估计结果对比

参数里程计EKF算法本文算法SSE/m24863.3540.8120.87RMSE/m5.22701.67320.5513

3.2 实际图像序列实验

在实际图像序列实验中,采用目前流行的LSD (line segment detector)算法[22]作为图像线特征的检测算法,同时采用LBD (line band descriptor)[23]算法进行线特征的匹配.LBD算法在弱纹理、部分遮挡、图像模糊、旋转和尺度变化等条件下都能够对线特征进行较好的匹配.

本文的视频序列图像采用Logitech C270进行采集,图像尺寸为640×480像素,实验场景如图8(a)所示,尺寸为120 cm×60 cm×60 cm,整个因子图中共有位姿节点60个,路标节点400个,约束1 860个,整个过程运行时间45 s.图8(b)为本文算法的重建结果,从图中可以看出,场景中的小电塔模型没有很好地构建出来,是因为该模型中的线条太短,算法中对线段的长度设置了阈值40像素,当图像中长度小于40像素的线段则不做处理;另外,场景中的笔筒及笔也没有很好地重建出来,是因为图像中该部分的线特征没有成功提取,因此建图的质量也依赖于图像中线特征提取和匹配算法的性能.综上,本文重建的线特征与场景基本一致,证明了本文算法的有效性.为了量化算法的精度,本文计算了所估计轨迹的误差平方和为958 cm2,均方根误差为3.941 3 cm,验证了本文算法的高定位精度.

(a) 真实场景

(b) 重建结果

4 结论

1) 传统的基于线特征的SLAM都采用基于滤波器的框架求解,本文采用基于图优化的SLAM解决方案来提高定位的精度及地图构建的一致性和准确性.

2) 本文结合了Plücker坐标和Cayley参数化方式来表征线特征,一方面采用Plücker坐标便于线性投影计算,另一方面采用Cayley方式有利于线特征位置的非线性优化,解决了线特征在图优化方案中的表征难题.

3) 通过仿真实验,将本文算法与码盘估计及EKF线特征SLAM算法进行了对比,结果显示本文算法的位姿估计误差平方和及均方根误差均小于码盘估计及EKF线特征SLAM算法结果,同时,计算了本文算法构建的线特征重投影误差,从结果看出伴随相机的运动,观测量越来越多,重投影误越来越小,从而说明本文算法具有较高的定位精度及建图精度.

4) 通过实际图像实验分析了位姿估计的误差平方和及均方根误差,结果证明了本文算法的有效性、准确性及地图构建的一致性.

)

[1] Cadena C, Carlone L, Carrillo H, et al. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age [J].IEEETransactionsonRobotics, 2016 ,32(6) :1309-1332.DOI:10.1109/TRO.2016.2624754.

[2] 段华旭,闫飞,庄严,等.无人车基于双目视觉的同时定位与地图构建[J].华中科技大学学报(自然科学版),2015,43(z1):319-323. DOI:10.13245/j.hust.15S1076.

Duan Huaxu, Yan Fei, Zhuang Yan, et al. Simultaneous localization and mapping for ugvs with binocular camera[J].JournalofHuazhongUniversityofScienceandTechnology(NatureScienceEdition), 2015,43(z1): 319-323. DOI:10.13245/j.hust.15S1076.(in Chinese)

[3] 刘浩敏,章国锋,鲍虎军.基于单目视觉的同时定位与地图构建方法综述 [J].计算机辅助设计与图形学学报,2016,28(6):855-868. DOI:10.3969/j.issn.1003-9775.2016.06.001.

Liu Haomin, Zhang Guofeng, Bao Hujun. A survey of monocular simultaneous localization and mapping [J].JournalofComputer-AidedDesign&ComputerGraphics, 2016,28(6): 855-868. DOI:10.3969/j.issn.1003-9775.2016.06.001. (in Chinese)

[4] 周慧中.基于结构线条的视觉 SLAM 方法[D].上海:上海交通大学电子信息与电气工程学院,2015.

[5] Zhao L, Huang S, Yan L, et al. A new feature parametrization for monocular SLAM using line features [J].Robotica, 2015,33(3):513-536.DOI:10.1017/S026357471400040X.

[6] Esparza-Jiménez O, Devy M, Gordillo J L. Visual EKF-SLAM from heterogeneous landmarks [J].Sensors, 2016,16(4): 489.

[7] Roberts K S. A new representation for a line [C]//ComputerSocietyConferenceonproceedingsoftheComputerVisionandPatternRecognition. Ann Arbor, MI, USA, 1988:635-640.

[8] Ohwovoriole M S, Roth B. An extension of screw theory [J].JournalofMechanicalDesign, 1981,103(4):725-735. DOI:10.1115/1.3254979.

[9] Zhang L, Koch R. Structure and motion from line correspondences: Representation, projection, initialization and sparse bundle adjustment [J].JournalofVisualCommunicationandImageRepresentation, 2014,25(5): 904-915. DOI:10.1016/j.jvcir.2014.02.013.

[10] Smith P, Reid D, Davison A. Real-time monocular SLAM with straight lines [C]//ProceedingsoftheBMVC. Edinburgh, UK, 2006:17-26. DOI:10.5244/c.20.3.

[11] Gee A P, Mayol-Cuevas W. Real-time model-based SLAM using line segments [C]//ProceedingsoftheInternationalSymposiumonVisualComputing. Berlin, Heidelberg: Springer, 2006:354-363. DOI:10.1007/11919629_37.

[12] Montiel J M M,Tardós D, Montano L. Structure and motion from straight line segments [J].PatternRecognition, 2000,33(8):1295-1307. DOI:10.1016/s0031-3203(99)00117-x.

[13] Sola J, Vidal-Calleja T, Civera J, et al. Impact of landmark parametrization on monocular EKF-SLAM with points and lines [J].InternationalJournalofComputerVision, 2012,97(3):339-368.

[14] Lemaire T, Lacroix S. Monocular-vision based SLAM using line segments [C]//ProceedingsoftheProceedings2007IEEEInternationalConferenceonRoboticsandAutomation. Roma,Italy, 2007:2791-2796. DOI:10.1109/robot.2007.363894.

[15] 梁明杰,闵华清,罗荣华.基于图优化的同时定位与地图创建综述[J].机器人,2013,35(4):500-512. DOI:10.3724/SP.J.1218.2013.00500.

Liang Mingjie, Min Huaqing, Luo Ronghua. Graph-based SLAM: A survey [J].Robot, 2013,35(4): 500-512. DOI:10.3724/SP.J.1218.2013.00500. (in Chinese)

[16] Lourakis M I A, Argyros A A. SBA: A software package for generic sparse bundle adjustment [J].ACMTransactionsonMathematicalSoftware(TOMS), 2009,36(1):2-1-2-30.

[17] Sola J, Vidal-Calleja T, Devy M. Undelayed initialization of line segments in monocular SLAM [C]//Proceedingsofthe2009IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems. Louis, USA,2009: 1553-1558. DOI:10.1109/iros.2009.5354754.

[18] Civera J, Davison A J, Montiel J M. Inverse depth parametrization for monocular SLAM [J].IEEETransactionsonRobotics, 2008,24(5): 932-945. DOI:10.1109/tro.2008.2003276.

[19] Triggs B, Mclauchlan P F, Hartley R I, et al. Bundle adjustment—A modern synthesis [C]//ProceedingsoftheInternationalWorkshoponVisionAlgorithms. London, UK: Springer Springer-Verlag, 2000:298-372.

[20] Ranganathan A. The levenberg-marquardt algorithm [J].TutoralonLmAlgorithm, 2013,11(1):101-110.

[21] Solà J. Slam toolbox for matlab[EB/OL]. (2015-12)[2017-08].http://www.iri.upc.edu/people/jsola/JoanSola/eng/toolbox.html.

[22] von Gioi R G, Jakubowicz J, Morel J-M, et al. LSD: A line segment detector [J].ImageProcessingonLine, 2012,2:35-55. DOI:10.5201/ipol.2012.gjmr-lsd.

[23] Zhang L, Koch R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency [J].JournalofVisualCommunicationandImageRepresentation,2013,24(7):794-805.DOI:10.1016/j.jvcir.2013.05.006.

Line-basedmonoculargraphSLAMalgorithm

Dong Ruifang Liu Changan Yang Guotian Cheng Ruiying

(School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China)

A new line based 6-DOF monocular algorithm for using graph simultaneous localization and mapping(SLAM) algoritm was proposed. First, the straight line were applied as a feature instead of points, due to a map consisting of a sparse set of 3D points is unable to describe the structure of the surrounding world. Secondly,most of previous line-based SLAM algorithms were focused on filtering-based solutions suffering from the inconsistent when applied to the inherently non-linear SLAM problem, in contrast, the graph-based solution was used to improve the accuracy of the localization and the consistency of mapping. Thirdly, a special line representation was exploited for combining the Plücker coordinates with the Cayley representation. The Plücker coordinates were used for the 3D line projection function, and the Cayley representation helps to update the line parameters during the non-linear optimization process. Finally, the simulation experiment shows that the proposed algorithm outperforms odometry and EKF-based SLAM in terms of the pose estimation, while the sum of the squared errors (SSE) and root-mean-square error (RMSE) of proposed method are 2.5% and 10.5% of odometry, and 22.4% and 33% of EKF-based SLAM. The reprojection error is only 45.5 pixels. The real image experiment shows that the proposed algorithm obtains only 958 cm2and 3.941 3 cm the SSE and RMSE of pose estimation. Therefore, it can be concluded that the proposed algorithm is effective and accuracy.

monocular slam; line feature; graph optimization; Plücker coordinates; Cayley representation

10.3969/j.issn.1001-0505.2017.06.003

TP242

A

1001-0505(2017)06-1094-07

2017-07-23.

董蕊芳(1989—),女,博士生;柳长安(联系人),男,博士,教授,博士生导师,liuchangan@ncepu.edu.cn.

国家自然科学基金资助项目(61105083)、中央高校基本科研业务费专项资金资助项目(2015XS63).

董蕊芳,柳长安,杨国田,等. 基于图优化的单目线特征SLAM算法[J].东南大学学报(自然科学版),2017,47(6):1094-1100.

10.3969/j.issn.1001-0505.2017.06.003.