黏弹性层状周期板动力计算的近似理论与解答
徐司慧 王炳龙 周顺华 杨新文 李尧臣
*(同济大学道路与交通工程教育部重点实验室,上海201804)
†(同济大学航空航天与力学学院,上海200092)
黏弹性层状周期板动力计算的近似理论与解答
徐司慧*,1)王炳龙*周顺华*杨新文*李尧臣†
*(同济大学道路与交通工程教育部重点实验室,上海201804)
†(同济大学航空航天与力学学院,上海200092)
由于周期性隔振结构动力计算中较少考虑轨道交通载荷及材料黏弹性,因此,本文以黏弹性层状周期板为研究对象,提出了垂向移动简谐载荷下,可以考虑材料黏弹性及板内横向剪切变形的黏弹性层状周期板动力计算近似理论并给出解析解答.设板中性面的横向剪切变形为横截面的整体剪切变形,利用Reissner-Mindlin假设及提出的剪切变形补充计算条件,得到了中性面法线转角与中性面剪应力的关系.基于平衡方程和应力连续条件,建立了黏弹性层状周期板振动控制方程,推导了对边简支对边自由条件下,板垂向位移的简化Fourier级数形式解.与经典层合板模型和有限元计算结果进行了比较,验证了本文解答的有效性.结果表明:(1)黏弹性层状周期板可以显著降低单一材料板在自振频率处的振动响应,但会引起局部低频频段的振动放大;(2)板的垂向位移随着载荷速度的增大而增大,当载荷速度超过300km/h后,其对板振动响应的影响减弱;(3)黏弹性层剪切模量存在最佳设计值,可使结构的隔振性能最佳;(4)黏弹性层的阻尼特性在低频范围内对结构振动影响较小;(5)可在满足工程实际的情况下适当增加板长,以提高结构的隔振性能.
周期性结构,轨道交通载荷,Reissner-Mindlin假设,解析解,振动响应
引言
周期性结构是指由基本周期单元按照相同的排列方式在单方向或多方向上堆积而成的结构[1-2].固体物理学研究表明,周期性结构具有独特的频率衰减域特性,即处于某些频段(衰减域)的波不能顺利透过该结构,导致振动减弱[3-5].受此启发,石志飞等[6-8]于2007年将周期性的结构引入土木工程领域,提出了周期性隔震基础和周期性排桩等,隔震/振效果显著,为周期性结构在实际工程中的应用打下了基础.
目前,研究较广泛的周期性隔震/振基础主要为在单方向上呈周期性排列的层状周期板,这也是周期性结构的基本形式.研究内容集中于地震载荷下的建筑物隔震技术,采用的理论和方法主要有传递矩阵法、有限元法、模型试验等.石志飞等[9]利用传递矩阵法研究了地震载荷作用下层状周期板基础的动力衰减域特性,得到了衰减域的主要控制因素;黄建坤[10]采用平面波展开法研究了周期性排桩和波屏障在环境减振中的应用,并设计出了具有隔振效果的波屏障;陈志宝等[11-12]通过振动台试验证明了具有黏弹性的层状周期结构对外部激励具有较好的隔离或减弱效果.上述研究虽然取得了一系列有益成果,但是载荷形式较单一,多为地震载荷,较少涉及工程中广泛存在的轨道交通载荷,难以体现载荷的作用范围以及移动速度.
轨道交通载荷是轨道交通结构振动的主要振源,研究轨道交通载荷下的结构减振技术对轨道交通领域的环境振动控制意义重大.本文将周期性结构应用于轨道交通减振领域,采用黏弹性层状周期板作为轨道交通领域板结构的基本形式.为了考虑轨道交通载荷及材料的黏弹性,采用经典轨道动力学中轮轨垂向作用力的基本形式,即垂向移动简谐载荷[13-14],并将具有黏弹性的层状周期板视为复合材料层合板结构,利用层合板理论进行动力计算.从既有文献的调研结果来看,求解层合板问题常采用基于Kirchho ff假设的经典板理论[15],即将每层板视为不考虑横向剪应力的薄板,然后联立求解.然而,由于忽视了板内横向剪应力,经典层合板理论无法考虑板的面内位移在板厚方向上的zig-zag效应以及层间剪应力连续条件[16-18],因此无法准确计算板面的挠度分布,难以预测层状周期板的减振效果.
基于经典层合板理论,学者从优化剪切函数、细化应力场分布等角度提出了多个复合材料层合板理论[19-21].Chen等[22-23]采用三维弹性理论得到了对边简支层合板的自由振动半解析解.Yang等[24]利用高阶变形理论对夹芯板的受迫振动进行了分析.Faruk Firat Calim[25]在拉氏域内分析了非均匀复合材料梁的自由振动和强迫振动,研究了非均匀参数对梁动力特性的影响.Ganapathi等[26]引入材料特性剪切修正因子,结合一阶剪切变形理论建立了层合板的振动方程.李尧臣等[27-28]利用简化理论对压电功能梯度圆板和矩形板进行了分析并得到了近似解析解.Thai等[29]基于一阶剪切变形板理论来计算夹芯板的力学特性并得到了很好的结果.Pandey和Pradyumna[30]利用Layerwise理论对功能梯度夹芯板的自由振动问题进行分析.一般认为,复合材料层合板理论可以得到简单边界条件下较为精确的结构整体响应,比如挠度、基频振动频率等.然而,由于独立场变量的个数随层合板铺层数的增加而增加,导致该类方法计算量较大,不适用于大规模工程问题的计算.因此,针对黏弹性层状周期板,探索表达形式和算法相对简洁,同时精度又能满足要求的近似理论很有必要.
本文将周期性结构应用于轨道交通减振领域,采用黏弹性层状周期板作为轨道交通领域板结构的基本形式,并考虑轨道交通结构振动计算的特点.提出了垂向移动简谐载荷作用下,对边自由对边简支板动力计算的近似理论与解答.首先,引入了板理论的Reissner-Mindlin假设,根据等效截面法确定层状周期板中性轴位置,并结合应力边界条件计算出中性面上横向剪应力;然后,对Reissner-Mindlin假设补充计算条件,以中性面上的横向剪切变形作为板横截面上的整体剪切变形,建立了中性面法线转角与中性面上剪应力的关系;最后,结合平衡方程和应力连续条件,推导了黏弹性层状周期板振动控制方程,提出了考虑横向剪切变形的黏弹性层状周期板近似理论及移动简谐载荷下黏弹性层状周期板振动位移简化Fourier级数形式解.分别与传统方法和有限元计算结果进行了比较,该解在形式和计算上都较为简洁,且精度满足要求,可为黏弹性层状周期板在轨道交通减振领域的设计及推广提供一定理论基础.
1 黏弹性层状周期板近似理论及求解
1.1 基本方程
黏弹性层状周期板沿板厚方向设置周期子结构层,如图1所示.图1中,层A和层B为一个周期单元:层A为弹性层,层高为h,长度l,宽度b;层B为黏弹性层,尺寸同层A.黏弹性层B在提供一定黏弹性的同时也可作为结构承重层,可选择的黏弹性层B的材料有沥青混凝土[31]、环氧沥青混凝土[32]等.
对图1所示的黏弹性周期板做垂向简谐载荷作用下的动力分析,为考虑板内横向剪应力及层间剪切变形,引入Reissner-Mindlin假设,即:
(1)变形前的中性面法线在变形后仍保持为直线,但不一定与中性面垂直;
(2)与面内应力σx,σy,τxy相比,另外3个应力分量σz,τzx,τzy很小,在计算应变时可以忽略不计.
考虑材料为各向同性,黏弹性周期板的基本方程如下:
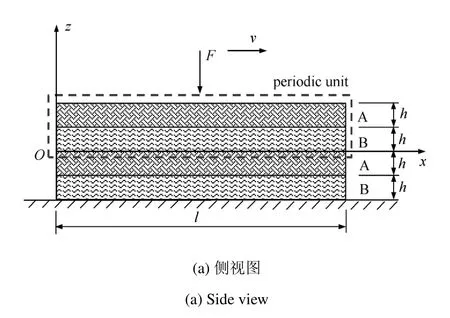
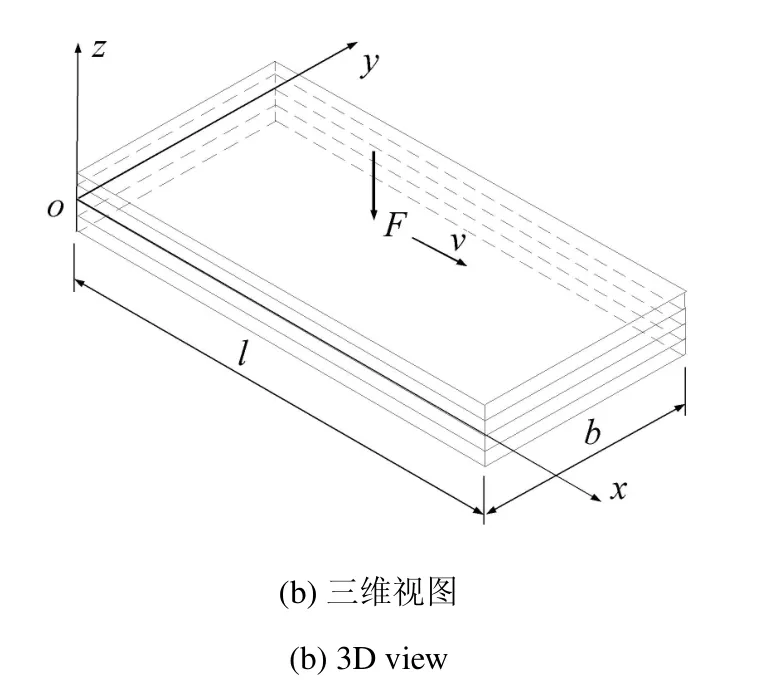
图1 黏弹性层状周期板示意图Fig.1 Viscoelastic layered periodic plate
应力平衡方程(不计体力)
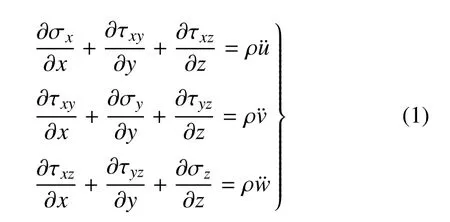
几何方程
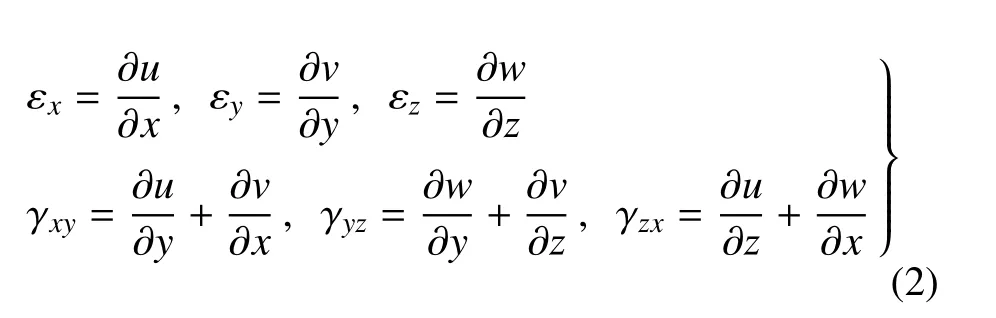
黏弹性层物理方程

弹性层物理方程
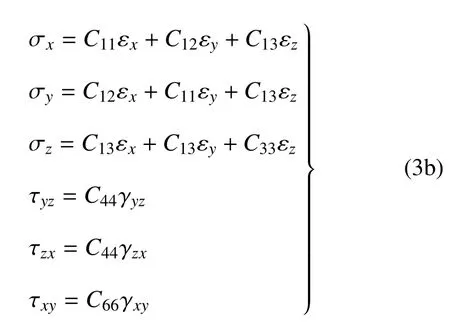
式中,σx,σy,σz,τzy,τzx,τxy为应力;εx,εy,εz,γyz,γzx,γxy为应变;u,v,w分别为x,y,z方向的位移;Y(1)(t)和Y(2)(t)为松弛模量,分别描述应力的偏量部分和球量部分的松弛特性[33];*表示斯蒂尔吉斯卷积;C11,C12,C13,C33,C44,C66为弹性系数.
由假设(2)可知σz=0,代入式(3a)和式(3b)并进行Laplace变换,可得
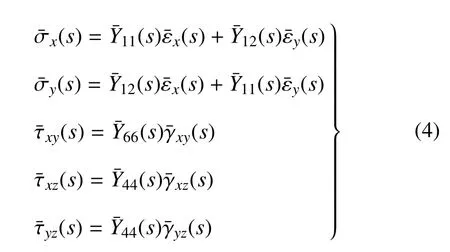
对弹性层A(各向同性材料),有
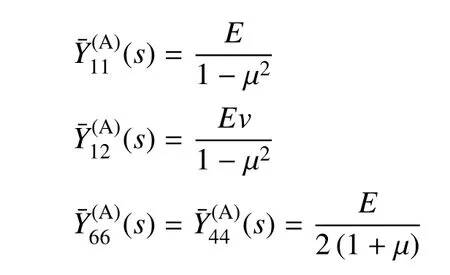
对黏弹性层B,有
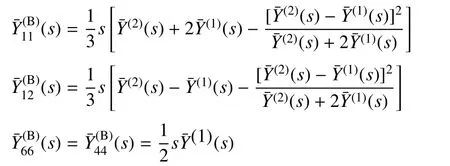
1.2 移动简谐载荷下板振动位移解析求解
计算黏弹性层状周期板中性面的位置,设中性面到中面的距离为z0(如图2所示),则中性面的位置可由下式[34]确定
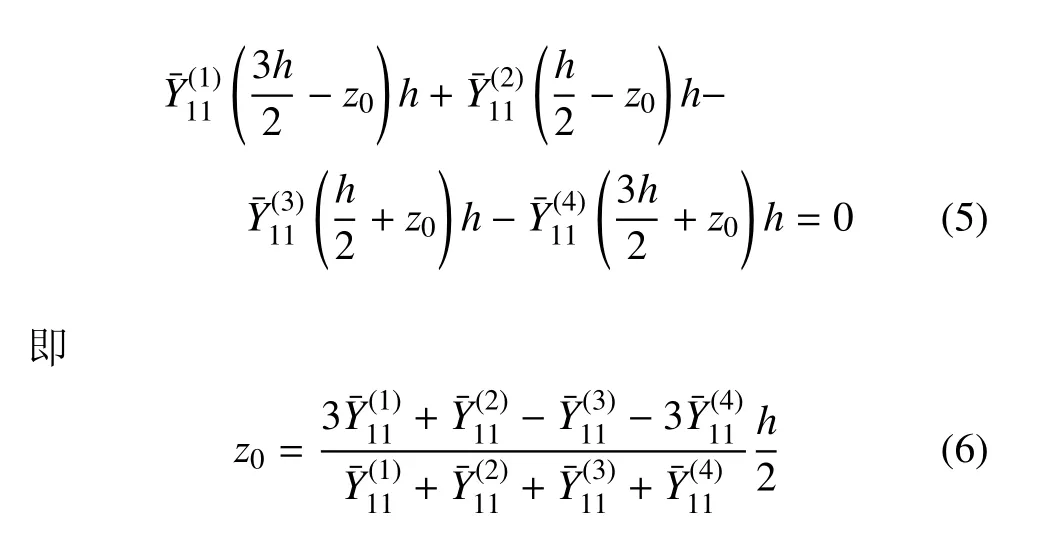
式中上标(1)∼(4)表示板每一层编号.
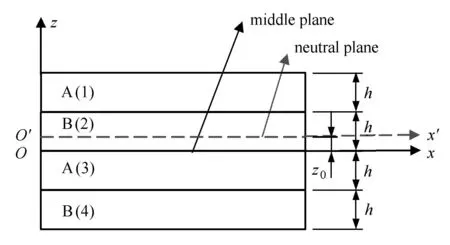
图2 中性面位置示意图Fig.2 Location of the neutral plane
令中性面上z=0,由假设(1)可得板内位移为
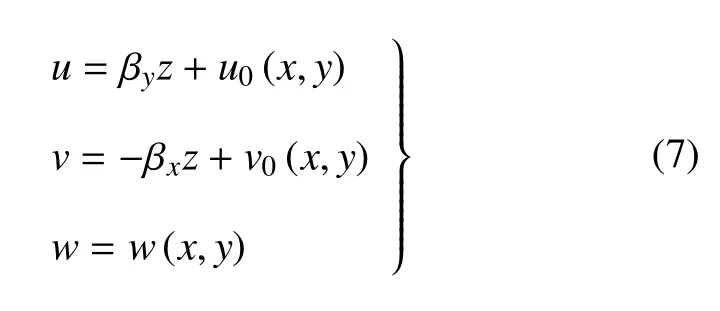
式中,βx和βy分别为中性面法线绕x和y轴的转角,正负号按右螺旋法则确定;u0和v0为中面上的面内位移.
将式(1)和式(7)进行Laplace变换得
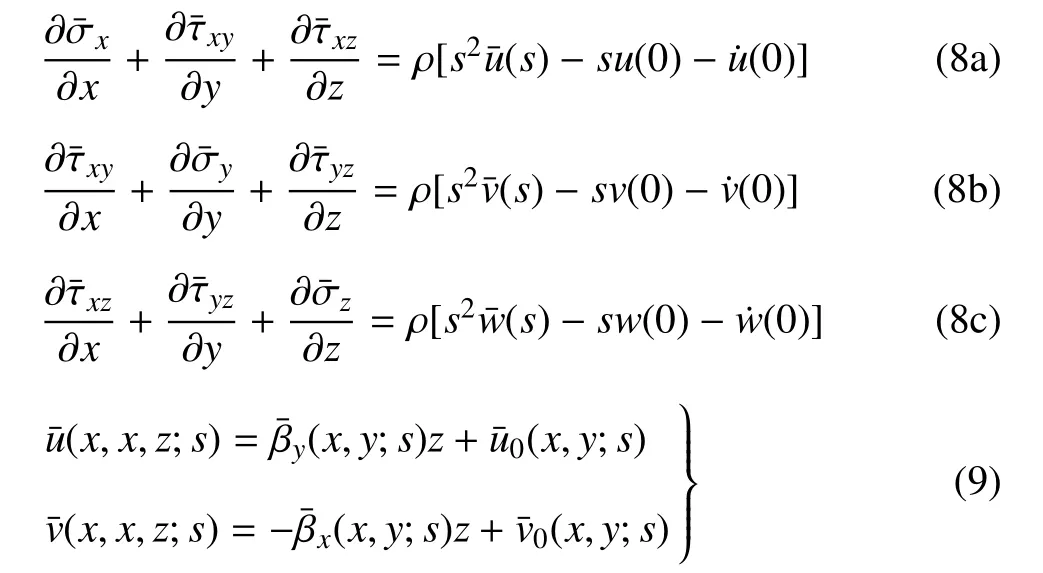
假设初始位移和初始速率为0,将式(4)代入式(8a)和式(8b),并利用式(9)和几何方程式(2),再从0到z积分,考虑到初值定理,可得
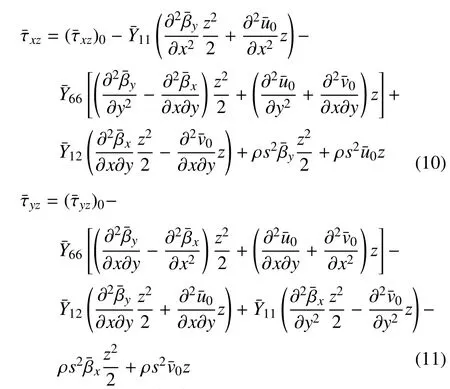
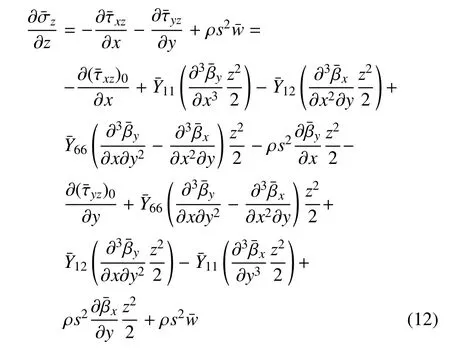
由图2可知,板的上表面为ztop=2h−z0,下表面为zbot=−(2h+z0).将ztop及zbot表达式代入式(10)和式(11)可得

式中,标号(A)和(B)分别代表板一个周期单元内,弹性层A和黏弹性层B的材料参数.
令板上下表面剪应力为0,将式(13)和式(14)代入式(12),并从−z0−2h到2h−z0对z分段积分,得到
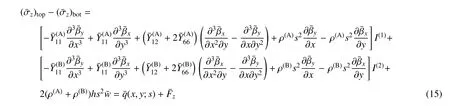
式中
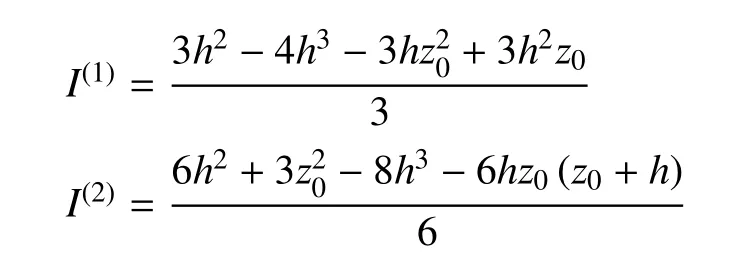
当板上的载荷为沿板中心线匀速移动的单位简谐载荷时
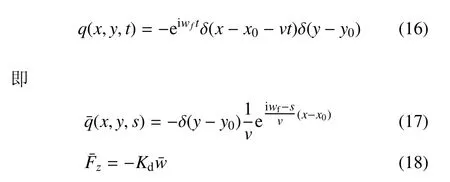
式中,x0和y0为载荷初始位置的坐标,v为载荷的移动速度,wf为载荷的角频率,Kd为板下支承层刚度.
式(15)包含未知量w,βx,βy,想要求解垂向位移w,根据本构关系(3a)和(3b)和变形几何条件(2),对Reissner-Mindlin假设引入补充条件:
(1)以中性面上的横向剪切变形作为板横截面上的整体剪切变形;
(2)变形前的中性面法线在变形后与变形后的中性面法线的夹角等于该处中性面上的剪应变.于是有
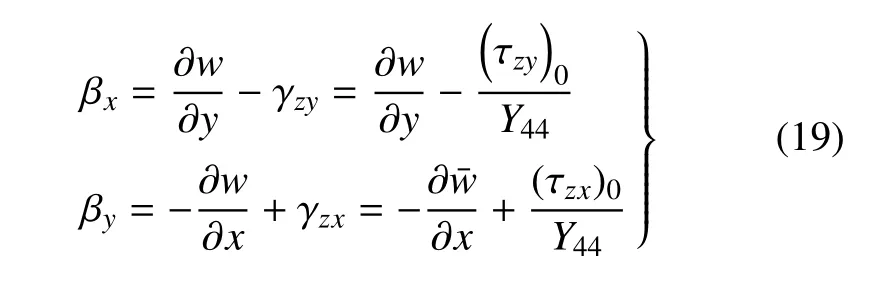
将式(13)和式(14)代入式(19)并进行Laplace变换,得
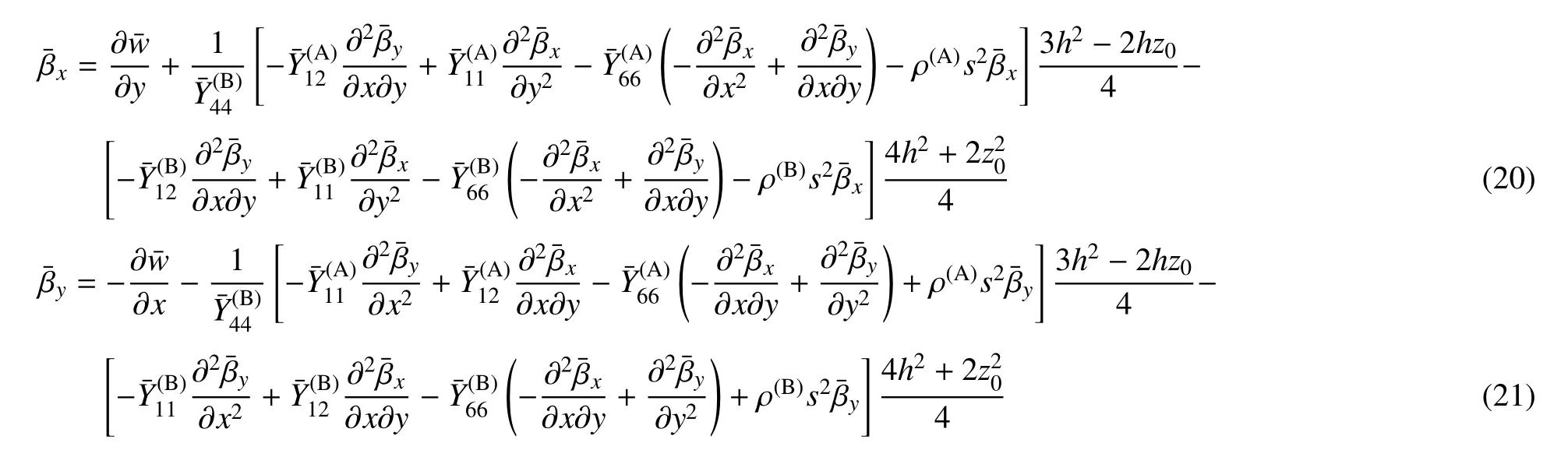
到此,联立式 (15),式 (17),式(18),式 (20)和式(21),并根据边界条件,即可求解单位垂向简谐载荷下层状周期板的振动位移.
设板在x=0和x=l的边界上简支,即
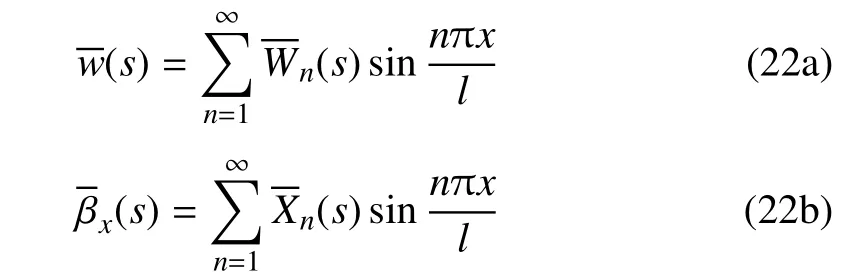
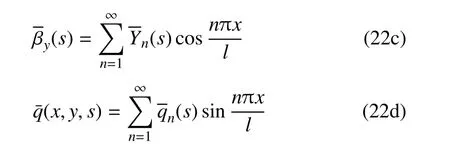
将式(22a)∼式 (22d)代入式(15),式(17),式(18),式(20)和式(21)可得求解级数系数的方程
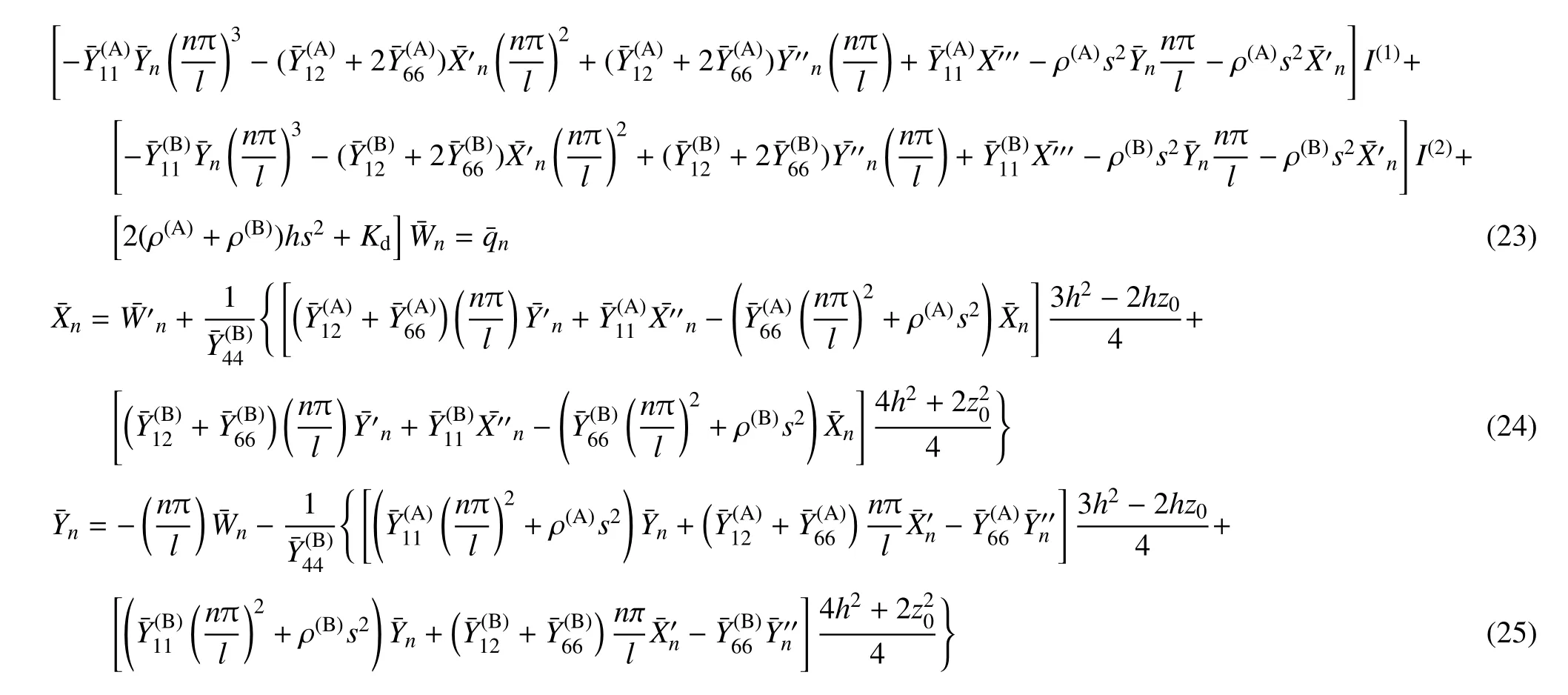

式中,ri为级数系数方程对应齐次方程的特征根;为与ri有关的系数;为待定常数,由y=0,y=b两边的边界条件以及板在载荷作用点两侧的位移、转角、弯矩、扭矩连续和剪力的平衡条件确定.两边自由时,满足以下边界条件
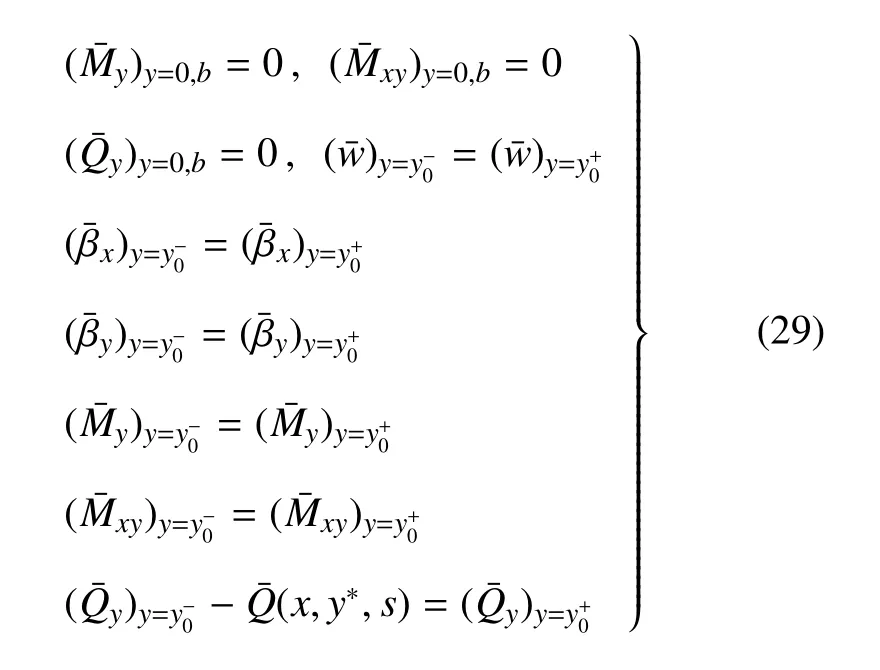
式中,My,Qy,Mxy分别为zoy平面内的弯矩、剪力、扭矩,按传统方法定义.
为了得到时域中板的动力响应,需对Laplace变换域中相应的物理量进行逆变换.由于象函数复杂,且精度要求较高,本文采用Durbin改进后的Laplace逆变换法[35]
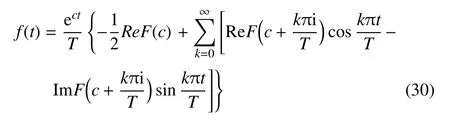
取cT=5,T=20,k=2000.
2 模型验证
采用本文模型计算黏弹性层状周期板的振动位移并与既有计算方法进行比较.计算周期板的几何尺寸如图3所示.由图3,板长度l=4.962m,宽度b=2.55m,厚度4h=0.2m.弹性层选用混凝土,黏弹性层选用黏弹性橡胶材料,相关计算参数如表1所示.
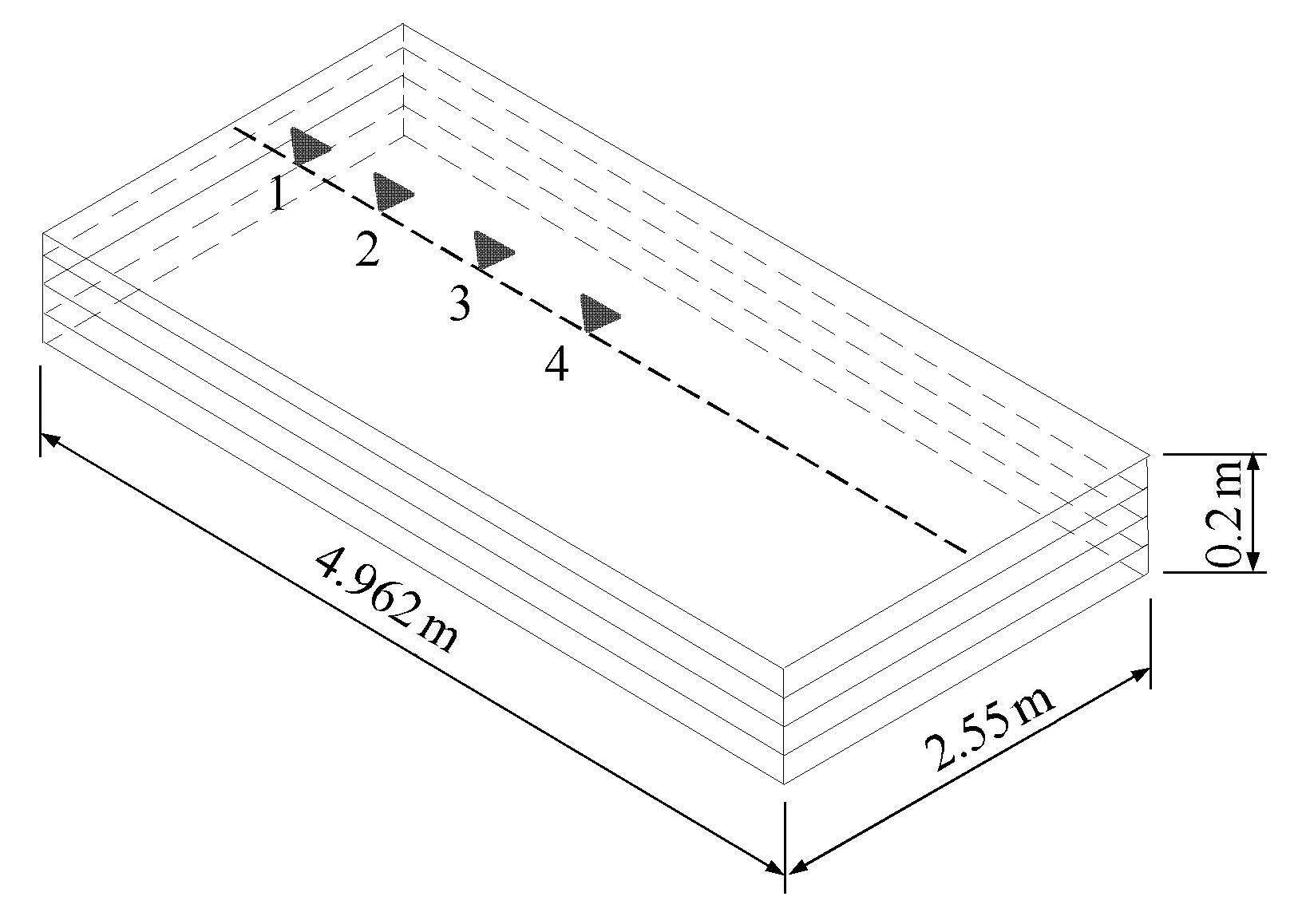
图3 板几何尺寸Fig.3 Geometric size of the plate
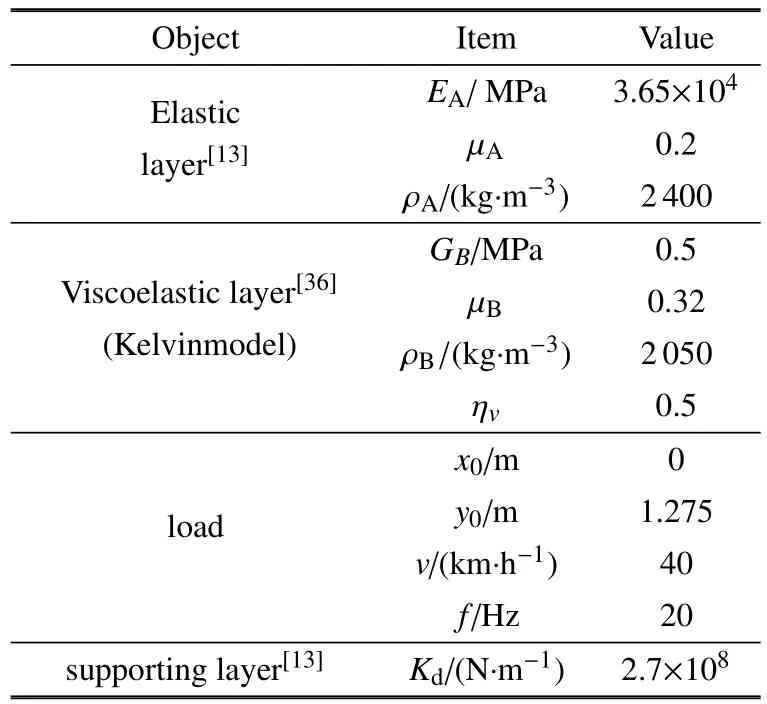
表1 验证模型计算参数Table 1 Parameters of model
分别采用经典层合板模型 (基于 Kirchho ff假设)、本文模型及有限元法计算某时刻板中心线上的垂向位移w,如图4所示.
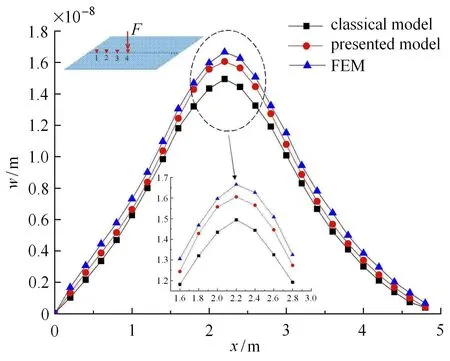
图4 本文模型解答与既有计算方法比较(t=0.2s)Fig.4 Comparison of displacement curves by presented and other solutions(t=0.2s)
经典层合板模型是指将式(19)中略去剪切变形项,即
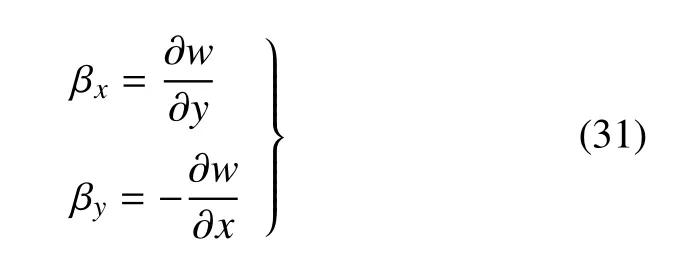
式(31)表示变形前的中性面法线在变形后仍与中面垂直,即经典层合板模型采用的Kirchho ff假设.将式(31)代入式(15)可得只含板振动位移w的控制方程,即
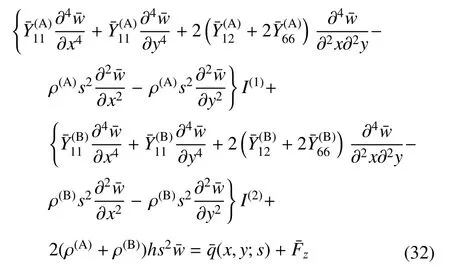
将式(22a)代入式(32),并结合边界条件式(33)即可求得板垂向位移w
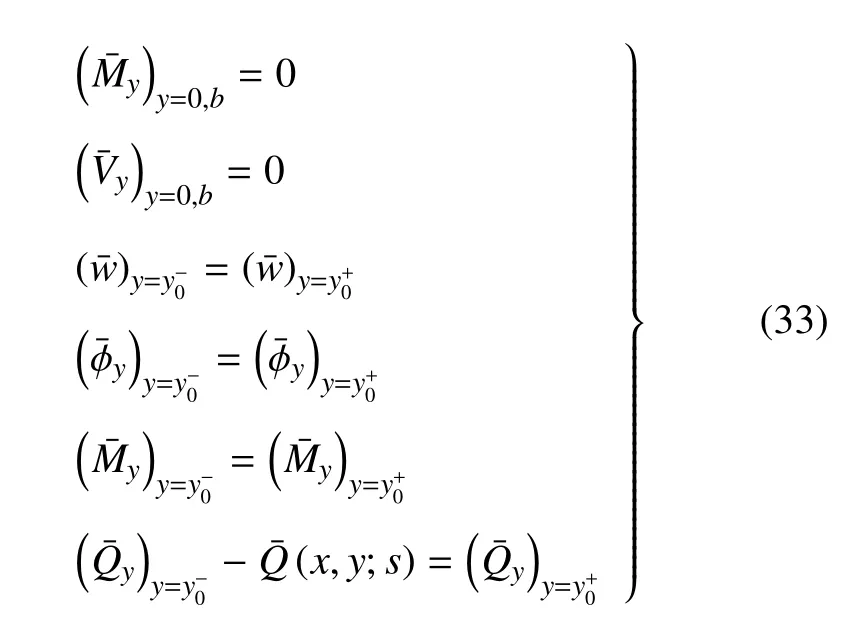
有限元解采用有限元软件ABAQUS通过三维建模得到,选用六面体八节点缩减积分单元(C3D8R)划分实体单元网格,并在载荷区域进行网格加密,单元数为80500.
由图 4可知,本文模型解与有限元解吻合较好,可整体反应出板在载荷作用下的瞬态变形,经典模型解与有限元解有约12%的误差,明显大于本文模型解与有限元解的差值.究其原因,数值解是基于有限元软件计算得到的三维数值结果,单元数量足够多,可以认为该解答的精度最高,与实际情况最接近.经典模型忽略了板内的横向剪切变形,即无法考虑剪变形和挤压变形引起的位移[37],故计算结果小于有限元解.本文模型在经典模型的基础上考虑了板的横向剪切变形,即增加了剪变形引起的位移项,因此比经典模型解更接近于有限元解.但是本文模型仍然对板的内部变形做了约束,人为定义了板内的横向剪应力分布,导致板相较真实情况刚度增大,所以本文模型解仍小于有限元解,但误差在合理范围内.
表2为板上4个测点的振动位移在不同计算方法下的数值.由表2可知,测点1与载荷作用点距离大,振动位移幅值小,且解析解与有限单元解差别较小.测点4比测点1更接近载荷作用点,振动位移幅值大,且振动位移的解析解与有限单元解的差值增大.在本文计算条件下,本文模型与有限元解的最大差值在合理范围内,可以认为计算模型是有效的.
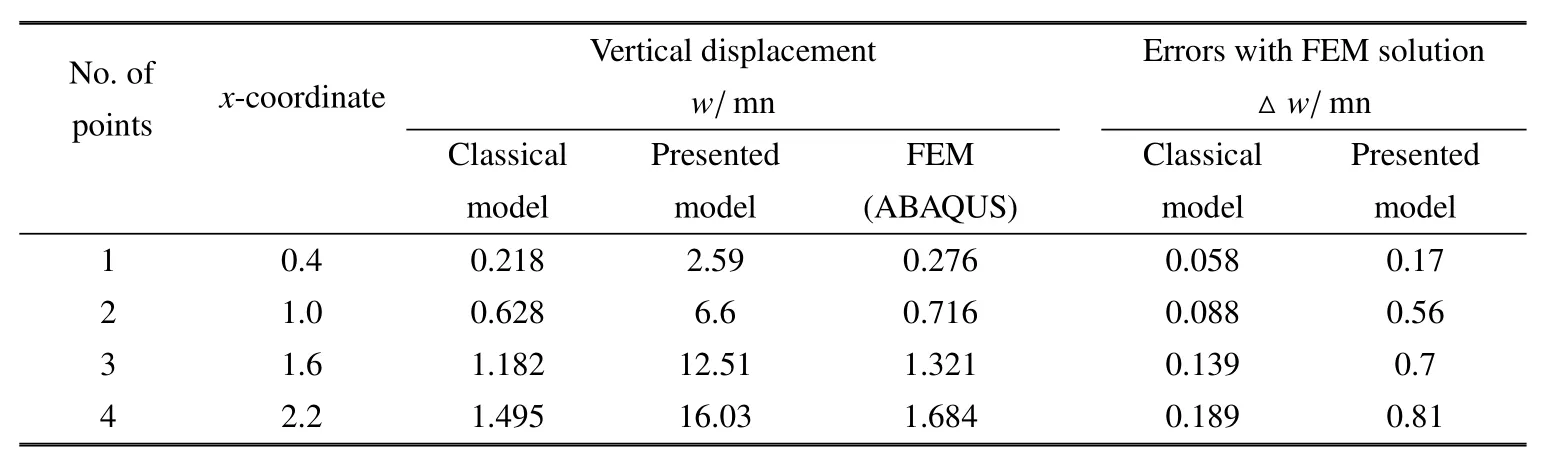
表2 点1∼4垂向位移的解析解与有限单元解比较(y=1.275m)Table 2 Comparison of displacement by analytical and FEM solutions at some points(y=1.275m)
进一步对比不同时刻下板的变形规律,如图5所示.图5为t=0.1s和0.2s时刻下板的整体位移响应,由图可看出,随着计算时间增加,载荷沿着板中心线移动,板位移的峰值也相继发生变化.图5(a)和图5(b)中板位移峰值分别为x=1.1m和x=2.2m,计算结果吻合类似文献[38]和工程实践的认识,可以认为本文所得模型是合理的.
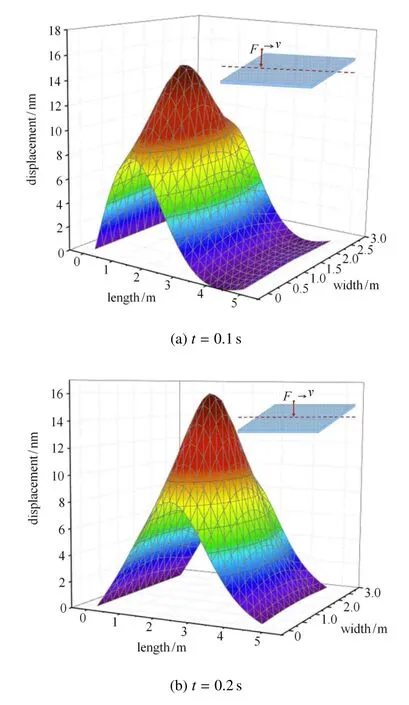
图5 不同时刻下板的振动响应Fig.5 Vibration response of plate at di ff erent time
3 计算结果分析
3.1 导纳特性分析
本文从频域角度出发,以频率响应函数(导纳)为评价指标,研究板的垂向振动特性.图6为板的垂向位移导纳,计算参数见表1.由图6可知,黏弹性层状周期板结构及材料组成多样,振动模态丰富,垂向位移导纳呈现多个峰值.位移导纳在达到第5阶共振频率前,随频率的增大而增大;超过第5阶共振频率后,随着频率的增大而减小.当激励频率在50Hz附近时,板位移导纳达到最大,周期板在共振频率下的垂向位移导纳见表3.
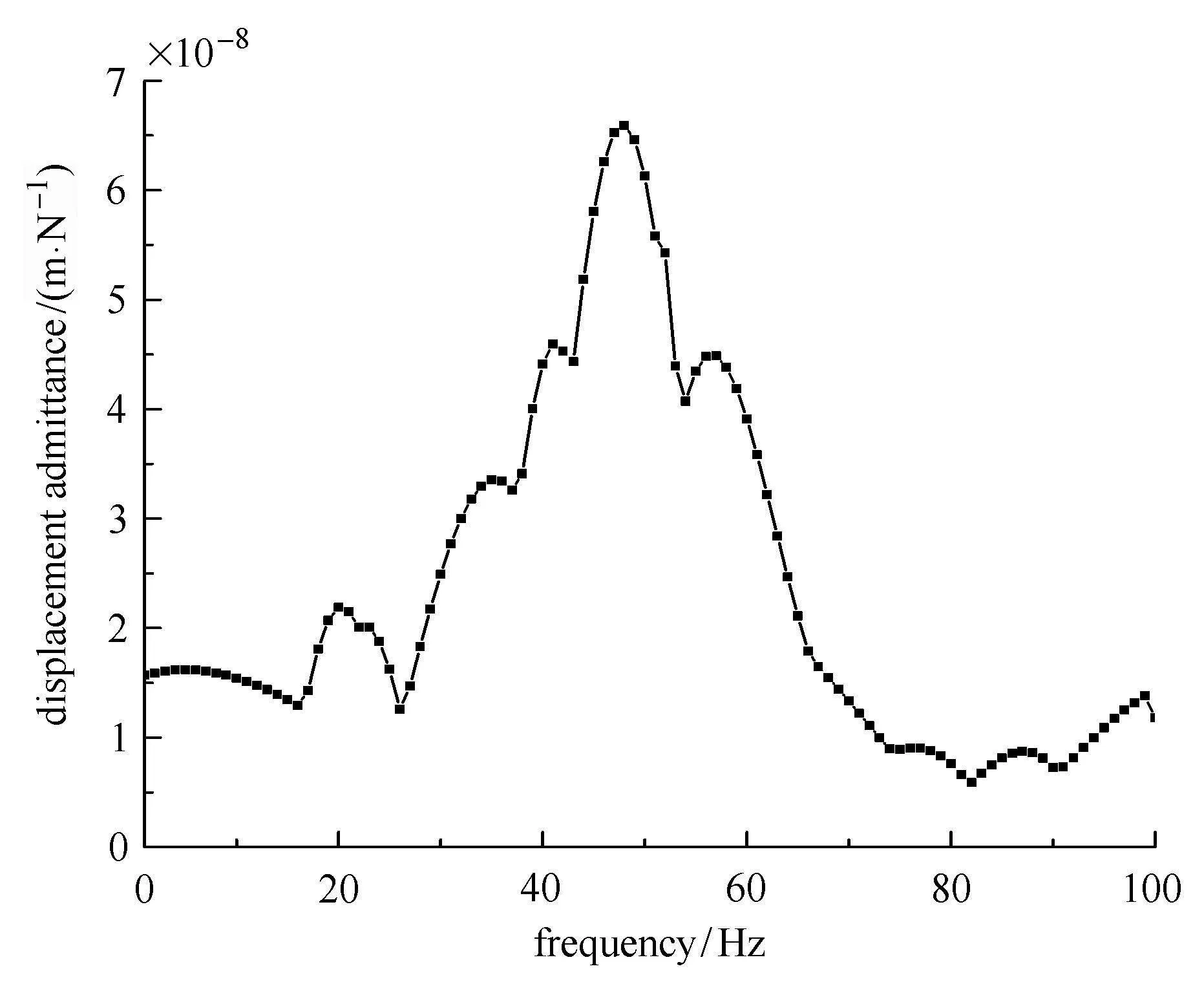
图6 板垂向位移导纳Fig.6 Vertical displacement admittance of plate

表3 板位移导纳峰值Table 3 Vertical displacement admittance peak of plate
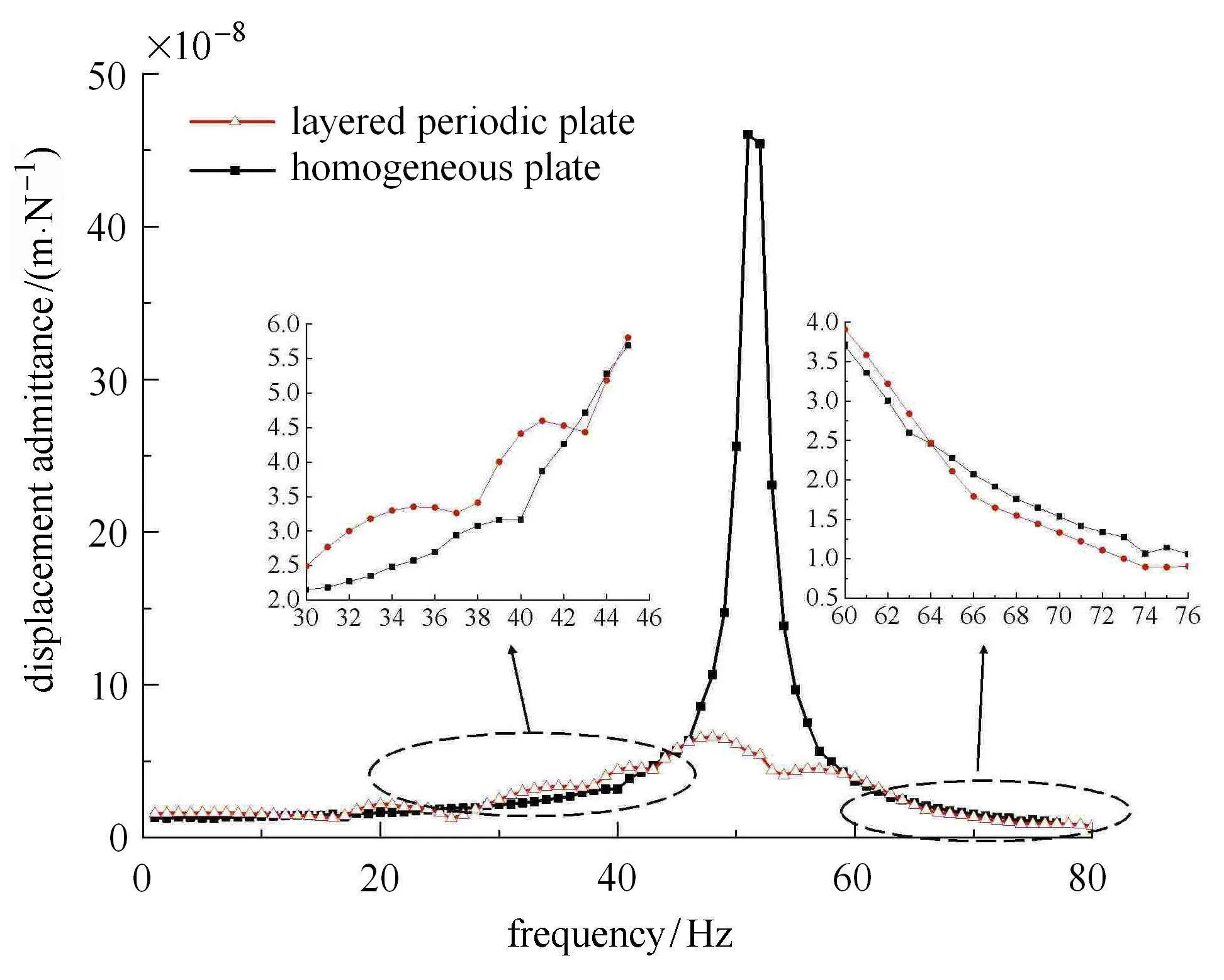
图7 两种板位移导纳的对比Fig.7 Comparison of vertical displacement admittance by di ff erent plates
为衡量黏弹性层状周期板相较于单一材料板的减振能力,图7对比了两种板的垂向位移导纳值,其中,单一材料板的材料参数同黏弹性层状周期板的弹性层,具体数值见表1.由图7可知,单一材料板自振频率成分单一,位移导纳极值为4.6×10−7m/N,对应频率为51Hz;黏弹性层状周期板导纳极大值为6.6×10−8m/N,对应频率为48Hz.由此可见,采用黏弹性层状周期板,可以显著降低单一材料板在自振频率处的振动响应,最大减少量达到3.9×10−7m/N,占整体位移响应的85%,且两种板位移导纳极值对应的自振频率接近.但是,在30∼40Hz范围内,黏弹性层状周期板的振动响应大于单一材料板,最大放大值可达到1.25×10−8m/N,占位移响应的28%;60Hz以上的频段,两种板振动响应相差不大.
3.2 载荷移动速度的影响
取载荷速度分别为40km/h,100km/h,200km/h,300km/h,400km/h,500km/h,600km/h,计算黏弹性层状周期板垂向振动位移的极大值,计算结果如图8所示.由图8可知,在本文计算条件下,随着载荷移动速度的增加,板垂向振动位移增大.载荷速度小于300km/h时,板振动位移增大幅度显著,尤其是100km/h∼200km/h区间,位移增大值达 2.5×10−8m.当载荷速度超过300km/h,板振动位移增大幅度减缓:300km/h∼500km/h区间,位移增大0.84×10−8m,500km/h∼600km/h区间,位移增大 0.08×10−8m.
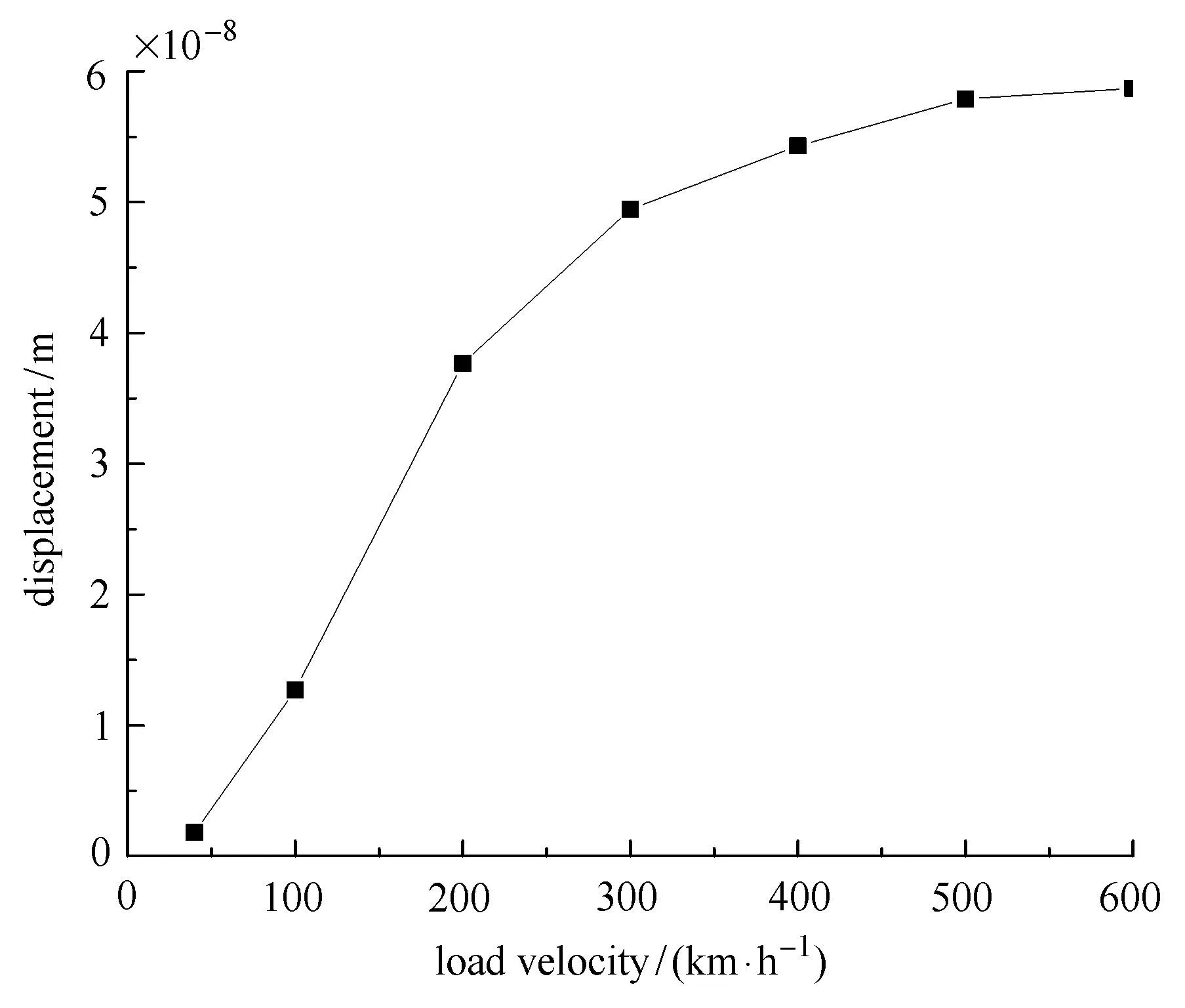
图8 载荷移动速度的影响Fig.8 The in fl uence of load velocity
3.3 材料参数及几何尺寸的影响
探讨黏弹性层材料参数及板几何尺寸对隔振性能的影响,采用力传递率评价板的隔振性能[39],定义为

式中,Fstran是板传给板下基础的力的幅值和,Fstran=|Fz|=Kd|w|;F是外激励的幅值.
图9为稳态振动下,黏弹性层剪切模量GB=10−6GA∼10−2GA时,板力传递率的变化曲线.由图8可看出,黏弹性层剪切模量较小时,结构力传递率较大,达到0.88;增加黏弹性层的剪切模量,结构力传递率先快速减小,从0.88降到了0.22,减小量达75%;之后,当黏弹性层与弹性层剪切模量比值超过10−4后,结构力传递率趋近稳定,呈缓幅增大,从0.22增加到0.26.由此可见,黏弹性层剪切模量存在最佳设计值,可使结构的力传递率达到最小,这给黏弹性层状周期板的材料参数设计提供有益思路.
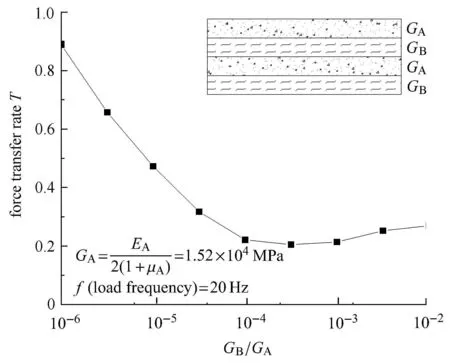
图9 力传递率随着剪切模量的变化曲线Fig.9 Force transfer rate varies with shear modulus
图10为稳态振动下,黏弹性层损耗因子的变化对板力传递率的影响.由图10可知,黏弹性层的阻尼特性对结构振动响应具有一定抑制作用.当结构没有黏性,即损耗因子取0时,力传递率为0.598.之后损耗因子增至0.5,力传递率缓幅减小,但衰减幅度低,力传递率仅降低0.02.究其原因,激励频率较低,为20Hz,黏弹性层的阻尼特性在低频范围内对结构振动响应的影响较小.
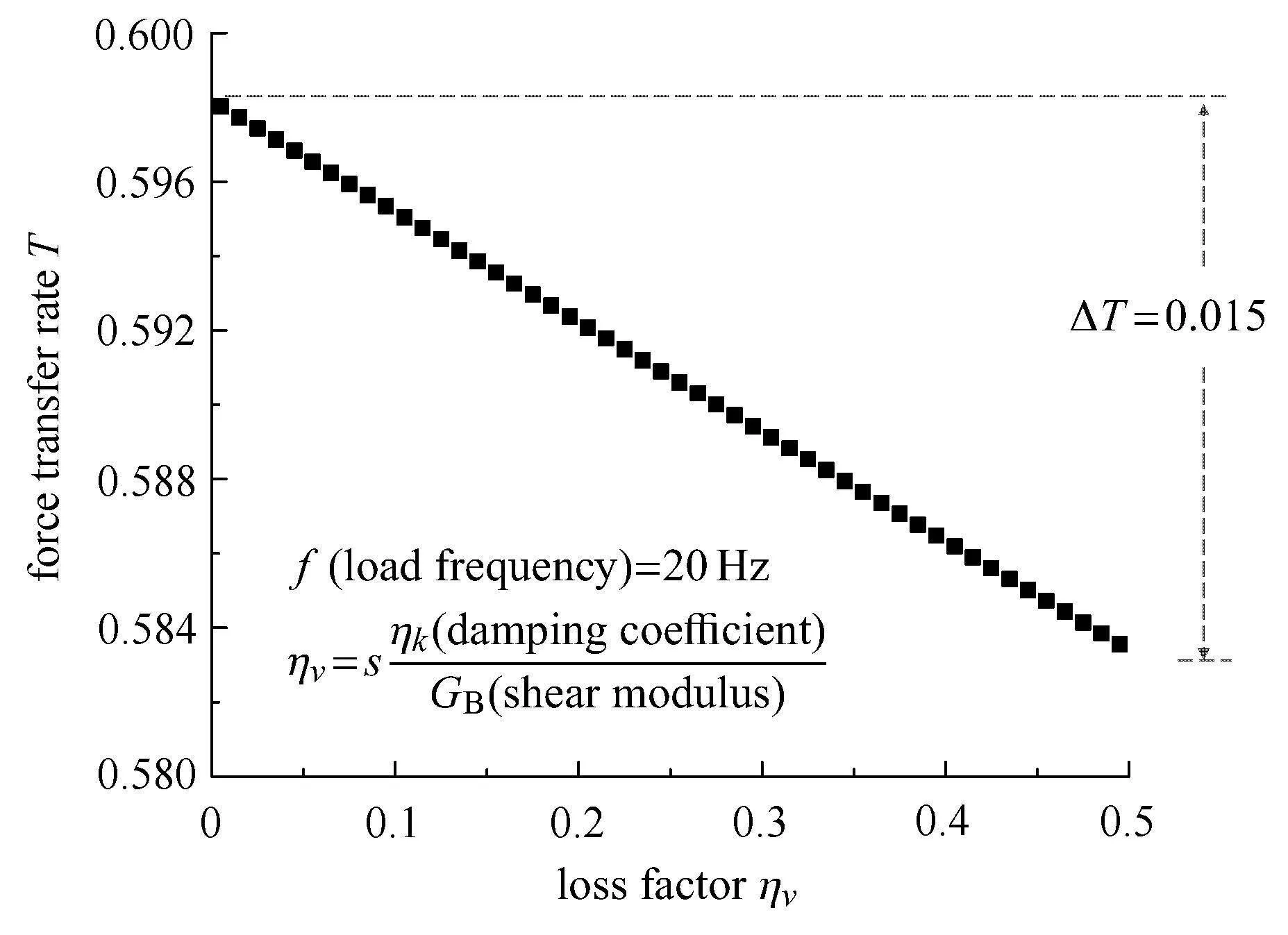
图10 力传递率随损耗因子的变化曲线Fig.10 Force transfer rate varies with loss factor
图11为稳态振动下,板的长度变化对隔振性能的影响曲线,评价指标取单位长度力传递率,即力传递率T与板长l的商.由图11可知,随着板的长度增加,结构参振质量增大,力传递率减小,隔振性能增加.当板的长度由5m增加至11m时,单位长度力传递率衰减显著,从0.197降到了0.077,衰减度达76%;之后继续增加板长,结构单位长度力传递率平缓降低,从0.077减小至0.039.对于轨道交通领域的板结构,板的长度受限于施工条件等因素,因此可考虑适当增加板长,以提高结构的隔振性能.
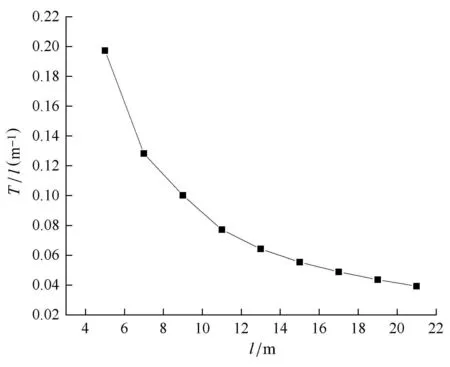
图11 板长对隔振性能的影响Fig.11 Vibration isolation performance varies with length
4 结论
针对单位移动简谐载荷下,对边简支对边自由黏弹性层状周期板动力计算问题,本文提出了相应的近似理论与解析解答.模型计算形式简洁,计算效率高,可以考虑板内横向剪应力的影响.通过与经典层合板模型和三维有限元计算结果的比较,验证了解答的有效性.本文模型可为黏弹性层状周期板在轨道交通减振领域的设计及推广提供一定理论基础.
利用本文计算方法研究了某黏弹性层状周期板在频域内的动力响应,得到如下结论:
(1)采用黏弹性层状周期板可以显著降低单一材料板在自振频率处的振动响应,但会引起局部低频频段的振动放大;
(2)本文计算条件下,板的垂向位移随着载荷速度的增加而增大,超过300km/h后,载荷速度对板振动响应的影响减弱;
(3)黏弹性层剪切模量存在最佳设计值,可使结构的隔振性能最佳;
(4)黏弹性层的阻尼特性在低频范围内对结构振动的影响较小;
(5)可在满足工程实际的情况下适当增加板长,以提高结构的隔振性能.
1 Kushwaha MS,Halevi P,Mart´ınez G,et al.Theory of acoustic band structure of periodic elastic composites.Phys Rev B Condens Matter,1994,49(4):2313-2322
2 Brillouin L.Wave Propagation in Periodic Structures:Electric Filters and Crystal Lattics.Dover Publications,Inc,2003
3 温激鸿,王刚,郁殿龙等.声子晶体振动带隙及减振特性研究.中国科学,2007,37(9):1126-1139(Wen Jihong,Wang Gang,Yu Dianlong,et al.Vibration attenuation and band gap characteristics of phononic crystals.Scientia Sinica Technologica,2007,37(9):1126-1139(in Chinese))
4 黄毓.弹性波带隙材料/结构优化设计.[博士论文].大连:大连理工大学,2014(Huang Yu.Optimization design of elastic wave bandgap material/Structures.[PhD Thesis].Dalian:Dalian University of Technology,2014(in Chinese))
5 朱晓辉,李隆球,张广玉等.基于层状周期性结构的声波调控技术研究.机械工程学报,2017,53(6):10-15(Zhu Xiaohui,Li Longqiu,Zhang Guangyu,et al.Investigation of acoustic manipulation by layered periodic composites.Journal of Mechanical Engineering,2017,53(6):10-15(in Chinese))
6 Shi Z,Huang J.Feasibility of reducing three-dimensional wave energy by introducing periodic foundations.Soil Dynamics&Earthquake Engineering,2013,50(1):204-212
7 Yan Y,Laskar A,Cheng Z,et al.Seismic isolation of two dimensional periodic foundations.Journal of Applied Physics,2014,116(4):1-12
8 Huang J,Shi Z,Huang W,et al.A periodic foundation with rotational oscillators for extremely low-frequency seismic isolation:analysis and experimental veri fi cation.Smart Material Structures,2017,26
9 程志宝,石志飞,向宏军.层状周期结构动力衰减域特性研究.振动与冲击,2013,32(9):178-182(Cheng Zhibao,Shi Zhifei,Xang Hongjun.Vibration attenuation zones of a laminated periodic structure.Journal of Vibration and Shock,2013,32(9):178-182(in Chinese))
10 黄建坤.周期性排桩和波屏障在土木工程减振中的应用研究.[博士论文].北京:北京交通大学,2014(Huang Jiankun.Application of periodic pile barriers and wave barriers to reduce vibrations in civil engineering.[PhD Thesis].Beijing:Beijing Jiaotong University,2014(in Chinese))
11 程志宝.周期性结构及周期性隔震基础.[博士论文].北京:北京交通大学,2014(Cheng Zhibao.Periodic structures and periodic seismic isolation foundations.[PhD Thesis].Beijing:Beijing Jiaotong University,2014(in Chinese))
12 Cheng ZB,Yan YQ,Menq FY,et al.3D periodic foundation-based structural vibration isolation.Proceedings of the World Congress on Engineering&Computer Scie,2013
13 翟婉明.车辆--轨道耦合动力学.北京:科学出版社,2007(Zhai Wanming.Vehicle-track Coupling Dynamics.Beijing:Science Press,2007(in Chinese))
14 Knothe K.Gleisdynamik.Berlin:Ernst&Sohn,2001
15 叶敏,吕敬,丁千等.复合材料层合板1:1参数共振的分岔研究.力学学报,2004,36(1):64-71(Ye Min,LJing,Ding Qian,et al.The bifurcation analysis of the laminated composite plate with 1:1 parametrically resonance.Chinese Journal of Theoretical and Applied Mechanics,2004,36(1):64-71(in Chinese))
16 王晓丹.满足层间连续条件的层合板理论及其准确和高效的板单元.[博士论文].天津:天津大学,2015(Wang Xiaodan.Laminated composite plate theories accounting for interlaminar continuity and its accurate,efficient plate elements.[PhD Thesis].Tianjin:Tianjin University,2015(in Chinese))
17 Duan TC,Li LX.The uni fi ed solution for a beam of rectangular cross-section with di ff erent higher-order shear deformation models.Latin American Journal of Solids and Structures,2016,13:1716-1737
18 段铁城,李录贤.厚板的高阶剪切变形理论研究.力学学报,2016,48(5):1096-1113(Duan Tiecheng,Li Luxian.Study on higherorder shear deformation theories of thick-plate.Chinese Journal of Theoretical and Applied Mechanics,2016,48(5):1096-1113(in Chinese))
19 李念,陈普会.复合材料层合板低速冲击损伤分析的连续介质损伤力学模型.力学学报,2015,47(3):458-470(Li Nian,Chen Puhui.Continuum damage mechanics model for low-velocity impact damage analysis of composite laminates.Chinese Journal of Theoretical and Applied Mechanics,2015,47(3):458-470(in Chinese))
20 徐巍,王立峰,蒋经农.基于应变梯度中厚板单元的石墨烯振动研究.力学学报,2015,47(5):751-761(Xu Wei,Wang Lifeng,Jiang Jingnong.Finite element analysis of strain gradient middle thick plate model on the vibration of graphene sheets.Chinese Journal of Theoretical and Applied Mechanics,2015,47(5):751-761(in Chinese))
21 陈建霖,励争,储鹏程.大开口复合材料层合板强度破坏研究.力学学报,2016,48(6):1326-1333(Chen Jianlin Li Zheng,Chu Pengcheng.Strength analysis of fi ber reinforced composite laminates with big cutouts.Chinese Journal of Theoretical and Applied Mechanics,2016,48(6):1326-1333(in Chinese))
22 Chen WQ,Ding HJ.On free vibration of a functionally graded piezoelectric rectangular plate.Acta Mechanica,2002,153(3-4):207-216
24 Yang M,Qiao P.Higher-order impact modeling of sandwich structures with fl exible core.International Journal of Solids&Structures,2005,42(20):5460-5490
25 C¸alim FF.Free and forced vibrations of non-uniform composite beams.Composite Structures,2009,88(3):413-423
26 Ganapathi M,Kalyani A,Mondal B,et al.Free vibration analysis of simply supported composite laminated panels.Composite Structures,2009,90(1):100-103
27 李尧臣,亓峰,仲政.功能梯度矩形板的近似理论与解析解.力学学报,2010,42(4):670-681(Li Yaochen,Qi Feng,Zhong Zheng.Approximate theory and analytical solution for graded piezoelectric rectangular plates.Chinese Journal of Theoretical and Applied Mechanics,2010,42(4):670-681(in Chinese))
28 李尧臣,聂国隽,杨昌锦.面内功能梯度矩形板的近似理论与解答.力学学报,2013,45(4):560-567(Li Yaochen,Nie Guojun,Yang Changjin.Approximate theory and analytical solution for rectangular plates with in-plane sti ff ness gradient.Chinese Journal of Theoretical and Applied Mechanics,2013,45(4):560-567(in Chinese))
29 Thai HT,Nguyen TK,Vo TP,et al.Analysis of functionally graded sandwich plates using a new fi rst-order shear deformation theory.European Journal of Mechanics-A/Solids,2014,45(2):211-225
30 Pandey S,Pradyumna S.Free vibration of functionally graded sandwich plates in thermal environment using a layerwise theory.European Journal of Mechanics-A/Solids,2015,51:55-66
31 方明镜.高速铁路沥青混凝土轨下基础结构行为与材料设计.[博士论文].成都:西南交通大学,2012(Fang MingJing.Structural behavior and mix design for asphalt concrete substructures in highspeed rail.[PhD Thesis].Chengdu:Southwest Jiaotong University,2012(in Chinese))
32 钱振东,刘阳,刘昕依.高速铁路环氧沥青混凝土基础结构动力响应及设计.东南大学学报(自然科学版),2017,47(1):118-123(Qian Zhendong,Liu Yang,Liu Xinyi.Dynamic response and design of epoxy asphalt concrete substructure for high-speed railway.Journal of Southeast University(Natural Science Edition),2017,47(1):118-123(in Chinese))
33 郭大智,任瑞波.层状黏弹性体系力学.哈尔滨:哈尔滨工业大学出版社,2001(Guo Dazhi,Ren Ruibo.Mechanics of Layered Viscoelastic Systems.Harbin:Harbin Engineering University Press,2001(in Chinese))
34 孙训方,方孝淑,关来泰.材料力学(第五版).北京:高等教育出版社,2009(Sun Xunfang,Fang Xiaoshu,Guan Laitai.al.Mechanics of Materials(5th Edn).Beijing:Higher Education Press,2009(in Chinese))
35 Durbin F.Numerical inversion of laplace transforms:An efficient improvement to dubner and abate’s method.Computer Journal,2013,17(4):371-376
36 杨坤,梅志远,李华东.黏弹性复合材料夹芯板稳态响应分析.振动与冲击,2013,32(7):88-92(Yang Kun,Mei Zhiyuan,Li Huadong.Steady response analysis for a composite sandwich plate with viscoelastic core layer based on Kelvin model.Journal of Vibration and Shock,2013,32(7):88-92(in Chinese))
37 曹志远. 板壳振动理论.北京:中国铁道出版社,1989(Cao Zhiyuan.Vibration Theory of Plates and Shells.Beijing:China Railway Publishing House,1988(in Chinese))
38 王春玲,黄必成,曹彩芹.移动载荷下弹性半空间地基上矩形薄板的动力响应解析研究.土木工程学报,2016,49(1):116-121(Wang Chunling,Huang Bicheng,Cao Caiqin.Analytical study on dynamic response of rectangular thin plate on an elsticc half-space under moving loads.China Civil Engineering Journal,2016,49(1):116-121(in Chinese))
39 杨新文,杨建近.MTMDs对浮置板轨道结构隔振性能的影响分析.铁道学报,2015(4):87-93(Yang Xinwen,Yang Jianjin.E ff ect of MTMDS on the vibration isolation of fl oating slab track.Journal of The China Railway Society,2015(4):87-93(in Chinese))
APPROXIMATE THEORY AND ANALYTICAL SOLUTION FOR DYNAMIC CALCULATION OF VISCOELASTIC LAYERED PERIODIC PLATE
Xu Sihui*,1)Wang Binglong*Zhou Shunhua*Yang Xinwen*Li Yaochen†
*(Key Laboratory of Road and Traffic Engineering of the Ministry of Education,Tongji University,Shanghai201804,China)
†(School of Aerospace Engineering and Applied Mechanics,Tongji University,Shanghai200092,China)
Rail transit loading and viscoelastic of material are mostly ignored in the previous dynamic calculations of the periodic vibration isolation structures.Approximate theory and analytical solution for viscoelastic layered periodic plate subjected to vertical moving harmonic loading is established,and the viscoelastic of material and the transverse shear deformation are considered.In this theory,Reissner-Mindlin assumption and additional equation of shear deformation are introduced,and the relation between the normal rotation and the shear stress of neutral plane is obtained on the assumption that the transverse shear deformation of the plate’s neutral plane is the overall shear deformation of the cross section.Vibrationgoverningequationofviscoelasticlayeredperiodicplateisproposedaccordingtoequilibriumequations and stress continuity conditions,and vertical displacement in Fourier series is derived as well.The model is validated by the good agreement with solution of the classical laminate model and the fi nite element method(FEM).The results show that:(1)Vibration response at the natural frequency of plate can be signi fi cantly reduced by substituting viscoelastic layered periodic plate for homogeneous one,but vibration ampli fi cation in local low frequency band is aroused as well.(2)The vertical displacement of the plate increases with the increment of the loading velocity,and increase trend slows down once velocity above 300km/h.(3)Shear modulus of viscoelastic layer can be designed to achieve the optimal vibration isolation characteristic.(4)Vibration response is not susceptible to damping characteristic in low frequency band.(5)It’s appropriate to increase the plate length,within the engineering requirement,to improve the vibration isolation performance.
periodic structure,rail transit loading,Reissner-Mindlin assumption,analytical solution,vibration response
O328
A doi:10.6052/0459-1879-17-248
2017–07–07 收稿,2017–09–13 录用,2017–09–15 网络版发表.
1)徐司慧,博士研究生,主要研究方向:轨道结构减振.E-mail:xsyh1234@163.com
徐司慧,王炳龙,周顺华,杨新文,李尧臣.黏弹性层状周期板动力计算的近似理论与解答.力学学报,2017,49(6):1348-1359
Xu Sihui,Wang Binglong,Zhou Shunhua,Yang Xinwen,Li Yaochen.Approximate theory and analytical solution for dynamic calculation of viscoelastic layered periodic plate.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1348-1359

