轻敲模式下原子力显微镜的能量耗散1)

魏 征 孙 岩 王再冉 王克俭 许向红

*(北京化工大学机电工程学院，北京100029)

†(中国科学院力学研究所非线性力学国家重点实验室，北京100190)

固体力学

轻敲模式下原子力显微镜的能量耗散1)

魏 征*,2)孙 岩*王再冉*王克俭*许向红†

*(北京化工大学机电工程学院，北京100029)

†(中国科学院力学研究所非线性力学国家重点实验室，北京100190)

原子力显微镜有多种成像模式，其中轻敲模式是最为常用的扫描方式.轻敲模式能获取样品表面形貌的高度信息和相位信息，其中相位信息具有更多的价值，如能反映样品的表面能、弹性、亲疏水性等.依据振动力学理论，相位与振动系统的能量耗散有关.探针样品间的能量耗散对于理解轻敲模式下原子力显微镜的成像机理至关重要，样品特性和测量环境会影响能量耗散.本文在不考虑毛细力影响下，基于JKR接触模型，给出了探针样品相互作用下的加卸载曲线，结合原子力显微镜力曲线实验，给出了探针--样品分离失稳点的位置，从而计算一个完整接触分离过程的能量耗散，进而讨论考虑表面粗糙度对能量耗散的影响.在轻敲模式下考虑毛细力影响，通过特征时间对比，证明挤出效应是液桥生成的主导因素，在等容条件下，用数值方法计算了不同相对湿度对能量耗散的影响.通过一维振子模型，简要说明原子力显微镜相位像与样品表面能、杨氏模量、表面粗糙度、相对湿度之间的关系.分析表明，表面粗糙度和环境湿度均会引起相位的变化，进而认为它们是引起赝像的因素.

原子力显微镜，相位像，黏附，液桥，能量耗散，毛细力

引言

1986年诺贝尔物理学奖授予了电子显微镜和扫描隧道显微镜(scanning tunneling microscope,STM)的发明者.随后一系列的扫描探针显微镜(scanning probe microscope,SPM)面世，这其中就包括原子力显微镜(atomicforcemicroscope,AFM)[1].不同于STM，AFM对扫描样品没有导电的要求，扩大了扫描样品范围，更本质的区别是相对于 STM测量的隧道电流，AFM测量的是探针与样品间的作用力，因此在本源上 AFM比 STM更具有力学 (机械)本质[2].AFM的核心力学传感部件是一根微悬臂梁，在接触式扫描中，通过微悬臂梁的弯曲或扭转变形而得到样品的表面形貌和力学性质(模量、黏性、摩擦等).在非接触模式中(包括轻敲模式)，主要通过微悬臂梁的振幅、相位和频移来反映样品的表面形貌和力学性质[3-4].接触式和轻敲式是AFM的两种最主要形貌成像方式，由于轻敲模式采用的是探针与样品间歇式接触方式，因此这种扫描方式对样品(特别是软物质，如生物组织)的损伤最小.另外通过微悬臂梁的相位变化能提供更多的样品信息，因此轻敲式扫描为最常用的扫描方式.

尽管AFM技术取得了巨大的进步，但其仍然存在很严重的缺陷，即使对于非常熟练的操作者，发现扫描形貌中的干扰因素和赝像都是一件很困难的事情[5-6].赝像产生的原因很多，依据噪声来源，可分为探针因素[5]、扫描器因素[7]、样品因素以及探针与样品相互作用因素[8-10].

尽管赝像问题非常普遍，但近二十年来仅有有限的文献论述了AFM的赝像问题.关于探针与样品之间作用力引起赝像的论述更少[10].在AFM的测量中，若要解释其成像机理，理解针尖和样品之间的黏附力是必不可少的.不得不强调的是，作为一种探针技术，对针尖样品间作用力的准确控制是获得高分辨率形貌的最为重要的因素.不同的样品表面和探针间距会引起不同的作用力，但针尖与样品之间的黏附力在本质上都是电磁作用.针尖与样品之间的黏附力主要由毛细力、静电力、短程斥力、范德华力等构成[11-16].毛细力会掩盖其他作用力，如在有毛细力存在的情况下，范德华力会降1∼2个量级[17].

生物、有机材料或无机材料，由于其亲疏水特性的不同，在不同湿度下，往往会带来扫描图像中高度、相位的差别[12].这些差别都是由于在扫描过程中液桥的生成而非范德华力的作用.因此，在大气环境中，湿度影响液桥的生成、破碎，进而影响毛细力，研究湿度对AFM形貌测量的影响，从而合理地控制毛细力，是避免产生赝像获得高分辨率图像的关键所在.到目前为止，关于湿度对AFM扫描图像的影响的研究还是零星地分布于各文献中[6-7]，没有较系统的研究，甚至还没有明确提出湿度会引起赝像的观点.

AFM轻敲模式下所得相位图比高度形貌图更能反映样品的材料特性，如黏附、弹性以及黏弹性等，相位图反映的是AFM微悬臂梁响应与压电管激振之间的相差[12].按照Cleveland等的观点，相位差与系统的能量耗散有关，能量耗散存在于探针与样品的机械接触中[18].耗散反映了被测材料的黏弹性[19]，利用该特性可以分辨不同种类物质在整个材料中的分布.但不同的作用力使得耗散能不同，从而使相位图像产生变化.

探针与样品间的接触能量耗散是引起轻敲模式下相位变化的主要因素，本文拟将作者多年来对此种接触下各种因素引起的能量耗散进行分析、讨论，以期对成像机理和赝像有更一步的认识.

1 黏附接触对能量耗散的贡献

对于微纳尺度下的接触，在理想情况下，分离两个接触表面所需要的功等于两个表面相接触时所获取的功.但在实际情况下，即使表面力的作用和接触物体的弹性变形是可逆的，将两个表面分离所需要的功仍大于表面相接触时黏着力所做的功，即接触与分离过程是不可逆的，存在能量耗散.这种现象称为黏着接触滞后[20].另外，黏着接触滞后还有一个表现，就是在接触分离过程中，其加载与卸载的路径不同，即卸载具有滞后性，这也是称之为接触滞后的原因，这种滞后在实际界面现象中非常常见.

从能量的观点和加卸载路径的观点分析黏着接触滞后，是处理这类问题的两个基本方法.图1为AFM典型力曲线.当探针从远处向样品接近时，针尖与样品间的作用力很弱，微悬臂梁探针端挠度为0，这一阶段为图中线段ab所示.当探针接近样品一定位置时，探针样品间吸引力越来越大，探针加速撞向样品，此现象为接触突跳(jump in)，为图中c点，为接触分离过程中的第一次失稳过程.探针继续向样品方向移动，探针样品间的作用力变为斥力，微悬臂梁向上弯曲，此过程为cd段.此后探针撤离样品，探针样品的斥力逐渐减小，当微悬臂梁的扰度为零时，继续向上抬离探针，由于探针样品间黏附力的存在，探针样品没有发生分离，这时悬臂梁向下弯曲，探针样品的吸引力随探针向上移动一直增加，如图de段所示.最后当黏附力不足对抗弯曲梁中的弹性力时，发生突跳分离(jump out)，此为接触分离过程中的第二次失稳.下面将介绍第二次失稳发生的条件.

图1 典型AFM力曲线Fig.1 A typical AFM force curve

将AFM探针样品作用简化为球、弹簧、样品系统，如图2所示.其接触分离过程中存在两个失稳点，即在针尖趋近基底的过程中，针尖与基底的相互吸引力会越来越强，最终吸引力的梯度大于AFM微悬臂刚度时，进入突跳接触失稳(jump in)，当针尖脱离基底时，在某个位置上，同样存在黏着力的梯度大于微悬臂的刚度，进入分离失稳(jump out)，图1给出了这两个失稳的位置.因此，这两个失稳都是发生在探针样品间作用力梯度等于或即将大于微悬臂梁刚度的位置，这种失稳属于“力学不稳定性”[20].显然这类力学失稳，会引起加卸载过程的不可逆，产生能量耗散，引起黏着接触滞后.因此，有必要进一步分析探针样品作用力，以期对AFM失稳特性和力曲线测量(或接触分离过程)中的能量耗散有更明确的认识.

图2 AFM微梁、探针、样品系统简化模型Fig.2 A simpli fi ed model for the system of AFM cantilever,tip and sample

图3 黏着图[21]Fig.3 Adhesion map[21]

AFM探针尖端为椎球状，其球形部分半径一般在几纳米到几十纳米之间，因此探针与样品的接触分离为微纳尺度接触问题.经典微尺度黏着接触理论有Bradley理论、DMT理论、JKR理论和M-D理论等[11,13].Johnson和Greenwood利用Maugis理论绘制了弹性接触的黏着作用分布图，也称黏着图[21]，如图3所示.图中各边界的意义在文献中有较详尽的表述.实际的接触适用于何种接触理论，由两个无量纲参数决定.一个是载荷参数为外载荷，R是两接触物体的等效半径，w是界面能；另外一个是弹性参数，它和Tabor数µ等价.从黏着图中看出，黏着力与整个载荷比值取0.05是经典弹性接触与黏着弹性接触的临界点，当比值小于0.05时，表明黏着力相对于整个载荷非常小，可以忽略黏着力的影响，而采用Hertz接触模型.相反，当比值大于0.05时，就必须考虑黏着力的影响而采用黏着接触模型.黏着接触模型的选取由第二个无量纲数(弹性参数)控制.此弹性参数详细的论述可参考Johnson等[21]的文章.

Tabor数µ的定义为

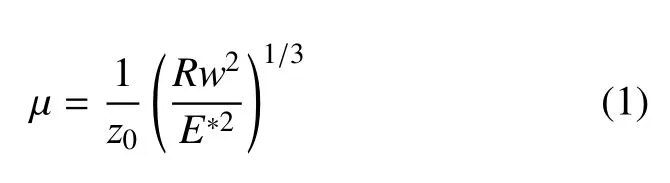
其中，z0为原子间平衡间距.R=R1R2/(R1+R2)为两接触物体的等效半径，R1，R2为两接触物体的半径，对AFM来说，样品为无限大平面，故R就是AFM针尖半径.为接触区等效弹性模量，Ei，υi(i=1,2)分别为样品和探针的弹性模量和泊松比.AFM探针针尖一般为Si或Si3N4材料，其弹性模量分别为168GPa和310GPa，泊松比为[22]0.22.对于比较刚硬的样品，即弹性模量大于探针材料的，等效弹性模量接近于探针材料的弹性模量，对于比较软的材料，如生物材料、聚乙烯(PE)、聚二甲基硅氧烷(PDMS)等，弹性模量取值在500Pa∼50GPa之间，这时等效弹性模量取值接近样品材料.界面能一般取[20]1∼102mJ·m−2.对 Tabor数进行估计，E*在 103Pa∼102GPa之间取值，z0=0.5nm，R=50nm.这样µ在3.4×10−3∼ 1.6×104之间取值.因此，不同的样品和探针，其微尺度接触模型可取图3中所有理论.根据Greenwood等的研究[14,23],当µ>5时，JKR接触理论模拟微尺度接触时是非常合适的.对于上述各参数，在E*和w取上述变化范围时，给出了JKR适用区域，如图4所示.随着界面能量的增大，特别是样品变软时，JKR模型是合适的.因此下面的微尺度接触模型用JKR理论.

相比较于Hertz理论，实际的弹性体接触界面间除了有相互的斥力外，在物理本质上还应当引入分子间的引力作用，如范德华力，其统计学上的表现就是表面能.表面能的引入，势必会增大接触面积，这样也要重新考虑压入量和储存的弹性能.对这个问题，Johnson等[24]提出了JKR接触模型.相应的方程如下

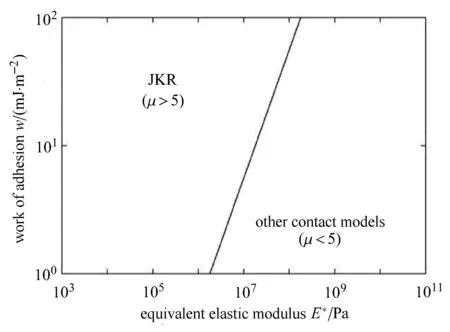
图4 JKR模型使用区域Fig.4 The boundary of validity of JKR model

其中，a是在外载F作用下的接触半径.当没有黏着力的影响，即w=0时，上述表达式退化为Hertz弹性接触理论.

外载F作用下两弹性体的压缩或拉伸量为

式(2)和式(3)中F,a和δ如图2(b)和图2(c)所示.外载F可取的最小值为该力为把探针从样品上拉离所需要的最大力，称为黏附力Fad

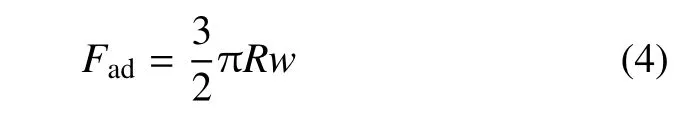
另外如果把接触问题类比于裂纹扩展，则黏附力Fad对应于恒力加载模式下的裂纹失稳问题，同样对应于恒位移模式下的失稳，可得到此时两接触物体拉开的最大位移量为[25]

对应的拉力为

通过式(2)和式(3)，并把外载和位移无量纲化，得到JKR理论加卸载曲线如图5所示[26].

图5 JKR模型加卸载曲线Fig.5 The loading and unloading curves of JKR model

从图5可以看到，JKR理论同样存在两个失稳过程，第一个失稳为突跳接触失稳(jump in)，如图OA段.第二个失稳为分离失稳(jump out)，这个失稳相对复杂些.从图5可以看到两个极限位置C和D，C点力梯度为0，D点力梯度为无限大.由上面力学失稳分析知，当图2(b)中弹簧刚度kc趋近于无穷小时，失稳发生在图5的C点，当图2(b)中弹簧刚度kc趋近于无穷大时，失稳发生在图5的D点.实际AFM微悬臂梁具有确定的刚度，因此探针与样品分离位置处于图5曲线CD间.依据JKR理论，C点为分离时取最大力的位置，D点为分离取最小力的位置，随着图2中微悬臂梁刚度提高，分离力逐渐变小.

因此，从图5可以看出,曲线CD是AFM探针与样品分离时的状态区间，探针样品分离点位于CD曲线上力梯度等于微悬臂梁刚度处.探针样品分离时分离力F的范围为

AFM力曲线实验证明上述结论，图6是AFM力曲线，样品为疏水硅片和杨氏模量为200MPa的PDMS，悬臂梁刚度分别为 0.06N/m，0.12N/m，图6(a)是刚度为0.06N/m的探针在疏水硅片上的力曲线，其失稳点发生在最大拉力处.图6(b)和图6(c)所用样品为PDMS，微悬臂梁刚度分别为0.06N/m，0.12N/m，可以看出随着微悬臂梁刚度增大，分离时的力逐渐减小，证明了上面对分离失稳判据的分析.

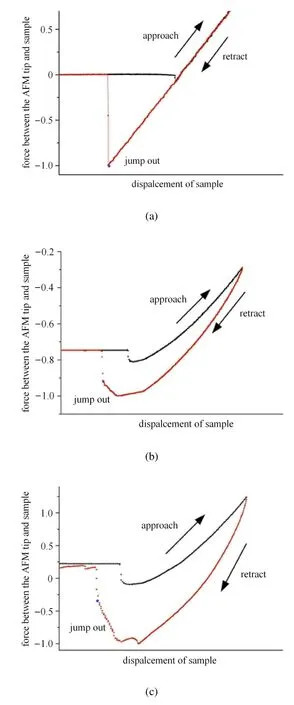
图6 AFM力曲线Fig.6 Force curve for di ff erent cantilever

AFM轻敲模式下，探针样品间接触分离过程的能量耗散对高度像和相位像都有非常大的影响，特别是相位像直接与耗散能相关.下面用JKR理论讨论探针样品接触分离过程中的能量耗散.由图5可以看出，接触分离过程中的耗散能是指在接触分离一个周期中外力所做的功.如果微悬臂梁较软，分离失稳发生在C点，则外力功为

式中A1为图5中的阴影面积.

如果微悬臂梁较刚硬，分离失稳发生在D点，则外力功为

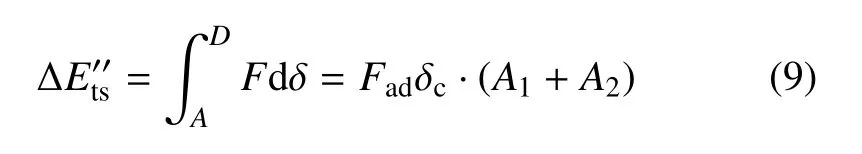
式中A2为图5中的阴影面积.通过数值计算，A1=1.07，A2=0.47.定义一个参照能量∆E=Fadδc，由式(5)和式(6)得

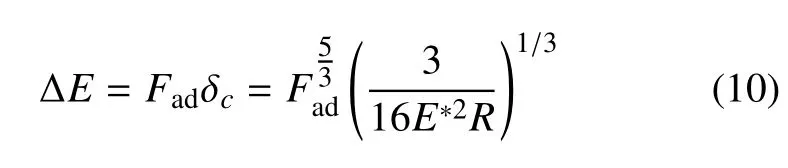
因此，基于JKR接触模型下的能量耗散Ets为(1.07∼1.54)∆E.下面估算耗散能的大小，假定耗散能为∆E.一般情况下，AFM探针半径为50nm，考虑毛细力影响，其黏附力约为4πRγ，值约为40nN(γ取为水的表面张力).在无毛细力作用下，黏附力要降低一个量级，为4nN.接触区域的等效杨氏模量从上述表达式可以看出接近两接触材料中最软材料的杨氏模量，等效弹性模量E*取值在103Pa∼102GPa之间，则耗散能 ∆Ets在 (8×10−20∼ 1.6×10−14)J之间.

2 粗糙度对能量耗散的影响

真实的接触表面都不可能达到原子级光滑，因此有必要考虑粗糙度对AFM加卸载曲线和接触分离过程能量耗散的影响.如图2所示，将AFM探针样品接触简化为半球与半无限大平面的接触模型，如果再考虑球面和半无限大平面的粗糙度，会引起数学处理上的不方便，为方便处理，假定问题为两半无限大平面的接触，其中一个平面假定为光滑平面，另一个为粗糙平面，如图7所示.

图7 粗糙弹性表面与光滑刚性表面接触模型Fig.7 Contact model of elastic roughness surface with a rigid flat surface

假设图7下平面粗糙峰高度符合高斯分布，即

其中，z为高度，φ(z)为粗糙峰高度的概率密度函数，所有的粗糙峰都假设为半径为R的半球，同图2，σ为高度分布标准差.

假设单峰与平面接触分离用JKR模型，其加卸载曲线为图5所示.假设失稳发生在D点，可以得到载荷变形关系的隐式表达[26]

如图7所示，先考虑接触过程，当光滑平面压入到距离粗糙平面平均线为d时，如果假设整个粗糙平面有N个尖峰，则此时共有个尖峰与光滑平面接触.同时参照图5和式(12),可得加载方程

其中，δ=z−d，∆=δ/σ，∆c=δc/σ，h=d/σ.同理，考虑卸载，当光滑平面与粗糙平面处于图7位置时，卸载方程为

从图8可以看出，粗糙度对加卸载曲线的影响较大，随着粗糙比的变大，加卸载路径逐渐趋于重合，接触分离中的黏附性能消失.特别是对加卸载曲线围成的面积，即能量耗散，影响较大.定义能量耗散∆Ets

通过对式(15)或图8进行数值积分，得到能量耗散与粗糙度的关系如图9所示.

从图9可以看出，当粗糙度变大时，会降低接触分离的耗散能量，因此，在轻敲模式的扫描图象中，表面粗糙度对高度像和相位像都有一定的影响，并可能引起赝像.

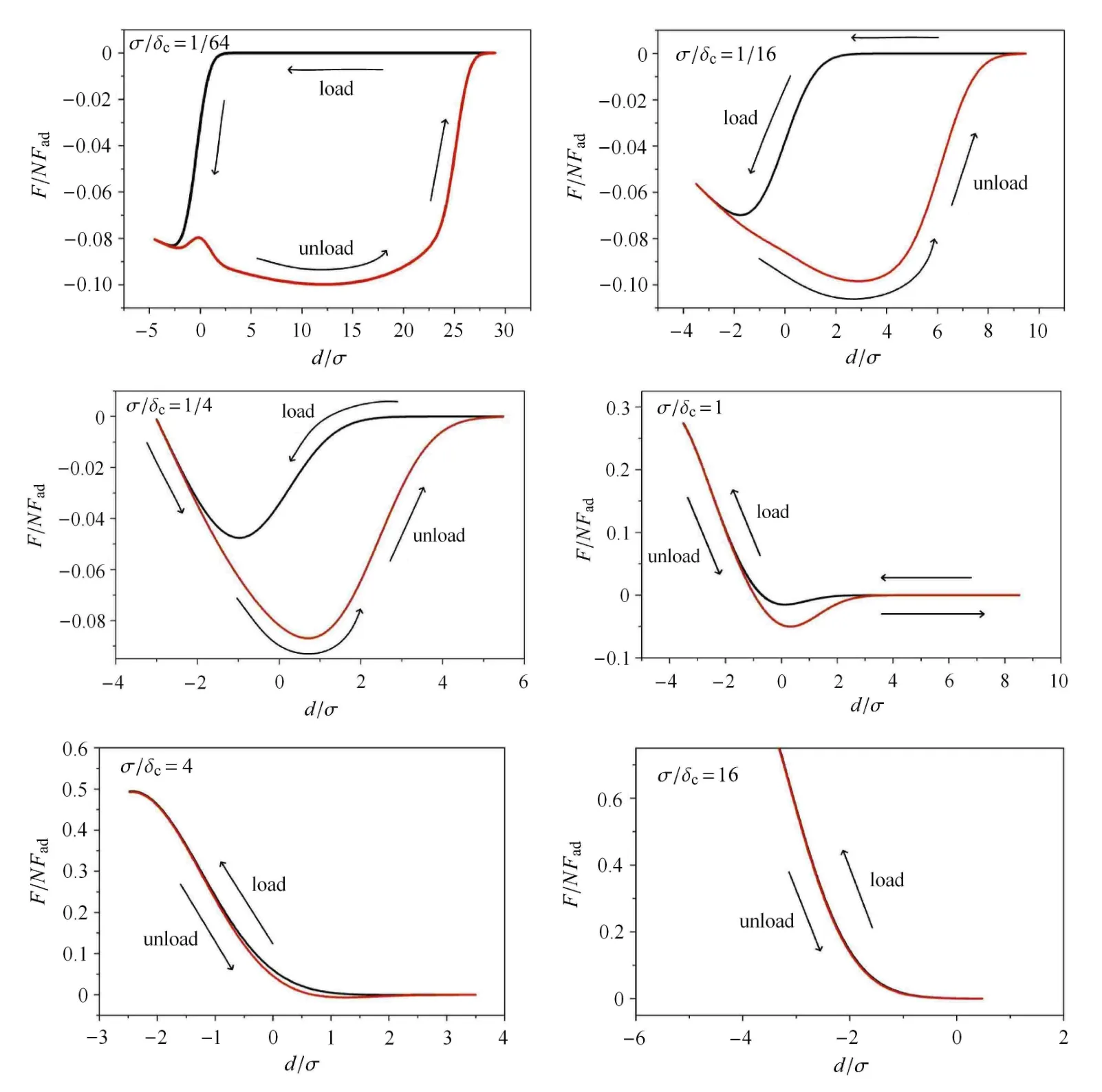
图8 粗糙度对加卸载曲线的影响Fig.8 The e ff ect of roughness on loading and unloading curves

图9 粗糙度对加卸载过程能量耗散的影响曲线Fig.9 The relationship between energy dissipation and surface roughness in loading unloading process

3 液桥对能量耗散的贡献

大气环境下，若样品是亲水的，AFM探针与样品之间的作用力中的主导力为毛细力，它比其他作用力(范德华力、静电力等)大1∼2个量级[17].因此，有必要考虑湿度对探针样品接触分离过程中能量耗散的影响.探针与样品间的毛细力是由探针与样品间的液桥提供的.作者对AFM中液桥的生成和破碎进行过较深入的研究，关于液桥的生成，我们提出了以下模型：挤出模型、毛细凝聚模型和液膜流动模型.下面简要介绍这3个模型[27-33].

在大气环境中，亲水样品表面会吸附一层或多层水分子进而形成水膜，在探针接触样品时，探针和样品表面的水膜被挤出，这部分挤出的水形成液桥，由于这部分挤出水体积较小，按照热力学理论，此时的液桥还不是最终平衡态时的液桥，挤出模型形成液桥的特征时间等于探针样品的接触时间.

在探针与样品接触后，探针与样品接触区域附近的狭缝区具有极强的吸附能力，这种强吸附势会使得狭缝区空气中的水分子产生凝聚，这个过程很快完成，狭缝区外围的水分子要通过扩散运动到狭缝区再行凝聚，扩散过程相对于凝聚过程需要更长时间，因此毛细凝聚形成液桥的特征时间实际上是由扩散过程控制的.

另外，由于液桥中的负压和样品水膜中的分离压作用，液桥远处的水膜向液桥流动，这个流动模型的特征时间由流动过程控制.

由热力学关系，水膜厚度h与相对湿度有如下关系[33]

式中哈梅克常数AH= −8.7×1021J，水的摩尔体积Vm=1.8×10−5m3/mol，普适气体常数=8.31J/(K·mol)，取绝对温度=293K，p为大气蒸汽压，ps为液体饱和蒸汽压.p/ps为相对湿度.在相对湿度为65%时，h=0.2nm.

在AFM轻敲模式下，微悬臂梁以接近于自身一阶共振频率(10∼500kHz)的频率振动且每一周期内探针敲击样品一次，针尖与样品每次的接触时间为

式中,A为微悬臂梁振幅，h为液膜厚度，T为微悬臂梁振动周期.悬臂梁振动频率取为100kHz，A=10nm，h=0.2nm(相对湿度为 65%).振动周期为10−5s，则得tcontact?0.2µs.

文献[32]曾详尽计算了相对湿度为65%的各液桥生成模型对液桥的贡献，在轻敲模式下，由于探针样品接触时间在微秒量级以下，毛细凝聚的特征时间为毫秒量级，液膜流动的特征时间为102µs∼102s，因此毛细凝聚和液膜流动对液桥贡献较小，液膜挤出在轻敲模式下占主导地位.

如图10所示，假设探针和样品表面吸附水膜厚度为h，忽略探针样品接触后的弹性变形，则挤出液体体积即液桥体积为

式中h?R.则由式(16)和式(18)可得不同湿度下由挤出效应所形成液桥的体积.实验和理论证明，图10(b)液桥在拉断时的临界长度Dcr正比于液桥体积的立方根[33].

由图10(b)可以看出，液桥毛细力由液桥表面张力和液桥内外的杨--拉普拉斯压力差组成

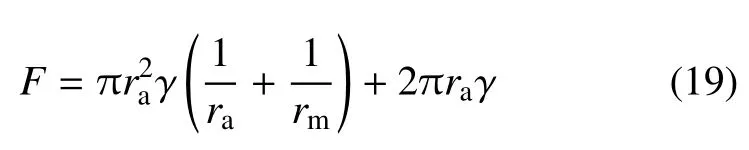
式中，ra，rm为液桥的主曲率半径，则在轻敲模式下，由挤出效应形成的液桥，在极短时间内被拉断，这个过程为等容绝热过程，外力克服毛细力做功即有液桥引起的耗散能为

图10 AFM液桥模型Fig.10 The liquid bridge in AFM

式(19)和式(20)联合求解，就可得到不同湿度下耗散能.由于在轻敲模式下，液桥等容变化，其几何形态复杂，在求解过程中利用了圆弧近似，所求得的毛细力与实验比较吻合.详细求解可参考文献[31-33]，其耗散能与相对湿度的关系见图11.

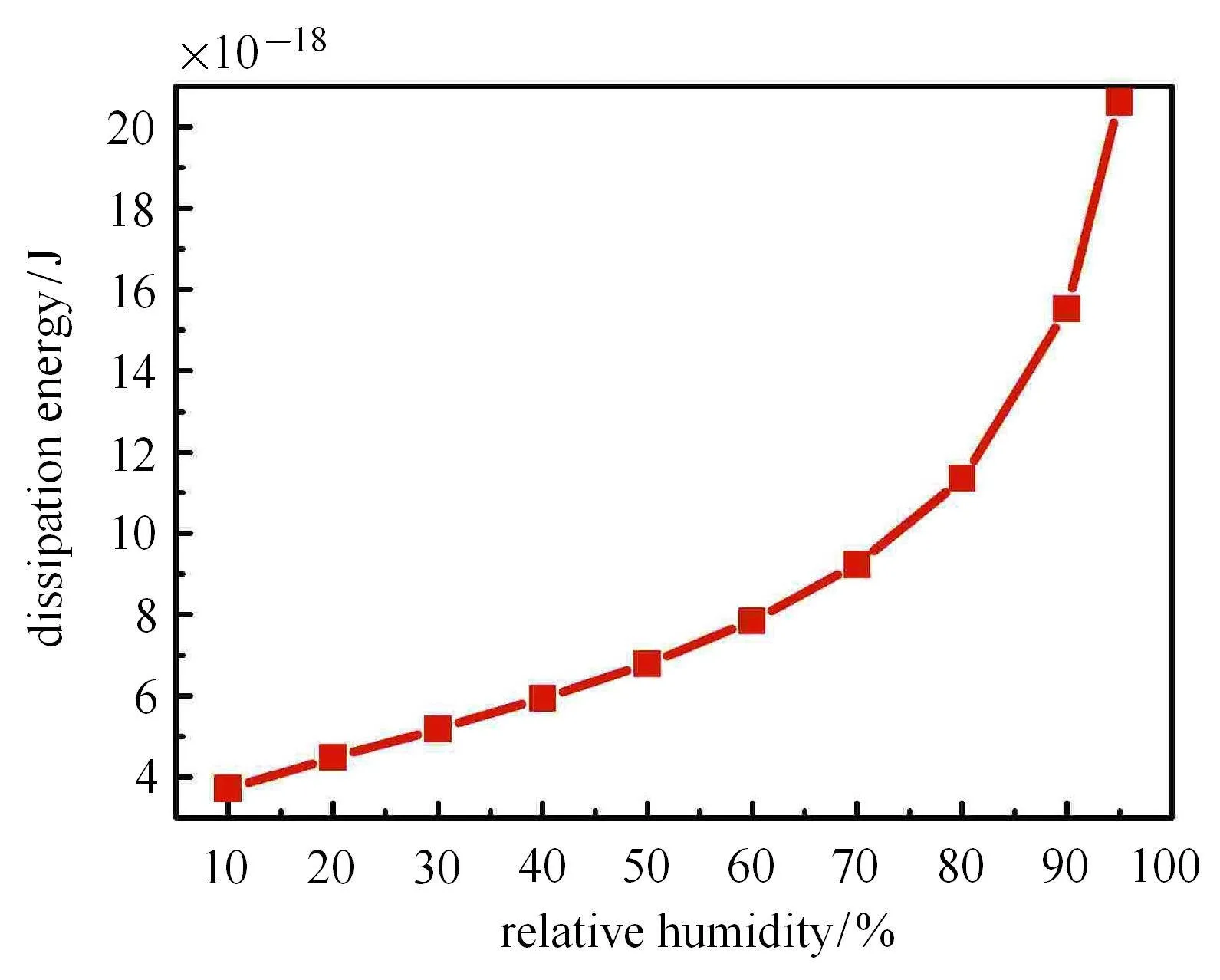
图11 耗散能与相对湿度之间的关系Fig.11 The relationship between energy dissipation and relative humidity

从图11可以看出，湿度对探针半径为50nm的AFM来说，在轻敲模式下，耗散能随相对湿度升高而增大，液桥断裂能即耗散能大约在10−18∼8×10−17J量级.

4 讨论

4.1 能量耗散对轻敲模式下相位影响

对于图2和图10所示的简化模型，表明无论是否考虑毛细力的影响，在接触分离的过程中都会产生能量耗散.由于轻敲模式的AFM是在高频振动状态下工作，当考虑能量耗散影响后，相当于在振动系统中引入阻尼机制，现在我们知道在一个振动周期内，如果能量耗散为∆E，由于AFM为单频激励单频响应，故将探针样品系统简化为一维阻尼振子系统，如图12所示.弹簧刚度为探针样品间作用，在本文中它既可是式(12)中JKR黏附力也可以是式(19)中的毛细力，这里总弹簧刚度计及了探针样品作用力的贡献.按照阻尼能量等效原则，图12系统在一个周期内，阻尼器所耗散的功就是上述JKR模型或液桥所引起的耗散能.图12振子系统振动方程为

其中，m为微悬臂梁的等效质量，

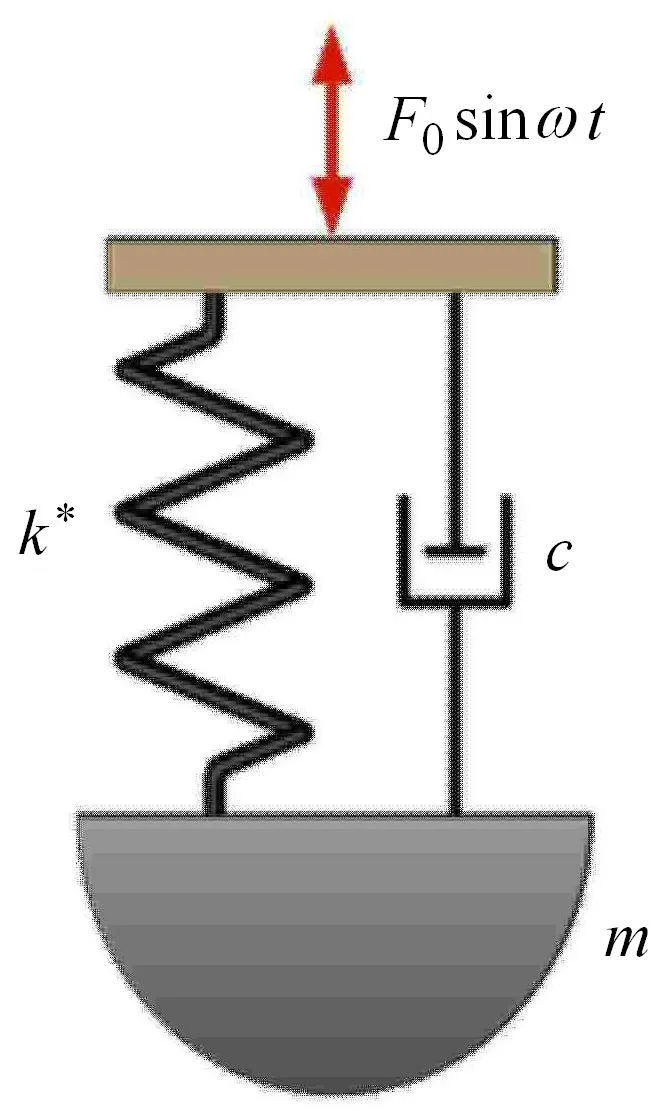
图12 AFM轻敲模式简化振动系统Fig.12 The simpli fi ed oscillator system of tapping AFM

因此，由耗散能所引起的相位差φ正切为[12]

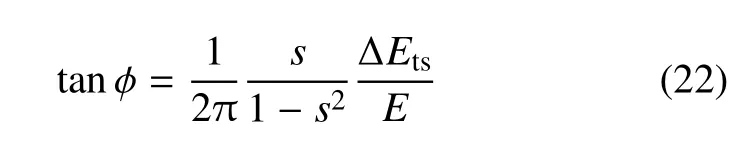
式中，E为系统总能量，s为激振频率与系统固有频率比，在轻敲模式下，s?1±ε，ε为一小量，因此式(22)简化为

式(23)中有正负号是由于轻敲模式下激振频率选在微悬臂梁固有频率附近，依据不同样品和目的，激振频率可小可大，如果激振频率小于固有频率，相位在[0,π/2]区间，如果激振频率大于固有频率，相位在[π/2,π]区间.

4.2 黏附、表面粗糙度、环境湿度对相位的影响

我们采用JKR模型对微纳尺度下接触分离过程能量耗散进行分析，得到能量耗散∆Ets为(1.07∼由式 (23)可以看出，对于疏水样品或干燥环境下的亲水样品，即不考虑毛细力影响时，轻敲模式下的相位图反映的是探针样品的界面能和样品的软硬程度，因此在样品表面，如果不同区域的物质构成不同，则其界面能和杨氏模量是不同的，在相位图上是能够分辨出来的.如果式(23)中s<1，则界面能越高，能量耗散越大，得到的相位也越大；同样，如果样品杨氏模量比较高，则能量耗散比较小，相位就比较小.

从图9可以看出，表面粗糙度越大，针尖样品间的能量耗散越小.如果还是假设s<1，从式(23)可以看出，相位要变小，这种情况下，我们就不能判断这个区域相位变小是什么原因引起的.由上面分析，我们知道相位变小的原因也有可能是界面能变小或样品模量提高.但一般情况下，这种相位的变化，被认为是样品物理化学性质的变化引起的，而不会认为是样品形貌引起相位变化，进而引起扫描图像解读的误差，这也是赝像的一种表现形式.

在大气环境下的亲水样品，从图11看出，随着相对湿度的升高，耗散能在升高，从式(23)可看到，当激振频率稍低于梁固有频率时，随湿度增高，相位增大，当激振频率稍高于固有频率时，随湿度增高，相位减小.因此，同一个样品，当我们在不同的实验室环境下扫描时，会得到不同的相位图，但不管相位随湿度怎么变化，真实的样品特性是固定的，因此，我们认为湿度干扰了我们对相位图的正确分析，带来了样品的赝像.

4.3 塑性、黏弹性对耗散的贡献

在轻敲模式下，由于微悬臂梁的振动频率很高，在样品的一个扫描点，探针与样品接触分离大于103次，因此除了探针样品的第一次接触会在接触区产生塑性变形外，其他后续接触可以忽略塑性效应，因此可以认为在轻敲模式下，塑性变形对耗散没有影响.关于材料黏弹性对耗散的影响，由于探针速度约为2πAf，A为微悬臂梁振幅，取10nm，f为激振频率，取105Hz，则探针速度在10−2m/s量级，在这种低速冲击下，是否考虑黏性的影响，是一个可商榷的问题，留待以后讨论.

5 结论

AFM轻敲模式下相位成像是研究物质表界面特性的重要手段，其相位主要反映的是探针样品作用时的能量耗散.本文主要就两类接触进行了研究.一类是不考虑毛细力影响的微纳尺度接触能量耗散问题，一类是考虑毛细力下的接触能量耗散问题.

在不考虑毛细力存在的情况下，采用JKR接触模型，提出了AFM力曲线中分离失稳与JKR加卸载曲线中的对应位置关系，进而计算轻敲模式下的能量耗散.采用一维振子模型，探讨影响相位的样品因素.并进一步探讨了粗糙度对能量耗散的影响，并指出粗糙度是引起赝像的原因.

通过对液桥生成机理分析，对比挤出、毛细凝聚和液膜流动在液桥生成过程所需平衡时间与探针样品接触时间，认为在轻敲模式下，只有挤出效应对液桥的生成有贡献.由于探针样品接触时间极短，因此在等容条件下，计算了不同湿度下的接触能量耗散.进而利用简单的一维振子模型，提出相对湿度影响样品相位图，指出环境相对湿度是引起样品赝像的原因.

1 Binnig G.Atomic force microscope.Physical Review Letters,1986,56(9):930-933

2 Binnig G,Rohrer H.In touch with atoms.Reviews of Modern Physics,1999,71(2):s324-s330

3 Giessibl FJ.Advances in atomic force microscopy.Reviews of Modern Physics,2003,75(3):949-983

4 Zhong Q,Inniss D,Kjoller K,et al.Fractured polymer silica fi ber surface studied by tapping mode atomic force microscopy.Surface Science,1993,290(1-2):L688-L692

5 Grutter P,Zimmermann-Edling W,Brodbeck D,et al.Tip artifacts of microfabricated force sensors for atomic force microscopy.Applied Physics Letters,1992,60(22):2741-2743

6 Gan Y.Atomic and subnanometer resolution in ambient conditions by atomic force microscopy.Surface Science Reports,2009,64(3):99-121

7 Edwards H,McGlothlin R,Elisa U,et al.Vertical metrology using scanning probe microscopes:Imaging distortions and measurement repeatability.Journal of Applied Physics,1998,83(8):3952-3971

8 Ohnesorge FM.Intricate stepline artifact can mimic true atomic resolution in atomic force microscopy.Physical Review B,2000,61(8):5121-5124

9 Morton DN,Roberts CJ,Hey MJ,et al.Surface characterization of caramel at the micrometer scale.Journal of Food Science,2003,68(4):1411-1415

10 徐金明,白以龙.原子力显微镜形貌测量偏差的机理分析及修正方法.力学学报,2011,43(1):112-121(Xu Jinming,Bai Yilong.Analysis of topography measurement error in atomic force microscope(AFM)and its revision method.Chinese Journal of Theoretical and Applied Mechanics,2011,43(1):112-121(in Chinese))

11 赵亚溥.纳米与介观力学.北京:科学出版社,2014(Zhao Yapu.Nano and Mesoscopic Mechanics.Beijing:Science Press,2014(in Chinese))

12 Garc´ıa R,P´erez R.Dynamic atomic force microscopy methods.Surface Science Reports,2002,47(6-8):197-301

13 郭万林,台国安,姜燕.针尖的化学物理力学研究.力学进展,2005,35(4):585-599(Guo Wanlin,Tai Guoan,Jiang Yan.Rresearch on probe’s chemical and physical mechanics.Advances inmachanics,2005,35(4):585-599(in chinese))

14 李喜德.探针实验力学.实验力学,2007,22(3):217-228(Li Xide.Probe exprimental mechanics.Journal of Exprimental Mechanics,2007,22(3):217-228(in Chinese))

15 Qian J,Lin J,Shi M.Combined dry and wet adhesion between a particleandanelasticsubstrate.JournalofColloid&InterfaceScience,2016,483:321-333

16 陈少华,彭志龙,姚寅.表面黏附及表面输运的最新研究进展.固体力学学报,2016,37(4):291-311(Chen Shaohua,Peng Zhilong,Yao Yin.The latest research progress in surface adhesion and transportion.Chinese Journal of Solid Mechanics,2016,37(4):291-311(in Chinese))

17 Drake B,Prater CB,Weisenhorn AL,et al.Imaging crystals,polymers,and processes in water with the atomic force microscope.Science,1989,243(4898):1586-1589

18 Anczykowski B,Cleveland JP,Krger D,et al.Analysis of the interaction mechanisms in dynamic mode SFM by means of experimental data and computer simulation.Applied Physics A,1998,66(1):885-889

19 Garc´ıa R,Tamayo J,Calleja M,et al.Phase contrast in tappingmode scanning force microscopy.Applied Physics A,1998,66(1):309-312

20 Israelachvili JN.Intermolecular&Surface Forces.America:Academic Press,2011

21 Johnson KL,Greenwood JA.An adhesion map for the contact of elastic spheres.Journal of Colloid&Interface Science,1997,192(2):326-333

22 Xu D,Liechti KM,Ravichandar K.On the modi fi ed tabor parameter for the JKR-DMT transition in the presence of a liquid meniscus.Journal of Colloid&Interface Science,2007,315(2):772-785

23 Greenwood JA.Adhesion of elastic spheres.Proceedings Mathematical Physical&Engineering Sciences,1997,453(1961):1277-1297

24 Johnson KL,Kendall K,Roberts AD,et al.Surface energy and the contact of elastic solids.Proc R Soc London A,1997,324,301-313

25 Maugis D.Adhesion of spheres—the JKR-DMT transition using a Dugdale model.J.Colloid Interface Sci,1992,150(1):243-269

26 Wei Z,He MF,Zhao YP.The e ff ects of roughness on adhesion hysteresis.Journal of Adhesion Science and Technology,2010,24(6):1045-1054

27 Wei Z,Zhao YP.Experimental investigation of the velocity e ff ect on adhesion forces with an atomic force microscope.Chinese Physics Letters,2004,21(4):616-619

28 WeiZ,ZhaoYP.GrowthofliquidbridgeinAFM.JournalofPhysics D-Applied Physics,2007,40(40):4368-4375

29 Wei Z,He MF,Zhao WB,et al.Thermodynamic analysis of liquid bridge for fi xed volume in atomic force microscope.Science China Physics,Mechanics&Astronomy,2013,56(8):1962-1969

30 Wei Z,Sun Y,Ding WX,et al.The formation of liquid bridge in different operating modes of AFM.Science China Physics,Mechanics&Astronomy,2016,59(9):611-694

31 魏征,陈少勇,赵爽等.原子力显微镜中等容液桥的毛细力分析.应用数学和力学,2014,35(4):364-376(Wei Zheng，Chen Shaoyong，Zhao Shuang,et al.Capillary force analysis of constantvolume liquid bridges in atomic force microscropes.Applied Mathematics and Mechanics,2014,35(4):364-376(in Chinese))

32 魏征,赵爽,陈少勇等.原子力显微镜中液桥生成机理探讨.应用数学和力学,2015,36(1):87-98(Wei Zheng,Zhao Shuang,Chen Shaoyong,et al.Study of growth mechanisms for the liquid bridge in atomic force microscopes.Applied Mathematics and Mechanics,2015,36(1):87-98(in Chinese))

33 陈少勇,魏征.原子力显微镜轻敲模式下由液桥引起的能量耗散.力学与实践,2015,37(5):585-589(Chen Shaoyong,Wei Zheng.The dissipation energy in tapping mode of atomic force microscope due to liquid bridge.Mechanics in Engineering,2015,37(5):585-589(in Chinese))

ENERGY DISSIPATION IN TAPPING MODE ATOMIC FORCE MICROSCOPY1)

Wei Zheng*,2)Sun Yan*Wang Zairan*Wang Kejian*Xu Xianghong†
*(College of Mechanical and Electrical Engineering，Beijing University of Chemical Technology，Beijing100029，China)
†(State Key Laboratory of Nonlinear Mechanics，Institute of Mechanics，Chinese Academy of Sciences，Beijing100190，China)

There are many imaging modes in atomic force microscopy(AFM),in which the tapping mode is one of the most commonly used scanning methods.Tapping mode can provide height and phase topographies of the sample surface,inwhichphasetopographyre fl ectsmorevaluableinformationofsamplesurface,suchassurfaceenergy,elasticity,hydrophilic hydrophobic properties and so on.According to the theory of vibration mechanics,the phase is related to the energy dissipation of the vibration system.The dissipation energy between the tip and sample in tapping mode of AFM is a very critical key to understanding the image mechanism.It is a ff ected by sample properties and lab environment.The loading and unloading curves of tip and sample interaction are given based on the JKR model while the capillary force is not considered.The unstable position of jump out between the tip and sample is show，and then the energy dissipation in a complete contact and separate process is calculated.The e ff ect of roughness of sample surfaces on energy dissipation is also discussed.It is provided that the extrusion e ff ect is the dominant fact or in liquid bridge formation by characteristic time contrast when capillary force is considered in tapping mode AFM.The e ff ects of relative humidity on energy dissipation are numerically calculated under isometric conditions.Finally,the relationship between phase image of AFM and sample surface energy,Young’s modulus,surface roughness and relative humidity is brie fl y explained by one-dimensional oscillator model.The analyses show that the di ff erence of surface roughness and ambient humidity can cause phase change,and then they are considered as the cause of artifact images.

atomic force microscope,phase image,adhesion,liquid bridge,energy dissipation,capillary force

TH742.9

A doi：10.6052/0459-1879-17-223

2017–06–16 收稿，2017–09–08 录用,2017–09–08 网络版发表.

1)国家自然科学基金(11572031)和非线性力学国家重点实验室开放基金资助项目.

2)魏征，副教授，主要研究方向：微纳米力学.E-mail:weizheng@mail.buct.edu.cn

魏征，孙岩，王再冉，王克俭，许向红.轻敲模式下原子力显微镜的能量耗散.力学学报,2017,49(6):1301-1311

Wei Zheng，Sun Yan，Wang Zairan,Wang Kejian,Xu Xianghong.Energy dissipation in tapping mode atomic force microscopy.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1301-1311