基于解除约束原理推导一阶非完整约束系统的Lagrange方程
高普云
(国防科技大学 空天科学学院,湖南 长沙 410073)
基于解除约束原理推导一阶非完整约束系统的Lagrange方程
高普云
(国防科技大学 空天科学学院,湖南 长沙 410073)
基于解除约束原理,从达朗贝尔原理出发推导一阶非完整约束系统的运动方程。通过引进新的位移参数解除非完整约束,使非完整约束系统成为无约束系统,进而推导出系统的不带乘子的全新的Lagrange方程。
解除约束;非完整约束系统;Lagrange方程;位移参数;无约束系统
1 研究背景
自从1894年H. R. Hetrz 引入非完整约束系统这一概念以来,许多力学家和数学家在这一方面做了大量工作[1]。然而,非完整约束系统运动方程的推导一直处于争议之中[2],其中有如下两种观点。
一种观点认为,虚位移应满足 Appell-Ч е т а е в定义[3]。设qk(k=1, 2, …, n)是系统的广义坐标,则系统的一阶非完整约束可表示为

按 Appell-Ч е т а е в定义,加在虚位移上的条件是

对于完整约束系统,这个条件自动成立,因为完整约束系统的约束不含广义速度,其对广义速度的偏导数为零。
从变分角度来讲,加在虚位移上的条件是

式(2)与式(3)完全不同。著名的数学力学家V. I.Arnold认为条件(2)是人为加上去的,因为利用条件(2)推导出来运动方程的解会出现“怪行为”[4]。
另一种观点认为,由于最优控制问题可看作非完整约束系统,最优控制问题的控制方程的推导是从式(3)出发的,因此应从式(3)出发推导运动方程[5-7]。
利用约束自身的特点,文献[8-10]通过解除约束的方法推导出了3类特殊的一阶非完整约束系统的不带乘子的Lagrange方程。本文通过引进新的位移参数解除非完整约束,使非完整约束系统成为无约束系统;再按照完整约束系统推导运动方程的方法,推导出一阶非完整约束系统的不带乘子的Lagrange方程。
2 一阶非完整约束系统不带乘子的Lagrange方程
2.1 引进新的位移参数解除非完整约束
通过3个实例,介绍怎样引进新的位移参数来解除非完整约束。
例1 斜面冰橇问题。
该问题对应系统的Lagrange函数[11]为

式中:(x, y)是冰刀与斜面接触点的坐标;
k为回转半径;
φ为冰刀与Ox轴的夹角;g为重力加速度;α为斜面的倾角。系统的约束方程为


式中:z为积分变量;t为时间。
系统的Lagrange函数(4)变为

因此,这个系统变成以新位移参量u和φ为独立变分变量的无约束系统。
根据达朗贝尔原理,这个系统的运动应使得泛函的变分为零,即δI=0。式中t1为积分常数,它由初始条件决定。

通过直接计算得

因为δu与δφ是相互独立的,由δI=0可得

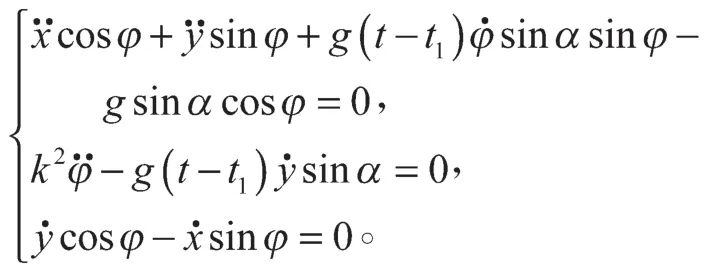
例2 均质球在粗糙的圆锥面内纯滚动问题。
该问题对应系统的Lagrange函数[11]为

式中:m为球的质量;
r为球与圆锥面的接触点到圆锥顶点的距离;
α为半锥角;
a为球的半径;
γ为两平面的夹角;
k为回转半径;
φ, χ+γ, θ为 3 个欧拉角。系统的约束方程为

由式(9)可得

对式(10)积分得
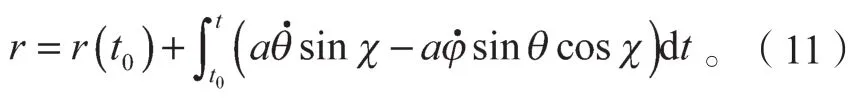
由式(8)和式(11)可得

因此,该系统的2个约束被解除,从而系统成为无约束系统,可以按例1的方法推导其运动方程。
例3 三粗糙均质圆柱体问题。
该问题对应系统的Lagrange函数[11]为
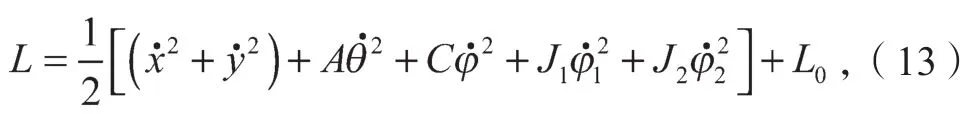
式中:(x, y)为上圆柱质心的两水平坐标;
A为上圆柱绕通过中心铅垂轴的转动惯量;
C为上圆柱绕通过中心轴的转动惯量;
θ为上圆柱母线与Ox轴的夹角;
J1, J2分别为下面两圆柱对于母线的转动惯量;
φ为上圆柱的转角;
φ1, φ2为下面两圆柱的转角;
L0为常数。
系统的约束方程为

式(14)~(17)中:R为上面圆柱的半径;
r为下面两圆柱的半径;
a为常数;
α为下面两圆柱母线的夹角。
由式(14)和式(15)可得

由式(16)和式(17)可得

由式(18)和式(20)可得

因此有

式中u是引进的位移参数。
由式(18)和式(22),如果还引进位移参数v使得

就解除了约束式(18)(20)。
由式(19)(22)(23)可得

因此,约束式(19)被解除。
由式(19)(21)(22)可得

由式(18)和式(22),通过积分可得


利用式(27)和式(23)可得

综合式(28)和式(22)~(24)可得


因此,该系统的所有约束被解除。
从上面3个例子可以看出,可通过引进位移参数u1, u2, …, un-h,从约束方程中解出式中:;

是由约束条件决定的关于时间、新位移变量及其导数的函数。
2.2 推导不带乘子的Lagrange方程
将 式(29) 代 入 系 统 的Lagrange函 数(其中)可得

其中

根据达朗贝尔原理,这个系统的运动应使得作用泛函

的变分为零。事实上,在本文的3个例子中,Lagrange函数只含有一重积分,即可写成

的形式,从而作用泛函变为
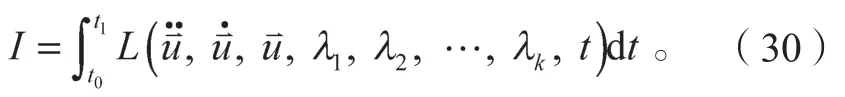
下面只从式(30)出发推导Lagrange方程。对于一般情况,只给出Lagrange方程,而不给出详细的推导过程。
对式(30)求变分得
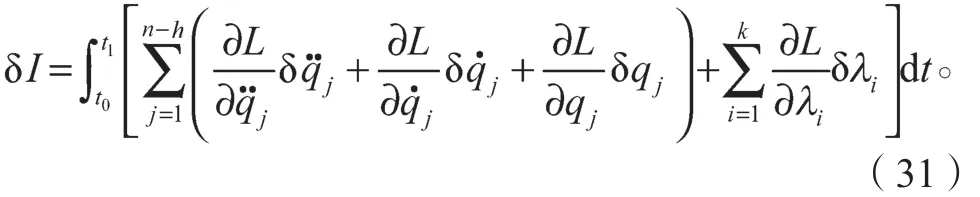
为了方便,记


利用分部积分法可得


由式(31)~(33)可得

由δI=0得到系统的运动方程为
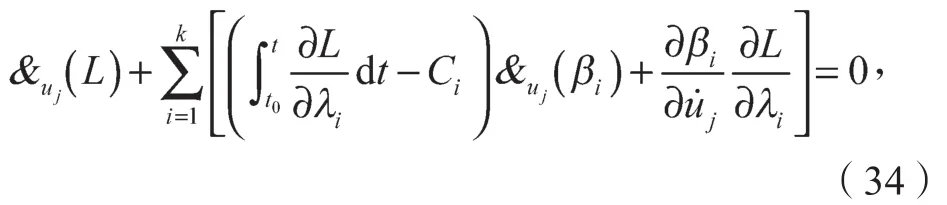
式中:i=1, 2, …, n-h;Ci是积分常数。
对于一般情况,系统的运动方程为
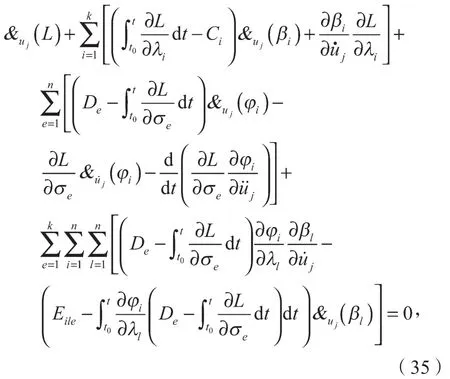
式中Ci, De和Eile是积分常数,它们由初始条件决定。
如果Lagrange函数中不含σi,那么式(35)退化为式(34)。
可以直接用式(34)推导出例1~3的运动方程,这些直接的计算从略。
3 结论
通过引进新位移变量解除非完整约束,使非完整约束系统成为无约束系统。对于无约束系统,不需要考虑加在虚位移上的条件,从而完全可以按完整约束系统的方法来推导非完整约束系统的不带乘子的Lagrange方程。完整约束系统与非完整约束系统具有如下区别:
1)对于完整约束系统,在引进新的位移参数后,所有的广义坐标都是新参数的函数;对于非完整约束系统,在引进新的位移参数后,所有的广义坐标不仅是新参数的函数,而且与新参数的导数有关,还含有积分。
2)对于完整约束系统在解除约束后,系统的Lagrange函数只与新参数及其一阶导数有关;对于非完整约束系统的Lagrange函数与新参数以及它们的一阶导数和二阶导数有关,并且还含有积分。
3)完整约束系统与非完整约束系统运动方程的形式不同。
[1] GOLDSTEIN H. Classical Mechanics[M]. [S. l.]:Addison-Wesley Pub. Co.,1980:1-50.
[2] 黄文虎,陈 滨,王照林. 一般力学(动力学、振动与控制)最新进展[M]. 北京:科学出版社,1994:37-45.HUANG Wenhu,CHEN Bin,WANG Zhaolin. Recent Advances in General Mechanics (Dynamics, Vibration and Control)[M]. Beijing:Science Press,1994:37-45.
[3] 梅风翔. 非完整系统力学基础[M]. 北京:北京工业学院出版社,1985:1-42.MEI Fengxiang. An Introduction to Nonholonomic Dynamics[M]. Beijing:Beijing University of Technology Press,1985:1-42.
[4] ARNOL’D V I,NOVIKOV S P. Dynamical Systems III[M]. Berlin:Springer-Verlag,1985:156-158.
[5] PIRONNEAU Y. Deplacements Virtuels Travail Nul,Conditions de Chetaev[C]//IUTAM-ISIMM Symposium on Modern Developments in Analytical Mechanics.Torino:[s. n.],1983:671-686.
[6] 郭仲衡,高普云. 关于经典非完整力学[J]. 力学学报,1990,22(2):185-190.GUO Zhongheng,GAO Puyun. On the Classic Nonholonomic Dynamics[J]. Acta Mechanica Sinica,1990,22(2):185-190.
[7] 郭仲衡,高普云. 再关于经典非完整力学:答《争议》[J]. 力学学报 , 1992,24(2):253-257.GUO Zhongheng,GAO Puyun. Futher Remarks on the Nonholonomic Dynamics[J]. Acta Mechanica Sinica,1992,24(2):253-257.
[8] 高普云,郭仲衡. 一类非完整力学系统的Lagrange方程[J]. 应用数学和力学,1991,12(5):397-400.GAO Puyun,GUO Zhongheng. Lagrange Equation of Class of Nonholonomic Systems[J]. Applied Mathematics and Mechanics,1991,12(5):397-400.
[9] 高普云,郭仲衡. 另一类非完整力学系统的Lagrange方程[J]. 应用数学和力学,1991,12(8):679-684.GAO Puyun,GUO Zhongheng. Lagrange Equation of Another Class of Nonholonomic Systems[J]. Applied Mathematics and Mechanics,1991,12(8):679-684.
[10] GAO Puyun. To Derive Lagrange Equation of Nonholonomic Systems Without Using the Chetaev Conditions[J]. Mechanics Research Communication,2005,32(2):255-264.
[11] JU I N,FUFAEV N A. Dynamics of Nonholonomic Systems[M]. Rhode Island:American Mathematical Society Providence,1972:99-106.
Derivation of Lagrange Equations of the First-Order Nonholonomic System Based on the Principle of Removal of Constraint
GAO Puyun
(School of Aerospace Science,National University of Defense Technology,Changsha 410073,China)
Based on the principle of removal of constraint, a motion equation of the first-order nonholonomic constraint system has been derived from the d'Alambert principle. By introducing new displacement parameters, the fi rst-order nonholonomic constraints are lifted, thus making the nonholonomic system an unconstrained system, with the new Lagrange equations successfully derived without multipliers.
lifting of constraints;nonholonomic system;Lagrange equation;displacement parameter;unconstrained system
O313.3
A
1673-9833(2017)05-0001-05
10.3969/j.issn.1673-9833.2017.05.001
2017-08-19
高普云(1962-),男,湖南攸县人,国防科技大学教授,博士生导师,主要从事动力学与控制方面的教学与研究,E-mail:gfkdgpy@hotmail.com
(责任编辑:邓光辉)

