雷达对抗并行仿真的负载优化分析*
于 尧, 赵忠文, 郭皇皇
(装备学院复杂电子系统仿真实验室, 北京 101416)
雷达对抗并行仿真的负载优化分析*
于 尧, 赵忠文, 郭皇皇
(装备学院复杂电子系统仿真实验室, 北京 101416)
针对雷达对抗并行仿真中存在状态通信较大和计算负载不易平衡的问题,提出了简化“负载优化问题”的方法。将模型的通信问题转化为模型交互作用问题,通过静态分析方法,从时间、概率、数量三个方面计算模型间的交互作用,将模型的计算负载转化为模型复杂度问题;通过群决策法分析计算模型复杂度。并利用区间理论对群决策法进行改进,减少了决策信息的主观性、剔除了区间内的不一致信息。仿真数据表明,通过这种简化“负载优化”的方法能够合理将模型映射到处理器上,并能较好地实现仿真的并行,效率的大幅度提高验证了该方法的有效性。
负载优化; 静态分析; 群决策; 雷达对抗; 并行仿真
为了充分发掘雷达对抗的并行潜力,负载优化是提高并行仿真效率的关键[1],其主要研究如何利用先验知识将n个模型分配到m个处理单元,才能既减少模型之间的消息传递开销,又充分发挥各处理单元的处理能力,即通信负载问题和计算负载问题。其一般解决方式分为动态负载平衡以及静态负载平衡两种算法,文献[2-3]提出了启发式算法的任务调度方法,减少负载迁移次数,文献[4]根据兴趣域的算法解决了负载迁移过程中出现的不平衡问题,文献[5-7]根据Min-Min调度算法,将重负载资源的任务分配给轻负载资源执行。这些算法都属于动态负载平衡,它是一种通用的平衡方法,由于动态平衡本身存在开销很大的问题,尤其在大规模交互仿真中尤为明显,不适合雷达对抗仿真大规模事件交互的特点。在静态负载平衡技术中,文献[8-12]针对不同场景采用启发式算法进行静态分析以提高资源利用率。刘鑫等人提出规则分块算法和不规则分块算法相结合的方法,从图论的角度讨论了静态负载平衡问题[13]。但国内文献中对于雷达对抗的静态分析研究的相对较少,因此本文针对雷达对抗的负载优化问题采取静态分析的方法进行研究。
在大规模的模型仿真中,模型间的复杂交互使得通信负载和计算负载的测试及优化变得繁琐及困难,因此本文将这个复杂问题进行了转化,将模型的通信转化为模型的交互作用,以关系距离进行表示,将计算负载转化为模型的复杂度,以模型复杂度权重值表示。交互作用是从时间、概率、数量三个方面进行静态分析,目的将交互频繁大的模型聚合到统一处理器以减少状态通信,模型复杂度采用群决策法计算,并利用区间理论对其进行改进,减少了信息的主观性,并剔除了区间内的不一致信息,并根据交互作用对模型复杂度进行修正,目的让每个处理器聚合的模型复杂度相差较小,以充分发挥处理器性能。
1 负载优化问题简化
仿真模型如何映射到并行处理系统更高效,涉及负载优化的问题。由于同一个处理器上模型的通信开销将远小于不同处理器的通信开销,因此应当将存在较大通信量的仿真模型指派到同一个处理器上,以减少通信负载,为充分发挥多核处理器计算能力,每个处理器应根据自身处理能力以及模型计算量进行适度映射。
由于模型间的通信量以及模型计算量在整个动态仿真中是变化的而且难以准确测量或描述,因此可将该问题简化,将模型的通信问题转化为模型交互作用问题,将模型的计算问题转化为模型复杂度问题。模型的交互作用体现在传递消息上,传递消息越频繁,交互作用就越大,两个模型间的通信越就紧密,将交互作用频繁的模型聚合在同一个处理器上,将会减少通信开销。模型复杂度体现在模型设计及程序设计上,采用群决策法对模型复杂度进行比较分析,然后根据层次分析法可计算出各模型复杂程度的权重,该权重值即为模型复杂度。为了降低决策打分的难度,打分时并不需要根据实际仿真任务场景进行判断,仅根据模型的相互触发关系、模型的内部设计结构、以及模型程序设计的复杂程度进行判断打分。但实际中模型的计算量不仅和模型的复杂度有关,还与模型在仿真中执行的次数有关,因此可通过交互作用进行补偿修正。最后将交互作用频繁的模型聚合在一起,映射到同一个处理器上以减少通信开销,使每个处理器聚合后的模型复杂度相差较小以充分发挥多核处理器计算性能,从而实现通信负载和计算负载的优化。
2 模型交互作用静态分析
静态分析方法是围绕特定仿真任务进行分析的一种方法,静态是指只在仿真运行前进行处理器映射,在仿真运行的过程中不作调整,直到仿真运行结束为止。通过将仿真任务合理映射到处理器,达到仿真系统的综合性能最优。
在雷达对抗仿真中,模型交互作用的静态分析的整体思想是:将仿真任务划分为若干子任务,并分析每个子任务的模型交互,每个子任务由相应的仿真模型交互组成。在确定子任务的静态分析图后,计算每个子任务初始两个模型的交互作用,然后根据每个模型的触发概率,按照循环结构的顺序计算两两模型间的交互作用。雷达对抗仿真的静态分析可分为以下四个步骤:
1)分析子任务的模型交互关系
将仿真任务拆分成若干个子任务,并分析每一个子任务中模型的交互关系。每个子任务是由雷达对抗的功能模型构成的循环结构,该结构周而复始的执行,直到某个模型由于其他模型作用而打破循环致使仿真结束。以导弹突防中的交互为例,整个任务中可以分成雷达干扰导弹与导弹袭击目标两个子任务,每个子任务为一个循环结构。在前一个子任务中,导弹可由控制实体位置及路线的运动模型代替,导弹的运动模型将导弹位置信息报告给敌方雷达的侦察模型,侦察模型探测到导弹触发雷达的决策模型,决策模型将目标信息进行威胁比对识别,把决定的干扰方式发送给干扰模型,干扰模型按照干扰方式对导弹的运动模型实施干扰,若途中导弹被干扰成功,导弹的运动模型失效,退出循环结构,否则发送位置更新事件,再次执行运动模型,继续执行循环结构。在后一个子任务中,在导弹飞行到目标过程中,导弹不断检测与目标的位置,若导弹位置达到袭击目标的位置时,即导弹命中,导弹的运动模型失效,退出循环结构,否则运动模型将向自身报告位置更新事件,继续执行循环结构。导弹突防模型间交互如图1所示,图中粗线体现的就是模型间的交互作用。
2)静态分析图确定
静态分析图是静态分析的前提条件,它反映了运动目标可能发生交互的位置,并对该位置进行标定。需要注意的是,静态分析图并非是实际仿真中的某一时刻的准确仿真图,而是每个子任务中运动目标第一次发生交互的瞬间静态的图,模型第一次发生交互的初始位置称为交互初始点。
在雷达对抗中,所有的研究是围绕侦察、干扰两个功能展开的,两者的范围可简化为以装备实体为圆心,模型作用距离为半径圆,目标的运动可简化为匀速直线飞行,因此位置的标定可以用圆和直线的交点进行表示。例如,侦察模型的范围可看作是一个以雷达为圆心,雷达探测距离为半径的圆,当发生压制作用时,该半径为压制后的探测距离;干扰模型的作用范围可看成是以干扰机为圆心,干扰距离为半径的圆;目标实体第一次进入最近的圆的范围,成为为交互初始点,如图2所示,d1为目标第一次发生交互的位置,即交互初始点,R1、R2、R3为雷达装备实体,每个实体含有侦察模型、决策模型以及干扰模型。
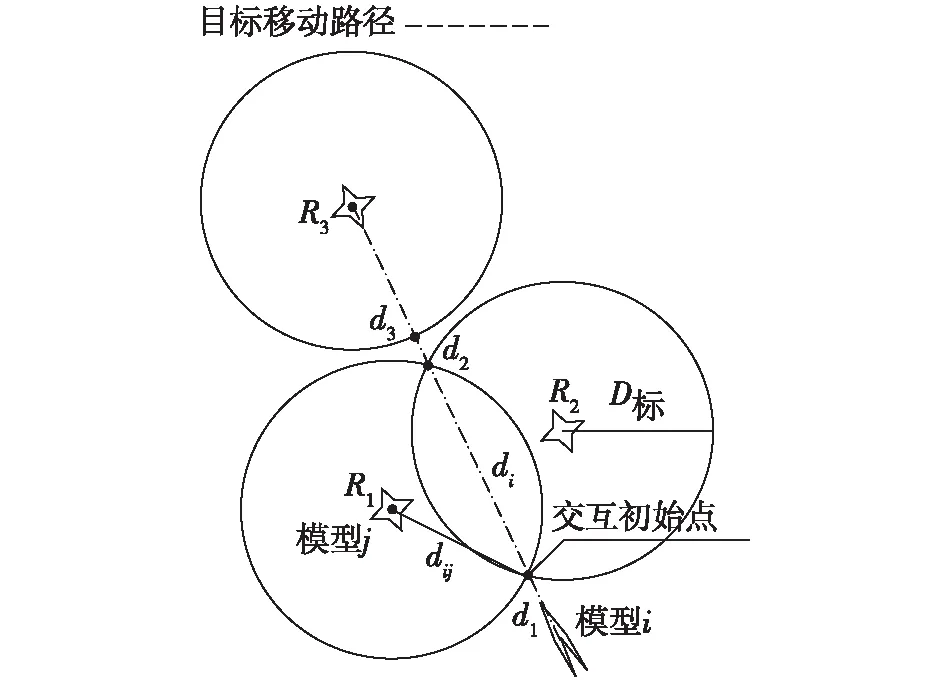
图2 模型的静态分析示意图
3)交互作用的静态分析计算
在雷达对抗中,实体装备的交互作用一般与时间、概率、数量三个因素相关,在双方交互的区域内运行的时间越长,双方发生交互作用的次数也就越多,因此需要考虑时间因素;双发交互的区域内,模型的交互存在作用概率,作用概率越大越可能造成某一方或两方的失效,从而交互作用的次数将减少,因此需要考虑概率因素;在仿真中可能需要一组某型号的装备执行任务,由于该类装备的模型及参数均相同,因此可将一组的实体装备用一个实体的模型表示,然后对整个循环中涉及的交互作用进行数量因素修正。各因素及交互作用的计算方法如下:
①时间因素的计算
雷达对抗的模型交互如果涉及距离和速度的概念,则需要进行时间修正。在雷达对抗中,正是由于运动的实体进入另一个实体的作用范围才发生了模型的交互循环结构,这里需要假设实体间的交互作用不会使得交互双方的实体模型发生失效的情况,因此时间因素系数计算如式(1)所示,其中di、vi分别为运动模型在探测范围(或干扰范围)的目标运动距离和速度,(d/v)max为整个仿真中di/vi的最大值,dij为模型i与模型j的相对距离,D标为(侦察或干扰)模型的标称距离,如图2所示。
(1)
②概率因素的计算
而实际仿真中,时间因素的假设是不准确的,模型可能因为实体作用而失效,运动目标只是有一定概率完成整段行程,因此交互模型需要考虑概率因素,该概率的意义应是整段行程不失效的概率,如式(2)所示,p失为该模型失效的概率,失效概率的计算可以按照交互作用关系层层计算,以图1的交互作用关系为例,对于运动模型来说p失=p探测·p识别·p干扰,p探测为侦察模型的探测概率,p识别为决策模型的识别概率,p干扰为干扰模型的干扰概率。概率因素的实质是维持各个模型不失效的概率,模型不发生失效则模型间的交互作用保持不变。
p=1-p失
(2)
但如果多个雷达探测目标存在次序和作用重叠等问题时,p失需要根据条件概率及循环结构中的模型概率进行估算。如图2所示,雷达R1,R2对导弹di的探测存在交互重叠,R1、R2、R3均为参数相同的雷达,雷达具有侦察模型、决策模型和干扰模型,p探测为0.6,p识别=1,p干扰=0.7,目标经过d3R2之前经过了d1d2,存在次序关系以及R1、R2作用重叠问题,因此计算导弹与雷达R3的失效概率需要先估计d1d2段的导弹未失效的概率,d1d2段发现目标概率易知为0.84,目标在d1d2段干扰失效概率0.84*0.7=0.588,目标能经过d3R2的概率为1-0.588=0.412,因此运动目标与R1、R2的侦察模型的概率因素系数为1-0.6*1*0.7=0.58,与R2侦察模型的概率因素系数为0.412*(1-0.6*1*0.7)=0.238。
③数量因素的计算
在仿真中可能需要多组某型号的装备执行任务,每组有某实体装备若干,由于该类装备的模型及参数均相同,可将一组装备用组成该装备的一组模型来表示,然后进行数量修正,数量因素s即为每组的实际数量。
④交互作用的计算
每一个子任务可看成是一个循环结构,在循环过程中我们认为这种交互作用是可以传递的。例如虽然运动模型与决策模型没有交互,但若增加运动模型数量,直接反映是侦察模型更频繁触发,引起其与侦察模型的交互作用增加,从而使得侦察模型与决策模型的交互作用增加,这种交互作用的增加可以认为是侦察模型交互作用的间接反映。但传递的交互作用不是等幅度增加的,因为每传递到一个模型后,该模型是按照一定概率才会触发下一个模型,这个触发是有条件的,我们将这个条件的实现概率称为触发概率,在雷达对抗中该概率往往就是模型的作用概率。如图2所示,侦察模型触发决策模型的触发概率即为侦察模型的探测概率,决策模型触发干扰模型即为决策模型的识别概率。

(3)
为了将交互频繁的模型映射到相同的处理器,可将模型间的交互作用转化为关系距离的概念,交互作用越大,两者的关系距离则越小。按照关系距离对模型进行聚合,交互作用转化为距离的计算如式(4)所示,其中dijnew表示关系距离。
(4)
4)基于蚁群算法的模型聚类
根据各模型之间的关联距离,采用蚁群算法将各模型连接为一个总关联距离最小的封闭图形。然后按照关联距离由大到小的顺序依次断开,直到发生断开边的模型存在紧密的交互作用后停止(设置关联距离小于某一阈值即停止),我们可认为剩余连接的模型都是交互频繁的,按照连接的模型进行聚类。蚁群算法分类问题具体可参考文献[1]。
3 基于改进群决策法的模型复杂度计算
群决策也称为多人决策,它是将不同知识结构和不同经验的决策者集中在一起,弥补个人知识及经验不足的科学决策方法。在一个群决策过程中,大多要求各个决策者给出因素的评价分值或是比较的结果等。
模型复杂度反映了模型的计算量,模型越复杂,计算量也将越大,决策者根据模型的相互触发关系、模型的内部设计结构,以及模型程序设计结构进行比较判断,然后根据层次分析法计算各模型复杂程度权重值,将其作为模型复杂度的值,但模型的计算量除了与模型的复杂度有关,还与模型的交互次数相关。例如一个模型的复杂度为100,但是在仿真中只进行了一次计算就结束了,而另一个模型复杂度虽然只有30,却计算了10次,模型复杂度低的却有更高的计算量,对此我们还需根据静态分析得到的交互作用对模型复杂度进行修正。
在实际的群决策过程中,由于受到决策者知识结构、判断水平和个人偏好等众多主观因素的影响,再加之判断事物本身的模糊性和不确定性,决策者们即使针对同一问题的判断也将会存在个人的主观偏好,使得结果相差较大,信息难以一致的融合。因此将区间理论分别引入群决策法中,并在决策者的区间打分中引入了决策者的理想值,根据欧氏距离的思想,得出决策打分的差异度,对决策打分信息的置信度进行修正,由于区间内不存在不一致信息,采用区间弱一致性理论剔除不一致性信息,并根据等比的思想映射出修正后区间的理想值,形成的理想值矩阵更能柔性地反映决策者的偏好,使信息更易于满足一致性并更容易被决策者所接受。其步骤如下:
1)区间关系矩阵和判断矩阵的打分
决策者在进行指标两两比较时,打分结果不仅要给出区间,还要给出最可能的值作为理想值,即形如(ai-,ai,ai+)其中ai-,与ai+为区间的两端,ai为决策者i认为的理想值,收集所有信息。其模型复杂度比较的评语集应为表1所示。

表1 模型i对模型j复杂度的评语集
注:决策打分以提供的上述标准为参考,给出一个区间,并给出该区间内最可能的值作为理想值。
2)指标融合权重的计算
①差异度计算
对于调查中的“指标m1比m2重要”,不同决策者对此的打分可能不同,我们需要知道决策者判断差异的大小进行得分融合,进而形成最终的关系矩阵或判断矩阵。由于欧氏距离能够体现个体数值特征的绝对差异,能够从数值的大小中体现差异,所以决策者判断的差异性我们采用欧氏距离度量的方法计算。其公式为

(5)

②置信度计算
假定有n位决策者参与决策,形成的n个判断矩阵,根据信息的置信度对n个判断矩阵中的每项两两打分进行融合,我们认为打分差异大的信息相对置信度较低,差异小的置信度相对较高,对于“指标m1比m2重要”,决策者i和决策者j相似度公式为
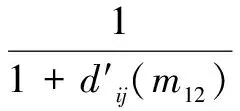
(6)
令
(7)
式(7)中的si(m12)反映了决策者i(i=1,2,3,…,n)与其他决策者对该项比较打分的相似程度之和。对于“指标m1比m2重要”决策者i的置信度为
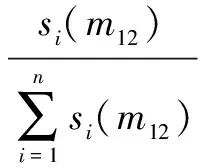
(8)
3)判断矩阵的区间进行弱一致性检验
上述融合方法是根据决策者间的差异性进行融合,由于这样融合后的判断矩阵内存在不一致信息,区间内含有不一致信息的区间判断矩阵称为弱一致区间判断矩阵,为避免不一致信息对评估的影响,需要进行弱一致性检验消除不一致信息。
设A=(Aij)n×n为弱一致区间判断矩阵,根据区间理论可得
(9)
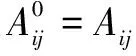
由式(9)可以计算出第一次进行弱一致检验后的区间如式(10)所示

(10)

4)建立理想值判断矩阵
决策打分的理想值在区间的位置,反映了该理想值在区间的可能性大小,因此根据等比映射的原则,可将理想值修正为
(11)
将式(11)计算的理想值从区间判断矩阵中提出,形成理想值判断矩阵。
5)模型复杂度的计算
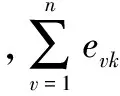
(12)
按照上文的蚁群算法得到的几组聚类的模型,分别计算每组模型总复杂度,分别将各组模型映射到处理器上,并保证分组后的每组模型的模型总复杂度相差不大,即完成了负载优化的工作。
4 实验结果分析
现对敌方分布的5个目标群进行地面目标进行导弹袭击,每个目标群都配有一组固定的雷达及干扰设备,其坐标分别为(4800,9600)、(8400,11400)、(10800,12600)、(7800,15000)、(4800,13200),分别采用128/256/314/512/640枚导弹进行目标群轰炸,导弹分配到五个目标群数量比为26:26:26:25:25,我方基地坐标为(14700,1800),雷达探测标称距离及干扰作用的标称距离为2400m,探测概率为0.6,识别导弹信息概率为0.8,干扰概率为0.8,总共的干扰资源为640个,导弹的速度为900m/s,如图3所示。

图3 导弹突防仿真静态分析图
1)模型交互作用的静态分析
实验算例采用的是导弹突防仿真问题,其功能模型的交互如图1所示,可以将仿真按照静态分析图分成5个子任务,即图3的五条路线,现对子任务D5袭击R5目标群,与R5的三个模型的交互作用进行计算。其中D5与R2的t=(d1d2/v)/(d4d7/v)=0.87,p=1-0.6*0.8*0.8=0.62,s=25,D5的运动模型对R2的侦察模型的交互作用为t*p*s=13.43,2的侦察模型与决策模型的交互作用为13.43*P侦察=8.06,其余交互作用计算按照式(1)、(2)计算以此类推,计算结果如表2所示。
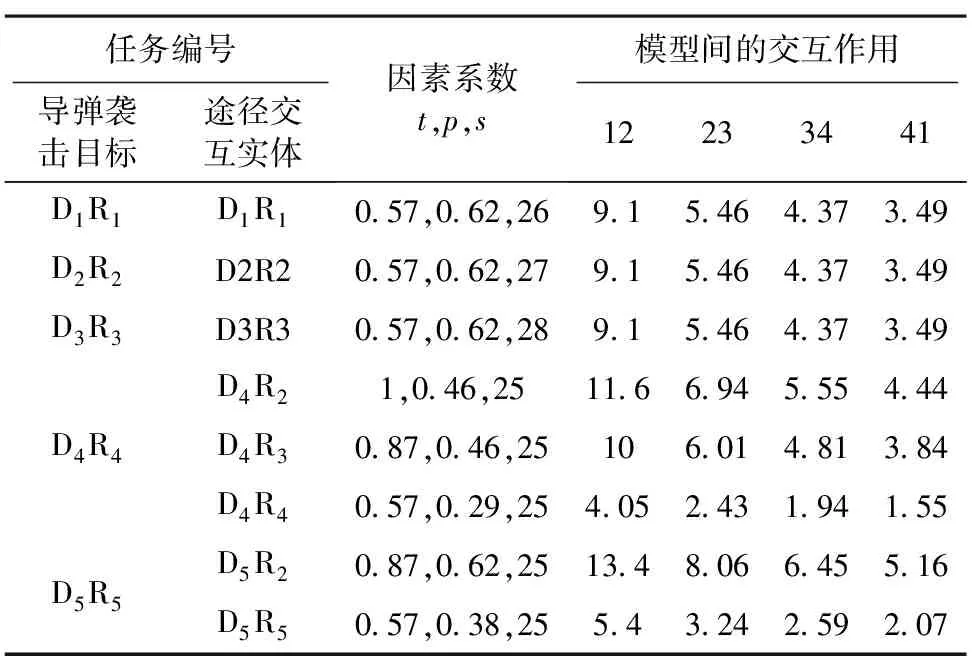
表2 模型间的交互作用
注:表中模型间的交互作用12、23、34、41分别代表不同模型的交互作用,1代表侦察模型,2代表决策模型,3代表干扰模型,4代表运动模型。
根据距离将模型进行聚合,具体聚合的方法可采用启发式算法,本文不做详细阐述,具体可参考文献[1]可将模型聚类如图4所示,其中数字分别按照D1-D5的运动模型、R1-R5的侦察、决策、干扰模型3个模型为序。
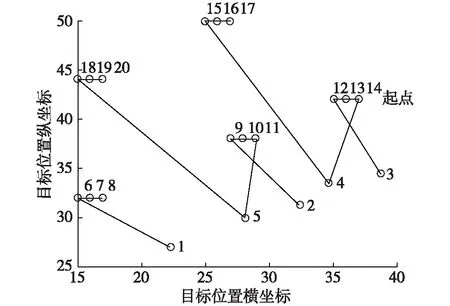
图4 模型交互作用的聚合图
2)模型复杂度的计算
决策者根据仿真模型的交互以及模型的结构设计对判断矩阵进行打分,并对判断矩阵进行修正,根据得到的理想值判断矩阵和AHP法求得4个模型复杂度分别为0.53、0.11、0.08、0.29。聚合后模型进行交互作用补偿后,可得聚合后单位模型复杂度,以20/19/18/5/11/10/9/2段为例,是由25枚导弹D5和26枚导弹D2组成的,因此可将其拆分为25个3/12/13/14/4/15/16/17和1个3/12/13/14,其单位复杂度分别为0.94和0.362,同理20/19/18/5/11/10/9/2拆分为25个20/19/18/5/11/10/9/2和1个11/10/9/2,其单位复杂度分别为1.14和0.362。然后根据每个处理器的模型复杂度平衡原则将模型映射到处理器上。映射到四核和八核处理器上
3)仿真实验验证
基于ROSS仿真引擎对上述模型进行实现,将模型分别映射到处理器为四、八核的处理器上进行运行,并与串行仿真进行比较,比较结果如图5所示,经比较发现并行仿真中,四核处理器仿真效率比串行提高63.0%,八核处理器仿真效率比串行提高73.6%,均能够较好地发挥并行仿真的能力,验证了该静态分析方法将雷达对抗模型映射到处理器的有效性,能够比较充分发挥多核处理器的性能。
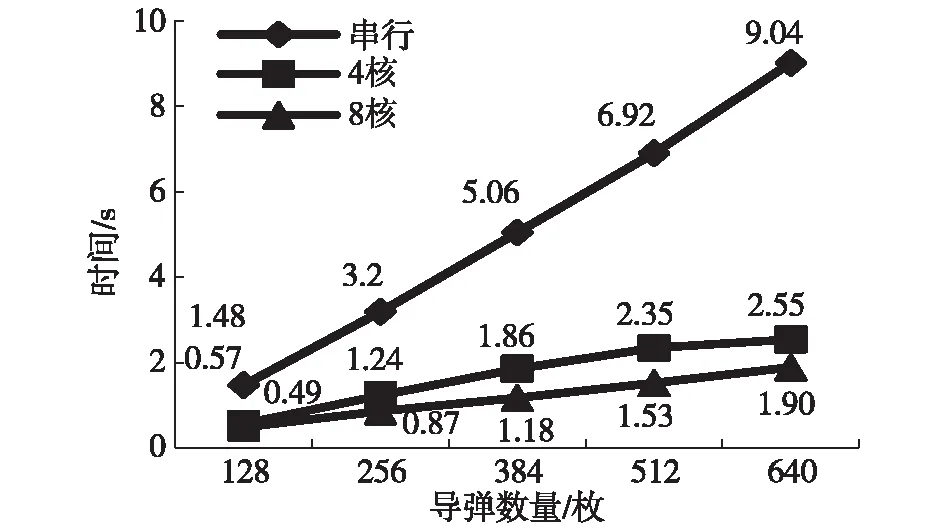
图5 并行仿真与串行仿真的效率对比
5 结束语
本文将仿真模型通信负载及计算负载问题简化为模型交互作用及模型复杂度问题,根据静态分析和改进的群决策法对两者进行分析计算。仿真结果表明这种简化“负载优化问题”的方法的有效性,能够比较充分发挥处理器性能,为雷达对抗并行仿真的负载分析提供了新思路。
[1] 朱广蔚, 秦小麟, 许峰. 一种基于负载均衡的多Agent路径规划算法[J]. 南京航空航天大学学报, 2010, 42(2):198-203.
[2] 张颖星, 姚益平. 乐观策略下并行离散事件仿真动态负载划分优化算法[J]. 计算机学报, 2010, 33(5):813-821.
[3] 曾蛟龙, 胡荣贵, 黄海军,等. 基于最小通信开销的动态负载均衡策略[J]. 计算机工程与应用, 2013, 49(17):103-107.
[4] Alkharboush R, Grande R E D, Boukerche A. Load prediction in HLA-Based Distributed simacation osing Holt’s variaants[C]∥International symposium on Distributed simulation and Real Time Applications. IEEE computer society,2013:161-168.
[5] Wang W, Yan Y, Zhou J. Optimization of Min-Min task scheduling algorithm based on load balance[J]. Journal of Nanjing University of Science & Technology, 2015, 39(4):398-404.
[6] 张忠平, 温利娟. OPT-Min-Min:基于Min-Min网格资源调度算法的优化[J]. 小型微型计算机系统, 2014, 35(7):1573-1577.
[7] 蔡国强, 贾利民, 邢宗义,等. 基于蚁群算法的模糊分类系统设计[J]. 模糊系统与数学, 2008, 22(4):87-98.
[8] 彭艳飞, 王正友, 周代利,等. 基于蚁群算法的网格任务调度模拟[J]. 矿山机械, 2008,36(4):49-52.
[9] 李静梅, 张大虎, 吴艳霞,等. 基于蚁群优化算法的异构多核线程调度方法[J]. 计算机工程与设计, 2014, 35(6):1946-1950.
[10] 范绍聪, 刘怡俊. 基于量子蚁群算法的片上网络映射研究[J]. 计算机应用研究, 2017, 34(1):156-159.
[11] 刘进, 刘春, 陈家佳. 基于改进蚁群算法的多处理器任务调度仿真[J]. 计算机仿真, 2014, 31(6):334-337.
[12] Zhu L, Tang R, Tao Y, et al. Multi-objective Ant Colony Optimization Algorithm Based on Load Balance[J]. Cloud computing and secruity,2016.
[13] 刘鑫, 陆林生. 数据不规则问题并行计算的负载平衡策略的研究[J]. 计算机应用, 2004, 24(10):108-111.
[14] 韦兰用.弱一致区间数判断矩阵的一致性逼近[J],广西工学院学报,2003,14(1):15-17.
Load Optimization Analysis of Radar Countermeasure Parallel Simulation
YU Yao, ZHAO Zhong-wen, GUO Huang-huang
(Science and Technology on Complex Electronic System Simulation Laboratory, Academy of Equipment, Beijing 101416, China)
In allusion to the problem that the state communication is frequent and the calculation load is not easy to be balanced in the radar countermeasure simulation, a method of simplifying the "load optimization" is proposed. The communication problem of the model is transformed into the model interaction problem, through the static analysis method, the interaction between the models is calculated from the three aspects of time, probability and quantity. The calculation load of the model is transformed into the model complexity analyzed by the group decision method. The group decision method is improved by the interval theory, which reduces the subjectivity of decision information and eliminates inconsistent information in interval. The simulation data shows that this simplified method of "load optimization" can reasonably map the model to the processor and demonstrates the effectiveness of the method.
load optimization; group decision method; radar countermeasure; parallel simulation
1673-3819(2017)06-0089-07
TN974;E917
A
10.3969/j.issn.1673-3819.2017.06.019
2017-07-29
2017-09-13
国防预研基金项目
于 尧(1992-),男,辽宁瓦房店人,硕士研究生,研究方向为信息系统技术与应用。赵忠文(1974-),男,硕士,副研究员。郭皇皇(1993-),男,硕士研究生。

