基于复杂网络的动态天基预警系统抗毁性测度及影响因素灰色关联分析*
杨苗本, 熊 伟
(航天工程大学, 北京 101416)
基于复杂网络的动态天基预警系统抗毁性测度及影响因素灰色关联分析*
杨苗本, 熊 伟
(航天工程大学, 北京 101416)
针对天基预警系统的抗毁性问题,提出了系统网络连通熵抗毁性测度模型,分析了天基预警系统抗毁性整体、动态、对抗的变化情况。构建了由网络的平均度、平均路径长度、聚类系数、网络直径、网络全局效率和最大连通子图等组成的影响因素指标体系并进行了灰色关联分析,量化了系统网络抗毁性与主要因素之间的关联度。最后结合算例总结了各个因素对天基预警系统抗毁性的影响能力。
复杂网络; 天基预警系统; 网络连通熵; 动态; 抗毁性; 灰色关联分析
天基预警系统能够为军方作战提供战略预警、战勤保障、信息支援等,在国防和反导体系作战中有着不可替代的地位。目前我国天基预警系统建设还在起步阶段。天基预警系统包含的卫星众多,所承担的任务也很复杂。这些数目众多的卫星作为一个整体,相互之间通过星间/星地链路构成一个复杂网络,以满足多样化的使命任务需求。因此,通过对天基预警系统网络结构及特性的深入分析,可实现对天基预警系统的结构优化和抗毁性分析[1]。
天基预警系统抗毁性是指系统网络的拓扑结构在遭到蓄意或者随机破坏之后,能够持续提供服务、继续发挥其性能和效能的能力,也叫系统网络的抗攻击性。对于天基预警系统而言,其抗毁性研究对于在恶劣环境下获取预警信息、抵御敌方导弹攻击、正常发挥作用有重要意义。因此,这就要求对天基预警系统的抗毁性有更深入的理解,以便于控制网络故障的发生,保证系统网络的正常运行。因此,抗毁性测度作为系统网络的本身属性,研究抗毁性效能与其影响因素之间的关联关系十分必要。影响天基预警系统抗毁性的因素是多方面的,主要有网络的平均度、平均路径长度、聚类系数、网络直径、网络全局效率、最大连通子图等。通过对天基预警系统抗毁性及影响的深入分析,既可得到对于抗毁性影响较大的因素,也可在分析对比中优化系统网络的拓扑结构,提高系统自身的顽存能力,这对于发展天基预警系统、调整战略预警力量配置等具有较强的理论及现实意义[2]。
1 天基预警系统的复杂网络特性分析
1.1 天基预警系统
天基预警系统可近实时地监视弹道导弹等目标的发射,通过对目标的跟踪、分析和拦截等来完成预警任务。天基预警系统的卫星星座主要由2部分组成:天基预警系统高轨部分和天基预警系统低轨部分。其中:高轨部分由若干颗地球静止轨道卫星和大椭圆轨道卫星构成,这些地球静止轨道卫星和大椭圆轨道卫星可实现对全球位置的覆盖;天基预警系统低轨部分由飞行在若干个轨道面上的数十颗低轨道卫星组成。高轨卫星除了起到探测作用之外,还可部分代替中继卫星的功能,低轨卫星探测到的信息可通过高轨卫星传送到地面站。图1是运用STK软件仿真出的天基预警系统某一时刻的物理模型[3]。
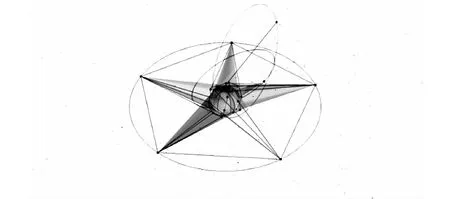
图1 天基预警系统物理模型图
高轨预警卫星通过红外探测器探测到发射导弹尾焰的红外信息后,通过与地面站之间的星地链路将目标信息传送到地面站。地面站对信息进行初步分析后向地面指控中心汇报。指控中心迅速对目标的发射地点、轨道参数以及攻击目标做出分析和判断后对相应地区的低轨卫星发出指令。收到指令之后,低轨预警卫星对导弹目标进行跟踪探测,并将获取到的跟踪信息通过中继卫星(其功能可由高轨卫星代替)传送到地面接收站。最后,在天基信息支援和上级指令下,对敌方来袭导弹进行拦截[4]。
1.2 复杂网络
复杂网络是由大量节点和这些节点的连边组成的。其中,节点代表真实系统中不同的个体,而边则表示个体间的关联。即2个节点之间具有某种特定的关系则连一条边,反之则不连边。构建复杂网络的本质是把天基预警系统抽象成若干节点和边。例如,将天基预警系统的卫星和用户抽象成相应的节点,系统中的信息交互关系抽象成相应的边,那么由节点和边构成的一个集合就是一个完整的拓扑图,可运用拓扑学的相关知识对其进行研究和计算。具体实现过程如下:定义G(V,E)一个无向网络。其中:V是节点的集合,E为边的集合;网络中节点总数为N[5]。图2是利用Gephi软件构建出的系统网络的拓扑结构图[6-7]。
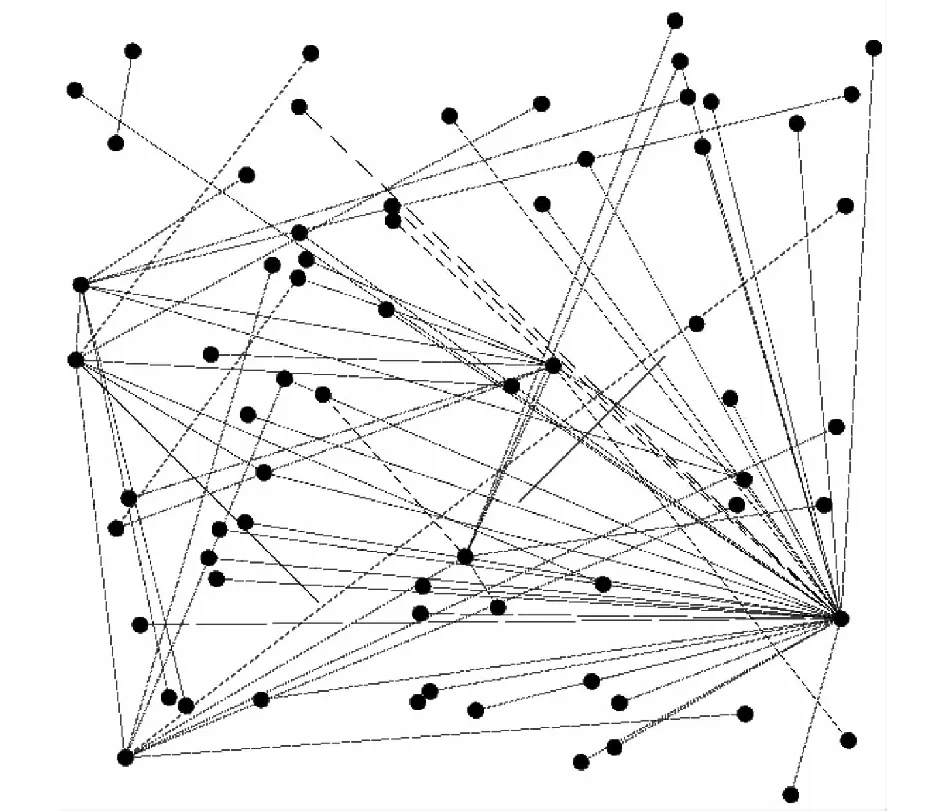
图2 天基预警系统复杂网络拓扑结构图
2 基于系统网络连通熵的动态抗毁性测度分析
2.1 基于节点价值和熵的抗毁性测度方法
抗毁性是一个复杂的系统问题,需要运用指标来综合衡量一个系统或者网络的抗毁性能力。衡量过程中,网络的拓扑结构甚至每一个节点、链路的属性都会影响到最终的衡量结果。在这个层面上,研究天基预警系统要将抗毁性与系统网络整体的拓扑结构和属性结合起来,借鉴目前复杂网络抗毁性测度方法中的熵模型,结合节点的结构价值属性和信息价值属性,研究天基预警系统动态网络的抗毁性效能,并构建出相应的抗毁性测度评价指标[8]。
1) 系统网络连通熵抗毁性测度分析方法
熵在物理学上被用以描述热量转化为功的程度,在科学技术上表征系统不确定的程度,而在传播学中表示一种情境的无序性和不确定性。基于节点价值的基础和熵的概念,笔者提出了适合天基预警系统的网络连通熵测度模型,即系统网络连通熵抗毁性测度模型。该模型是在网络节点结构层面和信息层面上衡量节点价值的基础上,结合熵的概念而提出的,用以反映网络中节点综合价值的分布情况,从而达到度量网络抗毁性的目的[9]。
定义图G的网络连通熵如下:
(1)
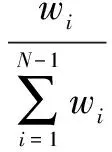

2) 节点价值度量方法
本文引入的系统网络连通熵抗毁性测度模型反映的是节点抗毁度分布的均匀性。它是在基于节点重要度研究的基础上,针对天基预警系统网络具有信息传输的特性,进一步将节点的结构价值和节点的信息价值进行加权,然后基于该综合价值指标构建熵模型,以评估天基预警系统网络在面对不同打击模式时的抗毁性。
节点结构价值的计算方法是基于节点收缩法,通过计算节点收缩前后网络的凝聚度来衡量节点的结构价值。该方法认为,收缩之后的网络凝聚度越大,该节点就越重要[10]。
假设vi是图G=(V,E)中的一个节点,可用G*vi表示将节点vi收缩后得到的图。所谓将节点vi收缩是指将与vi相连的ki个节点都与vi融合,即用一个新节点代替这ki+1个节点,原来与它们关联的边现在都与新节点关联。
以下称
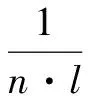
(2)
为图G的凝聚度。其中,n≥2,dij代表节点i与节点j之间的最短距离。当n=1时,令∂=1,显然0<∂≤1,当网络中只有一个节点时,∂取最大值为1。
以下称

(3)
为节点vi的结构价值。其中,G*vi表示节点vi收缩后所得到的图。
节点信息价值度量方法可用特征向量来衡量,特征向量指标强调节点之间的相互影响,节点的重要性不仅与其相连的边数有关,而且和与该节点连接节点的重要性呈线性关系。节点可通过连接重要的节点间接提升自己在网络中的重要性[11]。
设网络具有N个节点,A表示网络的邻接矩阵,λ1,λ2,,λN表示A的N个特征值,λ为矩阵A的最大特征值(主特征值),其对应的特征向量为e=[e1,e2,en]T,则有
(4)
则节点vi的特征向量指标可定义为
(5)
特征向量指标适合于描述节点的长期影响力,主要用于传播分析,如信息扩散等。在这些网络中,特征向量指标高的节点通常说明该节点距离信源很近,是需要重要防范的关键节点。
节点综合价值为节点结构价值与节点信息价值的加权求和值。其计算公式如下
wi=s1*IMC(vi)+s2*Ce(vi)
(6)
其中,wi表示节点在综合考虑结构层面和信息层面下计算所得的节点i的综合价值。s1与s2的值可根据任务的重要程度来进行定义。若任务的信息重要程度高,则定义节点的信息价值占比重高,即s2的值大;反之,则定义s1的值大。s1+s2=1,在具体计算时可取s1=s2=0.5。
2.2 天基预警系统复杂网络的算法性能
为了分析天基预警系统在对抗时的变化情况,运用两种不同的攻击方式(即蓄意攻击和随即攻击)对系统网络拓扑模型进行攻击,并将结果用图表的形式直观的呈现出两种攻击方式下运用网络连通熵计算得到的测度值变化情况。
图3和图4分别是天基预警系统在随机攻击和蓄意攻击下网络连通熵值的变化情况。分析可以看出,当s1和s2分别取不同值的时候,网络连通熵的变化趋势大致相同,并且s2的值即节点的信息价值所占的权重越大,连通熵的值也相对越大。

图3 随机攻击时S值不同三种情况下连通熵值
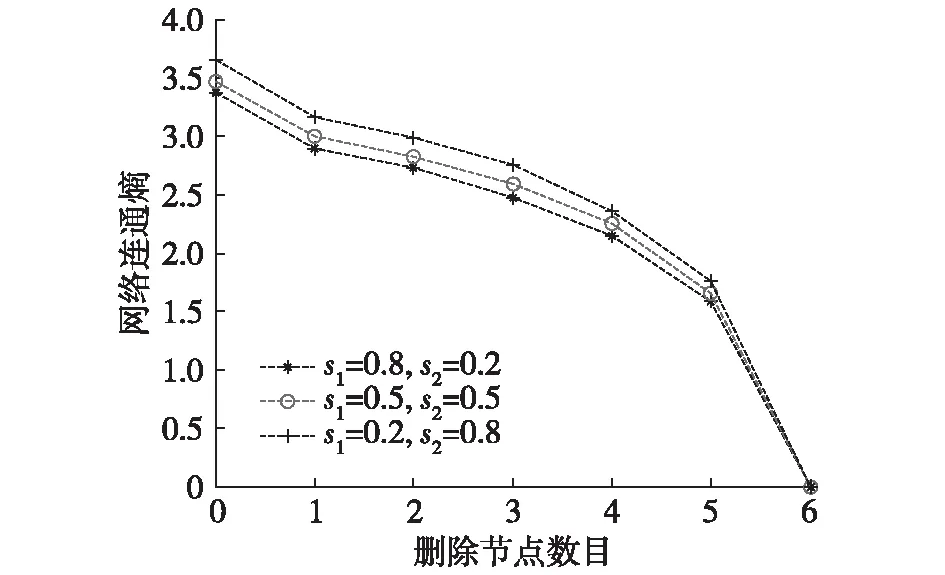
图4 蓄意攻击时S值不同三种情况下连通熵值
而且由于蓄意攻击的目标是系统网络中节点的度值最高的节点,因此这些节点遭受攻击后整个天基预警系统的网络拓扑结构发生重大改变,连通性和抗毁性都会发生很大变化,产生很多孤立节点,直至网络崩溃,丧失功能。
3 天基预警系统抗毁性影响因素指标体系构建及灰色关联分析
3.1 指标体系构建
抗毁性的计算结果属于不可控变量。为了对抗毁性变化的整体情况加以分析,需要找到影响抗毁性变化的可控变量。关于抗毁性影响因素评价指标体系,可从复杂网络基本静态特征指标和动态效能指标2个角度进行构建。这种指标体系构建有利于更全面地把握天基预警系统抗毁性整体、动态、对抗变化的影响因素。
在借鉴已有研究成果的基础上,充分考虑指标的获得性和代表性后,本文提出了6个影响因素并对其指标含义进行深入分析,即:网络的平均度

表1 天基预警系统网络抗毁性影响因素及具体含义
3.2 灰色关联分析
本文利用灰色关联分析方法对天基预警系统一段时间内抗毁性的效能指标及其影响能力进行分析。以便于动态分析抗毁性效能与复杂网络整体指标间的关联性。此方法可揭示抗毁性效能与系统网络指标之间的关联关系[12]。
由于自变量和因变量计量单位不同,不方便比较。因此在进行灰色关联分析之前,一般要进行数据的无量纲化处理。

(7)

然后计算相关系数,如x0(k)与xi(k)的关联系数:

(8)
其中,Δi(k)=|x0(k)-xi(k)|。ρ∈(0,),称为分辨系数,ρ越小,分辨力越大,一般ρ取值在(0,1)之间,具体取值视情况而定,通常取ρ=0.5。
最后计算关联度值,因为关联系数是为了量化数列与参考数列在各个不同时刻(即曲线中各点)的关联程度,因此要将各时刻(即曲线中的各点)所有关联系数求平均值,作为比较数列与参考数列之间的关联度。关联度ri公式如下:
(9)
其中,ri就是Xi(k)与X0(k)的关联度。关联度越大,则表示该因素对于系统抗毁性的影响也越大。
4 算例验证及分析
4.1 动态天基预警系统抗毁性测度
在构建与时间相关的复杂网络抗毁性测度模型的基础上,以下进行抗毁性效能随时间进行演化的相关分析。

表2 天基预警系统某日内抗毁性效能值
运用时间序列和统计分析的方法,将一组时间序列{t0,t1,t2,…Gtn}下天基预警系统的静态拓扑结构网络模型的抗毁性效能用已建立的连通熵测度模型分别进行抗毁性测度,再将整个时间序列里面的抗毁性效能进行综合分析,以描述天基预警系统抗毁性的整体、对抗、动态变化过程,探讨天基预警系统抗毁性的变化规律,揭示它在该时间序列里的固有特征以及与外界之间的关联关系[13]。
图5为天基预警系统在某天内的抗毁性效能值变化曲线。

图5 系统在某天内的抗毁性变化曲线
4.2 灰色关联分析
灰色关联度分析目的是通过一定的方法来寻找系统中各个子系统因素之间的数值关系。因此,灰色关联度对于一个系统发展变化态势提供了量化的度量,比较适合动态天基预警系统的抗毁性测度分析。
利用式(7)归一化处理后得到的影响因素矩阵,如表3所示。

表3 各影响因素标准化序列
由式(8)可以计算得出6个影响因素的抗毁性关系数,如表4所示。

表4 各影响因素的抗毁性关联系数
根据式(9)可计算出各个影响因素对于天基预警系统抗毁性效能的灰色关联度,如表5所示。

表5 各影响因素灰色关联度
从表5可以看出,各影响因素对天基预警抗毁性的灰色关联度都大于0.5,这意味着网络平均度、平均聚类系数、平均路径长度、网络直径、网络全局效率、最大连通子图都是影响抗毁性效能的主要因素。
对各个因素和系统抗毁性的相关影响因素的灰色关联度按从大到小的排序为:X2>X3>X6>X1>X5>X4,其中网络平均聚类系数、平均路径长度、最大连通子图相对而言与天基预警系统抗毁性的关联度较大(均大于0.8),网络平均聚类系数对抗毁性的灰色关联度最大,网络直径与抗毁性的关联度最小。
5 结束语
本文基于熵模型、结合节点结构价值和信息价值,提出了系统网络连通熵抗毁性测度模型,并通过对一段时间序列上的系统网络拓扑结构进行分析,运用网络连通熵模型对动态天基预警系统在一段时间序列上的抗毁性进行测度。
文章利用灰色关联分析方法计算出系统网络抗毁性与主要影响因素的关联度,同时对各个影响因素进行了灰色关联预测,取得了满意效果。在系统网络抗毁性的影响因素中,得到网络平均聚类系数(关联度为0.896)影响最大,提出了一种时间序列离散模型并通过统计转化来分析研动态网络的抗毁性测度问题的新思路,也为分析和研究天基预警系统抗毁性的影响因素、控制因素以达到提高系统网络的抗毁性提供了重要参考。
[1] 郭文鸽,冯书兴.美国导弹预警卫星系统分析及其启示[J].中国航天, 2005(12):39-42.
[2] 谭跃进, 吴俊, 邓宏钟,等. 复杂网络抗毁性研究综述[J]. 系统工程, 2006, 24(10):1-5.
[3] 许松, 闫世强, 刘辉,等. STK在导弹预警卫星仿真中的应用[J]. 舰船电子对抗, 2011, 34(05):76-80.
[4] 熊伟, 简平, 熊伟,等. 以数据为中心的天基预警系统视图模型研究[J]. 指挥控制与仿真, 2013, 35(5):11-16.
[5] 周玉晶,沈嘉荟,邱海韬,等.基于复杂网络的社交媒体内容安全可视化分析系统[J].信息网络安全,2016(9):158-162.
[6] 王喆,彭其渊.成都市公交复杂网络拓扑特性研究[J].交通与计算机,2007,25(2):39-42.
[7] 刘涛,陈忠,陈晓荣.复杂网络理论及其应用研究概述[J].系统工程,2005,23(6):1-7.
[8] 杨琴. 网络拓扑模型的演化机制及抗毁性研究[D]. 郑州:解放军信息工程大学, 2009:25-28.
[9] 谭跃进, 吴俊. 网络结构熵及其在非标度网络中的应用[J]. 系统工程理论与实践, 2004, 24(6):1-3.
[10] 谭跃进, 吴俊, 邓宏钟. 复杂网络中节点重要度评估的节点收缩方法[J]. 系统工程理论与实践, 2006, 26(11):79-83.
[11] 赫南, 李德毅, 淦文燕,等. 复杂网络中重要性节点发掘综述[J]. 计算机科学, 2007, 34(12):1-5.
[12] 于洪涛. 新疆生态足迹动态变化研究[D]. 新疆:新疆财经大学, 2015.
[13] 门玉琢, 于海波, 李显生. 城市道路交通事故宏观影响因素灰色关联预测模型[J]. 机械设计与制造, 2012(12):251-253.
Anti-destructive Measures and Influencing Factors Gray Relational Analysis of Dynamic Space-based Early Warning System Based on Complex Network
YANG Miao-ben, XIONG Wei
(Aerospace Engineering University, Beijing 101416, China)
The model of network entropy survivability is proposed, and the change of the whole, dynamic and confrontation of space-based early warning system is analyzed. The influence system of the factors such as the average degree of the network, the average path length, the clustering coefficient, the network diameter, the global efficiency of the network and the maximum connected subgraphs are constructed and the gray relational analysis is carried out to quantify the anti-The degree of correlation between factors. Finally, an example is given to summarize the influence of various factors on the survivability of space-based early warning system.
complex network; space-based early warning system; network connectivity entropy; dynamic; survivability; gray correlation analysis
1673-3819(2017)06-0011-06
E11-39;O157.5
A
10.3969/j.issn.1673-3819.2017.06.003
2017-09-17
2017-10-23
重点实验室基金(61420100201162010002)
杨苗本(1993-),男,甘肃武威人,硕士,研究方向为通信与信息系统。熊 伟(1971-),男,研究员。

