基于改进小波阈值函数的医学CT图像降噪∗
张元龙 杨 鹏
(1.南昌航空大学信息工程学院 南昌 330000)(2.江西省图像处理与模式识别重点实验室 南昌 330000)
基于改进小波阈值函数的医学CT图像降噪∗
张元龙1,2杨 鹏1,2
(1.南昌航空大学信息工程学院 南昌 330000)(2.江西省图像处理与模式识别重点实验室 南昌 330000)
针对医学CT图像信噪比低的特点,提出了一种基于软硬阈值的混合函数并结合双树复小波变换的优势对图像进行去噪。首先将图像进行多层分解,然后对分解后的高频子带系数进行新阈值处理,最后通过重构还原图像,经过与其他几种方法的对比,此方法取得了较好的处理效果和峰值信噪比(PSNR)并保留了图像的边缘纹理特征。
双树复小波变换;阈值;图像去噪;峰值信噪比
1 引言
医学信息,如临床数据、图像和其他生理信号等已经成为病人护理的重要部分据,无论是在筛查、诊断、治疗和学习等都具有重要的意义和不可替代的价值。而近几年随之信息技术和医疗器械对的快速发展,极大促进医疗技术的进步,如计算机断层扫描(Computerized Tomographic Scanning,CT)、磁共振成像(Magnetic Resonance Imaging,MRI),不同的数码影像处理血管、心血管造影,X线检查,超声诊断成像,单光子发射的核医学影像计算机断层扫描(Single-Photon Emission Computed Tomography,SPECT)和正电子发射断层扫描(Positron Emission Computed Tomography,PET)等成像技术,由于成像技术的复杂性,在成像过程中不可避免因为硬件设施、外接环境等因素导致图像质量不达标,有噪声或者图像不清晰等,给医师诊断带来很大不便,传统有很多处理方法,但结果不太理想,后来随着小波概念的提出、发展逐渐运用到多个领域中,如离散小波变换(Discrete Wavelet Transform,DWT[1])具有多分辨率分析性、时频局部化特性、三个方向性等;平稳小波变换(Stationary Wavelet Transform,SWT[2])具有平移不变性、冗余数据多、三个方向性等特点,但上述几种处理结果后冗余数据多,计算代价过大,方向选择有限、去噪效果以及保留的特征值不明显等等。双树复小波变换[3~5](Dual-Tree Complex Wavelet Transform,DTCWT)本身主要具有很好的方向性、近似平移不变形等特点,但在进行阈值的选取时候比较死板,常用的有硬阈值和软阈值,阈值的选取对图像去噪效果至关重要,阈值大了则会过滤有用信息,阈值过小则会保留较多噪声,对于此问题,此文提出一种新的阈值选取方法,结合硬阈值和软阈值的特点,构造出新的阈值选取函数去去噪。
2 DT-CWT变换原理
双树复小波变换(Dual-tree Complex Wavelet Transform,DTCWT)的概念,于 1998年首次被Kingsbury在其文章中提出,此方法基本保留了复小波变换的近似平移不变性,而且通过采用两个平行滤波器的形式,基本达到了完全重构条件,它的出现攻克了传统离散小波变换平移敏感性和频率混叠的不足之处,Selesnick等在2005年设计出了双树复小波变换分解重构算法,此算法为双树复小波变换应用在图像处理方面提供了重要工具。
双树复小波变换的基本原理如图1所示,双树复小波变换的实部和虚部分别由两个树状的共轭正交滤波器组构成,树A生成实部,而树B生成虚部。复小波可表示为

其中,ψr(t)表示复小波实部,ψi(t)表示复小波虚部。它们都是实函数,双树复小波可以表示为两个独立的实小波变换,包含两个平行的分解树树A、树B。如果ψr(t)和ψi(t)形成希尔伯特对,那么ψr(t)是在一个半频轴可分析的信号。因而根据式(1)可以获得复小波系数如下:

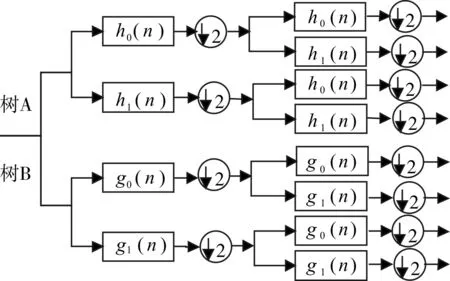
图1 双树复小波变换(DT-CWT)
如式ψ(x,y)=ψ(x)ψ(y),所以

DT-CWT包含两个平行的小波树,即树A树B两个分支。其中上部树A的叠加滤波器组表示复小波变换的实部,下部树B的叠加滤波器组表示复数小波变换的虚部,2表示隔点取样,变换之后的系数同时具有近似平移不变性、系数对应性以及方向各异性的特点,方向性如图2所示。
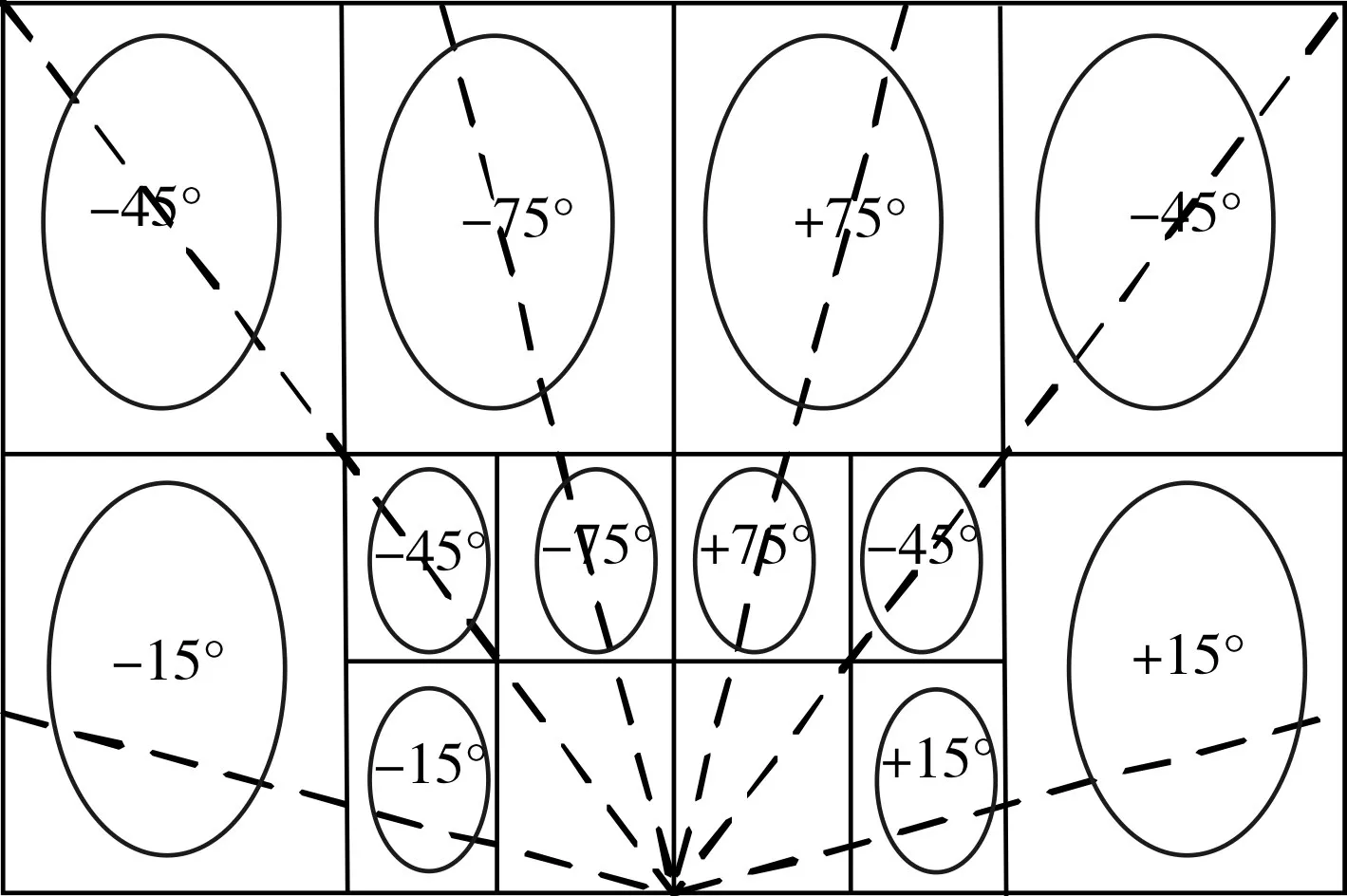
图2 DT-CWT方向性
3 双树复小波阈值去噪
针对去噪问题,去噪函数中的阈值选取尤为关键,选取过小则保留太多噪声,过大则会去除本应保留的信息,传统比较常用的去噪方式有硬阈值和软阈值去噪,硬阈值的核心思想就是把系数幅值大于阈值的小波域系数留下,其他的置零;软阈值的核心思想就是绝对值小于阈值的小波系数幅值置零,大于的在此基础上减去阈值得到新值,小于阈值相反数的则加上阈值作为新值,对应的函数表达式如下所示:
软阈值函数的表达式:

硬阈值的函数表达式:
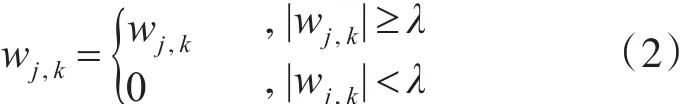
根据此两种阈值的函数表达式,它们各有各的特点,处理的结果各有优缺点,硬阈值去噪,重构的图像结果也许会出现震荡现象;软阈值去噪后,因其在阈值点的函数是连续的,能保留更多特征信息但也因阈值的选取与最优阈值间存在一定皮偏差,因此会使得重构后图像出现模糊情况,因此针对这两种方法的优缺点,本文尝试用文献[6]提出的改进阈值处理方法,优化了阈值的选取

其中,σ为噪声标准方差,N为信号的尺寸或长度,j为分解尺度,当j增加时阈值T随之减少,对应的阈值函数如下,对应如图3所示。

图3 改进后的阈值处理函数图

其中,wj,k为处理后的小波系数,wj,k是小波系数,T为阈值,n为调节参数,f(x)为光滑s型函数,改进后的阈值介于硬阈值和软阈值之间,兼顾了两者的优点,f(x)如下所示:

由式(5)可看出,当 x∈(a,b)时,f(x)∈(0,d)
本文双树复小波阈值去噪由以下步骤组成:
1)利用双树复小波函数对图像进行J层分解,并计算小波系数。首先,对于长度为N的含噪声信号X,不妨设N=2J,利用正交小波变换的快速算法获得低分辨率L(0≤L<J)下的尺度系公式为{vL,k,k=1,…,2L} ,以及各分辨率下的小波系数{wj,k,j=L,L+1,…,L-1,K=1,…,2j},其中尺度系数和小波系数共N个。
2)阈值,j=1,2,…,J ,调节式(3)中的参数 a∈(0,Tj),b∈(Tj,2Tj),分别取一组 (ai,j,bi,j),i=1,2,…,根据j=1确定一个di,j。
3)由 (ai,j,bi,j,di,j)计算出阈值函数表达式,然后对分解后的高频子代系数进行阈值值处理,得出新的单元阵列中下对应方向的数值并保存。
4)重复步骤2)~3),最后得到一个处理后的单元阵列。
5)重构图像
由处理后得到的新单元阵列,通过逆向思路方法,重新构建高频子代系数,结合分解时候分解出的最后一级低通图像数组用双树复小波重构函数重构图像。
4 仿真结果及其性能分析
本文实验素材和实验环境如下:
本文的实验图像来自江西肿瘤医院,图像基本信息和各部分器官的含义如下图所示,实验环境硬件为:联想i7、8G内存;软件环境为:Windows 7、Matlab2014。
实验结果如下:
本文选取了医学上的颈椎图和胸椎器官医学图像作为展示处理效果。对两幅图分别加入噪声方差为10、20、30、40、50的高斯噪声,并分别使用DWT[1]、SWT[2,9]、DTCWT[7~9]、本文等四种方法进行去噪,具体为
1)DWT对图像进行多层分解,采用13、19级过滤器,然后对高频子代系数进行软阈值和硬阈值处理,最后通过重新构建系数利用重构函数还原图像。
2)SWT对图片进行多层分解,然后对对分解后的高频子代系数进行软阈值和硬阈值处理,然后进行逆SWT变换还原图像。
3)DTCWT对图片进行多层分解,采用13,19级过滤器和Q-Shift 14/14级过滤器,然后对分解后的高频子代系数进行软阈值和硬阈值处理,然后重构还原图像。
4)本文采用基于DTCWT对图像进行多层分解,采用13,19级过滤器和qshift_b的Q-Shift 14,14级过滤器,然后对分解后的高频子代系数值进行改进后阈值处理,最后通过重构系数矩阵,利用重构函数还原图像,除了主观效果外还有峰值信噪,图像处理结果图4图5如所示和峰值信噪比如表1表2和图6图7所示。
从图4、图5可以看出,本文的方法在对图像进行有效去噪的同时,还能够很好地保持图像的边缘,关键信息得以保留和增强,细节部分例如图中框线标出的颈椎的边缘等,胸椎图像的边缘细节和部分黑点突出的地方,本文对图片进行多层复分解,可以分别提取每一层每个方向的像素点进行处理,从而得以保留更多的信息。
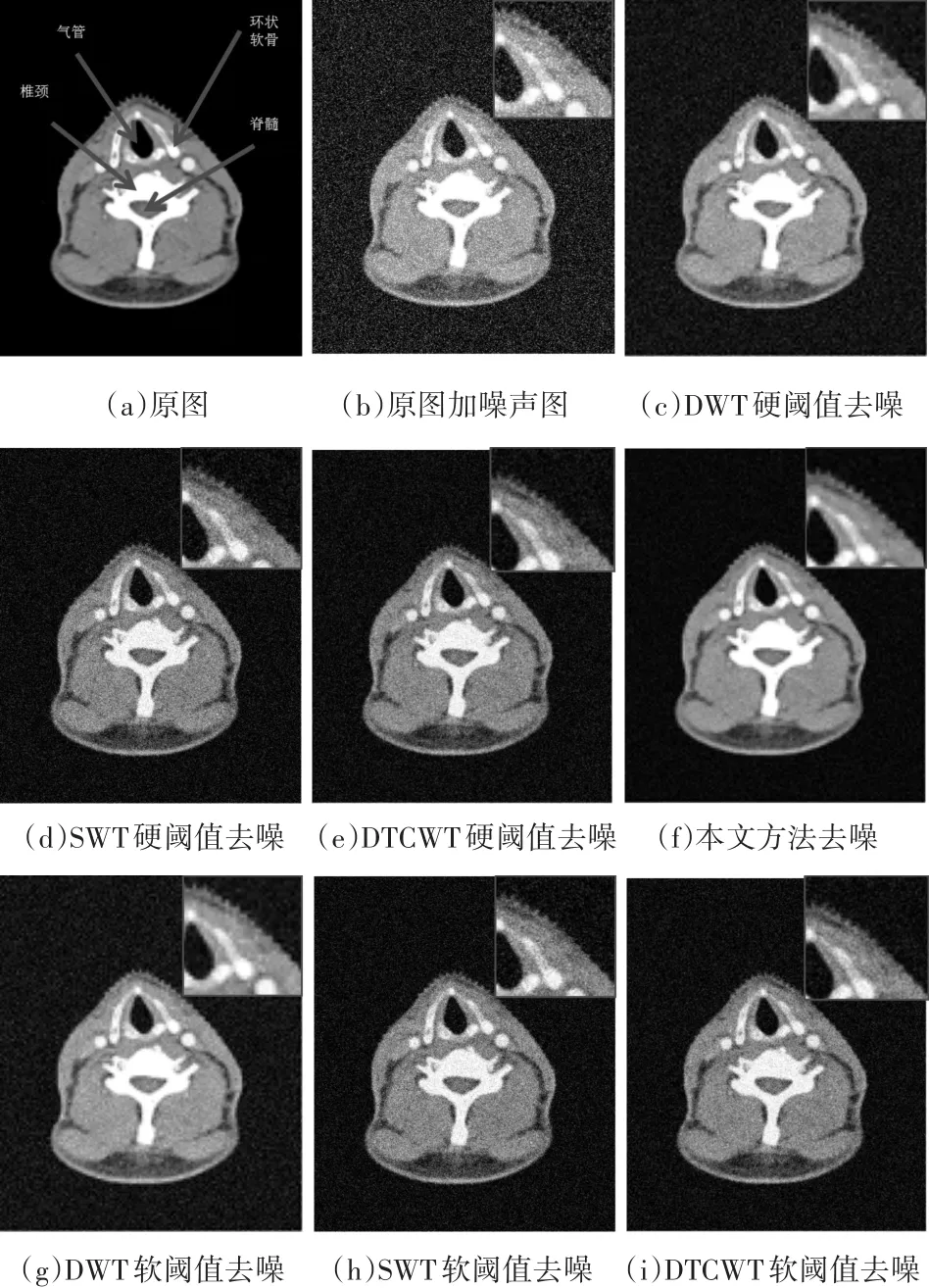
图4 颈椎去噪结果(大小:494×582,添加噪声:高斯噪声,方差:10),3层分解


图5 胸椎去噪结果(大小:972×608,添加噪声:高斯噪声,方差:10),3层分解
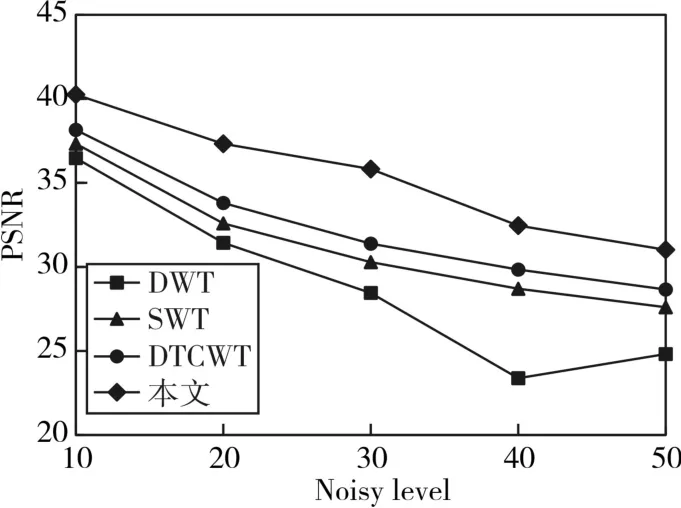
图6 颈椎硬阈值去噪

图7 颈椎软阈值去噪
从表1~表2的数据对比以及图6~图7的折线图可以看出,同一种方法下的硬阈值、软阈值两种处理结果和通过改进阈值后处理的结果相比,本文的处理结果都是比较理想的,特别针对方差较大的噪声图,在处理噪声时相对其他几种去噪能力较好,这个降噪中的峰值信噪比的下降趋势的相对缓慢,由此能保留更多的有用信息,对于医学图像特别是保留病理特征方面具有很好的优势,归功于此方法的平移不变性、良好的方向性选择等特性。
5 结语
医生对医学图像的研究、学习和处理对于确定病人病情是至关重要的,如何更好地去除图像在采集中所受干扰也是至关重要。本研究通过提出了一种基于软硬阈值的混合函数来计算出较理想的阈值,并利用双树复小波变换的多方向性、复小波分解特性对图像进行去噪。用已有方法和本文处理后的实验数据、结果表明,此方法在医学CT噪声图像的处理具有一定的优势,能去除多余的噪声、保留更多的特征纹理信息,但其他方面有待于学习 和改进。
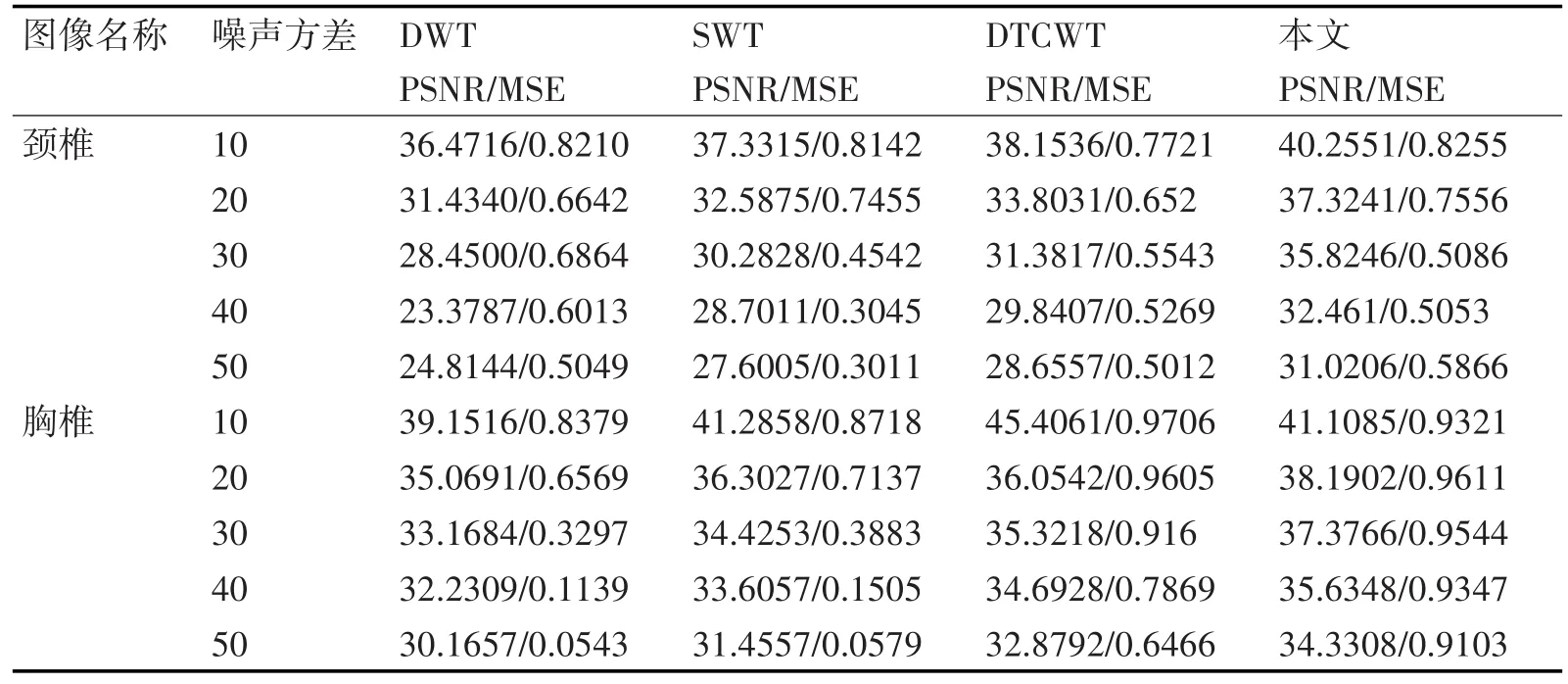
表1 硬阈值去噪结果参数和峰值信噪比
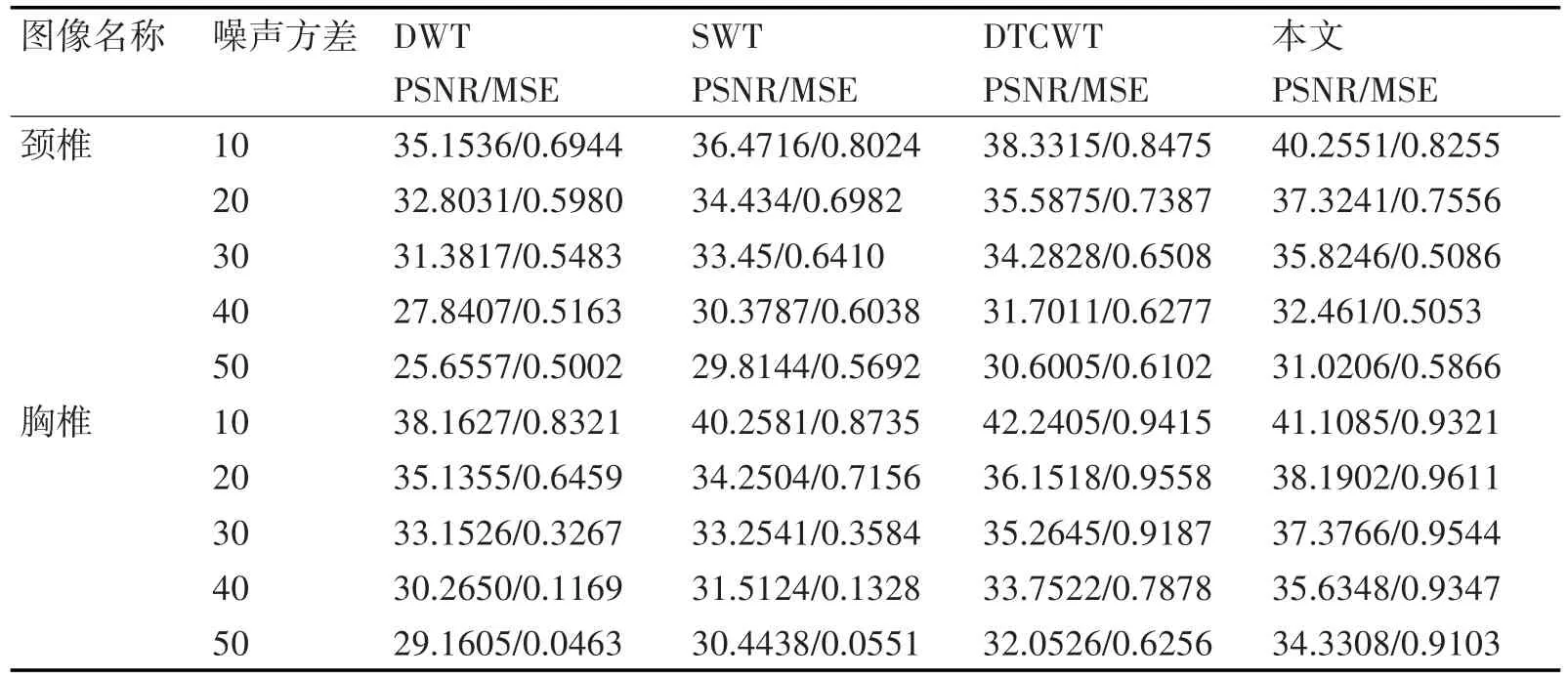
表2 软阈值去噪结果参数和信噪比
[1]张郝.基于小波变换的图像去噪方法研究[D].北京:北京交通大学,2008.ZHAGN Hao.The Research On Image Denoising Based On Wavelet Transform[D].Beijing:Beijing Jiaotong University,2008.
[2]张文革,刘芳,高新波,等.一种自适应多尺度积阈值的图像去噪算法[J].电子与信息学报,2009,31(8):1780-1784.ZHANG Wenge,LIU Fang,GAO Xinbo,et al.An Image Denoising Algorithm Using Adaptive Multiscale Projects Thresholding[J].Journal of Electronics&Information Technology,2009,31(8):1780-1784.
[3]Raj V N P,Venkateswarlu T.Denoising of medical images using dual tree complex wavelet transform[J].Procedia Technology,2012,4:238-244.
[4]Bal U.Dual tree complex wavelet transform based denoising of optical microscopy images[J].Biomedical optics express,2012,3(12):3231-3239.
[5]Singh H,Kaur L,Singh K.Fractional M-band dual tree complex wavelet transform for digital watermarking[J].Sadhana,2014,39(2):345-361.
[6]杨鑫蕊.改进的小波阈值去噪算法研究[D].哈尔滨:哈尔滨理工大学,2014.YANG Xinrui.The Study On Improve Wavelete Threshold Denoising Method[D].Harbin:Harbin University of Science and Technology,2014.
[7]郭巍,张平,陈曦,等.基于双密度双树复数小波变换的合成孔径雷达图像降噪研究[J].电子学报,2009,37(12):2747-2752.GUO Wei,ZHANG Ping,CHEN Xi,et al.Research on Synthetic Aperture Radar Image Denoising With Double Density Dual-Tree Complex Wavelet Transform[J].Acta Electronicasinica,2009,37(12):2747-2752.
[8]刘蕾.基于双树复小波变换的图像去噪[D].北京:北京化工大学,2010.LIU Lei.Image Denoising Based on The Dual Tree Complex Wavelet Transform[D].Beijing:Beijing University of Chemical Technology,2010.
[9]李宁,水鹏郎.一种加窗的双重局部维纳滤波图像去噪算法-基于SWT和DTCWT[J].计算机工程与应用,2007,43(28):44-46.LI Ning,SHUI Penglang.Image Desnoising Algorithm Via Doubly Local Wiener Filtering With Windows Based On SWT And DTCWT[J].computer Endineering and Applications,2007,43(28):44-46.
[10]田园.基于多尺度小波变换的肿瘤图像纹理分析及其临床应用[D].济南:山东师范大学,2015.TIAN Yuan.The Tumor Texture Analysis And Its Clinical Application Based On Multi-Scale Wavelet Transform[D].Jinan:Shandong Normal University,2015.
[11]张国伟.基于小波变换的图像去噪方法研究[D].昆明:昆明理工大学,2014.ZHANG Guowei.The Research On Image Denoising Based On Wavelet Transform[D].Kunming:Kunming University of Science and Technology,2014.
[12]王芳.基于双数复小波变换的微弱生物医学信号处理及其应用研究[D].重庆:重庆大学,2014.WANG Fang.Application of Dual-Tree Complex Wavelet Transform In Weak Biomedical Signal Processing[D].Chongqing:Chongqing University,2014.
[13]Satheesh S,Prasad K.Medical image denoising using adaptive threshold based on contourlet transform[J].arXiv preprint arXiv:1103.4907,2011.
[14]Wang Y,Fu X,Chen L,et al.DTCWT based medical ultrasound images despeckling using LS parameter optimization[C]//2013 IEEE International Conference on Image Processing.IEEE,2013:805-809.
[15]Liu Y,Jiang M.Image denoising algorithm based on DTCWT and adaptive windows[C]//Computer Science and Information Technology(ICCSIT),2010 3rd IEEE International Conference on.IEEE,2010,8:207-210.
Medical CT Image Denoising Based on Improved Wavelet Transform Threshold Function
ZHANG Yuanlong1,2YANG Peng1,2
(1.School of Information Engineering,Nanchang Hangkong University,Nanchang 330000)(2.Key Laboratory of Image Processing and Pattern Recognition(Nanchang Hangkong University),Nanchang 330000)
s According to the characteristics of medical pathology image signal-to-noise ratio is low,this paper proposes a hybrid based on hard and soft threshold function and combining the advantages of dual tree complex wavelet transform for image denoising.First of all,the image is decomposed,then data of each layer undergoes a process with high frequency coefficient threshold,finally,the reconstruction image is restored,Through comparison with several other methods,this method has obtained the good processing effect and peak signal to noise ratio(PSNR)and preserve the edge of the image texture feature.
dual-tree complex wavelet transform(DTCWT),threshold,image denoising,peak signal to noise ratio
TN911
10.3969/j.issn.1672-9722.2017.11.038
Class Number TN911
2017年5月7日,
2017年6月25日
国家自然科学基金项目(编号:61363050,61272077);江西省科技攻关项目(编号:20142BDH80026);南昌航空大学研究生创新基金(编号:YC2015031)资助。
张元龙,男,硕士研究生,研究方向:图像处理与模式识别。杨鹏,男,博士,副教授,研究方向:图像处理与模式识别。

