HCZ产量预测模型在海相砂岩油田的应用——以南海X油田为例

潘 岳，周玉辉，申 健，姚 泽，周文胜，王 凯

（1．中海石油研究总院，北京 100028；2．长江大学；3．中国石油大学（华东））

HCZ产量预测模型在海相砂岩油田的应用
——以南海X油田为例

潘 岳1，周玉辉2，申 健1，姚 泽1，周文胜1，王 凯3

（1．中海石油研究总院，北京 100028；2．长江大学；3．中国石油大学（华东））

南海海相砂岩油藏储量丰富，地质条件优越，目前已开发大量此类油藏。为预测此类油田产量，优化了HCZ产量预测模型的求解方法，在简化计算过程的同时，可以灵活调整模型参数。结合海相低–中黏砂岩典型油田——南海X油田开发实际，针对油田高峰产量后和扩容改造后两个不同产量规律阶段，利用HCZ产量预测模型较为精确地预测出每个阶段的产量，表明了HCZ产量预测模型具有很好的适用性。

海相砂岩；HCZ产量预测模型；阶段产量

南海海相砂岩油藏拥有丰富的储量，已开发的20多个油田的动用探明石油地质储量为 4×108m3；该类油藏拥有构造相对小且简单、储层分布稳定且连通性好、储层物性和原油性质较好、边底水天然能量充足等先天有利的地质条件[1]。南海 X油田作为最早被开发的南海海相低–中黏砂岩油田之一，已有21年的开发经验。对此类老油田展开产量预测工作研究，找到可靠的产量预测方法，可为新油田产量计划编制起到借鉴作用。

目前，预测油田产量方法众多，主要有数值模拟法、Arps递减曲线法和水驱曲线法。数值模拟法涉及的工作繁多，存在诸多不确定性[2–3]；Arps递减曲线法和水驱曲线法都需要油田进入特定阶段时才能使用，并且受人为选择因素影响较大[4–5]。HCZ产量预测模型方法操作简单，可预测油田开发全过程产量[6]，不仅在常规油藏生产中得到了广泛应用[7–9]，而且对超稠油、聚合物驱、煤层气等复杂油气田也具有良好的应用效果[10–12]。但该方法求解时需要两步线性回归，并且预测模型形态不易改变。本文对HCZ产量预测模型求解方法做出改进，并应用在南海X油田海相低–中黏砂岩油田中，预测油田两种产量规律下的产量，取得了良好的预测效果。

1 HCZ产量预测模型

HCZ产量预测模型是由胡建国等人从统计学角度得到，利用油气田实际产量与累积产量数据，预测得到产量、累积产量[6]。

预测模型如下：

式中：Q预测、NP预测为预测产量值和预测累积产量值；!、b为模型参数；NR为预测可采储量，也是模型参数之一；t为时间。

HCZ产量预测模型求解步骤：

（1）第一步线性回归。将实际数据产量Q和累积产量Np代入式（3），绘制关系曲线，线性回归得到截距A和斜率B。利用! =10A，0=B ln10得到模型参数!、0。

（2）第二步线性回归。将实际数据累积产量Np和模型参数b值代入式（4），绘制关系曲线，线性回归得到截距n和斜率m，利用n=lgNR，最终得到可采储量NR。

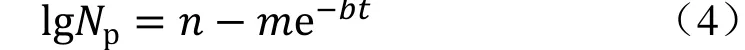
（3）!、b、NR模型参数确定后，代入式（1）、（2）中，可得到HCZ产量预测模型预测指标。

2 算法优化

本文在使用HCZ产量预测模型时，对模型求解步骤进行优化，换了一种求解公式，采用一步线性试差法[13]得到了所求参数。

HCZ产量预测模型算法优化求解步骤：

（1）线性试差法。将实际数据Np代入式（5），绘制关系曲线，通过不断改变NR的值，找到线性关系最优线段，此时NR为所求值；同时得到斜率–0和截距ln!–ln0，从而得到模型参数!和0值。

（2）!、0、NR模型参数确定后，代入式（1）、（2）中，可得到HCZ产量预测模型预测指标。

3 应用实例

3.1 油田概况

南海X油田是典型的南海海相低–中黏砂岩油田，油田属于低幅度披复背斜构造，构造完整简单，圈闭内没有大断层，倾角小于 5°。储层为海相建设性三角洲沉积，分布稳定，连通性好。测井解释油层平均孔隙度为14%～27%，油层平均渗透率为450×10–3～1 861×10–3μm2，属于中高孔、中高渗储层。地层原油密度为0.870～0.888 g/cm3，地层原油黏度为4.0～17.1 mPa·s，属于低～中黏原油性质。油藏具有多套油水系统，块状底水和层状边水交互存在，天然水体能量充足，水体体积倍数基本达到200以上，每采出1%地质储量的压力降为0.008 MPa。

3.2 油田开发特点

南海X油田充分利用油藏有利条件，采用天然能量开采方式，秉持高速开发策略。在开发过程中，通过技术创新实现增储挖潜，实现油田高效开发。

X油田在开发中主要有两个不同产量规律阶段，以平台扩容为分割点。第一阶段：随着开发井陆续投产，南海X油田产量快速上升。第3年油田开发方案中所有井完成投产，第5年油田通过钻补充加密井，完善了开发井网，此时产量到达到了峰值。而后，油田产量开始递减，为了减缓递减，油田采取实施调整井和增产措施（如提液、酸洗和调层补孔等）。第二阶段：油田开发到第11年，通过平台扩容改造，油田再次稳产3年。油田生产数据见表1，开发曲线见图1。

3.3 HCZ产量预测模型的应用

3.3.1 油田产量达到峰值后的产量预测（预测第6年后的产量）

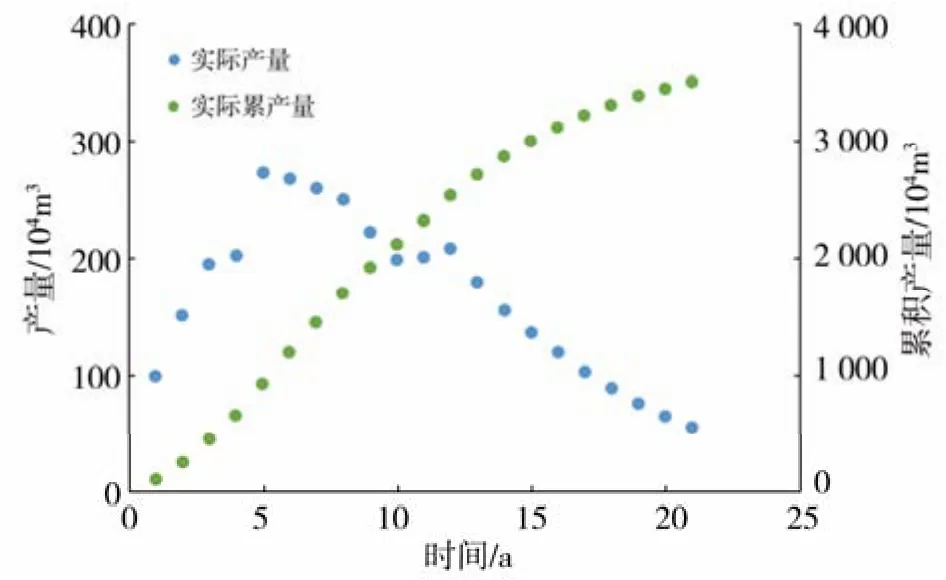
图 1 南海X油田开发曲线

油田产能建设阶段的产量存在不确定性，HCZ产量预测模型也达不到有效的预测。油田产量达到峰值后，产量还没有出现递减，含水比较低，Arps预测方法和水驱曲线法都没法准确预测产量，但HCZ产量预测模型可以通过拟合已产生的实际产量预测出未来产量。

（1）假设只有5年的X油田实际数据，选取第2年到第 5年的实际累积产量 Np，计算得到ln[ln(Np/NR)]，绘制一条与时间t的关系曲线。当可采储量NR=3 150×104m3时，得到一条线性关系较好的曲线，如图2。此时直线斜率为–0.238 0，截距为1.400 3，因此，模型参数!=0.965 4，0=0.238 0。

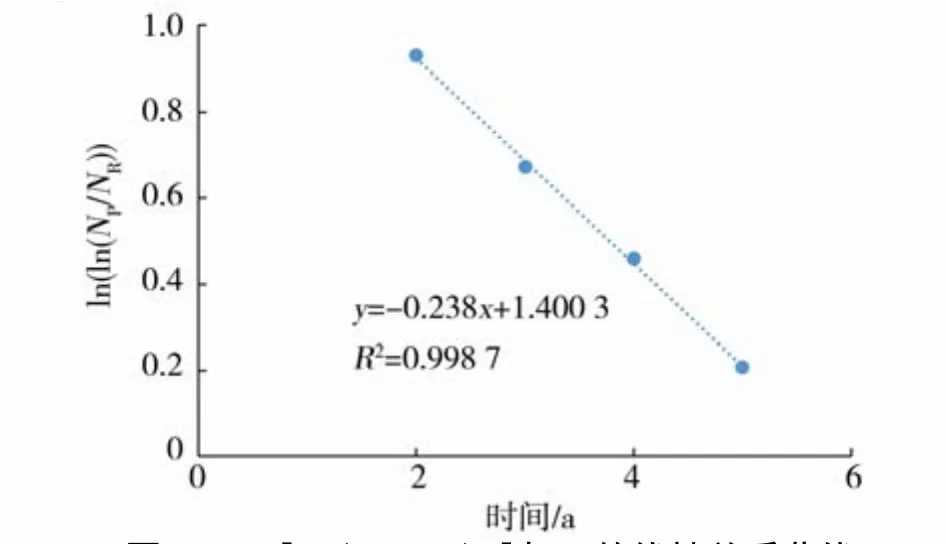
图 2 ln[ln(N P/N R) ]与t的线性关系曲线

（2）将NR、!和b值代入式（1）、（2）中，得到预测产量Q预测和预测累积产量值，列于表1 HCZ预测初期项目中，并绘制出对比图3。

（3） 第6年到第10年的产量预测偏差小于3%（表2），预测精度较高。

3.3.2 油田大型调整后的产量预测（预测第13年后的产量）

海上油田受海上平台液处理能力限制，油田产液量会达到极限而无法通过提液来稳产，所以，平台扩容改造可释放油田产能，同时油田产量规律将发生变化。HCZ产量预测模型对变化后的产量也能做到很好的预测。

（1）假设只有12年的X油田实际数据。选取第 2年到第 12年的实际累积产量 Np，计算得到ln[ln(Np/NR)]，绘制一条与时间t的关系曲线。当可采储量NR=3 930×104m3时，得到一条线性关系较好的曲线，如图4。此时直线斜率为–0.178 9，截距为1.302 2。因此，模型参数!=0.657 9，参数b=0.178 9。

表 1 南海X油田实际产量与预测结果对比

表2 实际产量与预测产量数据偏差分析 104 m3

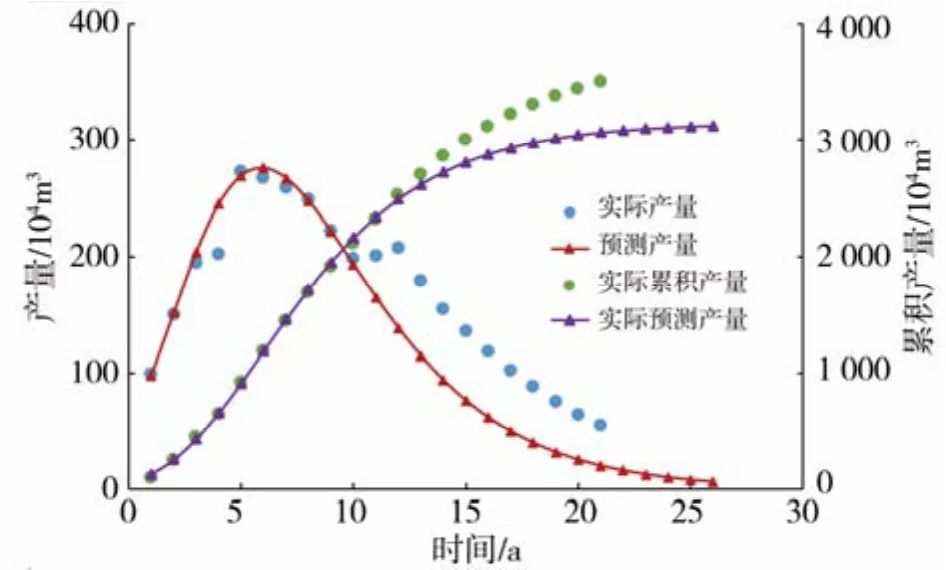
图3 实际数据与预测数据对比

（2）将NR、!和b值代入式（1）、（2）中，得到预测产量Q预测和预测累积产量NP预测值，列于表1的HCZ预测扩容项目中，并绘制出对比图（图5）。

（3） 第13年到第17年的产量预测偏差小于2%（表3），预测精度较高。

表3 实际产量与预测产量数据偏差分析 104m3

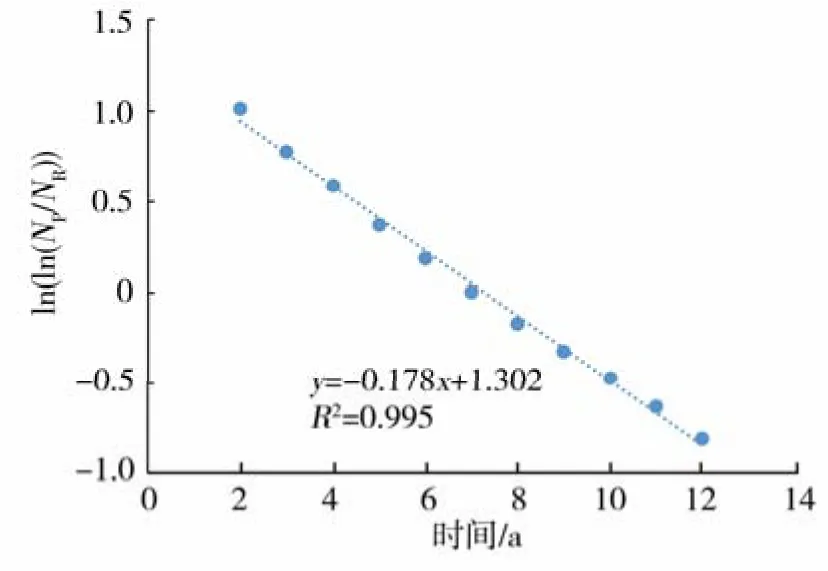
图 4 ln[ln(N p/N R )]与t的线性关系曲线

4 结论

（1）基于HCZ产量预测模型，优化了算法，在简化计算过程的同时，灵活调整模型参数，从而提高产量预测效果。

图 5 实际数据与预测数据对比

（2）模型求解时，通过调整拟合段选择和模型参数NR值来改变模型形态，当预测模型形态与实际数据吻合且实际数据最后一个点与预测数据最为接近时，预测结果达到要求。

（3）南海 X油田实例表明，HCZ产量预测模型可以很好地预测出该油田高峰产量和扩容改造后5年的产量，预测偏差小于3%，符合产量预测要求。

[1] 周守为．中国近海典型油田开发实践[M]．北京：石油工业出版社，2009：135–170.

[2] 潘举玲，黄尚军，祝杨，等．油藏数值模拟技术现状与发展趋势[J]．油气地质与采收率，2002，9（4）：69–71.

[3] 靳彦欣，林承焰，贺晓燕，等．油藏数值模拟在剩余油预测中的不确定性分析[J]．中国石油大学学报（自然科学版），2004，28（3）：22–24.

[4] 陈元千，李璗．现代油藏工程[M]．北京：石油工业出版社，2001：127–161.

[5] 陈元千，杜霞．水驱曲线关系式的对比及直线段出现时间的判断[J]．石油勘探与开发，1986，13（6）：59–67.

[6] 胡建国，陈元千，张盛宗．预测油气田产量的新模型[J]．石油学报，1995，16（1）：79–86.

[7] 陈元千，郝明强．HCZ模型在多峰预测中的应用[J]．石油学报，2013，34（4）：747–752.

[8] 刘鹏程．预测水驱油田含水率的一种新模型[J]．新疆石油学院学报，2000，12（2）：29–32.

[9] 周鹏，陈小凡，乐平，等．几种油气田产量预测模型的对比[J]．新疆石油地质，2012，33（4）：476–478.

[10] 包连纯，国力刚．HCZ产量增长模型在超稠油开采中的应用[J]．特种油气藏，2002，9（6）：6–7.

[11] 刘朝霞，张禹坤，蒋平．Weibull与HCZ预测模型在聚合物驱产油量预测中的应用[J]．油气地质与采收率，2007，14（6）：76～78.

[12] 张海茹，李昊．煤层气峰值产量拟合及产量动态预测方法研究[J]．岩性油气藏，2013，25（4）：116–118.

[13] 陈元千．对翁氏预测模型的推导及应用[J]．天然气工业，1996，16（2）：22–26.

TE323

A

1673–8217（2017）06–0078–04

2017–05–27

潘岳，工程师，1986年生，2012年毕业于西南石油大学油气田开发专业，现从事老油田动态研究工作。基金项目：“十三五”国家科技重大专项“海上稠油油田开发模式研究”（2016ZX05025001）。

王金旗