决策演化集的膜结构

胡玉文 徐久成 徐天贺

(1.河南师范大学计算机与信息工程学院, 新乡, 453007; 2.河南省高校计算智能与数据挖掘工程技术研究中心, 新乡, 453007; 3.河南师范大学图书馆, 新乡, 453007)

决策演化集的膜结构

胡玉文1,2,3徐久成1,2徐天贺1,2

(1.河南师范大学计算机与信息工程学院, 新乡, 453007; 2.河南省高校计算智能与数据挖掘工程技术研究中心, 新乡, 453007; 3.河南师范大学图书馆, 新乡, 453007)

决策演化集是处理决策规则在时间序列上演化问题的理论,它将着眼点从静态决策信息系统转移到动态时间序列上，研究决策信息系统随时间变化的演化规律，是一种新的决策规则研究方法。目前，在决策演化集的标准结构下，其定义的演化轨迹是一个很难描绘的n维空间图形，所以本文提出了膜结构重新描述决策演化集，在膜结构下,被约简掉的属性同样会获得重视。在当时间从ti-1进入ti时，属性根据自身对决策的影响而进入不同的膜，同时所产生的数据流动也被标记出来,从而解决了决策信息系统演化轨迹具象化的问题，并通过实例演示了决策信息系统的演化过程和轨迹。

粗糙集；粒度决策；决策演化；膜结构

引 言

伴随着当今信息化社会的快速发展，数据挖掘和人工智能越来越受到重视与青睐。在数据挖掘和人工智能的许多方法中，粗糙集作为一种有效的方法在信息科学领域处理复杂系统时被广泛应用，具有很强的生命力。经典粗糙集理论的一大特点是研究多集中在对静态信息系统的处理上[1-5]，但不能忽视和值得注意的是，现实中的数据库大多是动态的，随着时间不断地变化着。很多学者也开始将粗糙集、粒计算同时间序列相结合，提出了很多方法[6-12]，其主要指导思想是去除动态数据表中数据对于时间的依赖性，将除去时间依赖性的数据重新组织为一个静态数据表，并使用粗糙集中的属性约简和规则提取方法对新形成的静态数据表进行处理。这些方法同经典粗糙集很相似，最后的结果还是对静态数据表的处理，但在把动态数据表转换为静态数据表的过程里忽略了除去的时间依赖性中所蕴藏的信息。文献[13]在对时间序列数据进行分析预测时利用了F-变换和模糊趋势模型。文献[14]把着眼点放在被传统方法忽略掉的时间依赖性上，没有拘泥于属性约简和规则提取上，而是将动态数据表进行时间粒度划分，并对每个时间粒产生的相关规则进行研究，发现其中的相关性，从而提出了粒度决策演化模型。文献[15]在粒度决策演化模型的基础上对演化过程中的属性进行分类，提出了决策演化集，并建立了粒度决策代数描述和粒度决策演化矩阵。虽然文献[15]创建了时间序列下粒度决策的演化理论，给出了决策信息系统演化轨迹的概念，而且对决策信息系统的演化过程进行了多方面的研究[16-21]，但是在标准定义下，决策信息系统的演化轨迹是一个n维空间的图形，很难具象化出来。然而演化轨迹的绘制有着其实际的意义，它可以帮助人们更好地观察决策信息系统的演化趋势，各个节点的稳定状态和数据交换的情况，因此本文将就演化轨迹具象化的问题展开研究。

1 预备概念

定义1[14]在决策信息系统S=(U，C∪D)在时间序列存在时间粒gi，gi+1∈G={g1,g2, …,gm}，在粒gi，gi+1存在决策规则Decision_lgi→f和Decision_lgi+1→f，|Decision_lgi+1∩Decision_lgi|同|Decision_lgi|比值称为gi+1相对于gi的属性继承度，记为InA(gi+1|gi)。

定义2[14]在决策信息系统S=(U，C∪D)在时间序列存在时间粒gi∈G={g1,g2, …,gm}，粒gi存在Decision_l→f，c∈Decision_l，将c在G中所有Decision_l→f出现次数与决策规则总数的比值称为c相对于决策属性f的支持度，简称属性支持度，记为Sup_D(c|f)。

定义3[14]在决策信息系统S=(U，C∪D)中，c∈C。对于Decision_l→f，由所有属性支持度为Sup_D(c|f)=1的c组成的集合称为决策f的属性支持核，记为coreS(f)。

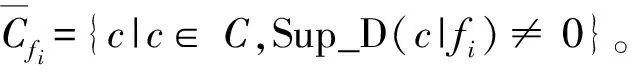
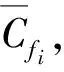
定义9[15]时间序列T={t1,t2, …,ti,ti+1, …}，决策fi∈D，则矩阵E被称为决策fi的演化矩阵

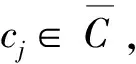
定义10[15]时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U,C∪D)，在时间点ti下决策fi的演化矩阵为Eti= [Cont1,Cont2, …,Conti]，其中列向量ConXj= (e1,e2, …,en)tj，tj∈T，cm∈C(m=1,2,…,n)。则时间点ti+1下决策fi的演化矩阵为Eti+1= [Eti,Conti+1]，其中列向量Conti+1= (e1,e2,…,en)ti+1，ti+1∈T。

定义11[15]时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U,C∪D)，决策fi演化矩阵Eti= [Eti-1,Conti]，支持度向量st(i-1, i)= (Sup_Dti(c1|fi), Sup_Dti(c2|fi), …, Sup_Dti(cn|fi))，则cosθ= (st(i-1, i)·Conti) / ‖st(i-1, i)‖·‖Conti‖，称θ为决策fi在时间点ti的支持度夹角。

定义12[15]时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U,C∪D)，决策fi演化矩阵Eti= [Eti-1,Conti]，Eti+1= [Eti,Conti+1]，预测向量fore(ti, ti+1)=(c1,c2,…,cn)，则cosα= (fore(ti, ti+1)·Conti+1) / ‖fore(ti, ti+1)‖· ‖Conti+1‖，称α为决策fi在时间点ti+1的偏移夹角。

定义13[15]时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U,C∪D)，决策fi演化矩阵Eti= [Eti-1,Conti]，预测向量fore(ti-1, ti)=(c1,c2,…,cn)，支持度向量st(i-1, i)= (Sup_Dti(c1|fi), Sup_Dti(c2|fi),…, Sup_Dti(cn|fi))，则cosβ= (fore(ti-1, ti)·st(i-1, i)) / ‖fore(ti-1, ti)‖ · ‖st(i-1, i)‖，称β为决策fi在时间点ti的预测支持夹角。

定义14时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U,C∪D)，决策fi的演化矩阵Eti= [Eti-1,Conti,Conti+1]，则cosγ= (Conti,Conti+1) / ‖Conti‖ · ‖Conti+1‖，称γ为决策fi在时间点ti+1的相对于时间点ti的演化夹角。

定义15时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U,C∪D)，决策fi的演化矩阵Eti= [Eti-1,Conti,Conti+1]，预测向量fore(ti, ti+1)=(c1,c2,…,cn)，则cosφ= (fore(ti, ti+1)·Conti) / ‖fore(ti, ti+1)‖· ‖Conti‖，称φ为决策fi在时间点ti的预测夹角。

图1 膜的结构Fig．1 Membrane structure

2 决策演化集的膜结构

2.1 膜计算的基本理论

许多计算机科学领域的突破性进展都来源于自然界的启发，这些进展不仅在理论上而且在实际应用中均引起了广泛关注。作为自然计算范围内一个新分支，正随着其发展产生了大量的计算框架，为生物分子计算提供了大量工具。虽然活细胞的结构是启发膜计算模型的源泉，但得到丰富的计算模型才是研究膜计算的目的，正如计算理论在计算机科学研究中所处的地位一样。

膜计算下的膜结构由主膜及主膜内按层次机构排列的膜组成，内部被这些膜划分成若干个区域。就像在生物学中常见到的活细胞一样，膜结构其实是一种三维的囊泡形式，实际中经常使用平面的文氏图来描述膜的结构，如图1所示。由此，膜系统的计算可以定义为：它开始于膜系统的某个初始格局，计算可以随着格局传递下去，直到在输出膜中出现计算结果时终止。

膜系统具有如下的形式：∏ = (O,μ,ω1, …,ωm,R1, …,Rm,io)。式中：O表示一个字母表，其元素称为对象；μ表示由m个膜组成的膜结构，每个膜(或者区域)对应的标号依次为1，2，…，m，m称为∏系统的度数；ωi(1 ≤i≤m)表示在初始状态下存在区域1，2，…，m中的字符串，这些字符串表示O上的多重集；Ri(1 ≤i≤m)为字母表O上的进化规则的有限集合；Ri对应于其中区域i的进化规则集合；进化规则形如u→υ，u为O上的字符串，υ为Otar上的字符串，Otar=O×TAR，TAR = {here, out}∪{inj|1 ≤j≤m}；io∈ {1，2，…，m}是一个基本膜(输出膜)的标记；符号here，out，inj，1 ≤j≤m被称为目标命令或者目标指令，u的长度被称为规则u→υ的半径。如果∏中的规则半径大于1，则称之为协作系统，否则称之为非协作系统。

2.2 决策演化集的膜结构

时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U，C∪D)，决策fi∈D，在时间点ti下，决策fi的约简属性组成的约简属性集为Reduceti，决策规则中的属性组成决定属性集为DecideXi。在时间点ti+1下，约简属性集为Reduceti+1，决定属性集为Decideti+1，Reduceti和Reduceti+1之间，Decideti和Decideti+1之间并不一定相等，但Reduceti∪Decideti=Reduceti+1∪Decideti+1=C，所以当时间从ti到ti+1时，约简属性集Reduce和决定属性集Decide之间存在着数据交换和进化规则。

时间序列T={t1,t2, …,ti,ti+1, …}，决策表信息系统S=(U，C∪D)，决策fi∈D的膜结构具有如下形式：∏ti= (C, [surface[reduce]reduce[decide]decide]surface,ωreduce,ωdecide,Rreduce,Rdecide, decide)。式中：C为决策表信息系统的条件属性集；[surface[reduce]reduce[decide]decide]surface为决策演化集的膜结构，[surface]surface表示表层膜，[reduce]reduce，[decide]decide表示基本膜；ωreduce,ωdecide分别是膜[reduce]reduce和[decide]decide中的字符串；Rreduce和Rdecide分别对应[reduce]reduce和[decide]decide中从时间点ti到ti+1的演化规则，进化规则形如u→υ，u为C上的字符串； decide表示基本膜[decide]decide为输出膜。

依据上述定义，可得决策演化集的膜结构示意图，如图2所示。

图2 时间粒gi到gi+1的决策演化集的膜结构Fig．2 Membrane structure of decision evolution sets from time granule gi to gi+1

对于决策表信息系统S=(U，C∪D)，当时间序列从ti到ti+1，两个临近的时间粒分别为gi和gi+1，决策f分别从时间粒gi和时间粒gi+1得到规则Decisiongi→f和Decisiongi+1→f，所以根据膜结构的定义可知Decisiongi=ωdecide，C-ωdecide=ωreduce，ωdecide∪ωreduce=C，Rdecide为Decisiongi到Decisiongi+1的进化规则。Rreduce为C-Decisiongi到C-Decisiongi+1的进化规则。

当决策演化集从时间点ti移动到时间点ti+1时，演化流程如图3所示。图3中存在着时间粒gi-1到gi和时间粒gi到gi+1的实体膜，同时还存在着在时间粒gi到gi+1的预测膜，α为时间点ti+1相对于ti的演化夹角，β为偏移夹角，θ为预测夹角。

图3 膜结构下决策演化集演化流程图Fig．3 Evolution processes of membrane structure of decision evolution sets

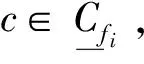
2.3 实例解析

设时间序列T={t1,t2, …,ti,ti+1,…}，在时间点ti下，决策信息系统S=(U,C∪D)，条件属性集C= {a,b,c,d,e,h,k,l,m,n}，决策属性集D= {q}，每个属性c∈C∪D的值域Vc= {0, 1, 2}。对决策信息系统S在时间序列下进行粒度划分得到粒集，时间子粒gi(i=1, 2, 3, 4, 5, 6)进行规则提取处理，结果如表1所示。

表1 决策信息系统各个时间粒的决策规则

对表1进行数据处理，将决策q0，q1和q2的决策规则分别集合在一起，结果如表2所示。

表2 按决策属性整理的各个时间粒的决策规则

以决策q0为观察点来解释说明决策演化集膜结构的工作方法。由表2和定义9可以得到决策q0在不同时间点ti(i=1,2,3,4,5,6)下的演化矩阵分别为

在时间点ti得到决策信息系统S从时间粒g5到g6的实体膜结构如图4所示。

图4 时间粒g5到g6的实体膜结构Fig．4 Real membrane structure of decision evolution sets from time granule g5 to g6

将决策q0下各属性的继承度组成序列I={3/10, 1/5, 1/5, 3/10, 3/10}，在时间序列T={t1,t2, …,ti,ti+1}的时间点ti+1下新增加的时间粒g7对g6的属性继承度InA=13/50，所以Conti+1中非零元素的个数∈[2，3]。支持度向量st(6,7)= (1/2, 2/3, 1/2, 1, 1/3, 1/3, 2/3, 1/2, 1/2, 1/2)，预测向量

fore(6, 7)1=(0, 1, 0, 1, 0, 0, 0, 0, 0, 0)，
fore(6, 7)2=(0, 0, 0, 1, 0, 0, 1, 0, 0, 0)，
fore(6, 7)3=(0, 1, 0, 1, 0, 0, 1, 0, 0, 0)，

所以

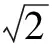
所以在时间点ti给出的下一个时间点ti+1新增时间粒g7的条件属性向量为Cong7= (0, 1, 0, 1, 0, 0, 1, 0, 0, 0)，预测夹角θ=45°。预测的膜结构如图5所示。

得到演化矩阵

图5 时间粒g6到g7的预测膜结构Fig．5 Forecast membrane structure of decision evolution sets from time granule g6 to g7

粒决策规则g7c1d0e2h2l0n1→q0a2b1c2k1m0n0→q1b1c0d1e2k2l0n1→q2

所以对于决策q0，得到的实际的时间粒g6到时间粒g7的膜结构如图6所示。

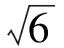
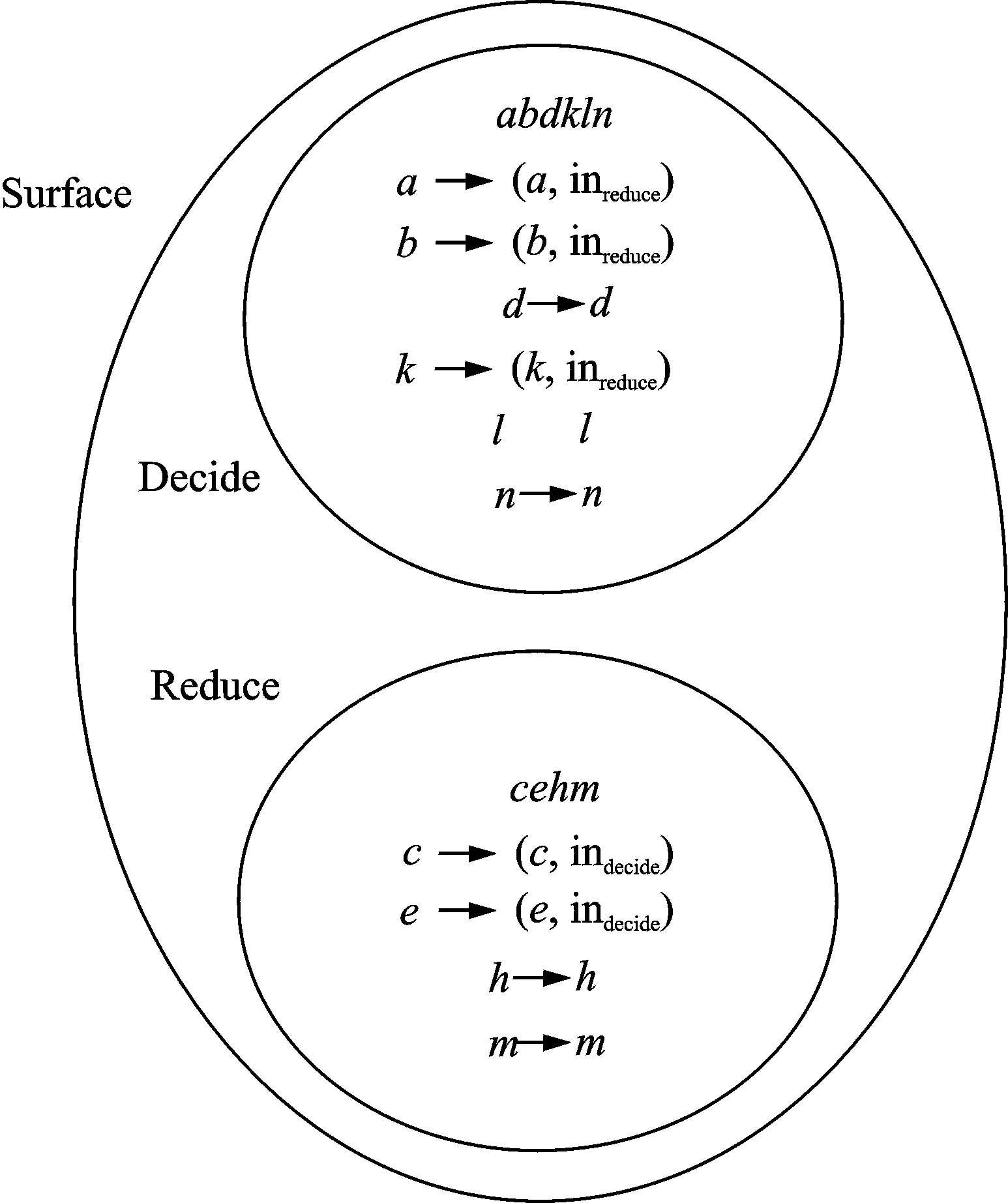
图6 时间粒g6到g7的实体膜结构Fig．6 Real membrane structure of decision evolution sets from time granule g6 to g7

粒决策规则g8b0d0h1k1m2n1→q0b1c0d2l2m0→q1c0d2e1h0k0m2→q2

所以对于决策q0得到的实际的g7到时间粒g8的膜结构如图7所示。图3所示的决策演化集膜结构在本例中就具体化为图8。其中演化夹角α1=60°，偏移夹角β=76.37°，预测夹角θ=45°，演化夹角α2=60°。

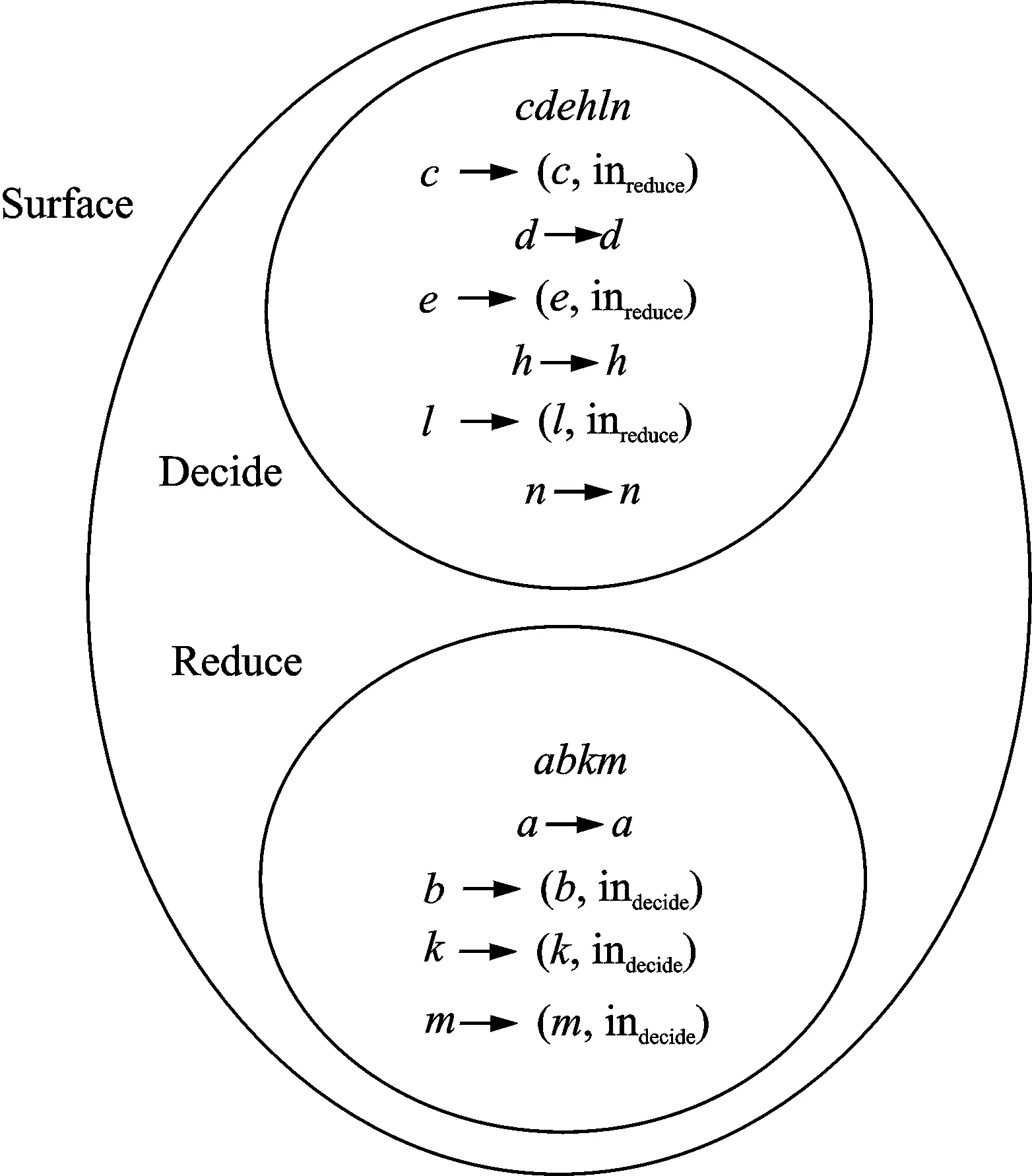
图7 时间粒g7到g8的实体膜结构Fig．7 Real membrane structure of decision evolution sets from time granule g7 to g8

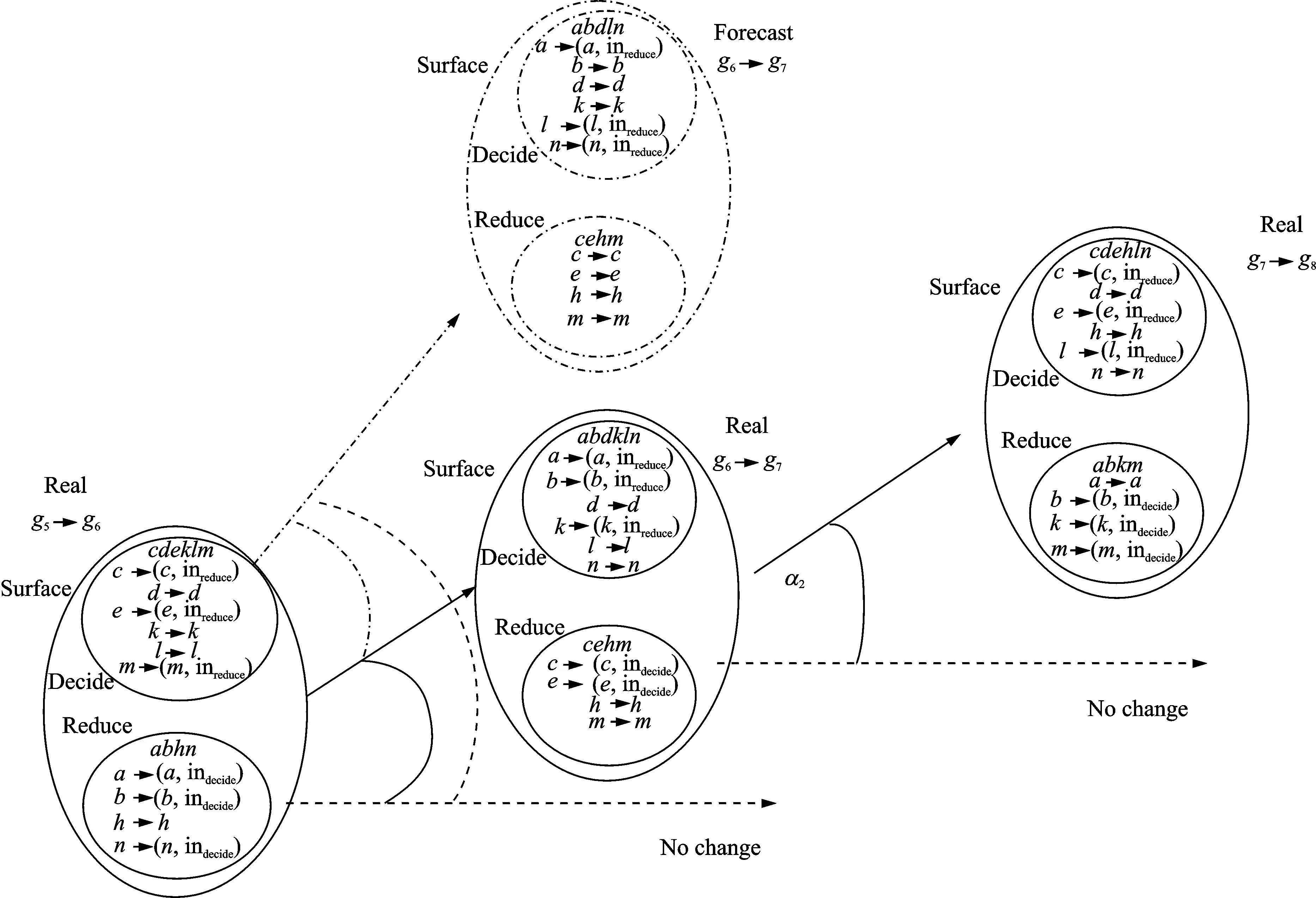
图8 决策演化集的膜结构实例演化流程图Fig．8 Illustration of evolution process of membrane structure of decision evolution sets

3 决策演化集膜结构特点

文献[15]提出了决策演化集的概念，并且给出了演化轨迹的定义，但对于具有n个条件属性的决策信息系统，其演化轨迹是一个n维空间下的路径，虽然存在，但很难具体地描绘出来。而使用膜结构对决策演化集进行描述后，决策信息系统的演化轨迹得以具象化，其演化轨迹可以清晰地展示出来。同时由于在膜结构中存在决策膜(Decide)和约简膜(Deduce)，在演化轨迹得以具现化的同时，也将在演化过程中的数据交换过程展现出来。在传统的对决策信息系统的研究中，通常注意到时间粒里面的某些条件属性决定了一个决策，而另外的一些条件属性则被约简。而这些条件属性在下一个时间粒里对于决策属性的权重则会改变，而这些改变的过程虽然在文献[15]中进行了研究，但是却没有实际展示出来，而利用膜结构则可以把这个属性转换的过程直观地表示出来。

同时，在膜结构下，演化轨迹中的每一个实体膜的背后，还隐藏着一个预测膜，如图3和图6所示。在文献[19]中，研究了粒度决策演化模型的决策稳定性问题，并且利用博弈论的方法，对预测结果和实际结果之间进行了评估，同时指出预测结果和实际结果会对决策信息系统的稳定造成影响，但同样的没有具象化这种现象。而在膜结构下，一个膜结构节点下，存在着实体膜和预测膜，从而将文献[19]所描述的预测结果和实际结果之间的这种关系展现了出来，可以清楚地看到决策信息系统在某个节点的稳定状态。在演化轨迹具象化之后，相应的预测夹角、演化夹角和偏移夹角都可以具象化出来，这对于观察演化轨迹的走势很有帮助，也能更为方便地研究决策信息系统的演化态势。

4 结束语

本文提出的决策演化集的膜结构解决了决策信息系统演化轨迹的具象化问题，然而对于决策演化集来说，在膜结构下依然还有很多的问题要解决，例如膜结构下每个规则的进化优先次序，促使膜结构下进化规则产生的促进剂，以及当预测膜和实际膜不同时产生不稳定的抑制剂问题，膜结构下决策演化集的计算能力和计算效率等问题都非常值得继续研究。

[1] 黄海, 王国胤, 吴渝. 一种不完备信息系统的直接约简方法[J]. 小型微型计算机系统, 2005, 26(10): 1761-1769.

Huang Hai, Wang Guoyin, Wu Yu. Direct reduction method for incomplete information system [J]. Mini-Micro System, 2005, 26(10): 1761-1769.

[2] 王国胤. 决策表核属性的计算方法[J]. 计算机学报, 2003, 26(5): 611-615.

Wang Guoyin. Calculation methods for core attributes of decision table[J]. Chinese Journal of Computer, 2003, 26(5): 611-615.

[3] 赵军, 王国胤, 吴中福. 一种高效的属性核计算方法[J]. 小型微型计算机系统, 2003, 24(11): 1950-1953.

Zhao Jun, Wang Guoyin, Wu Zhongfu. An efficient approach to compute the feature core[J]. Mini-Micro System, 2003, 24(11): 1950-1953.

[4] 闫德勤. 不相容信息系统的规范化格式与差别矩阵[J]. 计算机工程与应用, 2004, 40(36): 45-46.

Yan Deqin. Standardization of discontent information systems and discernibility matrix[J]. Computer Engineering and Application, 2004, 40(36): 45-46.

[5] 徐凤生, 李海军. 不相容决策表的求核方法[J]. 计算机工程与科学, 2007, 29(11): 84-85.

Xu Fengsheng, Li Haijun. A method of finding the core for inconsistent decision tables[J]. Computer Engineering & Science, 2007, 29(11): 84- 85.

[6] Matsumoto Yoshiyuki, Watada Junzo.Knowledge acquisition from time series data through rough sets analysis[J]. International Journal of Innovative Computing, Information and control, 2009,5(12):4885-4897.

[7] Pancerz Krzysztof, Lewicki Arkadiusz, Tadeusiewicz Ryszard. Ant based clustering of time series discrete data—A rough set approach[C]//2nd International Conference on Swarm, Evolutionary, and Memetic Computing．Visakhapatnam, Andhra Pradesh, India: Springer Verlag, 2011: 645-653.

[8] Luo Aibao, Jia Xiuyi, Shang Lin, et al. Granular-based partial periodic pattern discovery over time series data[C]// 6th International Conference on Rough Sets and Knowledge Technology. Banff, AB, Canada: Springer Verlag, 2011: 706-711.

[9] Kong Lingshuang, Yang Chunhua, Wang Yalin, et al. Generic phase space reconstruction method of multivariate time series[C]∥2009 Chinese Control and Decision Conference. Guilin, China: IEEE Computer Society, 2009: 3752-3755.

[10] Kaneiwa Ken, Kudo Yasuo.Local pattern mining from sequences using rough set theory[C]//2010 IEEE International Conference on Granular Computing． San Jose, CA, United States: IEEE Computer Society, 2010: 247-252.

[11] Cheng Chinghsue, Chen Tailiang, Wei Liangying. A hybrid model based on rough sets theory and genetic algorithms for stock price forecasting[J]. Information Sciences, 2010,180(9):1610-1629.

[12] Bang Y K, Lee C H. Design of adaptive prediction system based on rough sets[C]∥2009 IEEE International Conference on Fuzzy Systems． Jeju Island, Korea:IEEE,2009:1914-1919.

[13] Perfilieva Irina, Yarushkina Nadezhda, Afanasieva Tatiana, et al. Time series analysis using soft computing methods[J]. International Journal of General Systems, 2013,42(6):687-705.

[14] 胡玉文, 徐久成, 张倩倩. 多粒度时间序列下粒度决策的演化模型研究[J]. 计算机工程与应用, 2011, 47(20): 117-120.

Hu Yuwen, Xu Jiucheng, Zhang Qianqian. Research on evolution model of granular decision based on multiple time granularity[J]. Computer Engineering and Application, 2011, 47(20): 117-120.

[15] 胡玉文, 徐久成, 孙林.决策演化集研究[J]. 广西师范大学学报(自然科学版),2013, 31(3): 23-29.

Hu Yuwen, Xu Jiucheng, Sun Lin. Decision Evolution Sets[J]. Journal of Guangxi Normal University(Natural Science), 2013, 31(3):23-29.

[16] 胡玉文. 时间序列下决策表信息系统演化模型研究[D]. 新乡: 河南师范大学, 2010.

Hu Yuwen. Research on evolvement model of information system of decision table based on time series [D]. Xinxiang: Henan Normal University, 2010.

[17] 胡玉文, 徐久成, 张倩倩. 决策表信息系统演化模型的回归分析预测算法[J]. 煤炭技术,2010,29(9): 152-153.

Hu Yuwen, Xu Jiucheng, Zhang Qianqian. Pre-sentient algorithm of regression analysis based on evolvement model of information system of decision table[J]. Coal Technology, 2010,29(9): 152-153.

[18] 胡玉文, 徐久成, 李双群. 粒度决策演化模型的博弈选择研究[J]. 计算机工程与应用, 2012, 48(29): 51-54.

Hu Yuwen, Xu Jiucheng, Li Shuangqun. Research on game selection of evolution model of granular decision[J]. Computer Engineering and Application, 2012, 48(29): 51-54.

[19] 胡玉文, 徐久成, 孙林. 粒度决策演化模型的决策稳定性研究[J]. 计算机科学, 2012, 39(12): 233-236.

Hu Yuwen, Xu Jiucheng, Sun Lin. Research on decision stability of evolution model of granular decision[J]. Computer Science, 2012, 39(12): 233-236.

[20] Gheorghe Pǎun. Membrane Computing[M]. Wuhan, China: Huazhong University of Science & Technology Press, 2012:2-4.

MembraneMembraneStructureofDecisionEvolutionSets

Hu Yuwen1,2,3, Xu Jiucheng1,2, Xu Tianhe1,2

(1．College of Computer and Information Engineering, Henan Normal University, Xinxiang, 453007, China； 2．Engineering Technology Research Center for Computing Intelligence & Data Mining, Xinxiang，453007, China；3．Library, Henan Normal University, Xinxiang，453007,China)

As a new research method for decision rules, decision evolution set is the theory to deal with evolution problems of decision rules in time series, which transfers the focus from static information system to dynamic time series and studies the time-dependent evolution regulations of decision information systems. At present, the evolution trace defined by normal structure of decision evolution set is a graph inn-dimensional space, which is difficult to describe. So the membrane structure is newly proposed in this paper to describe the decision evolution set. In the membrane structure, the reduced attributes are got attention in the same way. When the time goes from pointti-1to pointti, attributes will enter different membranes based on their influence to decision and the data flow made in the process will be labelled at the same time. Thereby the problem of evolution trajectory visualization for decision information system is then solved. And the evolution process and trace of decision evolution system has been demonstrated by using some samples.

rough sets； granular decision； decision evolution； membrane structure

国家自然科学基金(60873104, 61040037, 61370169)资助项目； 河南省科技攻关重点项目(112102210194)资助项目；河南省教育厅科学技术研究重点项目(13A520529)资助项目；河南省高等学校人文社会科学研究项目(2013-QN-371)资助项目；2013河南师范大学教育项目资助项目；河南师范大学青年科学基金(2014QK28)资助项目；河南省高等学校重点科研项目(16A520057)资助项目。

2015-05-20；

2015-09-08

TP18

A

胡玉文(1982-)，男，工程师，研究方向：粗糙集理论、粒计算和数据挖掘，E-mail:huyuwen611@qq.com。

徐久成(1963-)，男，博士，教授，研究方向：粗糙集理论、粒计算和数据挖掘，E-mail: xjch3701@sina.com。

徐天贺(1986-)，女，助教，研究方向：粗糙集理论、粒计算和数据挖掘，E-mail:tianhe1107@163.com。