基于聚类和核密度估计假设检验的异常值检测方法
周春蕾 田品卓 杨晨琛 王 皓
(1.南京大学计算机软件新技术国家重点实验室,南京,210023; 2.江苏方天电力技术有限公司,南京,211102)
基于聚类和核密度估计假设检验的异常值检测方法
周春蕾1,2田品卓1杨晨琛1,2王 皓1
(1.南京大学计算机软件新技术国家重点实验室,南京,210023; 2.江苏方天电力技术有限公司,南京,211102)
异常值检测是数据挖掘领域中的核心问题,在工业生产中也有着广泛的应用。准确高效的异常值检测方法能够及时反映出工业系统运行状态,为相关人员提供参考,而传统的异常值检测方法无法很好地检测出变化模式复杂、变化范围小、具有流数据特性的数据中的异常值。因此,本文提出了一种新的针对该类型数据的异常值检测方法:首先通过对数据进行聚类划分,将相似的数据进行归类,从而将原本复杂的数据分布拆解成为每个聚类下简单数据分布的叠加;然后使用核密度估计假设检验的方法对待检测数据进行异常值检测。在标准数据集和真实数据上的实验结果表明,该方法相比于传统的异常值检测方法在检测精度上有一定的提升。
异常值检测;聚类;假设检验;核密度估计
引 言
异常值检测是数据挖掘领域中的核心问题,近十几年得到了广泛的关注[1-3]。与此同时,异常值检测在金融诈骗检测[4]、抗网络入侵[5]和疾病诊断[6]等领域也有着非常广泛的应用。异常值检测主要关注如何甄别出数据集中不符合预期或不符合正常变化模式的异常数据点[7]。在检测完成后,可以通过数据预处理对异常值进行标注或剔除,获得不含噪声的数据,从而提升机器学习和数据挖掘算法的准确率。此外,检测到并输出的异常值也可为相关人员提供参考。
关于异常值的定义,Hawkins首先提出如果数据集中某个观察值与其他值有较大的偏差,则两者来源于不同的产生机制,该观察值为一个异常[8];Johnson等则认为异常值为数据集中一些表现模式和其他点不一致的数据点[9]。迄今为止,国内外学者提出了包括基于概率密度的异常值检测方法、基于距离的异常值检测方法、基于时间序列特性的异常值检测方法以及基于流数据的异常值检测方法等来对数据中可能存在的异常进行检测,如Barnett等[10]利用异常值往往出现概率很低的假设,使用多维高斯分布等方法来得到数据的概率密度函数,然后计算出数据出现的概率,将出现概率低的点标记为异常点。该方法的效果取决于能否精确地得到数据的概率密度函数,当数据分布很复杂,通过多维高斯分布拟合得到的概率密度函数和真实的概率密度函数存在很大差距时,该方法无法准确地得到异常值。Knorr等[11]利用异常值在数据空间中往往是一些孤立点,它们与正常点存在较远的距离,所在区域内数据密度很低的特性,使用k近邻算法来寻找小于一定距离的最近邻数量,如果近邻数量小于一定的阈值δ,就认为其为异常点。k近邻算法的时间复杂度为O(D*N),其中D为数据的维度,N为数据的样本数量。尽管该方法在寻找近邻点时可以采用Bentley提出的KD-Tree(K-dimensional tree)[12]树形数据结构将算法的时间复杂度减少到O(D*logN),但仍然无法有效地处理维度较高、数据量较大的数据。Breunig等[13]利用聚类算法将数据进行聚类,认为数量较小的类是异常类,然后衡量数据点的局部异常值因子(Local outlier factor, LOF)来判断其是否为异常点。LOF值实际反映的是样本点所在区域的样本密度与该点近邻所在区域的样本密度之间的关系,而在数量大、数据变化范围小及每个点所在区域的数据密度都比较大的情况下,各个点的LOF值将非常接近,因此无法精确得到异常点。苏卫星等[14]利用时间序列的变化在时间上具有延续性,所以异常值往往是一些剧烈变化、不符合之前时间序列变化特性的数据点的假设,使用自回归模型(Auto regressive,AR)来对数据进行预测,通过分析预测的残差结果是否有非常剧烈的变化来进行异常值的判断。贺力克等[15]通过对时间序列进行窗口划分,根据前后窗口内时间序列的各种统计量特征来判断时间序列是否发生突变或者跳变,从而确定是否存在异常值。由于基于时间序列的异常值检测方法已存在前提假设,这类方法对于数据中存在的跳变异常点能够进行很好的识别,但是却无法准确地识别出渐变的异常点。Moradi等[16]使用滑动窗口的方法对窗口内的数据进行异常值检测,对每个待检测窗口中的数据,使用K-Means++方法进行聚类,聚类后数据量较少的类中的点即被认为是异常点。该方法只利用了当前窗口内的数据信息,能够检测出不符合当前窗口中的数据变化规律的异常值,但是无法检测出全局的异常值。
此外,当存在异常值标注时,可以利用一些监督方法对异常值进行检测,例如Ngan等[17]利用正常数据训练一个单类支持向量机来对数据点进行分类;Pawlowski等[18]利用贝叶斯网络进行异常值判断。而对具有特定结构信息的数据,也存在针对图结构的[19]和针对高维数据的异常值检测方法[20]等,由于篇幅所限,在此不做具体讨论。
针对变化模式复杂、变化范围很小、有时间序列特性的流数据异常值检测,本文提出了一种基于聚类和核密度估计(Kernel density estimation,KDE)[21]假设检验的异常值检测方法。该方法利用正常数据是由多个简单概率函数叠加而成的假设。首先采用基于层次方法的平衡迭代规约和聚类(Balanced iterative reducing and clustering using hierarchies,BIRCH)[22]算法对数据进行划分,将正常数据中相似的、具有相同变化规律的数据划分到同一类中,从而将原始复杂的数据分布简化为多个简单数据分布的叠加;然后在每个类中使用核密度估计假设检验的方法,对待检测样本进行异常值检测。实验结果表明,该方法相比基于高斯分布、基于时间序列和基于流数据的异常值检测方法,具有更高的精度,能够更好地检测出该类型数据中的异常点和工业生产中传感器产生的变化模式复杂的流数据中的异常值。
1 无监督流数据异常值检测
针对具有变化模式复杂、变化范围很小、有时间序列特性的流数据异常值检测问题,需要在无监督的情况下,从大量的历史数据中找出与正常的数据变化模式或者数据分布不同的数据点。该问题可以形式化表述为:给定一串具有时间序列特性的数据D={x1,x2,…,xn},xi∈D为一个d维数据,异常值检测就是从中找出不符合数据变化规律和变化模式的异常点Do={o1,o2,…,ok},其中k≪n,Do⊂D。
判断一个点是否为异常点,一种常用的方法是将其转化为判断该点出现的概率是否足够大。如果出现概率大于一个阈值,那么该点可以认为是正常点,否则为异常点。如果该点出现的概率很难得到,可以通过判断它和正常数据是否服从同一分布来进行判断,如果该点和正常点来自同一分布就可以认为该点为正常点,否则为异常点。
定义1如果数据点xt出现的概率P(xt|x1,x2,…,xt-1)<δ,那么xt为异常点,否则为正常点。
定义2设fi(·)为{x1,x2,…,xt-1}服从的概率密度函数,如果数据点xt满足P(xt|fi(·))<δ,那么xt为异常点,否则即为正常点。
2 基于聚类和核密度估计假设检验的异常值检测方法

2.1 基于BIRCH的聚类划分方法
对变化模式复杂、变化范围很小、有时间序列特性的流数据进行聚类划分,可以根据相关参数将其相似的数据归为一类。根据数据特性,本文采用BIRCH算法和层次聚类算法实现数据划分。
BIRCH算法主要通过聚类特征(Clustering feature,CF)和聚类特征树(CF tree)来实现算法。CF代表一个聚类,每个CF向量都是一个三元组。对于一个记录数为N的d维聚类样本集X={X1,X2,…,XN},CF表示为CF=(N,LS,SS),其中LS为该聚类中所有样本的线性和,反映了聚类的质心;SS为该聚类中所有样本的平方和,反映了聚类的直径大小。聚类特征树由若干个CF向量构成,其结构类似于B-树。基于BIRCH的聚类划分算法如下,其中对于划分数量K,在具体应用中可通过设置不同值对数据进行测试,选择使算法性能最佳的值。
算法1基于BIRCH的聚类划分算法
输入:历史数据D,划分数量K
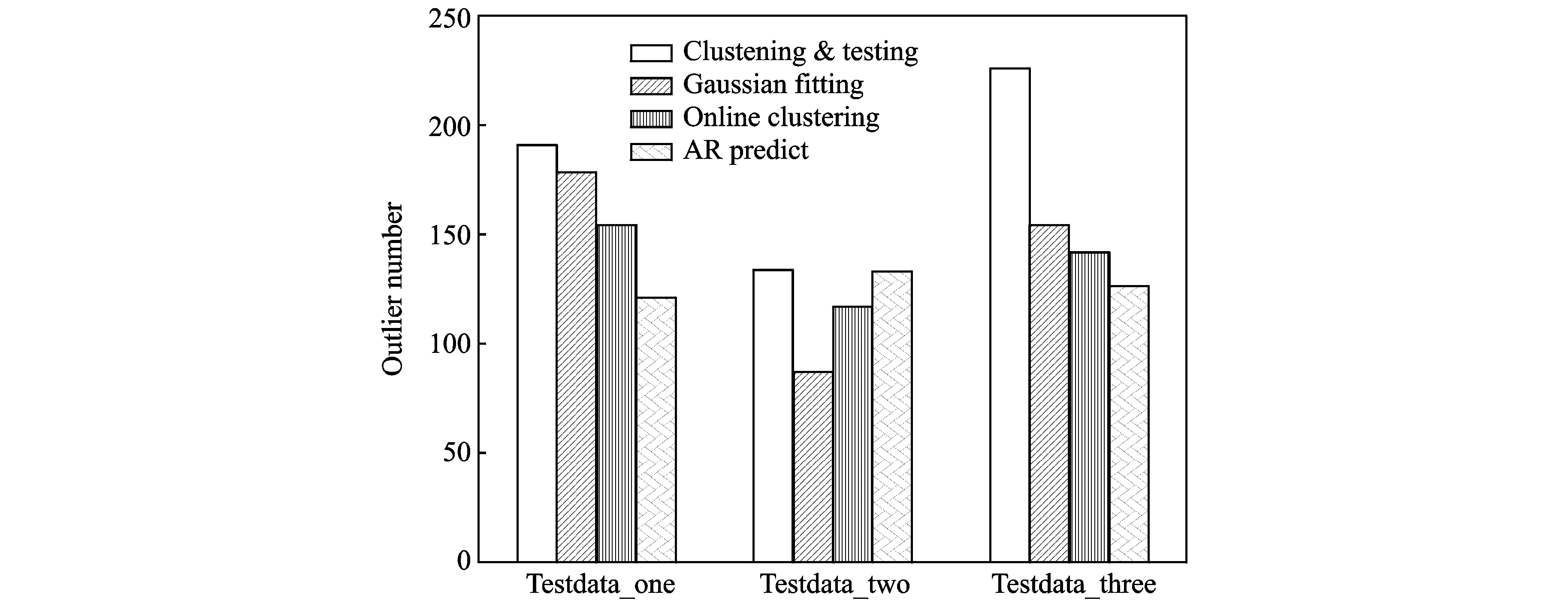
输出:{Di|0 (1)根据输入样本构建BIRCH算法中的CF tree; (2)对所有CF tree的叶子节点使用层次聚类算法进行全局聚类; (3)输出全局聚类结果作为划分结果。 在聚类划分完成后,使用核密度估计假设检验检测异常值,其主要思想是:对于每个子聚类中的数据使用核密度估计方法来得到数据的概率密度函数fj,其算法如下。但在数据量少的时候核密度估计方法无法很准确地反映出真实的数据分布,因此采用假设检验的方法来进行判断以得到更好的结果。 算法2核密度估计假设检验异常值检测算法 输入:待判断样本x,划分结果{Di|0 输出:0为正常点,1为异常点 (1)得到x所属划分Dj (2)if|Dj|>200:使用KDE核密度估计方法得到Dj的概率密度函数fj以及Fj,从而计算出x出现的概率P(x),如果P(x)<δ return (1); (3)else ifDj满足Shapiro-Wilk检验: 根据Dj内数据,计算得到μj和σj else return (1); (4)else ifx通过Mann-Whitney检验 return 0; else return (1)。 2.2.1 概率密度估计 KDE[21]是一种非参数估计方法,被用于估计未知密度函数。与参数估计方法不同的是,它无需假设数据服从某种分布,即可以在不利用任何先验条件的情况下,根据数据样本对未知密度函数进行估计,达到所估结果与真实结果间具有最小均方积分误差的目标。 假设x1,x2,…,xn为独立同分布F的n个样本点,设其概率密度为f,则其核密度函数估计为 (1) 式中h(h>0)为一平滑参数,可由Silverman拇指法则得到 (2) (3) 2.2.2 正态性检验-Shapiro-Wilk检验 虽然无参数的概率密度函数估计方法能够在对数据无任何先验知识的情况下得到较好的估计结果,但是这种方法是建立在大样本性质的前提上的。如果样本数量较少,得到的概率密度函数估计误差就会变大,因此它不适用于小样本即样本数小于200的情况。为了处理这种小样本情况,本方法采用Shapiro-Wilk检验[23]来确定样本是否服从正态分布。在满足正态性(通过W检验)的前提下,可以非常简单地得到数据出现的概率,从而判断其是否为异常值。 Shapiro-Wilk(夏皮洛-威尔克)检验也被称为W检验,建立在次序统计的基础上,其原假设H0为:总体服从正态分布。检验步骤为: (1) 将N个独立观察值按从小到大的次序排列,记为:x1,x2,…,xn。 (2) 依次将x1,x2,…,xn的值代入式(4)计算W检验统计量 (4) (3) 根据预先设定的显著水平α和样本容量N,查W检验统计量的P分位数ZP表从而得到统计量W的α分位数Wα。 (4) 作出判断:如果W 2.2.3 同分布检验-Mann-Whitney检验 对于不服从正态分布的样本,可以采用Mann-Whitney检验(U检验)[24]来判断两组样本数据是否来自于同一分布。 Mann-Whitney检验又称秩和检验,是一种用于比较两独立样本差异性的非参数检验方法。在检验时,首先将两组样本中的所有数据(假定两个样本总共有N个值)按从小到大的次序排列;再根据数值大小赋予每个值相应的的秩,其中最小值的秩为1,最大值的秩为N,而相同值的秩为各秩的平均值。若两样本之间的秩和差距较大,则计算U检验统计量后将拒绝原假设,认为二者之间存在明显差异,不可能来自于同一分布。其检验步骤为: (1) 混合两样本中的所有数据,根据数据次序赋予每个值相应的秩,其中最小值的秩为1,最大值的秩为混合后数据总数。若存在多个值相等的数据,则取各值秩的平均值作为该值的秩。 (2) 由(1)分别计算两样本所有数据的秩和W1和W2。 (3) 由(2)分别计算两样本所有数据的U检验统计量U1和U2,其中n1为样本1的数据总数,n2为样本2的数据总数 (4) 取U=min(U1,U2)作为最终统计量。 (5) 根据两样本数据总数n1,n2和置信水平α,查U检验表,获得U的临界值Uα。 (6) 对U和Uα的大小进行比较:若U 实验使用了UCI中的Activity recognition from a single chest-mounted accelerometer(ARFSCMA)数据集和一台燃煤机组超低排放数据两种数据。这两种数据集均具有时间序列特性,而且在某一段时间内数据变化范围不大,燃煤机组的超低排放数据相比于ARFSCMA数据的变化模式更为复杂。分别采用基于聚类核密度估计假设检验的方法、基于高斯拟合的方法[10]、基于AR时间序列的异常值检测方法[14]和基于流数据聚类的异常值检测方法[16]对测试数据进行异常值检测。 ARFSCMA数据集使用Single chest-mounted accelerometer记录了15位实验者在不同时间段内做7种不同动作时的值。分别选取其中的第1位和第2位实验者做第1个动作时的数据进行实验,因此该数据变化模式相对单一。使用4万条数据作为训练集,对300条数据进行异常值检测。在每一位实验者待检测的300条数据中,有200个异常值,其中包含渐变异常点和不同跳变程度的跳变异常点。把第1位实验者的待检测数据称为测试集1,第2位实验者的待检测数据称为数据集2。表1给出了4种不同的异常值检测方法在测试集1和测试集2上的测试结果。 表1 4种异常值检测方法在ARFSCMA数据集上的检测结果 Tab.1 Detection results on ARFSCMA data set by using four outlier detection methods 数据集聚类核密度估计假设检验高斯分布拟合流数据聚类AR时间序列预测测试集1191178154121测试集213487117133 使用一台装机容量为300MW的燃煤机组(以下称为测试机组)2016年5月除测试集之外的脱硫超低排放设施运行数据(1 min/条)为样本建立模型,其变化模式相对ARFSCMA数据更加复杂。以2016/5/31 15:40-2016/5/31 23:59共500条数据为测试样本,使用二氧化硫排放浓度为目标测点,检测二氧化硫时序数据中的异常值。测试样本中一共有250个异常值,其中包括渐变异常点和不同跳变程度的跳变异常点。 在检测过程中,对于BIRCH算法中划分数量这一参数,通过对样本数据测试不同值发现,当其为10时算法的性能最好,因此将划分数量设为10。在使用基于核密度假设检验的异值检测算法时δ=0.05,通过Shaprio-Wilk和Mann-Whitney检验的置信度为95%。把真实工业数据的测试样本称为测试集3,表2给出了4种异常值检测方法在真实工业数据上的检测结果。 表2 4种异常值检测方法在真实工业数据上的检测结果 Tab.2 Detection results on real industrial data by using four outlier detection methods 数据集聚类核密度估计假设检验高斯分布拟合流数据聚类AR时间序列预测测试集3226154142126 图1为4种异常值检测方法在3种不同数据集上的检测性能比较结果,其中testdata_one到testdata_three分别代表测试集1到3。Clustering & testing代表本文的方法,Gaussian fitting为高斯分布拟合方法,Online clustering为流数据聚类方法,AR predict为基于AR预测的时间序列异常值检测方法。从图1可以看出,相比于其他3种方法,基于聚类和核密度估计假设检验的方法在标准数据集和真实的工业数据集上都取得了比较好的效果,而且都能够检测出大部分的异常点。特别是在甄别机组超低排放数据这种变化模式比较复杂的实际应用环境中,本文提出的方法相比于其他3种方法,优势更加明显,能够检测出90%的异常。 图1 4种异常值检测方法在3种不同数据上的性能比较Fig. 1 Performance comparison of four outlier detection methods on three datasets 异常值检测在工业生产中有着广泛的应用,但异常值检测算法往往需要针对不同的数据特点和应用场景进行设计。本文针对变化模式复杂、变化范围很小和有时间序列特性的流数据,提出了一种基于聚类和KDE假设检验异常值检测方法。该方法充分利用大量的数据信息,合理选取聚类参数对数据进行聚类,从而对原始复杂的数据分布进行简化,能够更好地拟合得到数据的概率密度函数。同时,针对KDE算法在样本数量较少时会出现精度不高的情况,设计了一种基于假设检验的算法来进行处理,相比较单纯使用KDE,算法适用性得到了提升。该算法为变化模式复杂的燃煤机组超低排放数据异常值检测提供了一个普适的处理框架,相比于传统异常值检测算法,其准确率更高。下一步希望能够在分布式环境下处理该问题,使得算法性能和处理效率能够得到进一步的提升。 [1] Aggarwal C C. Outlier analysis[C]∥Data Mining. Switzerland: Springer International Publishing, 2015: 237-263. [2] Chandola V, Banerjee A, Kumar V. Anomaly detection: A survey[J]. ACM Computing Surveys (CSUR), 2009, 41(3): 15. [3] Hodge V, Austin J. A survey of outlier detection methodologies[J]. Artificial Intelligence Review, 2004, 22(2): 85-126. [4] Phua C, Lee V, Smith K, et al. A comprehensive survey of data mining-based fraud detection research[C]∥Artificial Intelligence Review. [S.l.]: Springer, 2005. [5] Kim G, Lee S, Kim S. A novel hybrid intrusion detection method integrating anomaly detection with misuse detection[J]. Expert Systems with Applications, 2014, 41(4): 1690-1700. [6] Schiff G D, Volk L A, Volodarskaya M, et al. Screening for medication errors using an outlier detection system[J]. Journal of the American Medical Informatics Association, 2017, 24(2):1-7. [7] Gupta M, Gao J, Aggarwal C C, et al. Outlier detection for temporal data: A survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(9): 2250-2267. [8] Hawkins D M. Identification of outliers[M]. London: Chapman and Hall, 1980. [9] Johnson R A, Wichern D W. Applied multivariate statistical analysis[M]. Upper Saddle River, NJ: Prentice Hall, 2002. [10] Barnett V, Lewis T. Outliers in statistical data[M]. Chichester, UK: John Wiley & Sons, 1994. [11] Knorr E M, Ng R T. A unified approach for mining outliers[C]∥Proceedings of the 1997 Conference of the Centre for Advanced Studies on Collaborative Research. Toronto, Ontario, Canada: IBM Press, 1997: 11. [12] Bentley J L. Multidimensional binary search trees used for associative searching[J]. Communications of the ACM, 1975, 18(9): 509-517. [13] Breunig M M, Kriegel H P, Ng R T, et al. LOF: Identifying density-based local outliers[C]∥ACM Sigmod Record. New York, NY, USA: ACM, 2000, 29(2): 93-104. [14] 苏卫星, 朱云龙, 胡琨元, 等. 基于模型的过程工业时间序列异常值检测方法[J]. 仪器仪表学报, 2012,33(9): 2080-2087. Su Weixing, Zhu Yunlong, Hu Kunyuan, et al.Model-based outlier detection method for time series of process industry[J]. Chinese Journal of Scientific Instrument,2012,33(9):2080-2087. [15] 贺力克, 聂平由. 时序数据故障点检测方法分析比较及应用[J]. 湖南师范大学自然科学学报, 2012, 35(2): 35-40. He Like, Nie Pingyou. Comparison and application of fault point detection method used in time series data analysis[J]. Journal of Natural Science of Hunan Normal University, 2012, 35(2): 35-40. [16] Moradi K H, Ibrahim S, Hosseinkhani J. Outlier detection in stream data by clustering method[J]. Social Science Electronic Publishing, 2014,2:25-34. [17] Ngan H Y T, Yung N H C, Yeh A G O. A comparative study of outlier detection for large-scale traffic data by one-class SVM and kernel density estimation[C]∥SPIE/IS & T Electronic Imaging. San Francisco, California, USA: International Society for Optics and Photonics, 2015: 94050I-1-94050I-10. [18] Pawlowski N, Jaques M, Glocker B. Efficient variational Bayesian neural network ensembles for outlier detection[C]∥The 5th International Conference on Learning Representations. Toulon, France: [s.n.], 2017. [19] Pincombe B. Anomaly detection in time series of graphs using ARMA processes[J]. Asor Bulletin, 2005, 24(4): 2. [20] Paulheim H. Identifying wrong links between datasets by multi-dimensional outlier detection[C]∥Proceedings of the Third International Workshop on Debugging Ontologies and Ontology Mappings. Greece: [s.n.],2014: 27-38. [21] Silverman B W. Density estimation for statistics and data analysis[M]. [S.l.]: CRC Rress, 1986. [22] Zhang T, Ramakrishnan R, Livny M. BIRCH: An efficient data clustering method for very large databases[C]∥ACM Sigmod Record. New York, NY, USA: ACM, 1996, 25(2): 103-114. [23] Shapiro S S, Wilk M B. An analysis of variance test for normality (complete samples)[J]. Biometrika, 1965, 52(3/4): 591-611. [24] Mann H B, Whitney D R. On a test of whether one of two random variables is stochastically larger than the other[J]. The Annals of Mathematical Statistics, 1947,18(1): 50-60. OutlierDetectionBasedonClusteringandKDEHypothesisTesting Zhou Chunlei1,2, Tian Pinzhuo1, Yang Chenchen1,2, Wang Hao1 (1.State Key Laboratory for Novel Software Technology, Nanjing University,Nanjing, 210023, China; 2.Jiangsu Frontier Electric Technology CO.LTD, Nanjing, 211102, China) Outlier detection is the core problem in data mining and is widely used in industrial production. Accurate and efficient outlier detection method can reflect the condition of industrial system in time, which provides reference for the relevant personnel. Traditional outlier detection algorithms can′t efficiently detect outliers in those data with complicated change modes, small change range and the characteristics of streaming data. In this paper a new method for detecting outliers is proposed. Firstly, the data are clustered into several categories by clustering. The data in the same categories share the common characteristics. In this way, we believe that the data in the same categories are under the same distribution which are simpler to fit than the whole data. So the original complex data distribution can be factored into several simple distributions. Secondly, kernel density estimation (KDE) hypothesis testing is used for abnormal value detection. Experiments in the UCI dataset and real industrial data show that the proposed method is more efficient than traditional methods. outlier detection; clustering; hypothesis testing; kernel density estimation 国家自然科学基金(61503178)资助项目;江苏省自然科学基金(BK20150587)资助项目。 2017-05-18; 2017-07-09 TP391 A 周春蕾(1973-),女,工程师,研究方向:电力行业节能减排信息化,E-mail:13851845492@163.com。 王皓(1983-),通信作者,男,博士,研究方向:数据管理、机器学习,E-mail: wanghao@nju.edu.cn。 田品卓(1991-),男,硕士,研究方向:机器学习,E-mail:tianpinzhuo@qq.com。 杨晨琛(1990-),女,助理工程师,研究方向:电力行业节能减排技术,E-mail:15951854315@163.com。2.2 核密度估计假设检验的异常值检测方法



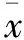
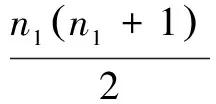
3 实验结果
3.1 UCI数据集结果

3.2 真实工业数据

3.3 实验结果分析
4 结束语





