美国防洪减灾的风险分析与Monte Carlo计算机数值模拟技术研究

刘文宁，李运辉

（水利部交通运输部国家能源局 南京水利科学研究院，江苏 南京 210029）

美国防洪减灾的风险分析与Monte Carlo计算机数值模拟技术研究

刘文宁，李运辉

（水利部交通运输部国家能源局 南京水利科学研究院，江苏 南京 210029）

近年来，由于全球气候变暖以及我国快速城镇化进程等因素，引起我国洪灾频发，造成国家生命财产巨大损失，因此，加强防洪风险分析技术迫在眉睫。文章通过对美国陆军工程兵团防洪减灾的风险分析系统的因素分析、自然变量与不确定性模型以及Monte Carlo计算机数值模拟洪水不确定性风险分析系统等研究，提出了一种将洪水流量与水位评估中的不确定性与不同程度的洪水固有风险结合起来的技巧，这一方法值得在我国洪水管理区广泛地借鉴与采纳。

防洪；风险；分析模型；数值模拟技术；Monte Carlo系统

在我国快速城镇化进程中，城市地貌发生剧烈变化，加上全球气候变暖以及城市热岛效应等诸多因素导致城市洪涝频发，强降雨灾害日益凸现。逢大雨必涝，已成为中国城市的一种通病。因此，迫切需要从技术层面上解决防洪减灾系统薄弱的问题。本文对美国陆军工程兵团河流系统防洪减灾的风险分析与数值技术进行研究，以期为我国相关专家学者提供有益参考与借鉴。

1 美国洪灾风险系统的重要因素

河流系统洪灾风险取决于多学科因素，是由多学科（包括水文、水力与土工因素）多种运行可能造成的影响独立或综合起作用的。

在洪水风险的多种来源中，我国传统上仅通过洪水频率因素作随机考虑。该因素确实对洪水风险影响最大，通常超过破坏风险的50%。但其他几个因素也是显著的，应该定量说明。此外，甚至对于洪水—频率因素，常规的评价方法可能也不完善。因此，有必要依据不同河流系统的水文学与水力学等重要因素，对保护区域洪水起评估作用。

1.1 水文重要因素

包括沿流洪水的洪水频率、洪量与时间分布，其依次取决于融雪与/或降雨特征、流域的降雨—径流关系与河流网络特征。降雨因素包括降水的时空分布、降雨资料、样本代表的准确性与充分性以及分析或模拟方法。流域—河流因素包括湖、水库与湿地的蓄水量、土壤水分、雨水截留与土地利用等不确定性数据等。

1.2 材料与施工的重要因素

包括大坝与堤防所用材料类型与质量、在运行期与施工时影响大坝或堤防质量的热力与水分变化以及施工质量控制等。

1.3 其他地球物理的重要因素

包括河流中冰的作用与冰对大坝、堤防或其他建筑物的作用、大坝、堤防或其他设施溃决引起的洪水暴发、闪电破坏以及龙卷风与其他天气影响等。

1.4 运行与维护的重要因素

包括洪水前和洪水期分水与泄水的操作方法、突发事件发生时的操作方法、河流系统安全检查、洪水期船只通行与捕鱼规定、修复与维护准则、放牧与其他土地使用以及植被覆盖与类型等。

1.5 水力的重要因素

包括河渠洪水传播特性与模拟洪水传播的公式与方法，其取决于河渠几何形状、河床糙率与坡度以及洪泛区的特性。还包括流域中水工建筑物的影响，如大坝与溢洪道、堤防、船闸、堰、水闸、闸门、阀、桥梁、取水口以及其他分流建筑物，还应包括河流泥沙的影响，如河槽的侵蚀、冲刷以及淤积，同时应考虑风与波浪的影响等。

1.6 结构与土工的重要因素

包括基础地质特性、堤防下的渗流和截渗、堤防材料内部侵蚀或管涌、填土或地下岩石强度不稳、远离堤防的深渗流破坏以及其他土力学问题等。

1.7 抗震的重要因素（大坝与堤防）

包括地震频率与大小、断层与构造特性、地震引起的坝址与堤防以及地基土液化、地震引起的大坝或堤防溃决相关的洪水年鉴概率等。

2 美国陆军工程师兵团洪水分析7个阶段

利用风险分析研究洪水大小由来已久。多年前美国学者Gumbel利用20世纪20年代开发的考虑极端事件分布的统计理论建立了洪水大小与其可能的重现期之间的关系。在20世纪50年代美国陆军工程兵团（以下简称兵团）定义了确定洪水—频率曲线的标准方法[2]。1968年美国国家洪水保险法的通过建立了国家洪水保险纲要（National Flood Insurance Program，NFIP），也导致了确定洪水频率曲线方法的综合研究时期。1981年则以广泛使用的“Bulletin 17B”的出版达到顶峰。在同一时期的英国也进行了洪水频率类似的综合研究。虽然美国与英国研究中使用的方法不同，但它们自那以后都成了标准，且被其他国家都广泛地仿效。

一个正式的洪水风险分析应包含7个阶段[3]，即对每个研究的保护方案进行下述风险分析。（1）给定洪水特性级别进行概率破坏分析；（2）确定一种方法用于导致风险性的过程或事件；（3）确定每个过程或事件中的参数；（4）对每个参数进行不确定性分析；（5）联合多参数不确定性以得到系统破坏概率；（6）得到相关不确定性的洪水经济损失函数；（7）结合破坏概率与损失函数得出预期年损失。

3 自然变量与不确定性的分析模型

洪水灾害风险分析要求提出与自然变量有关的不确定性、工程或经济模型以及统计关系。概念模型以描述水文风险转化对水库运行变化、河水位与水库出流关系、堤防可靠性以及对堤防破坏的经济损失评估[4]如图1所示。该图基本代表了当前美国陆军工程兵团的分析模型框架。

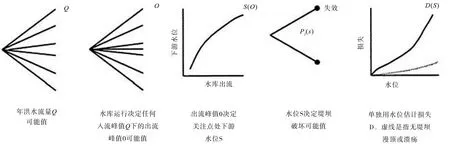
图1 描述洪水泄流转化为损失的模型概念

图1中的一些关系与自然变量有关。因为把这些方面处理为时间或空间的随机过程，它们可称为随机的。例如，年洪水水量的可能值就当作随时间不变的随机事件，与土工缺陷有关的堤防破坏部分地当作空间的随机事件。图1中的另一些关系与工程计算或函数规则有关。因为一个固定的因变量对应一个自变量的固定值，这些关系可称作确定性的。

对于图1中的每个阶段，都有一个将输入变量转换为输出变量的数学关系，每个关系都引出不确定性。一些不确定性来自自然变化，另一些来自工程计算，还有一些来自统计估计。对图1中模型概念的每个关系，都有一套参数用以确定相应公式或曲线。这些参数的值是不确定的。以模型概念的5个阶段来作说明：洪水—频率关系在左边（第一阶段），而水位—流量关系在中间（第三阶段）。

年洪水流量Q可能值是以概率分布表示的。假设这些洪水流为自然变量且可用概率来描述，这就要求一套参数来确定在流量轴向的形状与位置分布。使用的参数通常是流量对数的均值、方差以及偏态系数。另一方面，概率分布的形状与位置自身是不确定的，因此，洪水流量就涉及自然变异性与不确定性。

水位—流量关系常以回归公式表示[5]，这要求一套参数来描述水位—流量曲线关系的形状与位置。使用的参数通常是截距、斜率，也可是形状系数的某个形式。某种程度上，水位—流量关系反映了某段时间或在某河段内的自然变量（例如，水温、冲淤或支流水位引起的变化）。另一方面，可从有限的数据中估算回归公式。回归曲线的形状与位置本身是不确定的，作为洪水一频率曲线也有不完善性。因此水位—流量也涉及自然变异性与不确定性。最大的不确定性是对于罕见的极大的洪水。兵团的防洪减灾研究目标是确定可能的洪水引起的沿河断面期望年损失（EAD）用以比较作为工程方案函数损失变化。兵团计算的方法以洪水流量Q开始，Q等于或超过（平均而言）T年一遇洪水。T称为洪水流量Q的重现期。对应于重现期T是流量Q在任一给定年等于或超过的概率p。该年概率是重现期T的倒数，即

对于年概率p的某一洪水，相应的洪水损失D（p）的相应值能被估算。这是基于洪泛区淹没深度与被淹建筑物的价值。年期望损失是所有不同年超越概率下洪水与多年长期损失的平均值。它以数学公式表示为

当前兵团的方法将公式2的计算分为3步[6]（见图2）：确定洪水频率，用于描述等于或大于在某一给定时期内出现的某一流量Q（即水流体积）的洪水概率，如图2右上部所示；确定水位—流量关系，用于描述给定的水流流量下河段的水位高度，如图2左上部所示；确定损失—水位关系，用于描述某一给定水流高度下的损失量，如图2左下部所示。

图2中，逻辑关系是逆时钟转，起点是右上部，终点是右下。右下将年损失与概率p相关联。曲线下阴影区就是公式2给出的年期望损失。为了求出给定概率p下的损失，首先从图2右上部的洪水—频率曲线得到该概率下的流量QT。然后从图2左上部求得该流量下的水位高度（水面高程）H。根据H的值，可从图2左下部求出该水位高度下的损失D。通过将已知概率下损失绘于图右下部以及对一系列洪水概率重复如此的过程，就建立了损失—频率曲线。然后对该曲线积分以得出预期年损失。在美国陆军工程师兵团的方法中，年概率p=0.5，0.2，0.1，0.04，0.02，0.01，0.004与0.002是在计算中用到的值。

不确定性进入了分析计算的每一步中，从一步传到下一步，最终汇集到年期望损失，即任一给定年可能的损失的估算。损失估算的这些不确定性表述为损失的频率曲线，类似于洪水频率曲线，它描述给定时期（例如，年）超出给定大小洪水损失的概率。损失的频率曲线如图2右下部所示。兵团的概念方法利用洪水频率、水位—流量与损失—水位关系，模拟洪水灾害与相关损失，与长期的科学理解完全一致[7]。

4 Monte Carlo计算机数值模拟洪水不确定性风险

公式2中年期望损失（EAD）的确定考虑了可能发生的洪水大小范围，但它没有考虑损失计算中使用的水文、水力或经济信息的不确定性。如图2所示，传统方法没有告诉我们如何能确信计算的年期望损失超出预计。这是因为在年洪峰流量概率分布、洪量—洪水位关系以及洪水位—经济损失关系方面有很大不确定性。年期望损失的计算估值究竟有多准确？兵团洪水损失评估的新风险分析方法试图量化自然变异性与不确定性。

兵团运用Monte Carlo计算数值模拟风险分析方法提供了一个手段来估算年期望洪水损失的范围[8]。类似风险分析也能用于计算堤防溃决预期概率范围。考虑图2中右上角部分，一般来说，预期100年一遇的洪峰流量是相应的年概率p=0.01的流量。如何确保防护不同大小程度的洪水？如何防护100年或以上一遇小概率的所有洪水？风险分析提出了这样的问题。

假设作为风险分析能确定这种概率分布，就能把握可能破坏点超出洪峰流量概率不确定性（见图2右上部分），该函数的一部分如图3所示。比如，对100年一遇流量Q100提供90%把握的保护，这取决于估算的流量概率不确定性（见图3）、水位—流量关系以及堤防系统可靠性的概率。

3条曲线中最粗的表示从洪水频率分析得出的洪峰流量的预期概率。（其上下的两条细线分别定义了出超预期概率10%与90%置信界限。Q100表示被超越概率0.01的流量，而Q100+Δp表示90%置信100年一遇洪水不会超出该水平的流量。根据期望概率，该流量有被超越的0.01-Δp的概率。该方法与考虑水文分析和洪水频率评估中不确定性的安全系数相符）[9]。

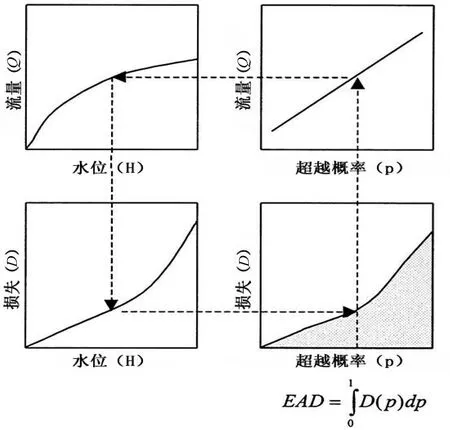
图2 兵团预期年损失（EAD）计算的原理

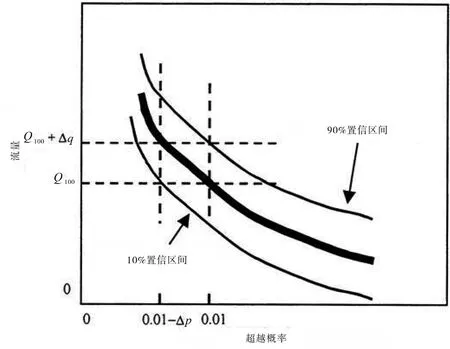
图3 概率分布

风险、不确定性与可变性是防洪减灾规划所固有的。河流洪水及由其导致的破坏的预测都有不确定性，只是因为我们不能充分了解对其起作用的所有因素。图2左下部水位—损失函数的不确定性包括：经济活动与经济条件或洪水期间洪泛区财产价值；预警时间与洪泛区居民的反应；洪水速度以及泥沙数量；恢复损失的财产所需时间。

图2左上部流量—水位函数的不确定性包括河道自然特性；在一定流速下可能影响洪水水位的风速；植被、沙石与其他障碍物包括河道中的冰。

图2右上部年峰值流量概率分布的不确定性包括统计估算水文曲线的有限数据；可能引发洪水的暴雨或其他事件（如上游大坝溃决，上游或下游堤防溃决）出现时间与严重程度；

可能洪水损失地的降雨排入渗历时与分布，以及在暴雨出现期间精确的降雨—径流与洪水演进过程（如流域地形、土地利用与覆盖物土壤含水率）；堤防与上游坝（结构的）溃决或操作（非结构的）破坏的可能性；洪水期间上游采取的保护当地的行动（临时措施）。

洪峰记录常用于估算某一给定或更大洪水发生的概率。但至少在两个环境下这样估算是不确定的。（1）用于估算水文曲线的历史洪峰观察次数受限（也许不准确）。（2）影响暴雨洪峰的下垫石特性的变化。大多数情况下，洪峰的概率分布是变化的，至少长期来看也多半不正确，即使确定降雨的概率特性没有变化。

f1(Q∣p)的点画线如图4所示，显示了一组3幅图描述流量、水位与损失不确定性。这些量的不确定性被概率分布与每条曲线周围的虚置信限线，以及每幅图中显示曲线可能的位置点画线表示。第一幅图显示了流量Q在某一概率p下的不确定性f1(Q∣p)。如果洪水—频率曲线是对数正态分布和近似如此的其他分布，不确定性f1(Q∣p)可采用偏态t分布更精确地给定。基于对数正态分布的洪水—频率曲线完全能被其均值与方差确定，所以如果均值与标准方差改变了，就能得到不同洪水—频率曲线。均值与方差的统计不确定性能被用于计算它们的大量数据来量化。利用Monte Carlo模拟生成不同的均值与方差，然后绘出洪水—频率曲线，这样，就能确定不同的洪水—频率曲线。

作为风险分析方法部分的流量（Q）、水位（H）与损失（D）关系的不确定性。（第一幅图表示流量与概率（p）的关系。实线是该关系最佳的估算值，而点画线表示实际曲线的一种可能情况。点线表明函数f1(Q∣p)可能的轮廓。这用于描述给定概率下流量不确定性的概率密度函数。第二幅图显示了流量与水面高度的关系（即特征曲线）。实线是该关系最佳的估算值，而点画线表示实际曲线假设的一种可能情况。函数f2(H∣Q)是给定流量下高度的概率密度函数。第三幅图表明损失与水面高度的关系。实线是该关系最佳的估算值，而点画线表示实际曲线假设的一种可能情况。函数f(D∣H)是给定水面高度下损失的概率密度函数[9]。

类似地，特征曲线或水位高度H与流量Q之间关系的不确定性可用图4中f2(H∣Q)曲线的概率分布与该图中点画线来表示。在此情况下，Monte Carlo分析仅运用单个随机变量在垂直方向上代替平均特征曲线。

最后，损失—水位函数的不确定性是用图4中f3(D∣H)曲线的概率分布来表示的点画线表示该曲线某种情况。该函数结合了不同种类不确定性的影响，包括堤防溃决的可能性、洪泛区建筑物高程的不确定性、一定淹没深度下建筑物受损程度知识的缺乏、财产与建筑物内价值的不确定性。

Monte Carlo模拟常用于更新图4中3条曲线。对于每组关系，如图2中描述的同样过程可求的转成预期年损失（EAD）值，好像每个数据是该曲线的真实值一样。换句话，对于每个概率区间dp，运用一个代表性的概率p*，由此从洪水—频率曲线可求得洪水流量Q*，进而从流量—水位曲线求得相应的水位高度H*以及从损失—水位函数求得导致的损失D*。通过在全概率轴上持续进行这一过程，然后利用公式2对该结果求积分，就可得出预期年损失。Monte Carlo模拟连续几千次循环生成数据并计算预期年损失，直到预期年损失值的统计值足够准确。Monte Carlo模拟形式比简单生成洪水并求得水位与损失，然后再生成新的洪水并求得水位与损失等的简单方法更成熟[10]。因此说，Monte Carlo模拟是利用随机数扰动关键变量的连接关系，而不是生成随机洪水并检验其后果。

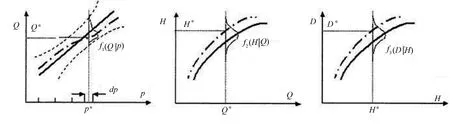
图4 f1(Q∣p)的点画线

5 结语

兵团方法中的计算程序利用Monte Carlo抽样对破坏河段进行损失概率曲线的数值积分。损失—概率函数从流量—概率、水位—流量以及损失—水位函数中求得。在此程序中，利用伪随机数单独来生成如下3个关系：流量—概率函数、水位—流量函数以及水位—损失函数，从而得以单独计算损失—概率曲线。再通过损失—概率曲线积分求得该情况下的年期望损失。该过程重复多次并取统计平均值。从统计的观点来看，通过增加如此计算次数，可使数值结果达到任意精度。

兵团的方法是合理先进的风险分析方法，它提出了一种将洪水流量与水位评估中的不确定性与不同程度的洪水固有风险结合起来的技巧，以给出该系统工程性能的总体风险度量。这一度量较常规使用的方法更为完善且在美国防洪体系中长期应用。这一方法值得我国考虑在洪水管理区广泛地借鉴与采纳。

[1] GUMBEL E J.The return period of flood fl ows[J].Annals of Mathematical Statistics，1941（2）：163-190.

[2] BEARD L R.Statistical methods in hydrology[M].Sacramento：Earlier Edition Published，1962.

[3] BROWN C A，GRAHAM W J.Assessing the threat to life from dam failure[J].Water Resources Bulletin，1988（24）：1303-1309.

[4] CALABRO S R.Reliability principles and practices[M].New York：McGraw-Hill，1962.

[5] CHOWDHURY J U，STEDINGER J R.Con fi dence intervals for design floods with estimated skew coef fi cient[J].Journal of Hydraulic Engineering，1991（7）：811-831.

[6] HAIMES Y Y. Risk modelling，assessment and management[M].New York：John Wiley，2008.

[7] CRESSIE N A.Statistics for spatial data[M].New York：John Wiley，1991.

[8] DAVIS D W.A risk and uncertainty based concept for sizing levee projects[A].In proceedings of a hydrology and hydraulics workshop on riverine levee freeboard[C].California：U.S. Army Corps of Engineers Hydrologic Engineering Center，1991：231-249.

[9] Institute of Hydrology.Flood estimation handbook[M].Walling for：Institute of Hydrology，1999.

[10] MOSER D A.The use of risk analysis by the U. S. army corps of engineers[A].In proceedings of a hydrology and hydraulics workshop on risk-based analysis. flood damage reduction studies[C].California：U.S. Army Corps of Engineers Hydrologic Engineering Center，1997.

Risk analysis and Monte Carlo numerical modelling techniques in mitigation of flood disasters in USA

Liu Wenning, Li Yunhui
（Nanjing Hydraulic Research Institute of Ministry of Water Resources, Ministry of Transport and National Energy Administration of the People’s Republic of China, Nanjing 210029, China）

In recent years, owing to global climate warming and Chinese rapid urbanization, flood disasters have been frequently induced and led to great losses of lives and properties in China. Therefore, strengthening the risk analysis techniques of flood control is urgent.In this paper, through researches on factors for risk analysis system, natural variables and uncertainty models as well as Monte Carlo numerical modelling uncertainty risk analysis system in flood reduction and disaster mitigation by USA Army Corps of Engineers, the technique coupling the uncertainty in evaluation of flood discharge and level with the inherent risks with different magnitudes of floods is proposed. The proposed method is worth to be referred and utilized in the flood management areas in China.

flood control; risk; analytic model; numerical modelling technique; Monte Carlo system

国家自然科学基金重点项目；项目名称：多因素协同作用下混凝土坝长效服役的理论与方法；项目编号：51139001。

刘文宁（1968— ），女，江苏南京人，工程师，学士；研究方向：水利工程运行与管理。