注重学科核心素养在教学中的落实——以高中数学为例

刘长伟

注重学科核心素养在教学中的落实
——以高中数学为例

刘长伟

学科核心素养的落实离不开一线教师的努力。高中数学教师应基于核心素养研究教材，构建具备问题、探究与反思的课堂，在教学中渗透数学思想，培养学生的理性精神。

数学核心素养；以人为本；理性精神

根据业内讨论，目前高中数学课程标准的修订专家倾向于将数学抽象、逻辑推理、数学建模、运算能力、直观想象、数据分析作为普通高中学生在高中数学学习过程中应该形成的六大核心素养。然而任何一项课程改革最终都会落实在课堂教学的实施上，如果一线教师不注重在课堂教学中的落实，再好的想法和指导意见都会变成空中楼阁。为此，笔者从培养学生核心素养的视角，谈谈自己在教学过程中的思考与实践。

一、基于核心素养研究教材

教材是一种资源，是我们教学的载体，它提供一个范本，指明了一个方向。因此在备课时对教材进行开发是一名教师必备的功课。新时期课改的基本理念是以学生发展为本，落实“立德树人”，培养和提高学生的数学核心素养。这就对教师备课又提出了新的要求，一定要以培养学生的核心素养为目标去重新审视教材，备好每一节课。

案例1：在球的体积公式的教学准备中，笔者参考了三个版本的教材，下面是三个版本教材中的片段。

湘教版高中数学必修3：教材直接呈现球的体积公式。设球的半径为r，则其体积为教材右边有一段独白：这个公式在以后学完微积分之后都会得到证明，现在同学们只要会用它们就行了。

苏教版高中数学必修2：运用类似求柱体、锥体的思想我们能够构造出一个重要的几何体，一个底面半径和高都等于R的圆柱，挖去一个以上底面为底面，下底面圆心为顶点的圆锥后，所得几何体的体积与一个半径为R的半球的体积相等，如图1，由此得到书的左边有一句旁白：做一个倒沙实验检验这一结果。

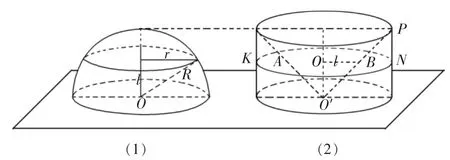
图1

如果从应试的角度来看，三个版本的教材所呈现的内容已经足够了，只要记住公式会用就可以了。而且三个版本的教材的旁白部分已经明确告诉教师和学生，要想知道为什么，以后会知道的，给想进一步在数学上有所造诣的学生留下了一个想象的空间。但如果从培养学生核心素养的角度来看，教师只照本宣科地教就毫无意义了。因此一定要进行再次备课，丰富教材的内容，笔者以为公式的教学，可以参照概念教学那样，让学生自己去发现、探究、归纳、概括、完善，构建出自己的知识体系，最终转化为学生数学素养的一部分。同时教师在教学过程中，要把自己对教材的理解、感悟、追求、教育智慧、创新精神及本人的人格魅力努力地展现出来去影响和感召学生，促进学生知识素养及精神素养的全面提高。笔者拟写备课提纲如下：

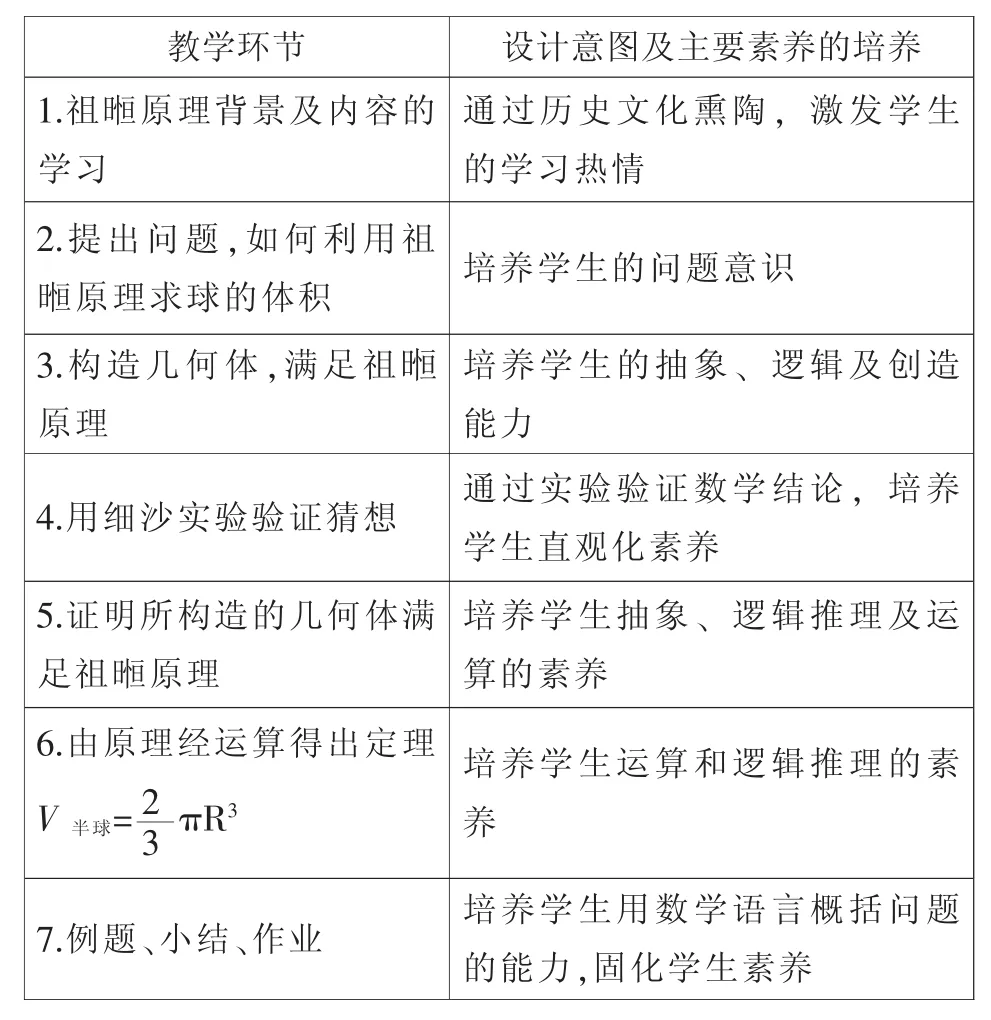
教学环节 设计意图及主要素养的培养1.祖暅原理背景及内容的学习通过历史文化熏陶，激发学生的学习热情2.提出问题，如何利用祖暅原理求球的体积 培养学生的问题意识3.构造几何体，满足祖暅原理培养学生的抽象、逻辑及创造能力4.用细沙实验验证猜想 通过实验验证数学结论，培养学生直观化素养5.证明所构造的几何体满足祖暅原理培养学生抽象、逻辑推理及运算的素养6.由原理经运算得出定理V 半球=2培养学生运算和逻辑推理的素养7.例题、小结、作业 培养学生用数学语言概括问题的能力，固化学生素养3πR3

以上教学提纲的设计显然不仅仅是在传授知识，而是通过知识的传授来培养学生的数学核心素养，比教材上所呈现的内容要丰富得多。

二、构建具备问题、探究与反思的课堂

课堂是教师教学的主阵地，教师的知识、技能、理念、风采都是在课堂上直接呈现在学生面前，因此课堂更是教师践行新课程理念的战场，培养学生的核心素养第一阵地就在我们教师平时的课堂上。笔者以为教师应该在课堂上注重对学生问题、探究与反思意识的引导。

案例2：圆锥曲线离心率问题的探究课的片段。

师：椭圆的离心率决定了它的“扁圆”程度，双曲线的离心率决定了它的“开口”大小。那么离心率对抛物线的形状有何影响？为什么所有抛物线的离心率都等于1？

学生1：老师，是不是任何抛物线的形状都是相同（即相似）的。

学生2（提出质疑）：抛物线的开口明显有大有小，形状怎么会相同呢？

教师引导学生回忆小学时学过的放大镜原理，放大镜是不能放大角度的，角经放大镜放大以后，这两条射线的粗细和长短被放大了，但角度仍旧不变。所以，放大镜只能把东西的各部分成比例地放大，而形状不变。 因此被放大镜放大后的图形和原图形是相似的。

师：下面就用我们都知道的放大镜原理研究一下抛物线的形状，我们以为例，在同一坐标系中画出的图像，通过实验观察y=x2的图像和的图像的关系，看结果怎样？

生：y=x2在4倍放大镜下观察得到的形状与的形状是相同的。

师：上面的问题只是我们直观及感性上的认识，对于一个数学命题仅仅这样还是远远不够的，还需要严谨的数学论证，下面我们就从理论上论证一下我们上面观察的事实。

（师生合作完成下面的证明）

以抛物线 y=ax2（a＞0）和 y=Ax2（A＞0）为例，证明它们是位似形，原点是位似中心。

设直线 OP的方程为y=mx（m＞0），直线 OP与抛物线 y=ax2（a＞0）的交点为 M，与抛物线 y=Ax2（A＞0）的交点 N，可以证出这是一个与直线OP无关的常数。因此，任何两个抛物线的形状都是相同的。

师（延伸与拓展）：由于圆锥曲线的渊源是相同的，也就决定了它们有许多相似的性质，那么，现在同学们能想到什么问题？

生3：对于椭圆和双曲线是不是也具有相同的性质？

师：你所提的问题正是老师要问的问题，那么就请同学们运用前面研究抛物线的经验，先研究一下椭圆吧。

经过分组讨论、分析、研究，得出结论：离心率相同的椭圆都是位似图形，即形状都相同。

师：同学们用同样的方法研究双曲线，把过程和结果记录在笔记上。

上面的教学过程，有提出问题过程、有探究问题过程，也有问题反思过程，学生完全参与其中，真正体现出学生是课堂的主人，教师只是他们学习的引领者、合作者。一节课从头到尾都能感受到学生学习的热情和对知识的渴求，这节课学生不但享受了解题过程的快乐，而且对圆锥曲线离心率的本质有了更深的理解。学生对离心率相同的圆锥曲线“形状都相同”这个和谐、美妙的结论感慨无比，体会到了数学之中的和谐之美。这些对学生的核心素养的培养是十分有意义的。

三、渗透数学思想，培养理性精神

数学思想是数学中的理性认识，因此中学数学强调数学思想的教学对学生理性精神的培养具有十分重要的意义。下面以函数的学习为例，试谈一下中学生对函数思想的认识。

高中对函数的学习是在初中函数学习的基础上进行的，内容分成了三个部分。苏教版的教材在必修1介绍了函数的概念及性质和几个初等函数，必修4学习了三角函数，选修2-1介绍了导数在函数中的应用。学习高中函数的定义，不免想起初中学习的函数定义，通过初高中函数定义的对比，在学完内容后要让学生真正地认识到，初中的函数定义告诉我们，世界上万物都在运动着，而且相互关联着，从某个数量的变化上看运动，便成为一个变量，而变量之间的关联，正是函数关系。到了高中，这时的函数，着重在一个集合的每一个元素到另一个集合中唯一确定元素之间的对应关系。高中函数的定义实际上是一种微观的考察，对初中的定义进行了抽象化、精确化的处理。动态的描述体现出一种文化内涵，粗略、生动、原始的思想，构成宏观的观念。静态的表述，则体现出形式化和精确化。数学研究除了要宏观地观察之外，还要深入地、细致地观察事物。世界万物都在变化之中，但只说事物在“变”，不说明什么问题，科学的任务是要找出“变化中不变化的规律”，上面我们提到过的函数的概念，函数研究变量之间的依赖关系，自然要谈变化。 但是只说变，而找不到一定的规律，就没有什么价值了。细细想来，不同的函数纵然千变万化但在变化之中总有一些保留的 “不变性”“规律性”，将之提炼出来，就是性质。比如函数的单调性、最值、周期性、奇偶性等性质就是变化中的不变性。 知道了函数性质，也就把握了函数变化的规律，掌握函数的知识，领悟了函数的思想。笔者以为学生在学习函数知识的过程中，能够体会和领悟到上述层次，才真正领悟了函数思想。

数学思想的形成非一日之功，数学思想的教学也不是一朝一夕就可以完成的，需要日积月累，长期渗透。由于数学思想的抽象程度较高，对它的掌握有一个从具体到抽象，从感性到理性，从低级到高级的过程。学生头脑中有了数学思想，才能逐渐形成数学素养，也才能达到课程目标中所提到的学会用数学眼光观察世界，学会用数学思维分析世界，学会用数学语言表达世界的要求了。

以上只是笔者的一点不成熟的想法，当然，要想真正贯彻执行好核心素养的教学，还有许多问题需要解决，还有很长的路要走。核心素养教育不论从理论上，还是实践上都是刚刚开始,相信基于核心素养的教学会越来越好。

［1］张奠宙.万变不离其宗：欣赏数学中的不变量与不变性质［J］.高中数学教与学，2012（01）.

［2］张奠宙，丁传松，柴俊.情真意切话数学［M］.北京：科学出版社，2011.

G633.6

A

1005-6009（2017）67-0037-03

刘长伟，江苏省苏州市高新区吴县中学（江苏苏州，215151）教师，高级教师。