基于RFM模型的半监督聚类算法①

程汝娇,徐鸿雁

(西南财经大学天府学院,绵阳 621000)

基于RFM模型的半监督聚类算法①

程汝娇,徐鸿雁

(西南财经大学天府学院,绵阳 621000)

客户分类作为客户关系管理(CRM)的重要管理方法,是企业进行市场营销的重要依据.通过对客户进行分类,有利于对客户价值进行准确评估,方便进行精准营销.本文通过对RFM模型数据集本身潜藏的先验结构化信息进行研究,标记出两组客户数据作为先验类别标记,进而得到两个初始聚类中心.基于传统K-means算法使用自适应方法确定K值和初始聚类中心.引入Must-link和Cannot-link两种约束将类别标记转换为成对约束信息,基于HMRF-KMeans成对约束,引入约束惩罚项和约束奖励项,实现对聚类引导和聚类结果的调整.使用改进的半监督聚类算法(RFM-SS-means)对标准数据集进行了测试,同时使用Food mart数据集对比了RFM-SS-means算法与传统K-means算法、two-steps算法的聚类效果.由实验结果可知,RFM-SS-means的CH系数最大,无需事先确定K值和初始聚类中心,聚类效果良好.

客户分类;半监督聚类;K-means;RFM模型

?

1 引言

随着信息科技的不断进步,企业经验与管理的理念不停在发生变化,企业营销经历了从“以产品为中心”到“以服务为中心”,再从“以服务为中心”到“以客户为中心”不断变迁[1,2].客户关系管理(Customer Relationship Management,CRM)成为最主流的“以客户为中心”的管理理念之一,适应企业发展的需求,近年来备受关注.客户分类作为CRM的重要管理工具,它是企业进行市场营销的重要依据[3-6].它对客户群体进行划分,方便确定高价值顾客,从而帮助企业重点关注高价值顾客群体[5].在众多的CRM的分析模式中,RFM模型备受瞩目,被各个不同领域广泛使用.RFM模型的参考变量是消费者消费行为的数据,不涉及客户私人隐私且容易得到,且此模型比较简单便捷,实践起来也比较有效.RFM模型是根据客户购买行为进行客户价值评估的模型,其通过 R(recency)、F(frequency)、M(monetary)三个变量,即最后一次购物时间R、某期间内的购买次数F以及某期间内客户花费总金额M来描述客户行为价值[7].传统的基于RFM模型的分类具有划分群组过多、消费的次数(F)和总金额(M)二者间有着共线性以及不同簇之间差距不大等缺点,近年来客户分类方法主要有K-means、Two-step及Kohonen神经网络算法等[8-12],这些算法往往自身存在不足,例如对初始聚类中心以及聚类数目的选取比较敏感、对离群点敏感、不适用于大数据等[9].其中,K-means是基于划分的算法,其运行速率较快且具有很高的运行效率,它的复杂程度为O(nkt),其中,n为数据库中实体数,t是迭代次数,k为簇的数目,一般来说,klt;lt;n,tlt;lt;n.K-means算法对大量数据集的处理,依然有着较高的效率和伸缩性,但划分数目K是K-means算法必要的输入的变量,它对运算结果影响较大且很难确定,随机确立的初始聚类中心也会导致大相径庭的甚至错误的聚类结果[13].同时,传统的聚类算法由于未考虑客户数据结构的特征,从而导致聚类过程存在盲目性.本文采用半监督聚类算法对客户分类展开研究,旨在减少或弥补上述客户分类算法的不足.

2 基于RFM模型的半监督聚类算法

半监督聚类算法是在聚类算法的基础上进行的,它的核心在于标记信息的处理以及标记信息与聚类算法的结合,即如何利用标记信息来控制或引导聚类的过程或者调整聚类结果,使得聚类结果最大程度上按照用户的意愿进行.

2.1 RFM模型客户数据集先验结构化信息

半监督聚类算法在实际应用中标记样本的方法主要有Wagstaff提出的Must-link和Cannot-link约束方法[14].假定给定数据集D,已知P、Q∈D,如果认为P、Q应当在同一类中,则Must-link(P,Q)=True,如果认为两者不应当在同一类中,则Cannot-link(P,Q)=True.Must-link和Cannot-link具有如下性质.

性质1.对称性.设D为数据集,P、Q∈D,则如下两式成立:

性质2.有限的传递性.设D为数据集,P、Q、R∈D,则下式成立:

Kotler作为客户营销战略的倡导者认为关系营销的重心要放在如何和最有价值的少部分顾客建立长期并为公司带来利润的关系[15],而Morgan和Hunt更明确指出顾客价值已经成为顾客关系营销的一个中心和重点[16],Wyner也指出企业80%的利润是来自于20%的顾客,而其余20%的利润,却花了公司80%的营销费用[17].

在进行RFM模型的客户数据结构分析时,我们可以发现该模型的三个评价R、F、M指标存在多重共线性,例如一个消费额大的客户通常消费频率较高,同时近期内有购买记录的可能性也较大.我们参考传统的RFM模型划分方式,将F、M两个影响因子从大到小排序,分别各选取前20%的两组客户数据集,然后再将R从近到远排序,选择前20%的客户数据集,这样我们就得到三组客户数据,然后筛选出在三组客户群组中都存在的客户,组成一个客户集D1.同理,将F、M两个影响因子从小到大排序,各选取前20%的两组客户数据,然后再将R从远到近排序,选择前20%的客户数据,这样我们就得到三组客户数据,然后筛选出在三组客户群组中都存在的客户,组成一个客户集合D2.

假设P1和Q1是属于D1中的任意两个数据,P2和Q2是属于D2中的任意两个数据,即P1、Q1∈D1,P2、Q2∈D2,则 Must-link(P1,Q1)=True,Must-link(P2,Q2)=True,Cannot-link(P1,P2)=True,Cannot-link(P1,Q2)=True,Cannot-link(P2,Q1)=True,Cannot-link(Q1,Q2)=True.通过计算可以得出集合D1和D2的Mustlink集合M和Cannot-link集合C.

2.2 成对约束

利用标记信息来控制或引导聚类的过程或者调整聚类结果的半监督聚类算法能使得聚类结果最大程度上按照用户的意愿进行,提高其效率和精度.HMRFKMeans[18]是近年来提出的一种半监督聚类算法,它基于马尔科夫随机场(Hidden Markov Random Field,HMRF)成对约束,目标函数为:

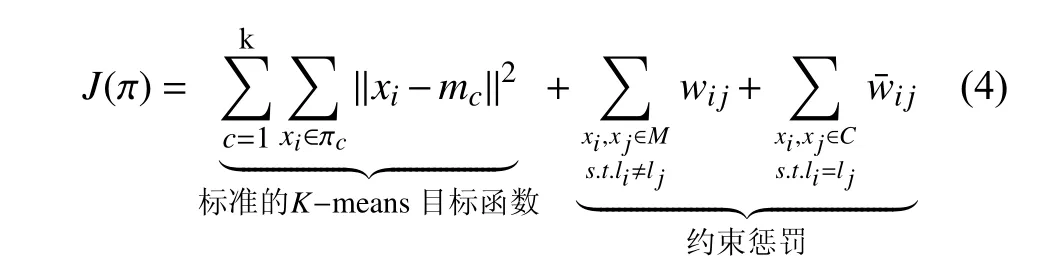
其中,M,C分别是给定的Must-link集合与Cannotlink集合;mc为聚类中心,wij,分别为违反Mustlink和Cannot-link约束规则的惩罚权重.在应用成对约束的半监督聚类方法中,满足li=lj的约束集合被称为Must-link集合.满足li≠lj的约束集合为称为Cannot-link集合.HMRF-KMeans算法使用欧式距离或余弦相似度计算权重.

2.3 自适应确定K值

基于传统K-means算法自适应确定K值的主要思想是:首先使用标记出的两组数据集,将该两组数据集的中值作为两个初始聚类中心;将剩余数据对象按照与这两个初始聚类中心的距离来划分类;然后将这些距离中距离聚类中心最远的点作为新的聚类中心,对所有的数据进行二次划分;如此循环反复,直到满足条件算法结束.基于传统K-means算法自适应生成K值的算法流程如图1所示.

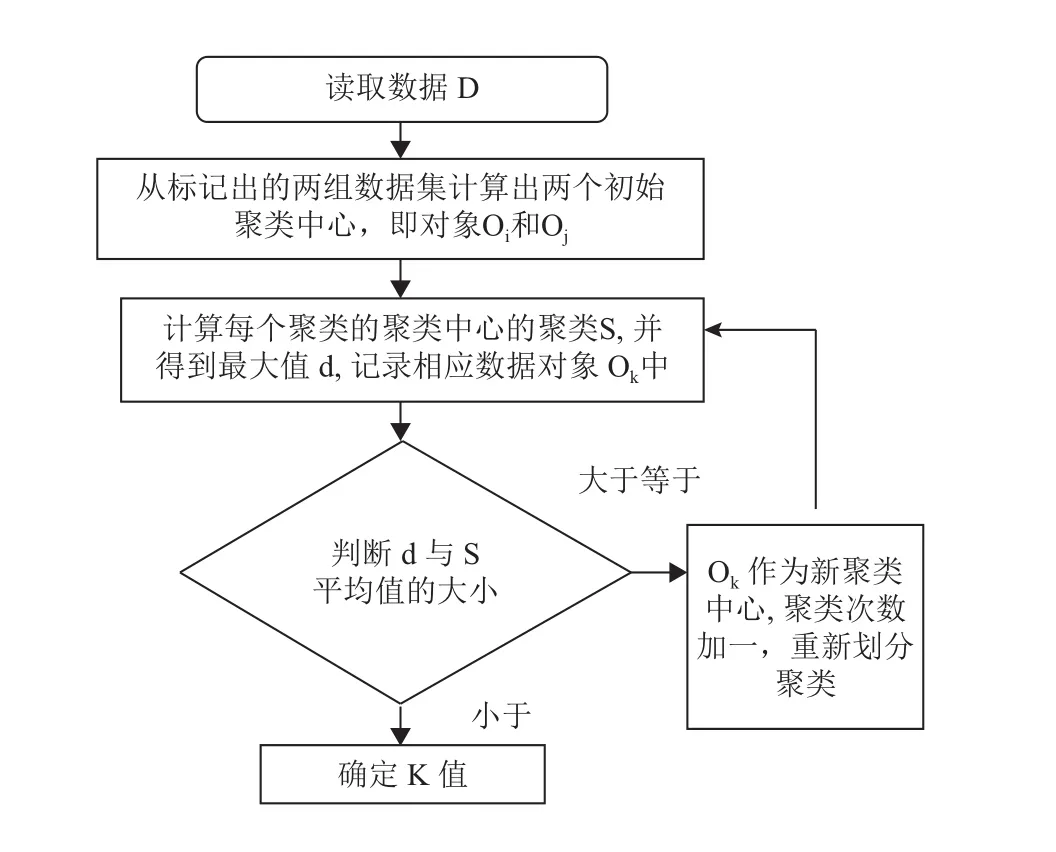
图1 自适应K值方法流程图

2.4 改进算法的实现

通过对RFM模型客户数据集先验结构化信息的处理,利用HMRF-KMeans成对约束思想和自适应确定传统K-means算法K值的方法,本文提出一种基于RFM模型的半监督聚类算法(Based on RFM model semi supervised K-means,RFM-SS-means),图2是改进后的算法总体流程图,其中虚线框内标明的是较传统K-means算法改进的地方.

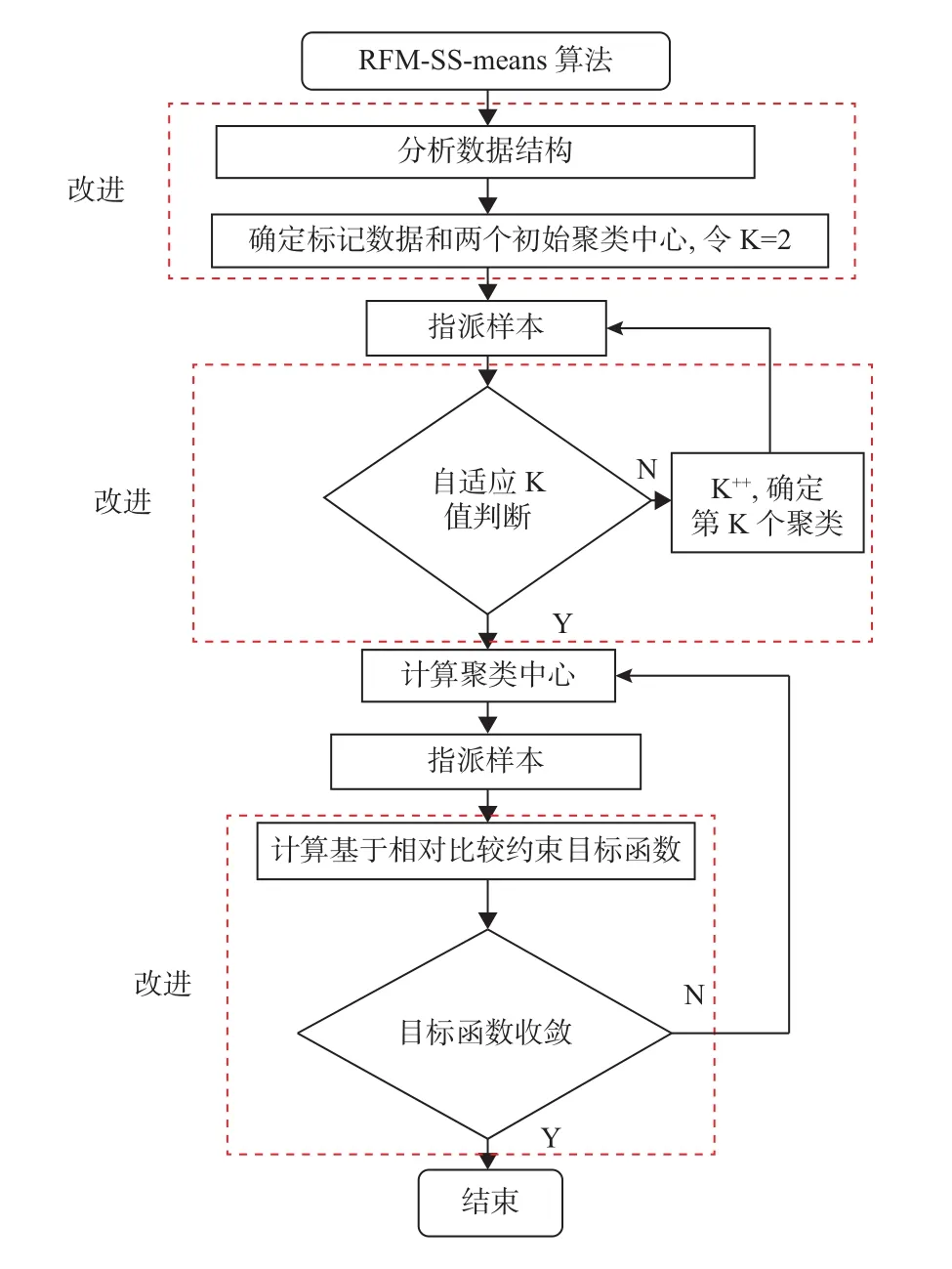
图2 改进的半监督聚类算法(RFM-SS-means)

RFM-SS-means算法挖掘了RFM数据集中本身潜藏的先验信息,使得聚类算法能够获取更多的启发式信息,从而减少了搜索过程的盲目性,使用标记数据选取初始聚类中心,避免了随机获取初始聚类中心导致的聚类结果的不稳定性,使用自适应确定K值的方法确定聚类数目,解决了聚类之前必须事先确立K值的不足.基于HMRF-KMeans成对约束,在传统的目标函数上引入约束惩罚项和约束奖励项,实现了对聚类引导和聚类结果的调整.

3 实验结果

3.1 标准数据集测试

UCI数据库(http://archive.ics.uci.edu/ml/)是一个国际上专业进行机器学习、数据挖掘算法测试的标准数据库.选择UCI数据库中的Iris和Wine这两个标准数据集作为测试数据集,测试RFM-SS-means算法聚类的准确性.

以数据集Iris为例,根据分类结果,选择Iris每个样本的三个属性(花萼长度、花萼宽度和花瓣长度)画出三维原始数据的分类效果图,实现可视化的目的,聚类效果如图3所示.

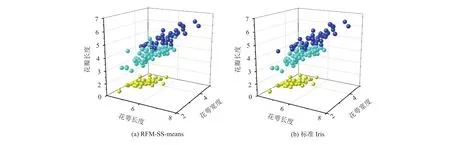
图3 RFM-SS-means算法与标准Iris的聚类效果

为了更加准确的检验聚类算法的性能,采用外部有效性评价指标FMI指标将聚类结果与“真实”聚类结果进行比较.随机选择Iris和Wine数据集中的15、30、45、60、75、90、105、130、145 个数据对象共18组数据,抽取数据对象时从每个类抽取同等数量的数据对象,进行准确性验证,得到结果如表1所示.

表1 RFM-SS-means算法的外部有效性评价结果

FMI指标结果区间为[0,1],值越大表示聚类效果越好,当FMI指标为1时,代表分类结果与“真实”分类情况完全一致.通过表1可以看出,RFM-SS-means算法在Iris数据集上的平均FMI指标达到了0.917,在Wine数据集上的FMI指标达到了0.719,具有较高的聚类准确性.

3.2 Food Mart数据库测试

考虑到UCI标准数据集并不具备RFM客户数据集的结构特征,难以发挥标记数据的作用,因此使用Food Mart数据集对改进算法进行测试.Food Mart数据库是根据某食品超市在1998年的售货记录得到的,该数据库RFM模型的基本特征.该数据库包含23张原始表,主要的数据表为sales_fact_1998(1998 年的商品交易数据),customer(顾客属性信息表,time_data(商品销售时间信息)等.顾客交易资料中关键字段解释如表2所示.

表2 Food Mart数据库字段字典

通过对Food Mart数据库中321个客户的相关客户信息、商品销售信息、商品销售时间等数据表进行处理,可以得到RFM模型的三个维度的输入变量:客户总消费(M)、消费次数(F)和最近消费时间间隔(R).运用本文前面提到的改进方法,对Food Mart数据库客户数据的先验结构化信息进行分析,可以得到两组消费行为迥异的用户族群,将这两组客户数据作为先验类别标记,进而可以得到RFM-SS-means算法的两个初始聚类中心.

分别应用K-means、two-step和RFM-SS-means算法对客户群体进行分类,根据三种聚类方法的分类结果,作出三维原始数据的客户分类效果图,如图4所示.

图4 三种聚类算法聚类效果图

为了准确的检验聚类算法的性能,采用内部检验法对三种方法的聚类结果进行效果评价,即分别计算出不同聚类结果的CH系数,得到如表3所示结果.

CH系数是基于对观测数据的组内距离差矩阵与组间距离差矩阵的测度,CH系数的值越大,则表明分类效果就越好.从表3可以得到Two-step、K-means与RFM-SS-means算法的CH系数分别为8.52,9.14,9.31,可以看出本文提出的半监督聚类算法聚类效果最优.

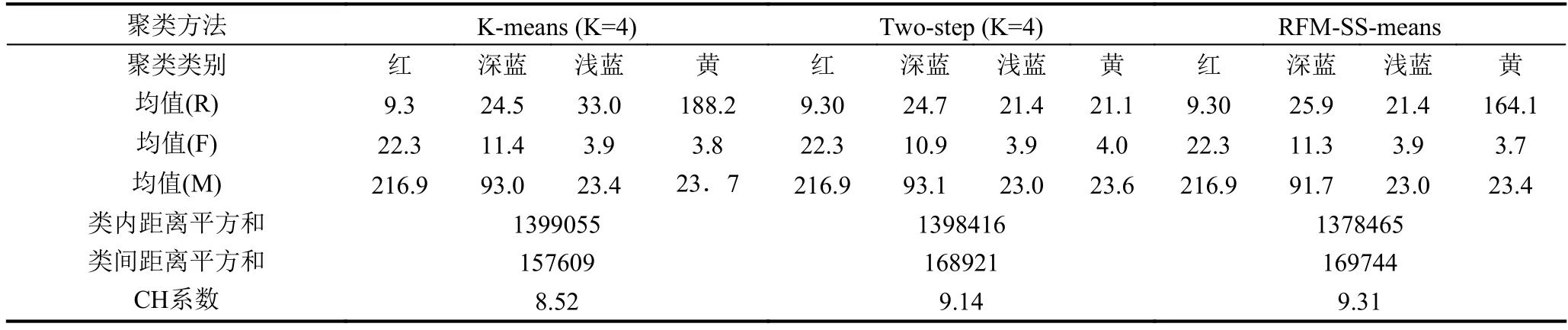
表3 不同聚类算法聚类效果的内部检验法评价(CH系数)

4 总结

本文提出了一种基于RFM模型和K-means算法的半监督聚类算法(RFM-SS-means).通过对客户数据集中本身潜藏的先验结构化信息进行研究,标记出两组客户数据作为类别标记,进而计算出两个初始聚类中心,同时采用自适应方法自动确定K值和初始聚类中心,解决了传统算法中K-means算法的K值和初始聚类中心难以确定的不足.引入Must-link和Cannotlink两种约束将类别标记转换为成对约束信息,基于HMRF-KMeans成对约束,在传统的目标函数上引入约束惩罚项,从而实现对聚类引导和聚类结果的调整,提高了聚类实现的效率.本文提出的RFM-SS-means算法可用于企业对客户群体的分类,有利于企业针对不同客户群体开展精准的营销活动,提高企业的营业收入和利润.

2 何荣勤.CRM原理·设计·实践.北京:电子工业出版社,2003:3–12.

3 Gloy BA,Akridge JT,Preckel PV.Customer lifetime value:An application in the rural petroleum market.Agribusiness,1997,13(3):335–347.[doi:10.1002/(ISSN)1520-6297]

4 马椿荣.消费者价值研究理论综述.商业时代,2014,(10):60–61.[doi:10.3969/j.issn.1002-5863.2014.10.025]

5 Hughes AM.Strategic database marketing:The masterplan for starting and managing a profitable,customer-based marketing program.Irwin Professional,1994.

6 Duboff RS.Marketing to maximize profitability.The Journal of Business Strategy,1992,13(6):10–13.[doi:10.1108/eb039521]

7 Cheng CH,Chen YS.Classifying the segmentation of customer value via RFM model and RS theory.Expert Systems with Application,2009,36(3):4176–4184.[doi:10.1016/j.eswa.2008.04.003]

8 徐翔斌,王佳强,涂欢,等.基于改进RFM模型的电子商务客户细分.计算机应用,2012,32(5):1439–1442.

9 闫相斌,李一军,叶强.基于购买行为的客户分类方法研究.计算机集成制造系统,2015,11(12):1769–1774.

10 郑茜茜.基于数据挖掘的客户细分研究[硕士学位论文].重庆:重庆交通大学,2013:8–10.

11 刘芝怡,陈功.基于改进K-means算法的RFAT客户细分研究.北京理工大学学报,2014,38(4):531–536.

12 潘玲玲,张育平,徐涛.核DBSCAN算法在民航客户细分中的应用.计算机工程,2012,38(10):70–73.[doi:10.3969/j.issn.1000-3428.2012.10.020]

13 张建萍,刘希玉.基于聚类分析的K-means算法研究及应用.计算机应用研究,2007,24(5):166–168.

14 Wagstaff K,Cardie C.Clustering with instance-level constraints.Proc.of the 17th International Conference on Machine Learning.San Francisco,CA,USA.2000.1103–1110.

15 Kotler P.Marketing management.Upper Saddle River,NJ:Prentice Hall,2000.

16 Morgan RM,Hunt SD.The commitment-trust theory of relationship marketing.Journal of Marketing,1994,58(3):20–38.[doi:10.2307/1252308]

17 Wyner GA.Customer valuation:Linking behavior and economics.Marketing Research,1996,8(2):36–38.

18 Basu S,Bilenko M,Mooney RJ.A probabilistic framework for semi-supervised clustering.Proc.of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York,NY,USA.2004.59–68.

Semi-Supervised Clustering Algorithm Based on RFM Model

CHENG Ru-Jiao,XU Hong-Yan
(Tianfu College of Southwest University of Finance and Economics,Mianyang 621000,China)

As an important management method of customer relationship management (CRM),the customer classification is the basis for enterprises to carry out marketing.The classification of customers is conducive to accurate assessment of customer value and facilitate the precise marketing.In this paper,we study the priori structured information hidden in the RFM model dataset,and mark two sets of customer data as a priori category mark,and then get two initial clustering centers.Based on the traditional K-means algorithm,the K value and the initial clustering center are determined with the adaptive method.Combining the two types of constraints of Must-link and Cannot-link,the category markers are transformed into pairs of constraint information.Based on HMRF-KMeans pairs,the constraints and constraint bonuses are introduced to improve the clustering guidance and clustering results.The improved semi-supervised clustering algorithm (RFM-SS-means)was used to test the standard data set,and the Food mart data set was also used to compare the RFM-SS-means algorithm with the traditional K-means algorithm and the two-steps algorithm Class effect.From the experimental results,it can be seen that the CH coefficient of RFM-SS-means is the largest,and the clustering effect is good without prior determination of K value and initial clustering center.

customer classification;semi-supervised clustering;K-means;RFM model

程汝娇,徐鸿雁.基于RFM模型的半监督聚类算法.计算机系统应用,2017,26(11):170–175.http://www.c-s-a.org.cn/1003-3254/6078.html

四川省高等教育改革项目([2014]156551)

2017-02-21;修改时间:2017-03-23;采用时间:2017-03-29

10.3969/j.issn.1007-3361.2007.11.031]

?