亚热带常绿阔叶林生物量模型及其分析

林开淼

（1. 戴云山国家自然保护区管理局，福建 德化 362500；2.福建师范大学 地理科学学院湿润亚热带山地生态重点实验室，福建 福州 350007)

亚热带常绿阔叶林生物量模型及其分析

林开淼1，2

（1. 戴云山国家自然保护区管理局，福建 德化 362500；2.福建师范大学 地理科学学院湿润亚热带山地生态重点实验室，福建 福州 350007)

缺乏阔叶树种生物量模型是影响亚热带常绿阔叶林生物碳库估测精度的重要原因，过去采用其他地区生物量模型估测亚热带常见阔叶林生物碳库，但其是否适用于本地区的阔叶林生物碳库估计仍存在争议。本研究在三明米槠林样地采用标准木结合相对生长方程法建立31株树的生物量模型，收集亚热带其他地区136株阔叶树生物量数据建立亚热带区域生物量模型，并与其他地区生物量模型比较。结果表明：亚热带区域阔叶林生物量模型为ln(AGB)=-1.982+1.209ln(D2)和ln(AGB)=-2.907+0.932ln(D2H)，树高和胸径关系模型为ln(H)=0.469+1.082ln(d)-0.106ln(D)2。Chave等建立的以胸径-树高为变量的湿润热带雨林生物量回归模型估算中亚热带森林生物量相对误差小于以胸径为变量建立的模型。Basuki、Brown、Chan、Ketterings和Kenzo等建立的生物量模型对我国中亚热带常绿阔叶林生物量估测精度不高，Ogawa的泰国常绿阔叶天然林生物量回归模型精度最高。该研究表明在利用区域生物量模型来估算中亚热带常绿阔叶林生物碳库应该检验其适用性，特别要考虑到模型的树种样本数量和胸径范围。

生物量模型；异速生长方程；阔叶林；生物碳库

亚热带常绿阔叶林是中国重要的碳汇林，科学精确估算亚热带常绿阔叶林的碳汇能力是我国森林碳汇功能研究的重要工作。目前森林群落的生物碳库估算方法主要有相对生长方程[1]、生物量-蓄积量方程[2]、生物量估算参数[3]、卫星遥感技术等[4]等。研究认为通过采伐样木建立相对生长方程，从而计算整个林分生物量，能够在小尺度上精确估算森林植被生物量[5]，然而其工作量极大、过程复杂、周期长等缺点，因此，建立具有代表性和科学规范的相对生长方程估算方法非常重要。近年来我国学者在常绿阔叶林生物量模型方面做了很多工作，在树种上主要对青冈Cyclobalanopsis glauca林、木荷Schima superba林、栲树Castanopsis fargesii林、桉树Eucalyptus robusta林等诸多常绿阔叶树种[6]，为这些林分生物量碳库估算提供了基础，而对以米槠为主要优势种的常绿阔叶林的研究还未见报道；在地域上主要集中在南亚热带和北亚热带常绿阔叶林生物量的研究[6-7]，对中亚热带的常绿阔叶林研究较少；而在林分类型上主要集中在常绿阔叶林次生林，而对老龄林的研究已见报道的只有南亚热带鼎湖山一例[8]。传统研究方法主要有皆伐法和相对生长法。皆伐法劳动量大，费工费时，十分繁杂，多数学者采用相对生长方程估算常绿阔叶林生物量。由于亚热带常绿阔叶林老龄林树种繁多，单树种的异速生长方程无法精确估计该地区森林生物量，因此，在估测亚热带常绿阔叶林生物量时，必须利用多树种的混合回归模型，才能更精确估计常绿阔叶林生物量。Waring等[9]研究结果表明多树种的混合回归模型可以利用代表性样地皆伐所获得的生物量数据如林分年龄、郁闭度、气象特征以及其他林分指标，也可以利用一定数量的单株生物量与胸径、树高、木材密度等测树因子建立回归模型，经过大量的研究发现后者在估测林分水平的生物量精确地更高，能够有效降低林分估测的不确定性[10]。因此，建立包含优势树种的多树种混合回归模型，有利于精确定量中亚热带地区常绿阔叶林老龄林生物量，为精确估计我国亚热带地区常绿阔叶林植被碳库提供支持。

为此本研究在福建三明格式栲自然保护区米槠常绿阔叶林区，采用标准木结合相对生长方程法建立以木荷、米槠、闽粤栲为优势种的区域特异混合异速生长生物量模型。并通过收集已经发表的文献资料，建立了亚热带地区总体异速生长生物量模型，并与热带亚热带地区区域性异速生长方程对比，分析两者在亚热带常绿阔叶林生物量估测的精确性，判断其是否能够适用于本地区的生物量碳库估算。

1 材料与方法

1.1 试验地概况

试验地位于福建省三明市格氏栲自然保护区内（26°19′N，117°36′E），区域内分布着大面积的常绿阔叶林，物种多样性丰富，该区域属于山地丘陵，地貌类型以低山、高丘为主，气候属于中亚热带季风气候，具有冬冷夏热、水热同季、湿润多雨的特点。全年气候温和，无霜期约350 d，年均气温20.3℃，年均降雨量1 530 mm，年均相对湿度79%，年日照时数1 706 h，海拔200～1 301 m。地带性土壤为山地红壤，成土母质为变质花岗岩。地带性植被多以米槠为主的常绿阔叶林，代表性的植物包括米槠，木荷，栲树等。

1.2 单株生物量的测定

本研究试验地位于福建省三明市格氏栲自然保 护 区 内（26°19′N，117°36′E）， 对 区 内 米 槠人促林乔木层生物量的测定采用相对生长法，于2011年11月选择米槠人促林树米槠、木荷、闽粤栲等主要组成树种和其他7个伴生树种树干解析和单株生物量测定[11]。

1.3 生物量回归模型拟合

采用的回归模型包括：

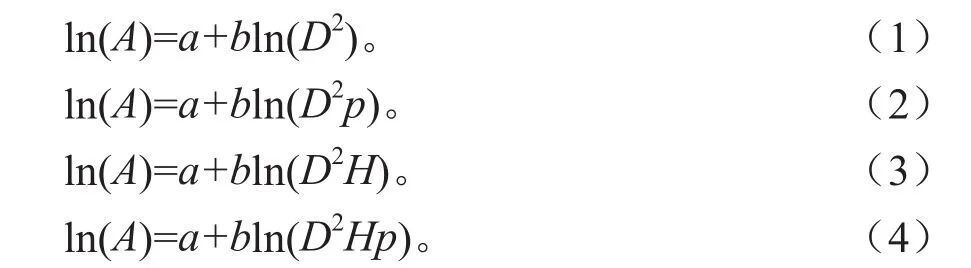
式中：A为地上部分生物量（kg）；D为胸径（cm）；H为高度（m）；p为密度（g·cm-3） 。

为建立亚热带地区常绿阔叶林通用生物量回归模型，收集亚热带不同地区常绿阔叶林植物生物量数据[6-8,12]，包括：杨同辉等[7]运用样方重叠和树干解析法测定了浙江天童木荷-米槠群落主要树种标准木41株数据，包括胸径和树高，胸径范围是1.5～45 cm；李根等[6]报道了南岭小坑流域具有典型群落结构的常绿阔叶林荷木群落、小红栲-荷木群落和藜蒴栲群落各树种的平均胸径、平均树高和地上部分平均生物量；温达志等[8]报道了南亚热带鼎湖山自然保护区内鼎湖山锥栗+黄果厚壳桂+荷木群落各胸径范围的平均胸径、平均树高和地上部分平均生物量，胸径范围2.31～122.2 cm；陈章和等[12]南亚热带粘木群落常绿阔叶林各胸径范围的平均胸径、平均树高和地上部分平均生物，胸径范围是5～65 cm。亚热带地区常绿阔叶林通用生物量回归模型的预测模型为模型1和模型3。

对胸径和树高的关系进行了检验，胸径和树高的关系采用的回归方程：

式中：H为树高（m），D为胸径（cm）。

所有的模型在进行回归模型预测前都进行了对数转换，对数转换解决了残差齐不齐问题，但是在估算生物量的时候也引入了误差[13]，因此，采用矫正系数CF进行矫正：CF= exp（RSE2/2），采用RSE为残差标准误[14]，RSE越小，预测精度越高。利用决定系数（R2）、akaike information criterion （AIC）[15]和平均偏差s（%）来评价方程的优劣。

式中：s为平均偏差，Yt是观测实际值，Yi是预测值，n观测数量。

1.4 与已发表的生物量回归模型比较

最优生物量回归模型（包括有树高和没树高变量）和已发表的热带和亚热带阔叶林生物量模型比较（表1）。为了检验各个模型的是否适用于中亚热带森林生物量预测以及预测精度，残差偏差RB和残差标准误RRMSE都被计算[16]：

其中，RRMSE为残差标准误越小预测精度越精确，RB为残差偏差；Yt是观测实际值，Yi是预测值，n观测数量。

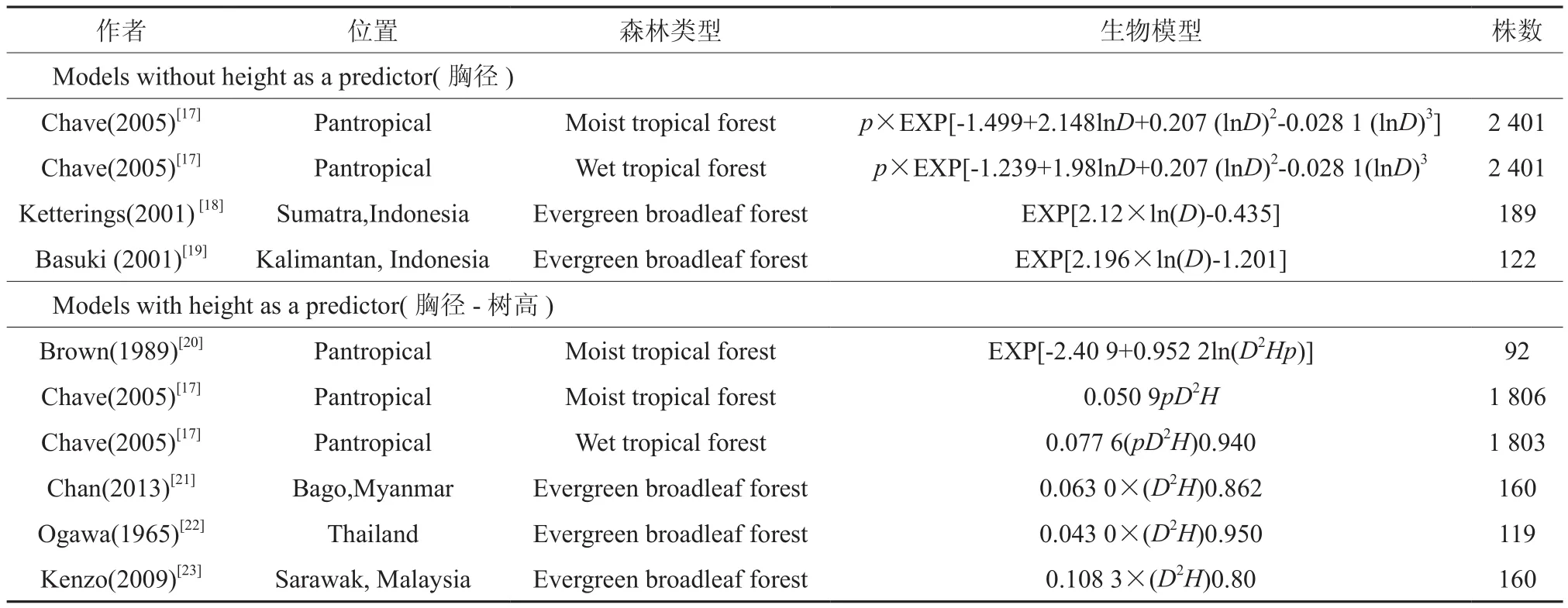
表1 热带和亚热带阔叶林生物量回归模型†Table 1 Biomass regression model of tropical and subtropical broad leaved forest

2 结果与分析

2.1 亚热带常绿阔叶林总体异速生长方程

亚热带森林区域生物量模型所用到的数据包括两类，一类是真实树种数据包括本实验地区的31株树和和浙江天童山41株树。另一类为平均木数据包括南亚热带粤北南岭小坑流域76株，南亚热带鼎湖山地区的19株。模拟的地上生物量模型见表2，其中以ln(AGB)=a+bln(D2)为最佳，其中R2为0.868，RSE为0.064，CF为1.002。而加入树高的异速生长方程ln(AGB)=a+bln(D2H)的精度较低，平均偏差最小为22.140。

表2 亚热带森林区域生物量回归模型Table 2 Biomass regression model of subtropical forest area

2.2 高度-胸径模型

生物量回归模型研究结果认为高度参数的引入能够显著提高生物量回归模型的精确度。为了分析高度-胸径之间的关系，通过收集的胸径和树高数据建立3个回归方程，结果见表3，二次型项ln(H)=a+bln(d)+cln(D)2能够最好的表示高度-胸径的关系，其中R2为0.846，RSE为0.016，平均偏差最小为8.270。

2.3 与其他回归模型比较

本文建立的以胸径（D2）、胸径-树高（D2H）为变量的亚热带常绿阔叶林地上部分生物量回归模型均能较好的预测研究地点的生物量，残差偏差RB分别为3.196和11.509，但是以胸径-树高（D2H）为变量的方程的预测精度较高（RRMSE较小）（见表4和图1 a，f）。在已经发表的10个热带和亚热带生物量估测回归模型中，胸径为变量生物量回归模型预测精度低于胸径-树高为变量。Chave等[17]的湿润热带雨林和湿热热带雨林通用生物量回归模型（见表4，图1 h，i）和Ogawa的泰国常绿阔叶天然林生物量回归模型（见表4，图1 k）能够最好的估算中亚热带地区常绿阔叶生物量，但以Ogawa预测的精度最高（RRMSE最小）[22]。而以胸径为变量的生物量回归模型Chave的湿润热带雨林通用生物量回归模型（见表4，图1 b）和Ketterings[18]在Indonesi地区的常绿阔叶天然林生物量回归模型（见表4，图1 d）预测精度较差。其他5个生物量模型不能作为预测亚热带常绿阔叶林的生物量模型，但是不同模型的偏差存在较大的差异。Chave等[17]以胸径为变量的湿润热带雨林生物量回归模型预测效果低估真实的生物量-26.480（见表4，图1 c）。Basuki的生物量回归模型胸径D＜30和D＞60cm的估算高于真实的生物量 25.698 （见表4,图1 e）[19]。Brown预测的生物量高于真实生物量22.492% （见表4，图1 g）[20]。Chan[21]和Kenzo[23]估测结果分别低于真实值的25.8和20.57%. （见表4，图1 j, l）。

预测模型包括2个亚热带常绿阔叶林异速生长方程通用模型和10个热带地区异速生长方程（见表4）

3 结论与讨论

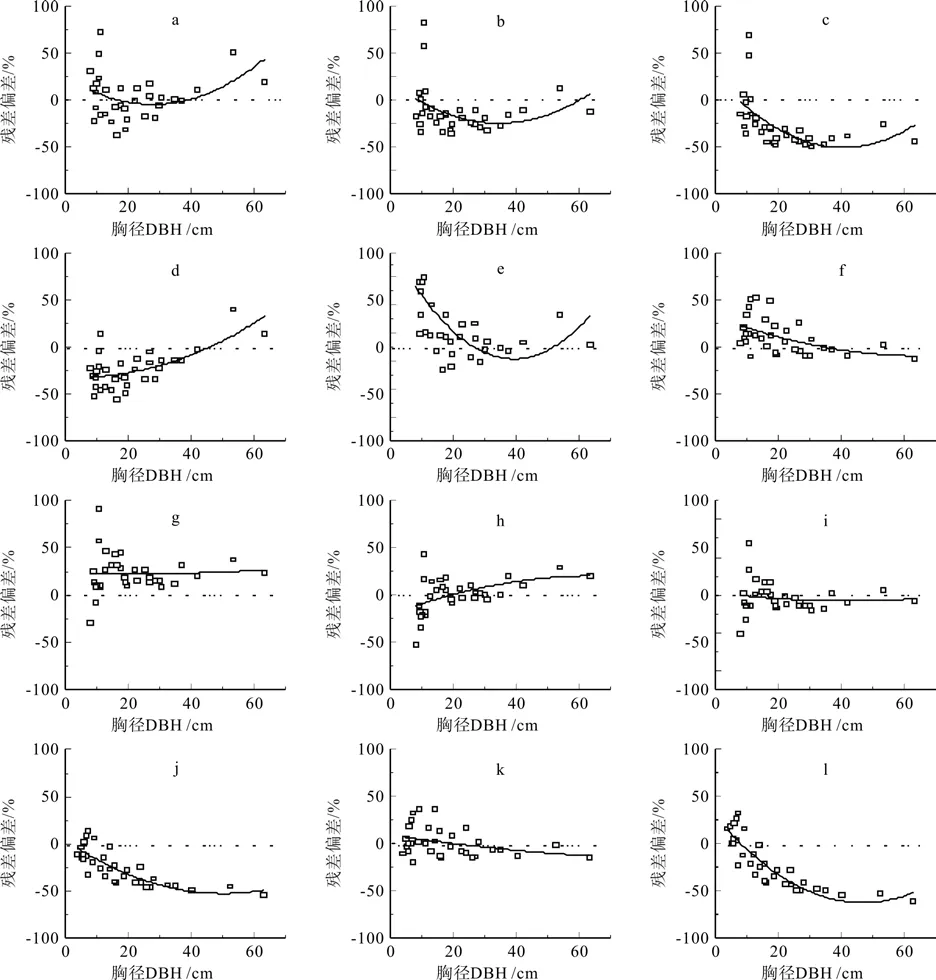
图1 亚热带常绿阔叶林31株树地上部分生物量预测误差Fig.1 Prediction error of aboveground biomass of 31 tree species in subtropical evergreen broad leaved forest

文章建立的亚热带区域森林生物量回归模型能够较好的估测常绿阔叶林的生物量。以胸径为自变量拟合的米槠人工林地上生物量回归模型能够较好的估算中亚热带地区米槠常绿阔叶林生物量，增加树高变量稍微提高估算精度。过去许多区域生物量回归模型都是以不同树种胸径、树高或密度为自变量拟合地上部分各器官生物量回归方程。Nelson等在亚马逊中部地区建立132株树种混合异速生长方程，其中以胸径为唯一变量的平均相对误差达到19.8%，而胸径-树高为变量的平均相对误差稍微下降为17.7%，而胸径、树高和密度三者结合的拟合生物量模型平均相对误差为14%[24]。Overman等的研究也证实了这一点，胸径、树高和密度三者结合拟合的地上部分生物量模型能够提高混合异速生长方程预测精度[25]。本研究构建的以胸径为自变量的米槠人工林地上生物量模型拟合度较高，平均偏差较小，增加树高和密度自变量能够轻微改进预测效果。而增加密度对米槠人工林地上生物量模型估测精度影响不大，有研究认为同一树种生物量模型，增加木材密度变量对模型拟合度影响不大[17,20]。而本研究中生物量模型是以米槠为主，米槠最大胸径（67.4 cm）远大于他7个伴生树种的最大胸径（30.0 cm），因此增加密度变量对整个模型的影响不明显。

物种特异异速生长方程常用于估算特定地区的森林生物量，然而在一些地区由于缺少当地物种特异异速生长方程，常用混合树种方程代替。许多学者尝试建立一个大尺度的可以忽视区域差异的总体异速生长方程，目前建立的总体异速生长方程最多是热带雨林，特别是非洲热带雨林[14]。而亚洲地区热带雨林和亚热带常绿阔叶林的总体异速生长方程仍然缺乏，这限制了亚热带森林的生物量的估测。本研究收集了我国亚热带森林的生物量估算数据，尝试建立一个亚热带森林总体异速生长方程。国内已经有许多亚热带地区的生物量模型区域特异异速生长方程和物种特异异速生长方程，然而由于已出版的文献生物量模型数据没有统一的标准，缺乏数据的完整性。本研究的亚热带森林总体异速生长方程只收集到南亚热带和中亚热带的生物量数据，缺少北亚热带地区是数据，而且部分数据是平均标准木数据，缺少最原始的资料。因此本研究构建的亚热带森林总体异速生长方程的平均相对误差较高。

本研究构建的常绿阔叶林异速生长方程，并来估算本研究的31株生物量，其平均相对误差较低，可以较好的估算中亚热带生物量。与其他地区的生物量回归模型比较，Chave等[17]建立的热带雨林总体异速生长方程估算中亚热带森林生物量相对误差最小，可能是Chave的生物量模型数据最多，而且来自于不同地区，建立的异速生长方程具有较高的代表性。Ogawa等[22]在泰国常绿阔叶林与我国中亚热带地区常绿阔叶林气候处于同一个纬度线上，森林类型基本相似，因此建立的区域特异异速生长方程能够在本地区运用。另外，Chan等[21]和Kenzo等[23]建立的区域特异异速生长方程估测的生物量低于本研究地区的生物量，这可能是他们的区域特异异速生长方程主要是以小树为主，缺少大树。因此，在运用其他地区建立的森林生物量回归模型来估算中亚热带常绿阔叶林应该检验模型的适用性，特别是要考虑到模型的样本数量和模型参数的胸径范围，否则将将低估或者高估林分生物碳库，未来为了进一步提高该异速生长方程的适用范围和估测精度，应该增加阔叶树种和大胸径树的数量。

[1]曾伟生,姚顺彬,肖前辉.中国湿地松立木生物量方程的研建[J].中南林业科技大学学报,2015,35(1):8-13.

[2]Kauffman JB. Heider C, Norfolk J,et al.Carbon stocks of intact mangroves and carbon emissions arising from their conversion in the Dominican Republic[J]. Ecological Applications, 2014,24:518-527.

[3]Montes N, Gauquelin W, Badri V,et al. A non-destructive method for estimating above-ground forest biomass in threatened woodlands[J]. Forest ecology and Management,2000, 130:37-46.

[4]曾 晶,张晓丽.高分一号遥感影像下崂山林场林分生物量反演估算研究[J].中南林业科技大学学报,2016,36(1):46-51.

[5]Brandeis T J, Delancey B, Parresol B,et al. Development of equations for predicting Puerto Rican subtropical dry foests biomass and volume[J]. Forest Ecology and Management, 2006,233:133-142.

[6]李 根,周光益,吴仲民,等.南岭小坑木荷群落地上生物量[J].林业科学,2012,48(3):143-147.

[7]杨同辉,宋 坤,达良俊,等.中国东部木荷-米槠林的生物量和地上净初级生产力[J].中国科学(生命科学),2010,40(7):610-619.

[8]温达志,魏 平,孔国辉,等.鼎湖山锥栗+黄果厚壳桂+荷木群落生物量及其特征[J].生态学报,1997,27(5):47-54.

[9]Waring RH, Schlesinger WH. Forest ecosystems: Concepts and management[M].USA: Academic Press, 1985:556-569.

[10]FAO. Global forest resource assessment: progress towards sustainable forest management [M]. FAO Forestry Paper, 2005:147-149.

[11]林开淼.亚热带米槠人促林碳、氮、磷积累特征及土壤磷素有效性分级研究[D].福州:福建师范大学,2015.

[12]陈章和,张宏达,王伯荪,等.广东黑石顶常绿阔叶林生物量及其分配的研究[J].植物生态学与地植物学学报,1993,17(4):289-298.

[13]Parresol BR. Assessing tree and stand biomass: a review with examples and critical comparisons[J].Annals of Forest Science,1999,45:573-593.

[14]Djomo AN, Ibrahima A, Saborowski J,et al.Allometric equations for biomass estimations in Cameroon and pan moist tropical equations including biomass data from Africa[J]. Forest Ecology and Management,2010,260:1873-1885.

[15]Akaike H. A Bayesian analysis of the minimum AIC procedure[J].Annals of the Institute of Statistical Mathematics,1978,30: 9-14.

[16]Tedeschi LO. Assessment of the adequacy of mathematical models[J].Agr. Syst.,2006, 89(2-3): 225-247.

[17]Chave J, Andalo C, Brown S,et al.Tree allometry and improved estimation of carbon stocks and balance in tropical forests[J].Oecologia,2005,145, 87-99.

[18]Ketterings QM, Coe R, van Noordwijk M,et al.Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests[J]. Forest Ecology and Management,2001,146: 199-209.

[19]Basuki T, Van Laake P, Skidmore A,et al.Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests[J].Forest Ecology and Management, 2009,257: 1684-1694.

[20]Brown S, Lugo A. Aboveground biomass estimates for tropical moist forests of the Brazilian Amazon[J]. Interclencia, 1992,17(1):8-18.

[21]Chan N, Takeda S, Suzuki R,et al.Establishment of allometric models and estimation of biomass recovery of swidden cultivation fallows in mixed deciduous forests of the Bago Mountains,Myanmar[J].Forest Ecology and Management,2013,304:427-436.

[22]Ogawa H, Yoda K, Ogino K, Kira T. Comparative ecological studies on three main types of forest vegetation in Thailand. II.Plant biomass[J].Nature and life in Southeast Asia,1965,4: 49-80.

[23]Kenzo T, Furutani R, Hattori D,et al.Allometric equations for accurate estimation of above-ground biomass in logged-over tropical rainforests in Sarawak, Malaysia[J].Journal of Forest Research ,2009,14: 365-372.

[24]Nelson BW, Mesquita R, Pereira JL,et al.Allometric regressions for improved estimate of secondary forest biomass in the central Amazon[J].Forest Ecology and Management,1999,117:149-167.

[25]Overman JPM, Witte HJL, Saldarriaga JG. Evaluation of regression models for above-ground biomass determination in Amazon rainforest[J].Journal of Tropical Ecology, 1994, 10: 207-218.

Research and analysis on biomass allometric equations of subtropical broad-leaved forest

LIN Kaimiao1,2
(1. Dai-Yun-Shan National Nature Reserve Administration, Dehua 362500, Fujian, China;2. College of Geographical Science, Fujian Normal University, Fuzhou 350007, Fujian, China)

Few data on tree biomass allometric equations are the important reason for the biomass carbon inaccuracy estimation of midsubtropical broad-leaved forest. It was a genera approach on the estimation the biomass of mid-subtropical broad-leaved forest using the existing pan tropical/subtropical equation developed by other areas. But it has a dispute whether it can be estimated accurately the biomass carbon of mid-subtropical broad-leaved forest using pan tropical/subtropical equation. This study using a data set on aboveground biomass for 31 trees destructively measured atCastanopsis fargesiiforest in Sanming; then collected the data set on 136 tree biomass in subtropical broad-leaved forest, and developed the pansubtropical allometric equations; then assessed the validity of the pan-subtropical and ten existing equations. The results believed that the best fi tted aboveground biomass model were ln(AGB)=-1.982+1.209ln(D2) and ln(AGB)=-2.907+0.932ln(D2H). The diameter-height allometry was ln(H)=0.469+1.082ln(d)-0.106ln(D)2.The relative error of biomass estimation of subtropical forest applied by moist tropical forest biomass model with height as a predictor from Chave was less than models without height as a predictor. The pan equations from Basuki, Brown, Chan, Ketterings, and Kenzo were not valid for the mid-subtropical broad-leaved forest. But the pan equations from Ogawa was the best valid for the biomass carbon estimation. The result showed that using pan allometric equations to estimate the suitability of the biomass carbon pool in mid subtropical evergreen broad leaved forest need to test its applicability and identify the number and DBH rang of tree.

biomass model; allometric equations; evergreen broad leaved forest; biomass carbon pool

S718.55+6

A

1673-923X(2017)11-0115-06

10.14067/j.cnki.1673-923x.2017.11.019

2016-08-01

国家自然科学基金重点项目（31130013）

林开淼，博士研究生；E-mail：303790102@qq.com

林开淼.亚热带常绿阔叶林生物量模型及其分析[J].中南林业科技大学学报，2017, 37(11): 115-120, 126.

[本文编校：吴 毅]