基于皮尔逊相关系数的电网夏季空调负荷预测研究

唐伟斌，李 涛，邹品晶，曾建平，向仲卿，胡斯佳

（1.国网常德供电公司，湖南 常德 415000；2.国网岳阳供电公司，湖南 岳阳 414000；3.湖南大学，长沙 410082）

◆研究与探讨◆

基于皮尔逊相关系数的电网夏季空调负荷预测研究

唐伟斌1，李 涛1，邹品晶2，曾建平1，向仲卿1，胡斯佳3

（1.国网常德供电公司，湖南 常德 415000；2.国网岳阳供电公司，湖南 岳阳 414000；3.湖南大学，长沙 410082）

采用统计分析的方式研究地区电网夏季空调负荷的变化规律，综合考虑空调负荷的影响因素，构建了地区电网夏季空调负荷预测模型。该模型以地区电网负荷变化曲线为基础，实现了对空调负荷曲线的有效分离，随后采用Pearson相关系数考察各类影响因素与日最大空调降温负荷的相关性，通过比较日最大空调降温负荷与各类指标的相关系数，构造出一个能够体现最大空调负荷受本地区气象和社会经济影响较大的“经济气象综合指标”，并利用回归分析提炼出空调降温负荷与综合指标的变化规律，最终实现夏季空调负荷的精准预测。基于某地区电网2006—2015年电力负荷及其相关数据，使用该模型预测2016年该地区电网夏季空调负荷，预测结果证明了模型的有效性。

空调降温负荷；Pearson相关系数；经济气象综合指标；预测模型

近年来，随着人民物质文化生活水平的提高，居民用电和商业用电负荷所占的比例越来越大，其中夏季空调负荷和冬季取暖负荷是较为突出的两类负荷，很多地区空调降温负荷在年最大负荷中的占比已过半。空调降温负荷的准确预测对全省及各地市开展夏季电力市场分析预测、季度及月度电力市场跟踪分析具有很强的实用价值，对科学安排年度电网运行方式，科学决策电网建设，提高电网投资精准性具有现实的指导意义。

空调降温负荷与气温等气象因素有着密切的联系，长期以来，许多气象和电力专家都致力于充分利用气象因素研究电力负荷的发展特征。文献［1］—文献［2］中针对母线负荷数量众多的特点，结合NWP数据对每个负荷进行数据分析与计算。但该方法运算量大，占用系统资源多，其运算速度会受到影响。文献［3］—文献［4］中，如果能够获得未来负荷变化的连续的概率密度函数，分析负荷分布区间的概率，则可了解未来负荷的变化波动范围，然而，概率密度预测的方法需要依赖于更多的理论推导，涉及到复杂的数学计算。文献［5］—文献［6］表明，空调降温负荷不仅与历史负荷数据有关，很大程度上还受气象因素的影响，但是气象因子比较多，且各个因素之间都存在一定信息互嵌，直接使用会造成信息冗余，增加计算复杂度。

本文借鉴以往研究经验，以地区电网为例，结合地区的具体特点，创立新方法，考察地区夏季空调负荷与各类因素的联系，为掌握预测年度空调负荷提供有效的参考。

1 电网夏季空调负荷的提取及其气象影响因素分析

1.1 空调负荷的提取方法

负荷的变化受到多种因素的制约，准确地对负荷进行分离是一项复杂而又困难的工作。特别是空调负荷是指空调设备运行所消耗的电力。由于无法精确统计，因此只能用电网的负荷曲线来模拟测算,也就是空调开启之后的电网负荷与空调未开启时的电网负荷之差。本文采用基准负荷比较法［7—8］。

下文所用电网负荷数据来源于华中地区某地市电网调度SCADA系统整点负荷数据，气象数据来源于气象部门公开的气象资料，社会经济相关数据来源于政府统计部门公开数据。

图1所示为某地区电网2006—2015年负荷特性曲线，由图可以看出，该地区春季和秋季气温比较凉爽，很少开启空调设备，因此可将4月或5月的日负荷曲线与10月或11月的日负荷曲线叠加取平均值，可以消除负荷自然增长的影响，得到夏季电网每日不含空调的基础用电负荷曲线。

图1 某地区电网2006—2015年负荷特性曲线

春季4月或5月平均日负荷曲线的计算方法

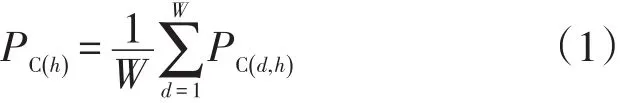
式中：PC(h)为春季4月或5月平均日负荷曲线；PC(d,h)为春季每个工作日的负荷曲线；W为当月工作日的总天数；d为当月1—W个工作日；h为当日1—24 h。

秋季10月或11月平均日负荷曲线的计算方法

式中：PQ(h)为秋季10月或11月平均日负荷曲线；PQ(d,h)为秋季每个工作日的负荷曲线。

以春季和秋季负荷曲线的平均值为基础负荷曲线，再取夏季每天的日负荷曲线与基础负荷曲线的差值，作为当天的空调负荷曲线，由此可计算得到2006—2015年夏季每天的空调负荷曲线。其中，各年夏季最大负荷日的空调负荷曲线如图2所示。可见，空调负荷水平除受气象因素影响外，总体上呈增长趋势，这和社会经济及城镇化的发展趋势是一致的。

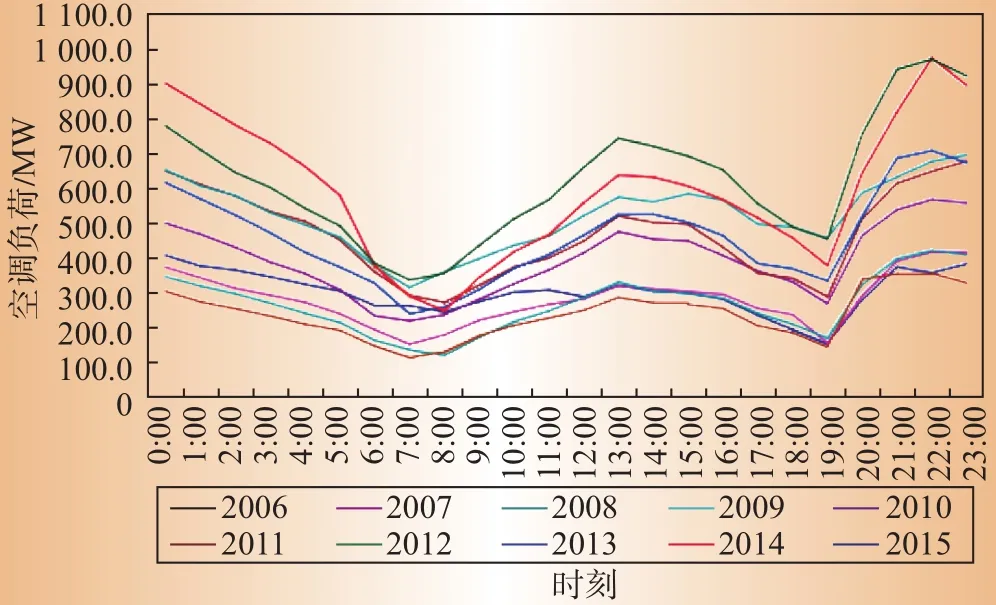
图2 某地区电网2006—2015年最大负荷日空调负荷曲线

1.2 影响电网夏季空调负荷变化的气象因素分析

决定夏季空调负荷水平最重要的气象因素是气温。文献［9］—文献［10］研究指出，湿度、风速、降水量等气象因素与空调负荷的大样本统计相关性很弱，本文基于本地区2006—2015年的实际气象和负荷数据进行了相关性分析，也得到了类似的结论，具体计算结果见表1。

因此，本文仅考虑气温与空调负荷的关系，采用每日气温数据作为预测模型建立的依据。

2 空调负荷与其影响因素的相关性分析

2.1 空调负荷与其气象影响因素的相关性分析

本文采用Pearson相关系数来考察各类因素对日最大空调负荷的影响力，相关系数按公式（3）计算

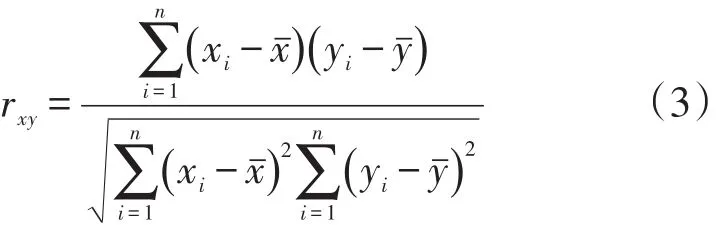
式中：{xi,i=1,2,…,n} 和{yi,i=1,2,…,n}分别为两组长度为n的数列。

两变量之间的相关性可由相关系数初步决定，但须进行显著性检验再最后判断。其显著性检验公式为

2.1.1 日最大空调负荷与各类单一气温指标的相关性分析

分别计算日最高气温、日平均气温、日算术平均气温、日平均湿度、日平均风速、日降水量等指标与日最大空调负荷的相关系数，如表1所示。表1中每年度的日降水量指标与日最大空调负荷的相关性已通过0.05显著性检验，其它气象指标与日最大空调负荷的相关性已通过0.01显著性检验。

表1中第一行的0.708指的是2006年夏季6—9月每天的当日最大空调负荷的数列和当日最高气温数列的相关系数，其他数据以此类推。

表1 日最大空调负荷与各种单一气温指标的相关性

气温对空调负荷存在多日积累效应，连续几天高温与当天突然高温这两种情况下的空调负荷会有明显差别。为有效地描述积累效应对当天空调负荷的影响，对每天空调负荷，可分别考察当天以前的1天、3天、5天、13天以内的平均气温对其影响，影响力的大小用相关系数来描述，计算结果见表2所示。

表2中第一行的0.675指的是2006年夏季6—9月每天的当日最大空调负荷的数列和前一日最高气温数列的相关系数，表2中其他数据的含义以此类推。各年度相关系数均已通过0.01显著性检验，2006—2015年各相关系数已通过0.001显著性检验。以上数据表明，过去几天的气温与日最大空调负荷有着明显的相关性，表2中的4个气温指标能够作为反映积累效应的有效指标。

2.1.3 日最大空调负荷与综合积累气温指标的相关性分析

为了更清楚地考察气温对空调负荷多日积累效应的关系，本文将当天的算术平均气温a、过去1天的平均气温b、过去3天的平均气温c、过去5天的平均气温d、过去13天的平均气温e等5个气温指标进行线性组合，构成综合积累气温指标，根据某地区2006—2015年的实际数据，以该指标数列与日最大空调负荷数列在2006—2015年间总的相关系数最大为目标，计算得出了形成综合积累气温指标p的最优线性组合

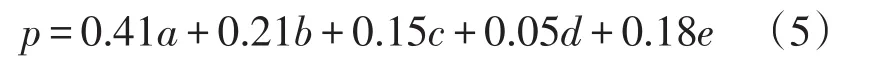
线性组合中的权重系数是通过计算机程序以［0，1］为区间、0.01为步长，遍历该范围内所有系数取值，最后取与空调负荷相关性最佳者而得到，式（3）得到权重系数的综合积累气温数列与日最大空调负荷数列之间的相关系数最大。

综合积累气温指标与日最大空调负荷之间的相关系数计算结果见表2。

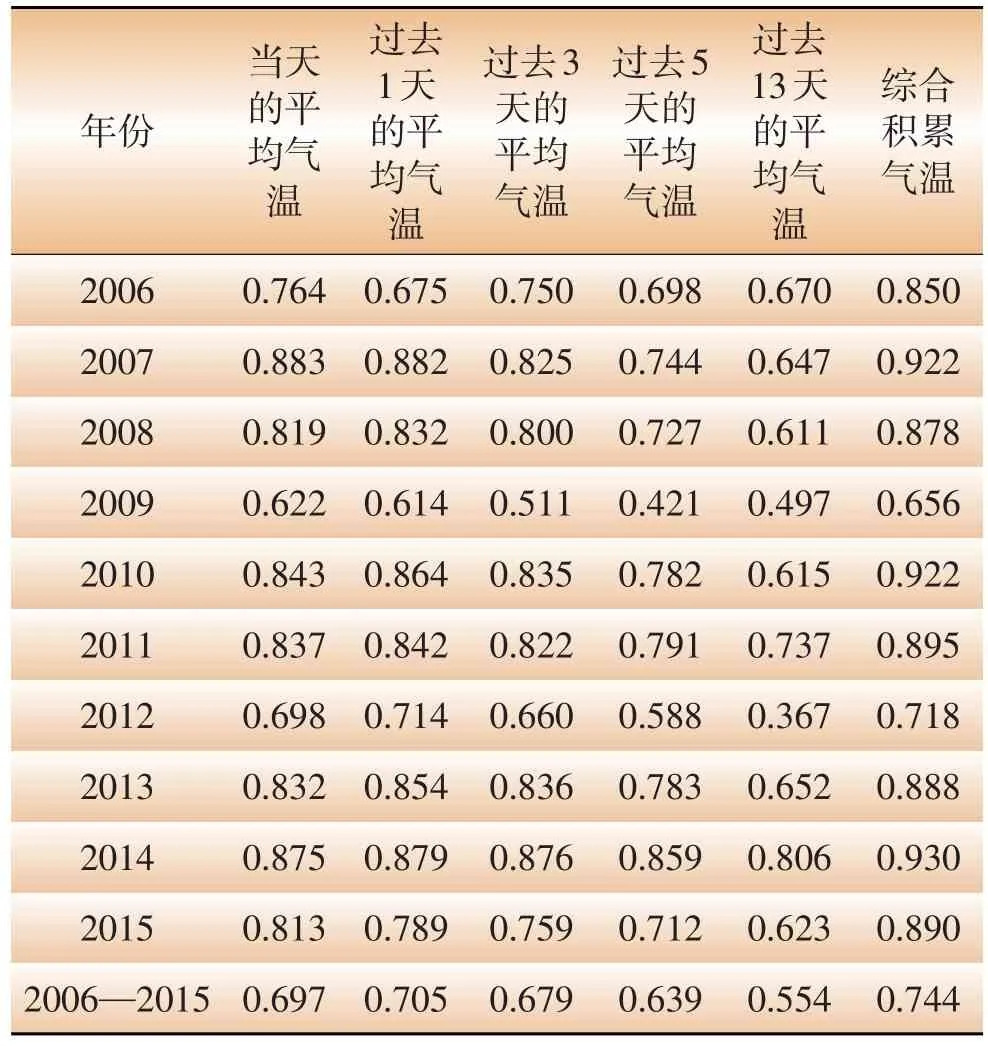
表2 日最大空调负荷与综合积累气温指标的相关性

表2中第一行的0.850指的是2006年夏季6—9月每日综合积累气温数列和当日最大空调负荷数列的相关系数，表中其他数据以此类推。表中各年度相关系数均已通过0.01显著性检验，2006—2015年各相关系数已通过0.001显著性检验。可以看出，新指标“综合积累气温”与日最大空调负荷之间的相关性更强。

图3是“日平均气温-日最大空调负荷”散点图，图4是“日综合积累气温-日最大空调负荷”散点图，横坐标是温度，纵坐标是负荷。图3中散在的数据点在图4中很好地会聚到了一起，这说明“综合积累气温”确实地反映了“温度-负荷”特性的内在规律。

根据区内工勘孔及有关调查资料，池州市中心城区地下水位埋深一般0.4～5.0 m，局部地下水位埋深为9.7 m(位置较高处)，地下水位埋深整体较浅，年变幅小于1 m。

2.2 空调负荷与其非气象影响因素的相关性分析

空调负荷水平的变化除了受气象因素的影响之外，还会随着地区经济发展而变化，如GDP、居民收入、消费能力等因素。比如：分析某地区2006—2015年数据可知，地区空调负荷水平与地区生产总值GDP、居民收入之间呈正相关，如图5和图6所示。

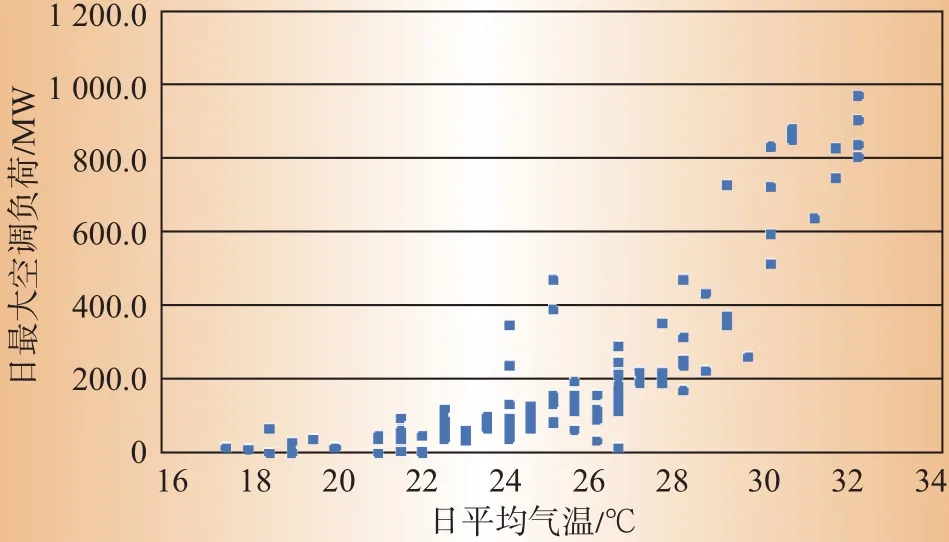
图3 某地区电网2015年夏季“日平均气温”与“日最大空调负荷”散点图

图4 某地区电网2015年夏季“日综合积累气温”与“日最大空调负荷”散点图

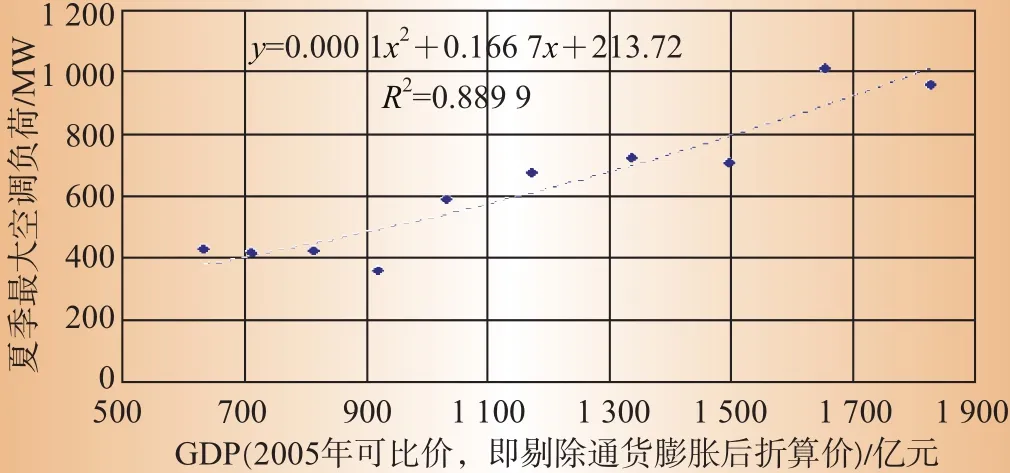
图5 2006—2015年夏季最大空调负荷与GDP二次多项式回归

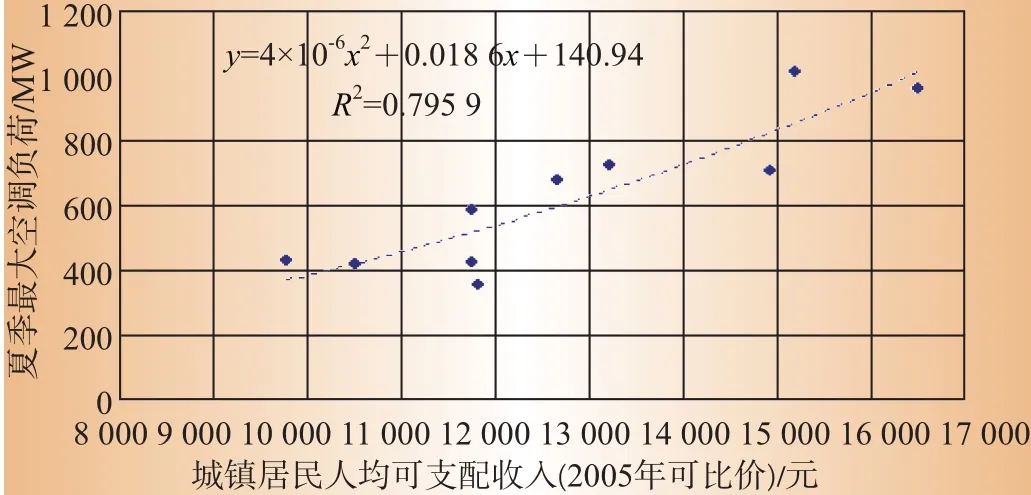
图6 2006—2015年夏季最大空调负荷与城镇居民人均可支配收入二次多项式回归

数据还表明，地区每年夏季的最大空调负荷除受气象因素影响外，也随地区生产总值GDP等社会经济指标的变化而变化，由图6可以看出，空调负荷与经济指标的共变趋势是非线性的，各年度最大空调负荷数据偏离回归曲线的趋势与表1中各年度实际的总体气温水平基本相符。

更细致地，考察各年度在相同气象条件下的最大空调负荷的变化情况，如表3所示，将综合积累气温分成若干小区间，表3中列出了2006—2015年各年度在同一气温区间中的最大空调负荷。

表3中第一行的164.4指的是2006年夏季6—9月共122天中，所有当日综合积累气温在26.75℃至27.25℃之间的工作日或非工作日中最大的空调负荷，其他数据以此类推。

从表3数据中可以看出，在综合积累气温水平较高的区间（区间中心≥30），空调负荷的增长对GDP增长的敏感性较强，在综合积累气温水平较低的区间（区间中心＜30），敏感性较弱。

比较图5、图6和表1，各年度最大空调负荷水平受当年总体气温水平影响，当年总体气温水平高则空调负荷水平高，反之则较低；又如表3所示，各个气温水平下的空调负荷水平总体上随着经济因素的增长而增长。因此，经济因素和气温因素结合，可以更完整地描述各年夏季最大空调负荷的变化规律。

2.3 空调负荷与经济气象综合指标的相关性分析

以表3中的数据为基础，研究构造适用于反映夏季本地区最大空调负荷随气象和社会经济条件变化规律的“经济气象综合指标”，并以使两者的相关系数达到最大为目标，构建“经济气象综合指标”的最佳计算公式。

通过对经济因素与综合积累气温组合方式的大量尝试，构造出了式（6）描述的“经济气象综合指标”。通过计算机程序对式（6）中各个参数分别设定取值范围和步长，遍历取得范围内所有可能的参数值，分别计算各种参数值下得到的式（6）与空调负荷的相关系数，再取相关系数最大者。

式中：z为经济气象综合指标；p为综合积累气温指标；g、h分别为影响空调负荷的某个社会经济指标，如GDP、居民人均可支配收入等；w1为纯气象项权重系数，w2、w3为社会经济项的权重系数，它们满足w1+w2+w3+…=1；g0、h0、…为社会经济因素的参照值；a、p1、p2、p3、c1、c2、c3、…参数与权重系数一起，需要通过计算机程序按一定取值范围和步长、遍历所有可能值，最后取与空调负荷相关性最佳者而得到，根据计算，能使相关系数达到最佳的参数在如下范围：a、c1、c2、c3、w1、w2、w3、…取值［0，1］区间，p1、p2、p3、…取值［28，32］区间。

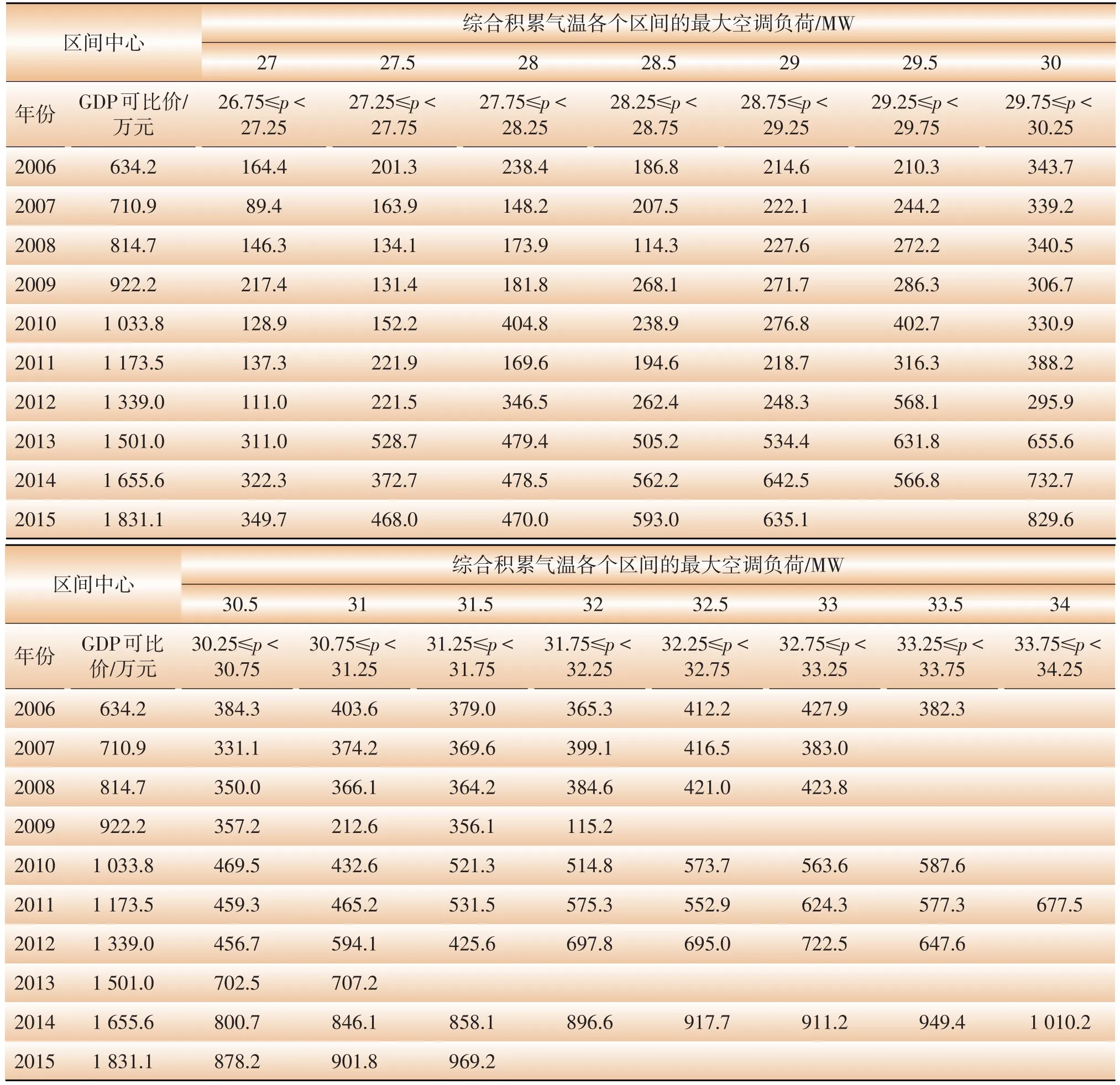
表3 综合积累气温各个区间的最大空调负荷

以该地区的实际数据为例，通过计算各个参数，得到该地区电网关于夏季最大空调负荷的“经济气象综合指标”

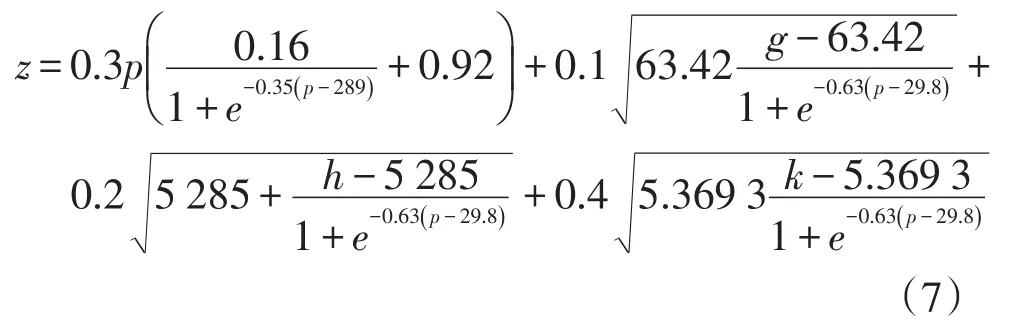
式中：g为GDP可比价，亿元；h为居民人均可支配收入，元；k为常住人口，百万人。

将2006—2015年“经济气象综合指标z”与夏季各温度区间中的最大空调负荷之间的数据绘制成散点图如图7所示。

图7 2006—2015年“经济气象综合指标z”与夏季各温度区间中的最大空调负荷散点图

显然，构造的“经济气象综合指标z”与最大空调负荷有显著的相关性，计算得到的相关系数为0.951，且通过0.001显著性检验。

3 空调负荷预测模型的建立

3.1 模型建立

一般地，以上面构造的“经济气象综合指标z”为基础，就可建立最大空调负荷的年度预测模型

以文中所给地区的情况为例，将图7中的回归模型作为该地区最大空调负荷年度预测模型

3.2 模型检验

（1）拟合度检验

本模型的拟合优度检验结果见表4。其中R2是相关系数的平方，用于判定线性回归的拟合程度。表4表明本模型的拟合系数为0.924，显示本模型具有较高的拟合度。

表4 拟合度检验

（2）方差检验

本模型的方差检验结果见表5，表5中数据显示：F=2 720，Sig.F=2.8×10-127，表明本模型回归因子的影响极为显著。

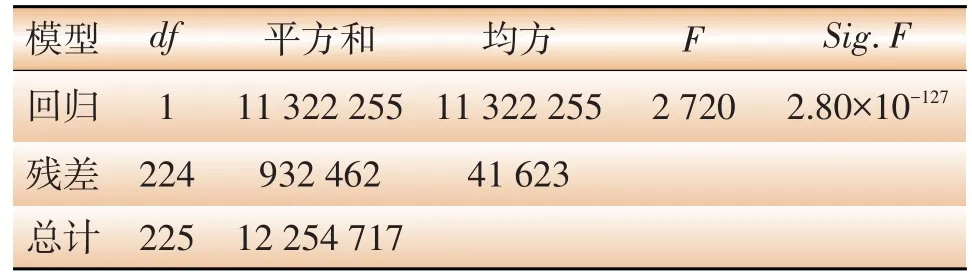
表5 方差检验

（3）回代检验

利用该预测模型即式（9），可算出2010年至2015年空调负荷回代值和预测误差，见表6。

表6 回代检验

从表6可看出，利用该模型算出的2010—2015年空调负荷预测值的误差率均在4%以内。

4 2016年夏季空调负荷预测实例

本节以2006—2015年作为历史数据年，以2016年作为预测年。本节仅对空调负荷的预测进行阐述，空调负荷预测结果与基础负荷预测结果进行合并即可得到全网总负荷的预测结果。某地区2013—2015年及2016年第一季度GDP情况如表7所示。

表7 某地区2013—2016年GDP情况

如果在2016年第二季度对夏季最大负荷水平进行预测，根据2016年初该地区政府工作报告2016年该地区GDP增速为9.0%，约为1 995.9亿元（2005年可比价），居民人均收入增速为12%，达到13 211.6元，预期年末常住人口587万人，代入式（7）、式（9），计算得到了预测年在各种不同气温水平下的负荷预测结果，见表8。

表8 2016年夏季最大空调负荷预测

若按实测气温计算得到的综合积累气温30.6℃来计算，得到的夏季最大空调负荷预测值为878.4 MW，与按2.1节所述方式，实际测算的当年夏季最大空调负荷900.6 MW相比，误差率为2.48%。

将此空调负荷预测结果与基础负荷预测结果进行合并即可得到全网总负荷的预测结果。

5 结束语

本文基于2006—2015年夏季某地区电网整点负荷数据和每日气象实测数据，考察负荷与各类因素的关系，提出了“综合积累气温指标 p”和“经济气象综合指标z”，并具体给出了描述制约关系的计算公式，建立了该地区夏季最大空调负荷的预测模型，并通过对2016年该地区电网夏季空调负荷预测的实践，证明了其实用性和可行性。需要指出的是，本文在建模过程中对一些次要因素（如夏季排灌负荷等）进行了一定的忽略和简化。在极端天气导致洪涝等特殊情况时，排灌负荷占比较大时，单纯应用本方法预测将有所失真，今后需进一步研究优化。

［1］ 李博，门德月，严亚勤，等.基于数值天气预报的母线负荷预测［J］.电力系统自动化，2015（1）：137-140.

［2］ 韩力，韩学山，贠志皓，等.多节点超短期负荷预测方法［J］.电力系统自动化，2007，31（21）：30-34.

［3］ 何耀耀，闻才喜，许启发，等.考虑温度因素的中期电力负荷概率密度预测方法［J］.电网技术，2015，39（1）：176-181.

［4］ 肖白，周潮，穆钢.空间电力负荷预测方法综述与展望［J］.中国电机工程学报2013，33（25）：78-92.

［5］ 张淑清，任爽，师荣艳，等.基于多变量气象因子的LMBP电力日负荷预测［J］.仪器仪表学报，2015，36（7）：47-52.

［6］ 黎灿兵，杨朋，刘玮.短期负荷预测中考虑夏季气温累积效应的方法［J］.电力系统自动化，2009，33（9）：96-99.

［7］ 温权，李敬如，赵静.空调负荷计算方法及应用［J］.电力需求侧管理，2005，7（4）：16-18.

［8］ 楚成博，刘继东，张利，等.山东电网夏季降温负荷特性及影响因素分析［J］.电力需求侧管理，2013，15（1）：20-24.

［9］ 李欣然，姜学皎，钱军，等.基于用户日负荷曲线的用电行业分类与综合方法［J］.电力系统自动化2010，34（10）：56-61.

［10］ 李晓林.辽宁电网负荷与气象信息相关性研究［D］.保定：华北电力大学，2014.

Air-condition load forecasting in summer of power grid using pearson correlation coefficient

TANGWei-bin1,LITao1,ZOUPin-jing2,ZENGJian-ping1,XIANGZhong-qing1,HUSi-jia3
（1.State Grid Changde Supply Company,Changde 415000,China;2.State Grid Yueyang Supply Company,Yueyang 414000,China;3.Hunan University,Changsha 410082,China）

In this paper,the variation rule of the air-conditioning load in summer regional power grid can be obtained using statistical analysis.By overall considering the influencing factors of air-conditioning load,the forecasting model of summer air-conditioning load in regional power grid was built.The model was based on the load curves of the regional power grid,and realized the effective separation of the air-conditioning load curve.Then the Pearson correlation coefficient was used to investigate the correlation between various factors and daily maximum air-conditioning cooling load.Through comparing the correlation coefficient between the daily maximum air-conditioning cooling load and all kinds of indexes,an economic-meteorological comprehensive index,reflecting the fact that the daily maximum air-conditioning load is greatly affected by the meteorological and socio-economic in a region,was constructed.And the regression analysis was used to extract the change rule of the air conditioning cooling load and the comprehensive index.Finally,the accurate prediction of summer air-conditioning load is realized.A regional data of power load and its related factors from 2006 to 2015 was used as training sample to forecast the summer airconditioning load in 2016 of the region.The forecasting results proved the validity of the proposed model.

air-conditioning cooling load;Pearson correlation coefficient;the economic-meteorological comprehensive index;forecasting model

TM714

B

1009-1831（2017）06-0007-07

10.3969/j.issn.1009-1831.2017.06.003

2017-07-13；

2017-08-23

唐伟斌（1976），男，湖南常德人，工学硕士，高级工程师，研究方向为电网调度与经济运行。