针对杂波抑制的超宽带MIMO雷达自适应波形设计

季晨荷，宋耀良

(南京理工大学 电子工程与光电技术学院， 江苏 南京 210094)

针对杂波抑制的超宽带MIMO雷达自适应波形设计

季晨荷，宋耀良

(南京理工大学 电子工程与光电技术学院， 江苏 南京 210094)

为有效提高复杂环境下的杂波抑制能力，本文提出了一种基于仅发射分集分布式超宽带MIMO雷达体制下的波形自适应优化方法。该方法通过波束形成技术将兴趣目标与杂波目标分离，并通过计算不同目标间互信息值的大小，对下一时刻的发射波形进行优选；最后根据测得目标频域参数信息对发射信号能量进行优化分配。理论分析和仿真结果表明：在多杂波目标干扰的复杂环境下，本文方法可以获取更多的检测目标信息量，进而提高目标的检测性能。

超宽带； MIMO雷达； 波束成形； 波形设计； 信息量； 自适应； 杂波

近年来，超宽带MIMO雷达受到了业界越来越多的关注[1-4]。超宽带技术与MIMO雷达相结合不仅提高了雷达系统的分辨能力，同时也增加了信号的信息承载量，很大程度上提高了MIMO雷达的系统性能。因此针对超宽带MIMO雷达的研究具有十分重要的现实意义。

目前，在复杂的雷达环境下，超宽带雷达回波中除包含目标信息外，还存在大量杂波和干扰。由于各种障碍物的衰减作用，目标的回波信号通常较为微弱，容易被淹没在背景杂波和噪声中。 如果不进行有效的杂波抑制，则会对目标检测带来极大的困扰。因此，如何有效抑制杂波干扰是超宽带体制下MIMO雷达所需研究的重要课题之一。对于MIMO雷达而言，由于其天线结构的特点，使得发射波形更加灵活，因此本文考虑通过优化发射波形的方法达到杂波抑制的效果。文献[5]在噪声环境中分别以Chernoff上限准则、互信息准则和信杂比准则推导出最优检测MIMO波形设计，文献[6]通过对杂波进行统计建模并对模型参数在线估计，设计了能够最小化杂波能量的发射波形，改善了复杂场景中目标的检测性能。文献[7]是在杂波环境中，利用序贯假设检验方法进行检测波形设计。文献[8]分别给出了在确定性信道和随机信道条件下对MIMO雷达波形设计，并用投影法解决了相关杂波处理问题，仿真充分证明了此方法的可行性。

上述研究在波形优化设计方面取得了优异的成果，但他们的研究都是基于窄带MIMO雷达基础上的。随着发射信号带宽的增加，目标与杂波特征都发生了改变，原有的设计方法不再能适用于当前的系统。因此，本文针对宽带体制提出了一种自适应波形设计方法，对杂波进行了有效的抑制。

1 超宽带MIMO雷达系统模型

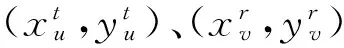
rvu(fn)=

(1)

式中：τk,v和τu,k分别代表散射中心与发射和接收端之间的时延。所以超宽带MIMO雷达接收信号表示为

r(fn)=[r1(fn)…ru(fn)…rU(fn)]V×U

(2)

其中

(3)

此外，考虑到超宽带体制下信号分辨能力的提升，在复杂的雷达检测环境中，除了兴趣目标外，也检测到许多杂波目标的存在。于是本文将兴趣目标与杂波目标的信道矩阵分别表示为HT、HI。由此可以将系统模型的表示为

r=rT+rI+N=HTS+HIS+N

(4)

图1 天线收发端与目标坐标图Fig.1 The coordinate graph of antenna and target

2 系统架构选择

在目标与杂波干扰并存的复杂雷达环境中，若不能有效抑制杂波干扰，雷达的检测性能势必要受到极大的影响。MIMO雷达天线布阵方式分为很多种，针对杂波抑制的设计需求，本文考虑采用仅发射分集的分布式阵列架构，通过这一设置，雷达系统既能满足发射信号空间分集，以此提高对起伏目标的检测能力，又可以在利用接收端波束形成技术有效地抑制干扰，从而提高输出信干噪比(SINR)，改善对目标的检测能力。

Fishler基于Neyman-Pearson准则分析了不同系统架构下的MIMO雷达的检测性能[9]。本文将这种方法扩展到上节所提出的雷达系统模型中，并对提出模型的雷达检测性能进行了分析与比较(为了简化表达，下文中收发全分集分布式架构MIMO雷达简称为D-MIMO；仅发射分集分布式构架MIMO雷达简称为S-MIMO)。

全分集MIMO雷达优化检测器表达式为

TD-MIMO=‖x‖2

(5)

式中：x代表UV×N维的匹配滤波器输出矢量。TD-MIMO的分布形式为

(6)

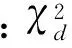
同样，对于S-MIMO而言，其优化检测器表达式为

TS-MIMO=‖x′‖2

(7)

式中：x′代表U×N维的匹配滤波器输出矢量。TS-MIMO的分布形式为

(8)

根据文献[10]可以得到基于雷达检测器信干噪比(SINR)的表达式：

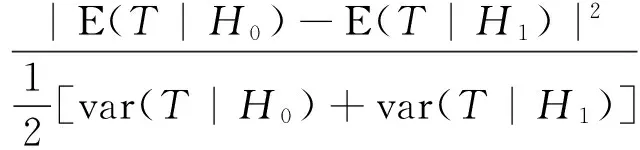
(9)

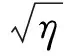
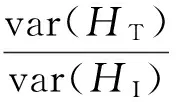
情况1：当ρ=1，即信号功率与噪声功率相同时，优化检测器SINR可以表示为

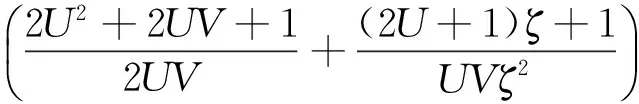
(10)

(11)

如图2(a)所示，S-MIMO雷达的信干噪比值大于D-MIMO雷达，所以在信噪比等于1的情况下，S-MIMO的检测性能更为优异。

图2 不同信噪比下的优化检测器SINR输出Fig.2 The optimal detector SINR output for different SNR

情况2：当ρ≫1, 即信号功率远远大于噪声功率时，优化检测器SINR可以表示为

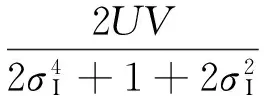
(12)

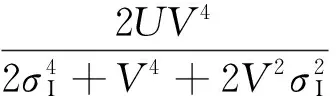
(13)

由图2(b)可以看出兴趣目标信道响应方差小于杂波目标信道方差时，S-MIMO雷达的信干噪比值大于D-MIMO雷达。

情况3：当ρ≪1, 即信号功率远远小于噪声功率时，优化检测器SINR可以表示为

(14)

(15)

由式(14)、(15)可以看出在这种情况下，S-MIMO雷达的检测性能要优于D-MIMO雷达。

综合以上可知：在多数情况下，针对存在杂波目标的复杂雷达环境，S-MIMO雷达对目标的检测能力要优于D-MIMO雷达。所以本文的研究将基于仅发射分集的分布式MIMO雷达构架展开。

3 基于信息理论的波形自适应设计

为进一步提升对兴趣目标的检测能力，加强对杂波目标的抑制效果，本文拟从波形设计的角度出发，提出了一种基于信息理论的自适应波形优化设计方法。该方法主要分为波形优选、波形功率优化分配两个步骤。

3.1波形优选

基于目标先验信息，本文通过波束形成技术分别对来自兴趣目标与杂波目标的回波进行加权合成，可以得到

YT=wTr=wT(HT+HI)S+N

(16)

YI=wIr=wI(HT+HI)S+N

(17)

式中：YT和YI分别表示经过波束形成后的对应目标的接收信号，wT和wI则分别表示对应的波束形成矢量。由于在每个接收端的噪声信号均是统计独立的，所以本文并没有考虑波形形成对噪声的影响。为了简化表示，令QT=wT(HT+HI)，QI=wI(HT+HI)。接着可以用YT/I,t和YT/I,t-1表示两个连续时刻的接收信号矢量。由式(16)、(17)可以得到

(18)

(19)

(20)

(21)

通过式(18)～(21)可以计算出RQT、RQI以及RN。由此可以估算出波形集合中的任意波形St+1∈作为发射波形后，接收端所收到的信号矢量YT/I,t+1。

根据信息论，任意两个矢量满足统计独立，其互信息值达到最小。如果两个矢量分别表示来自兴趣目标与杂波目标的回波信号，则当其互信息值最小时，雷达所获取的来自兴趣目标与杂波目标的信息量就越大。换句话说，波形优选的目的在于从信号集中选取St+1使得来自兴趣目标与杂波目标的互信息值达到最小。通过互信息值的计算，可以得到

I(YT,YI)=

H(YT|S)+H(YI|S)-H(YT,YI|S)

(22)

根据推导，设计的最小化互信息准则可以表示为

(23)

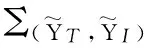
化处理;P0为总发射功率。

3.2波形功率优化分配

根据3.1节的优化准则，可以选出波形集合内针对当前环境最适合的发射波形，以获得最多的兴趣目标与杂波目标信息。接下来，本文针对超宽带信号频域丰富的特点，考虑采用频域能量优化分配的方式，进一步提高对杂波的抑制效果。根据信息理论，可以得到关于兴趣目标回波信号和接收波束之间在频率fn处的交互信息：

In(HT(fn);r(fn)|S(fn))=

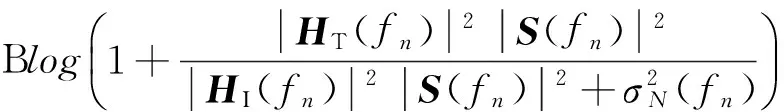
(24)

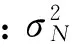
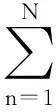
(25)

由此可以得到兴趣目标与接收波束间的总互信息值。当然，不同的目标具有不同的代价函数，设计的波形不可能满足所有目标的需求。为了解决这一问题，本文考虑多组波形联合设计方法，组数取决于信道内存在的兴趣目标数。故多组波形设计问题可以表述为

(26)

该问题的极值可以通过拉格朗日极值法进行估算。令

L(|S(f)|2,λ)=

(27)

本文设定实际发射能量满足：

|S(f)|2≤P0/U

(28)

由式(27)、(28)可以看出信干噪比是一个随P0增大而单调递增的函数。因此不等式(28)可以等效为等式形式，进而得出当SINR取最大值时有：

∂SINRmax/∂(P0/U)>0

(29)

由于λ=∂SINRmax/∂(P0/U)，因此可以变相的证明拉格朗日算子为正数。所以式(30)求最大极值的问题可以转换为

(31)

根据极值求解法可得

|S(f)|2=

(32)

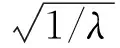
根据Bell的注水理论设计原理当杂波目标回波响应幅度较大而检测目标回波响应幅度较小时，要降低该频率内的信号功率；而当杂波目标回波响应幅度较小而检测目标回波响应幅度较大时，则需要加强该频率内的信号功率。当然，对应不同的兴趣目标，优化功率分布的方法也不一样。可以根据兴趣目标的数量，生成对应的自适应优化发射波形。

3.3波形设计自适应机制

依上所述，本文的自适应波形设计是一种以最优化检测为准则的波形优选方法，其过程如下：

1)生成具有良好相关特性的发射波形，将这些波形设定为一个集合;

2)根据对接收信号连续时刻的测量，估算出RQT、RQI和RN；

4)根据得到的t时刻各个目标的频域回波响应的大小差异，调整发射信号St+1的功率谱密度，达到抑制杂波目标，提高兴趣目标检测概率的目的；

5)将优化后的信号S′t+1作为t+1时刻的发射信号，随后更新接收信号与目标与环境参数；

6)重复步骤2)～5)。

4 信号功率优化分配仿真

通过仿真实验验证上述自适应波形优化设计方法的可行性与先进性。首先，建立了一个8发8收的MIMO雷达模型，8个发射天线采用分布式布阵，而8个接收天线则采用集中式均匀线性布阵(接收阵阵元间距为λ/2)。发射信号带宽为500 MHz，采样频率为2.4 GHz。为分析方便，假设检测环境中仅存在两个目标，兴趣目标与杂波目标，分别位于接收阵元35°和45°方位。可通过波束形成技术在接收端将两个目标的回波信号分离开来。

波形设计阶段，首先采用最小化互信息准则对发射波形进行优选，如图3所示，信息量随着迭代次数的增多而降低，同时不同的信噪比下信息量的大小也不尽相同。信噪比越大信息量越小，降低速率也越快。这是由于随着信噪比的增加，RQT与RQI的估计精度也在逐渐升高，导致了互信息量的降低。然后根据目标频域响应幅度差异来优化信号能量谱密度。设定目标起伏满足高斯模型且长度分别为30 m和20 m。假设兴趣目标较大，而杂波目标较小，如图4(a)所示，较小的目标时域响应中间高两边低，而较大的目标时域响应中间低两边高。而目标频域响应则完全相反，如图4(b)所示，较大的目标表现出更窄的频域响应，即在低频段大目标的幅值要大于小目标的幅值，高频段则相反。从图5可以看出，发射信号能量并不是集中在杂波功率最小的地方，而是存在于兴趣目标与杂波目标功率差最大的地方。

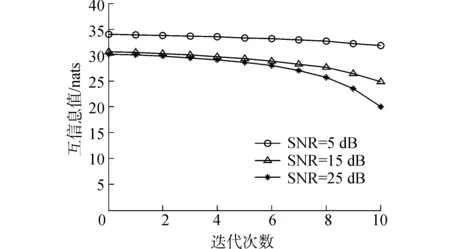
图3 不同信噪比下互信息最小化进程Fig.3 MI minimization process for different SNRs

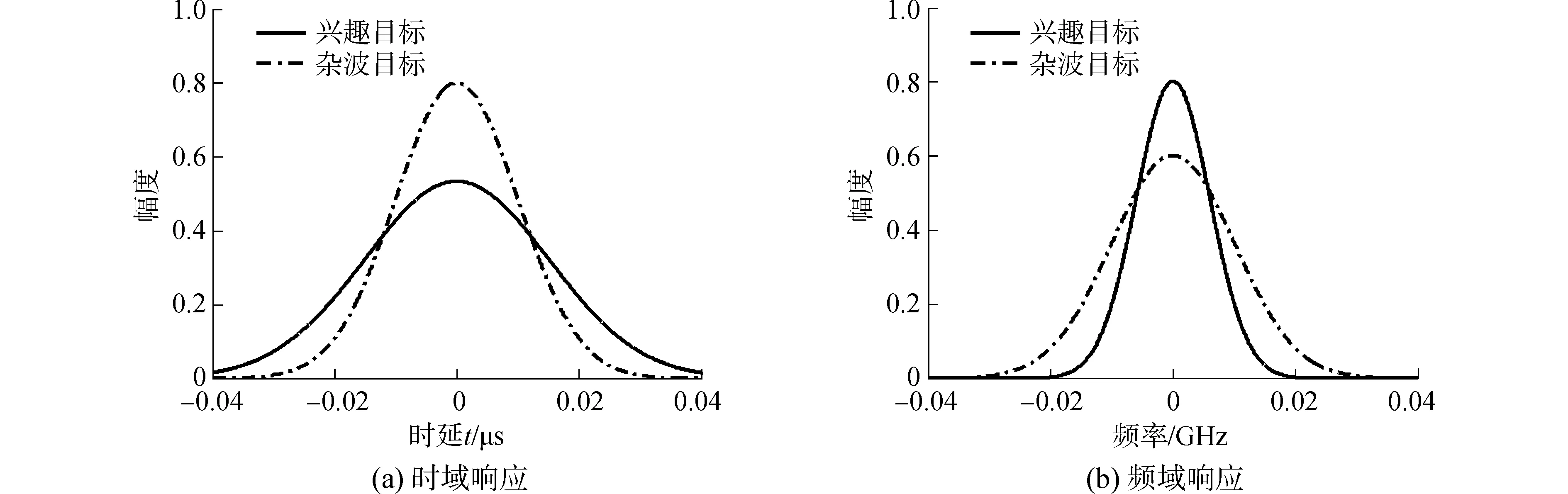
图4 不同目标时域、频域响应Fig.4 Targets time domain response and frequency domain response

图5 发射信号优化能量谱密度以及兴趣目标与杂波杂波目标功率谱密度Fig.5 Optimal transmit ESD and interest target plus clutter target PSD

本节讨论分析所提优化设计方法的自适应特性。假设虚警概率为1×10-4。从图6可以看出随着自适应迭代次数的增多，对兴趣目标的检测概率在不断提升。同时也可以看出随着迭代次数的增加，检测概率的提升幅度也在逐步的减小，且对应值也会趋向于一个极限。最后比较了本文所提出的自适应波形优化方法采用前后的检测概率比较图。如图7所示，采用该方法的检测概率要明显高于未采用该方法的检测概率。

图6 检测概率迭代曲线图Fig.6 Probability of target detection for various iterations

图7 检测概率比较图Fig.7 Comparison of detection probability

5 结论

1) 比较了MIMO雷达不同天线架构下的杂波抑制性能。得出在杂波环境下，仅发射分集的分布式天线架构具备更优的雷达检测能力。

2) 通过比较兴趣目标与杂波的互信息值大小，选取最优发射波形，以获得最大的目标与杂波信息。

3) 针对超宽带信号频域丰富的特点，通过频域功率分配的方式可以提高兴趣目标的检测能力，有效抑制杂波干扰。

[1] SALMI J, MOLISCH A F. Propagation parameter estimation, modeling and measurements for ultra-wideband MIMO radar[J]. IEEE transactions on antennas and propagation, 2011, 59(11): 4257-4267.

[2] CHEN W J, NARAYANAN R M. CGLRT plus TDL beamforming for ultra-wideband MIMO noise radar[J]. IEEE transactions on aerospace and electronic systems, 2012, 48(3): 1858-1869.

[3] CHEN W J, NARAYANAN R M. Antenna placement for minimizing target localization error in UWB MIMO noise radar[J]. IEEE antennas and wireless propagation letters, 2011, 10: 135-138.

[4] NIJSURE Y, KADDOUM G, LEUNG H. Cognitive chaotic UWB-MIMO radar based on nonparametric bayesian technique[J]. IEEE transactions on aerospace and electronic systems, 2015, 51(3): 2360-2378.

[5] LI J, STOICA P. MIMO radar signal processing [M]. Hoboken, New Jersey: John Wiley & Sons, Inc， 2009．

[6] LI Y, MORAN W, SIRA S P, et al. Adaptive waveform design in rapidly-varying radar scenes[C]// Proc 4thinternational waveform diversity and design conference. Kissimmee, USA, 2009: 263-267.

[7] MOTI T, JOSEPH T. Waveform design for sequential detection with subspace interference[C]// IEEE sensor array and multichannel signal processing workshop, 2012: 401-404．

[8] CHEN C Y, VAIDYANATHAN P P. MIMO radar waveform optimization with prior information of the extended target and clutter[J]. IEEE transactions on signal processing, 2009, 57(9): 3533-3544．

[9] FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars-models and detection performance[J]. IEEE transactions on signal processing, 2006, 54(3): 823-838.

[10] SCHARF L L. Statistical signal processing: detection, estimation, and time series analysis[M]. New York: Addison-Wesley Publishing Company, 1991.

[11] LESHEM A, NAPARSTEK O, NEHORAI, et al. Information theoretic adaptive radar waveform design for multiple extended targets[J]. IEEE journal of selected topics in signal processing, 2007, 1(1): 42-55.

[12] KAY S. Optimal signal design for detection of Gaussian point targets in stationary Gaussian clutter reverberation[J]. IEEE journal of selected topics in signal processing, 2007, 1(1): 31-41.

[13] BELL M R. Information theory and radar waveform design[J]. IEEE transactions on information theory, 1993, 39: 1578-1597.

[14] YANG Y, BLUM R S, HE Z S, et al. MIMO radar waveform design via alternating projection[J]. IEEE transactions on signal processing, 2010, 58(3): 1440-1445.

[15] TANG B, TANG J, PENG Y. MIMO radar waveform design in colored noise based on information theory[J]. IEEE transactions on signal processing, 2010, 58(9): 4684-4697.

本文引用格式：

季晨荷，宋耀良. 针对杂波抑制的超宽带MIMO雷达自适应波形设计[J]. 哈尔滨工程大学学报， 2017， 38(11): 1800-1805.

JI Chenhe, SONG Yaoliang. UWB MIMO radar adaptive waveform design for clutter suppression[J]. Journal of Harbin Engineering University， 2017， 38(11): 1800-1805.

UWBMIMOradaradaptivewaveformdesignforcluttersuppression

JI Chenhe, SONG Yaoliang

(School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

To improve the radar clutter rejection ability in a complex environment, this study presents an adaptive optimal waveform design method based on transmit diversity distributed ultra-wideband multi-input multi-output radar. First, the method separates the

signal from target and clutter using beam-forming technology at the receiver. Second, the waveform that is to be transmitted is selected by calculating the mutual information value between different targets. Finally, optimized energy allocation is obtained by measuring the target frequency domain parameters. Theoretical analysis and numerical results show that this method improves target detection performance by acquiring considerable amount of information about the detected target.

ultra-wideband; multiple-input multiple-output radar; beam-forming; waveform design; information; adaptive; clutter

10.11990/jheu.201606038

http://www.cnki.net/kcms/detail/23.1390.u.20170427.1511.092.html

TN958.5

A

1006-7043(2017)11-1800-06

2016-06-14.

网络出版日期：2017-04-27.

国家自然科学基金项目(61071145，61271331).

季晨荷(1984-), 男,博士；

宋耀良(1960-), 男, 教授,博士生导师.

季晨荷，E-mail：princekevin1984@163.com.