船厂钢板堆场混合存储分配及出入库调度研究

侯俊，张志英

(同济大学 机械与能源工程学院，上海 200092)

船厂钢板堆场混合存储分配及出入库调度研究

侯俊，张志英

(同济大学 机械与能源工程学院，上海 200092)

为符合造船厂提出的“分段集批，段齐交货”原则，本文在验证混合存储可行性的同时，优化出入库倒垛作业方案，减少研究周期内出库倒垛次数、降低作业时间和操作成本，从而提高堆场利用率。针对建立的整数规划模型，提出了基于模拟退火接收准则的双层遗传算法(SA-HGA)，在垛位存储分布均匀的基础上制定堆场划分方案，然后根据堆场当前存储状态为将要进入堆场中的两类分段属性的钢板预分配垛位，为需求计划制定作业方案包括倒垛和出库作业组合计划。利用该算法对出入库作业及倒垛方案进行优化，最后将该算法与传统遗传算法作对比，实验证明算法具有有效性和收敛性，并在不同作业规模下，降低了成本预算(4.9%～21.3%)及操作时间(7.6%～10.1%)。

造船厂； 钢板堆场； 分段； 堆场作业计划； 双层遗传算法； 模拟退火

船舶生产过程为分批分段建造，物料需求具有严格的顺序性，船体不同段位需求的钢板规格、数量及期限也严格列出。分段，即钢板生产部门根据船厂生产计划将钢板依次运输至堆场存储，并为其中指定段位所用钢板设分段属性标识。由于生产顺序和周期与需求之间的差异性，存储垛位先入后出的规则，多批次不同类型钢板相互积压，形成倒垛操作。另一方面，船体不同段位所需钢板规格种类繁多，造船厂对船板供应商提出 “分段集批，段齐交货”的原则。钢板堆场出入库作业成本是存储和操作成本中占比不可忽视的一部分。目前造船业相关研究主要集中于实现自动化和信息化管理，相近领域也有炼钢厂热轧板堆场作业优化的研究。造船领域中，施敏等提出了垛位自动预约技术以实现船板自动入库空间分配[1]。徐萍等为应对管理现状与供货要求，提出了构建堆场管理信息系统的开发方案[2]。刘建峰等为船板入库滚动作业建立了基于优化算法的仿真模型，研究钢板入库分配策略[3]。在热轧炼钢行业，蒋如宏等针对板坯出库作业建立静态和动态数字化仿真模型，提高堆场管理信息化水平[4]。唐立新等针对倒垛问题提出了整数规划模型，采用动态启发式算法优化解决方案[5]，李耀华等为热轧板坯出库建立倒垛决策模型，运用粒子群算法以最小化倒垛量[6]。以上研究从不同角度探讨了堆场管理改进方案。但无委托热轧板堆场相关研究主要对出入库或倒垛作业进行优化，不考虑指定分段的特殊属性。造船厂钢板堆场为带分段属性板单独分配存储区域，忽略了指定分段属性钢板独立存储方式的潜在问题。如因缺少部分段位延迟交货、占用堆场空间、堆积变形、垛位过高和存储周期过长等。

针对钢板堆场部分钢板带有指定分段的属性，存储限制条件苛刻，需求必须及时响应的问题特殊性。在上述研究的基础上，本文将研究指定分段和无指定分段两种钢板混合存储方式，由于混合存储方式可能带来分段属性不同的钢板相互积压增加倒垛量的问题，因此从出入库作业成本、时间和倒垛量三个维度，建立基于入库决策的出库整数规划分配决策模型。并提出了高度适应问题特殊性的基于模拟退火概率接受准则的双层遗传算法，通过实验分析对比验证算法的有效性。

1 问题描述

1.1问题背景

船厂钢板堆场管理流程具体描述为：1)根据生产计划汇总订单合同，钢板到达堆场后进入缓冲区堆放，按分段、尺寸等属性分类，等待入库操作；2)确定入库序列，桥吊空闲时依次从缓冲堆取出钢板移入堆场指定垛位，存储在主堆场中；3)确定出库集合，按出库计划从指定的位置取出目标钢板，若目标板在顶层，则直接移至预处理临时垛位并转5)，否则转4)；4)目标板上积压有其他钢板，为倒垛集合中的钢板选择然后移至新的存储垛位，直到目标板暴露在顶层，取出钢板并移至预处理临时垛位；5)在截止时间前依次将经过预处理的钢板放置在出场传送带上，组合出库。

主堆场中的钢板堆放限制条件包括：规格较大钢板不能压在小钢板之上；属性(包括分段号、终端用户、交货地、厚度、材质强度等级)相同或接近的钢板放置在同垛；垛位累积不能超过最大高度；每个垛位只能放置同一天出库的钢板[7]。基于本文研究的堆场布局，假设当前堆场以混合存储方式堆放大量钢板，以此为初始状态。如图1所示，建立堆场坐标，X/Y分别代表垛位列/行编号顺序：

1)主堆场垛位数量Y=RC，堆场以左上角为坐标原点，由一个桥吊承担出入库搬运作业；

2)钢板从左端缓冲堆入库，进入堆场后由起始坐标搬运至预分配垛位；

3)堆场每行(列)按照出库日期及尺寸划分，不考虑分段属性。从坐标原点开始，随着横(纵)坐标增大均匀分布；

4)钢板可以在不同行(列)之间进行倒垛优先选择同列不同行，桥吊主体梁横向(或起重小车纵向)移动，且只考虑单张钢板搬运；

5)假设堆场起始状态不为空，且以现有方式存储了一定量的钢板，并设垛位坐标Pi(Ci,Ri),(i=1,2,…,Y)

图1 堆场布局Fig.1 Layout of stack yard

混合存储情况下，堆场垛位分割只考虑尺寸和出库日期属性，针对分段的特殊属性再进行后续出入库方案优化。因此从预分配的角度，按照全部钢板的尺寸大小概率分布，以均衡各个垛位钢板数量为主要目的进行区域划分。如图2，堆场按尺寸界限值：下限(L,W)d=(Ld,Wd)，上限(L,W)u=(Lu,Wu)划分为Ar块区域，每个区域按照出库日期D依次分配垛位。

图2 堆场划分Fig.2 Stack yard division

假设造船厂全部入库钢板尺寸分布服从概率函数f(l,w):

(1)

(2)

式中：l和w分别代表钢板属性长和宽，Y为堆场垛位总数，μ为概率均值。式(1)为任意垛位i尺寸范围概率，表示累计垛位i尺寸范围内出现的概率；堆场垛位布局预划分时计算式(2)[8]，为保证堆场中各个垛位钢板数量分布均衡，以概率方差Δf值为控制变量，不超过指定最大值时可保证分布均衡。根据式(1)计算的频率，式(2)计算频率方差，方差越小，各个垛位钢板数量在概率上保证相近。从管理者角度来看式(1)、(2)，可以确定划分界限，防止堆场划分界限造成堆场运行管理过程中，部分区域钢板密集，垛位过高。同时按规则划分存储区域也便于出库时可按照尺寸和出库日期快速锁定所在垛位范围，能够加快查找速度，降低搜索算法的运行空间。

1.2出入库作业流程

对于造船厂，入库作业即为到货钢板安排合理垛位，出入库日期确定的前提下，入库钢板应尽量避免将出库日期临近的带分段属性板积压在下层，引起大量不必要的倒垛。由于钢板的分段属性，无分段板只需满足订单数量规格要求，带分段板须按分段先集齐段位后组合出库。因出库方式不同，所以出库作业分两种：1)取出符合出库要求规格和数量的钢板；2)从指定位置取出入库前作特殊分段号标记的钢板集合。

根据在库板存储限制条件和本文研究问题的特殊性提出以下入库规则：钢板分段号、尺寸大小及材质>出库日期>垛位高度.按堆场放置原则逐个选择，放置在垛位最上层，不进行预倒垛。

出入库作业和堆场状态变化之间相互关系如图3所示。

图3 钢板出入库流程Fig.3 Logical flow of steel plate inbound and outbound

为解决本文混合存储出入库组合优化问题，合理安排钢板进入堆场的次序，为钢板预分配存储空间，优化出库分配计划，建立整数规划模型。

2 数学模型

2.1堆垛及倒垛约束模型

设垛位t中钢板的最大尺寸为Lmax t，最小尺寸为Lmin t，根据现有的船厂钢板堆场管理信息系统，入库钢板在到达堆场前7、8 d就对堆场发出预约垛位信息，按分段号将订单汇总分类整理。为防止同一垛位钢板尺寸不同，会造成相互积压变形，增加矫正工序，必须降低同一垛位钢板尺寸差异，因此建立以下约束模型。全部钢板包括指定分段和不指定分段属性钢板入库选择垛位时都需要满足以下尺寸约束，降低同一垛位钢板尺寸偏差。同理，倒垛即为出库目标板以上的钢板集合重新选择垛位[9]。z为初始设定值，同一个垛位钢板的长度宽度之差约束如下，j/k为垛位t中任意两块板。rij/cij为出库板i对应出库集合中板j所在行/列，Xij=1表示钢板j选为出库Pij对应板，Xij=0时则反之，i=1,2,…,M；Xijr：代表出库板i对应板j所在垛位第r层钢板，存在时为1。限制垛位相邻两块板宽度(长度)差在一定范围内：

|Wj-Wk|≤Wm+(2-Xijr-Xikr-1)Z

(3)

|Wj-Wk|≤Wm+(2-Xijr-Xikr+1)Z

(4)

|Lj-Lk|≤Lm+(2-Xijr-Xikr-1)Z

(5)

|Lj-Lk|≤Lm+(2-Xijr-Xikr+1)Z

(6)

为保证垛位内任意两块板与垛位内最大板长度差在一定范围内,则

(7)

(8)

r=1,2,…,Hm

目前对于倒垛作业优化的研究已经较为成熟，倒垛模型假设选择的垛位大部分都是在原垛位附近，以加快算法运行速度降低问题复杂度，重新选择的垛位满足以上垛位尺寸约束同时还要满足：

(9)

图4 相邻可倒垛位分布Fig.4 Distribution of neighbored shuffling stack

2.2目标函数及约束

根据问题约束和优化目标建立数学模型，Dij为出库板i对应钢板j翻板数量，优化目标为最小化桥吊翻板及运输所需钢板行驶的时间为

(10)

完成板i出库作业需要的操作时间为

(11)

式中：tc为桥吊横向移动单位距离时间，t0代表桥吊取板上下移动时间，ts桥吊倒垛平移时间；tu桥吊倒垛上下移动时间。

取出(i-1)块板后，第i块板预计倒垛量：

Dij=max{Dj-max{Xij,Dj+1|I′=

(12)

在出入库作业全过程中，计算出桥吊行驶距离成本为

(13)

为取出出库板i对应符合条件的板j的付出的倒垛成本公式为

(14)

每一个垛位中钢板堆放的总高度限制为

(15)

限制钢板出库时间在其上倒垛板完成倒垛之后作业时间为

(16)

保证对应出库序列中无分段板有符合要求数量的板、带分段板有且只有一块板被选作目标板，则：

(17)

(18)

由以上描述及模型可知问题属于多目标组合优化问题[10]。为求解该问题，本文将改进现有方法，针对可行解空间大而难以找到最优解的问题，提出基于模拟退火概率接受准则的两层嵌套遗传算法，通过出库作业内层解对外层入库作业计划的动态适应，求解研究周期内堆场物流周转方案。这种算法具有特殊问题适应性，从而更能找到本文提出的混合存储优化问题的较优解。

3 模拟退火双层遗传算法

3.1编码方式

本文提出基于模拟退火概率接收准则的两层遗传算法来解决文中的问题，设Ei为入库清单整合规格序列Ei{e1,e2,…,ei,…,eM}，M为出库计划中钢板总数，钢板出库序列P=(P1,P2,…,PM)，Ωt堆场在研究周期T状态，出库计划中的第i个钢板Pi的规格参数为ei=(Li,Wi,Hi,Gi,Seg,Ni)，分别对应长、宽、厚、材质、分段号、需求数量，不指定分段板Seg值为空，编码方式如下所述：

图5 入库编码Fig.5 Inbound coding mode

2)堆场状态Ω编码以及内层选择匹配组合出库编码，若堆场内钢板以数组堆栈存储，E[i][k](i∈[1,Y],k∈[1,Hm])。将符合规格ei的板设为i×10+1，十位以上为外层染色体出库次序编号。无板层设为0，有板层设为1，堆场可数字化为表1所示。

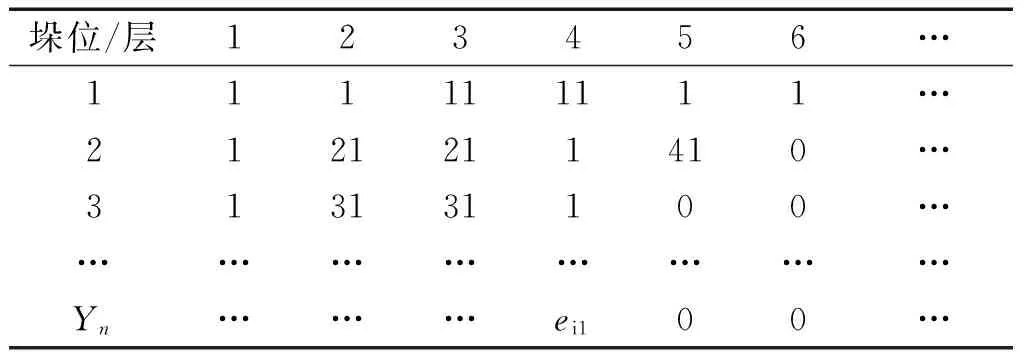
表1 堆场垛位数字化编码

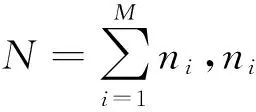
图6 出库组合编码Fig.6 Outbound combining coding mode

4)倒垛按步骤3染色体中为1的基因位确定目标板集合。倒垛集合也随之确定，为每块倒垛板建立可倒垛位集合。对于集合中每一个垛位，通过移动堆场状态编码中原位置和新位置的值反映钢板移动。每次移动令累积倒垛次数(shuffling number)SN=SN+1，最终在可倒垛集合中选择为完成该板出库作业预估倒垛量(SN值)最小的垛位组合。

另一方面，本文采用的对比算法为一般遗传算法，编码方式采用以上两层染色体拼接为一条染色体的方式，如图7所示。

图7 GA染色体编码Fig.7 GA chromosomecoding mode

3.2算法流程

本文采用的基于模拟退火两层遗传算法进行优化求解，其中选择策略是基于模拟退火的概率接受准则，可降低内层算法对外层解的模糊化，采用概率接受准则增加种群原始解的保存率，防止内层算法对外层基因的破坏。具体算法流程如图8所示。

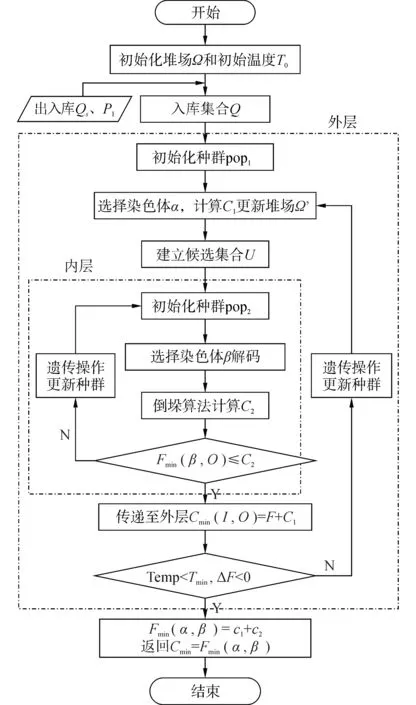
图8 模拟退火双层遗传算法流程Fig.8 SA-HGA algorithm flow

4 实例验证与数值分析

4.1参数设置

为证明上面提出的算法在该问题背景下的实用性和有效性，采用实例验证算法可行性并与一般遗传算法性能作对比。算法是在Windows7系统下基于Matlab2011b实现，选取某大型造船厂实际数据验证，当前研究的是在堆场状态不为空的情况下一个调度周期内出入库作业计划。表2是实例数据以及参数基准单位设置。

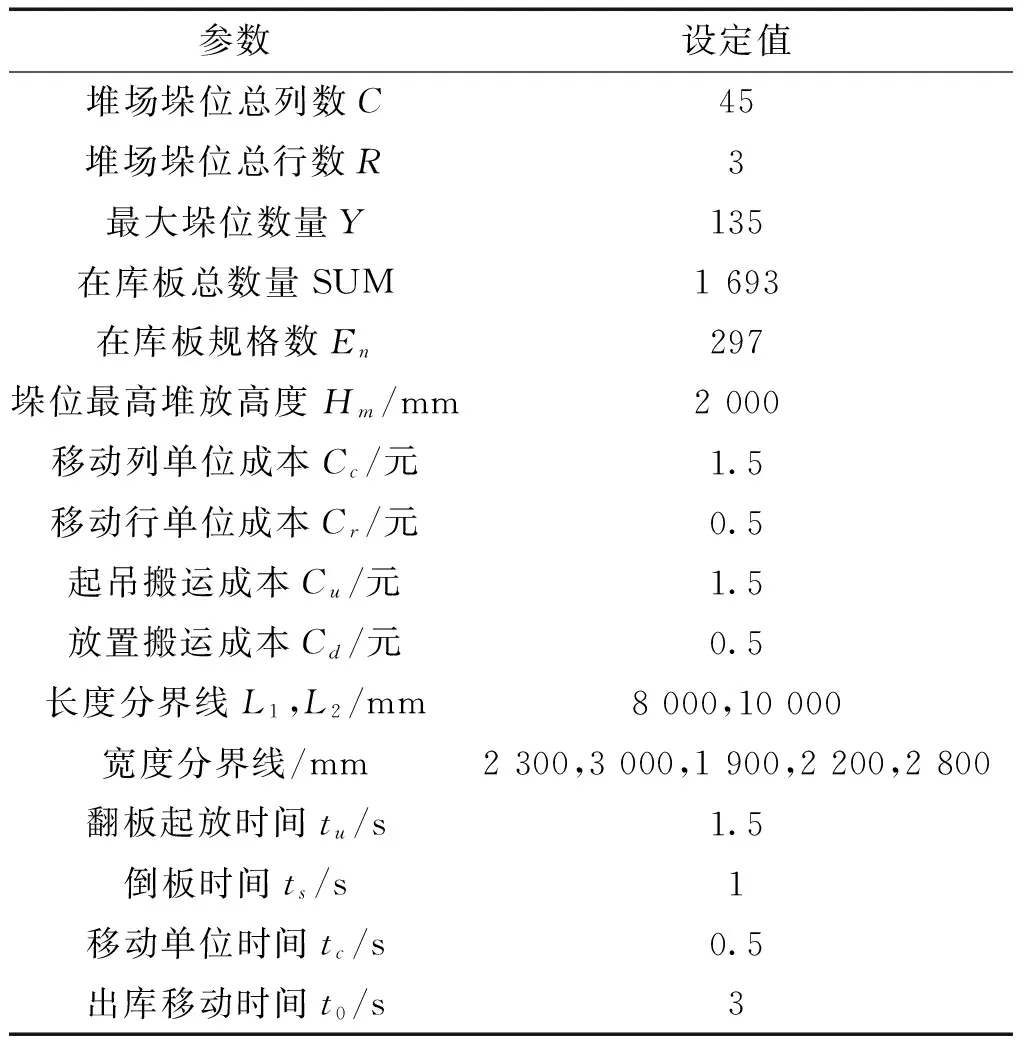
表2 初始参数设置

遗传算法的参数设置在文献中有相关研究，根据文献[10-12]，为保证种群多样性增加变异概率，根据实验后的种群收敛性确定，基于模拟退火概率接受准则的双层遗传算法参数选择为：外层迭代次数NC1=100，种群大小N1=20，内层迭代次数NC2=50次，种群大小N2=30，内外层选择比例GAP=0.8，交叉概率为XOVER=0.7，变异概率MUTR=0.2。

为了验证并与本文算法进行对比，GA算法的参数选取为：迭代次数NC=100，种群大小N=50，选择比例GAP=0.8，交叉概率XOVER=0.7，变异概率MUTR=0.2。

4.2实例验证与分析

表3显示混合存储在出入库规则约束下，对目标函数无明显影响。是由于堆场空间利用率的影响，因此表4数据证明了混合存储方式在规则约束下的可行性。

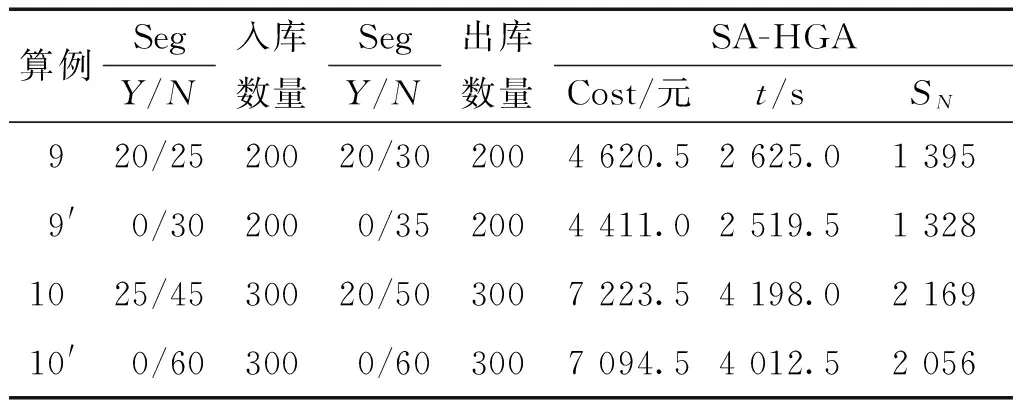
表3不指定分段与混合存储算例对比数据

Table3Datacomparisonbetweenmixedstorageandnon-segmentedstorage

算例SegY/N入库数量SegY/N出库数量SA-HGACost/元t/sSN920/2520020/302004620.52625.013959'0/302000/352004411.02519.513281025/4530020/503007223.54198.0216910'0/603000/603007094.54012.52056

注：Y、N分别是指定分段和不指定分段；Cost为完成出入库倒垛作业所需的人工设备总成本；SN为倒垛量。

表4 混合存储不同规模算例数据

表4分析了随入库钢板数量，包括指定分段和不指定分段板同步增加时堆场运行代价的变化趋势。考虑到部分指定分段钢板混合存储在堆场中，出库时不仅有出入库钢板相互堆叠[11]形成倒垛作业的增加，更有指定分段和不指定分段板之间相互堆叠，因此调度方案优化方向为避免取出指定分段板时对积压在其上的其他分段属性钢板大量移动。表4中对比数据可以看到，对于算例1和2，在钢板数量较少时两个算法都能求得最优解。当钢板出入库的规格种类数较多，移动总数量超过200时，比如算例10，运输成本和时间急剧增加，GA不能完成作业优化，而SA-HGA算法则可以对两层操作进行动态协调，找到令出库组合最优的入库方式，同时得到与之相适应的倒垛和出库作业计划，使得出库作业高效且控制成本。本优化算法得到的作业方案，明显优于GA得到的作业方案。以算例8为例，应用本算法，倒板数量减少13.4%，桥吊作业成本减少14.1%，作业时间缩短10.1%。

为验证算法有效性，算法求解优化模型需要的时间随问题规模变化曲线如图9所示。由于本文采用的双层嵌套遗传算法运行时间比一般遗传算法运行时间稍慢，但也在实际堆场作业管理可接受范围内，因此算法是可行且有效的。

以算例9为例，进一步将两种优化算法的收敛性[12]作对比。SA-HGA内外层目标函数变化曲线如图10所示，可以看到算法运行时表现出较好的收敛性。

图9 算法运行时间随问题规模变化曲线图Fig.9 Algorithm running time with variable problem scales

图10 SA-HGA和GA 算法收敛性对比Fig.10 Convergence performance of SA-HGA comparison to GA

由于遗传操作的局限性，一条同时携带出入库计划方案的染色体可能会同时在多个位置发生变化，容易破坏解的质量甚至陷入早熟收敛。而与传统的遗传算法相比，采用模拟退火概率接受准则的双层遗传算法对内外层染色体协调优化，出入库作业方案相互配合，保证了外层较优解的持久度，而遗传操作同时不断更新种群，防止早熟收敛。因此从表4及图10可知，传统遗传算法收敛性较好，能较快寻得较优解。

5 结论

1)提出了基于堆场当前状态，带分段属性和无分段属性两类钢板混合存储的方法，针对本文提出的多目标组合优化问题，建立了整数规划模型，进一步优化出入库作业成本和时间；

2)为适应于该多约束组合优化问题，提出运用模拟退火双层遗传算法优化作业计划，通过算法实例演算结果表明，算法能在一定的迭代次数内寻得较优解；提供堆场管理作业方案，大幅度降低堆场作业成本和时间、减少倒垛量并且具有较高的规模适应性。并与GA相比较，证明本文提出SA-HGA的可行性和有效性。

本文尚需完善堆场空间利用率的计算，同时也为两类分段板的存储方式研究提供了新的方向。

[1] 施敏, 徐端, 刘宇晶. 垛位自动预约技术在宝钢船板配送中心库场管理系统中的应用[J]. 冶金自动化, 2011(6): 28-32.

SHI Min, XU Duan, LIU Yujing. Applications of pile automatic appointment in BaosteelShip distribution center[J]. Metallurgical industry automation, 2011(6): 28-32.

[2] 徐萍. 造船厂钢板入库作业优化及钢板管理信息系统开发[D]. 镇江: 江苏科技大学, 2011.

XU Ping. Optimization on input operations and management information system development of a steel plate stacking yard in a shipyard[D]. Zhenjiang: Jiangsu University of Science and Technology, 2011.

[3] 蒋如宏, 钟宏才, 谭家华. 船厂钢板堆场管理的数字化仿真[J]. 上海交通大学学报, 2003, 37(8): 1242-1245.

JIANG Ruhong, ZHONG Hongcai, TAN Jiahua. Simulation of digitized plate stockyard management in shipyards[J]. Journal of Shanghai Jiao Tong University, 2003, 37(8): 1242-1245.

[4] 刘建峰, 张小辉, 蒋志勇,等. 基于遗传算法入库钢板分配策略研究[J]. 江苏科技大学学报:自然科学版, 2011(6): 524-529.

LIU Jianfeng, ZHANG Xiaohui, JIANG Zhiyong, et al. Allocation strategy of steel plate in store house based on genetic algorithm[J]. Journal of Jiangsu University of Science and Technology: natural science edition, 2011(6): 524-529.

[5] 唐立新, 杨自厚. 热轧实施计划中最优倒垛问题的整数规划模型及遗传算法[J]. 自动化学报, 2000, 26(4): 461-469.

TANG Lixing, YANG Zihou. Integer programming model and modified genetic algorithm for optimalturned-out slab pile for hot rollinne schedule[J]. Acta automatic sinica, 2000, 26(4): 461-469.

[6] 李耀华, 王伟, 胡国奋, 等. 热轧板坯库出库计划编制模型与算法研究[J]. 计算机集成制造系统, 2006, 12(3): 377-381.

LI Yaohua, WANG Wei, HU Guofen, et al. Research on slab discharge planning model and algorithm for hot-rolling slab-yard[J]. Computer integrated manufacturing systems, 2006, 12(3): 377-381.

[7] ZHAO R, TANG L. Integer programming model and dynamic programming based heuristic algorithm for the heavy plate shuffling problem in the Iron and steel industry[C]// International Conference on Logistics Systems and Intelligent Management. 2010: 1381-1385.

[8] ZHANG Z, WANG P, WANG W. Optimization and operation scheduling for a steel plate yard based on greedy algorithm[J]. Journal of networks, 2013, 8(7):1654-1659.

[9] TANG L, REN H. Modelling and a segmented dynamic programming-based heuristic approach for the slab stack shuffling problem [J]. Computers & operations research, 2010, 37(2): 368-375.

[10] 王广民. 造船厂钢板堆场出库作业计划建模及优化研究[D]. 大连: 大连理工大学, 2009.

WANG Guangmin. Modeling and optimization on operation scheduling of a steel plate stacking yard in a shipyard[D]. Dalian: Dalian University of Technology, 2009.

[11] 张志英, 王维泽, 侯俊. 船厂钢板堆场多时段作业计划优化[J]. 哈尔滨工程大学学报, 2015(5): 638-643.

ZHANG Zhiying, WANG Weize, HOU Jun. Optimization of multistage operation scheduling for a steel plate stockyard in shipbuilding[J]. Journal of Harbin Engineering University, 2015(5): 638-643.

[12] WANG G, JIN C, DENG X. Modeling and optimization on steel plate pick-up operation scheduling on stack yard of shipyard[C]//IEEE International Conference on Automation and Logistics, 2008: 548-553.

本文引用格式：

侯俊，张志英. 船厂钢板堆场混合存储分配及出入库调度研究[J]. 哈尔滨工程大学学报， 2017， 38(11): 1786-1793.

HOU Jun, ZHANG Zhiying. Location allocation for inbound and outbound scheduling of mixed storage steel plate in shipyard[J]. Journal of Harbin Engineering University， 2017， 38(11): 1786-1793.

Locationallocationforinboundandoutboundschedulingof
mixedstoragesteelplateinshipyard

HOU Jun, ZHANG Zhiying

(School of Mechanical Engineering, Tongji University, Shanghai 200092, China)

To meet with the principle of managing shipyard that the steel plate in the stack yard is partly characterized by the block numbers and hybrid storage, this paper firstly verified that the assumption of mixed storage of block-oriented plates is feasible, and at the same time, optimized the shuffling costs followed by the outbound and inbound operations, and realized the purpose of reducing the costs including logistics and operation time of the processes, thereby improving the utilization of the stockyard. An integer programming model was formulated, and the approximately optimal solution was obtained according to the hierarchic genetic algorithm based on the simulated annealing probability accepted criterion (SA-HGA), programming the operation of pre-allocating for the two kinds of inbounding plates based on the current storage state, making sure that the plates inbounding is equally distributed, providing shuffling and out bounding plans according to the demand which costs less budget and time. At last, it′s proved that the algorithm is of convergence and effectiveness by analyzing several cases, which are of different scales and make a contrast to the general genetic algorithm (GA). The results of the numerical experiments demonstrate the assumption and make an improvement to the operation plan of 4.9%～21.3% in cost and 7.6%～10.1% in operation time.

shipyard; stockyard; segment; steel plate operation scheduling; hierarchic genetic algorithm; simulated annealing

10.11990/jheu.201606059

http://www.cnki.net/kcms/detail/23.1390.u.20170427.1544.150.html

TP18，U673

A

1006-7043(2017)11-1786-08

2016-06-21.

网络出版日期：2017-04-27.

国家自然科学基金项目(70872076);上海市科技创新行动计划项目 (11DZ1121803);江苏省南通市2010AA科技创新计划(工业)基金项目(AA2010048).

张志英(1971-), 男, 副教授.

张志英, E-mail:zyzhang08@tongji.edu.cn.