改进模拟退火遗传算法在协同空战中的应用
宋遐淦, 江驹, 徐海燕
(1.南京航空航天大学 自动化学院,江苏 南京 211106; 2.南京航空航天大学 经济与管理学院,江苏 南京 211106)
改进模拟退火遗传算法在协同空战中的应用
宋遐淦1, 江驹1, 徐海燕2
(1.南京航空航天大学 自动化学院,江苏 南京 211106; 2.南京航空航天大学 经济与管理学院,江苏 南京 211106)
针对不确定环境下的目标分配问题,本文建立了相应的评估及分配模型。构建空战态势评估指标体系,并用区间层次分析法(interval analytic hierarchy process, IAHP)和模糊优选法确定指标的主客观权重。然后建立相应的不确定环境下多目标优化攻击效能评估模型,将协同多目标攻击决策问题转化为导弹攻击配对优化问题。进一步提出一种基于区间灰数的模拟退火遗传算法(interval grey number-simulated annealing genetic algorithm, ISAGA)用于该决策问题的求解,设计了选择操作和相应的模拟退火机制,有效防止算法陷入局部最优。最后根据寻优所得的解确定合理的攻击方案。仿真结果表明:所提出的算法可以胜任不确定环境下目标分配问题的评估和寻优,并且在10步以内能够找到比较好的解,这在一定程度上是对传统的目标分配问题的完善。
区间层次分析法; 可能度函数; 区间灰数; 区间遗传算法; 模拟退火; 协同空战
协同多目标空战主要包括战场环境评估和火力分配两个方面。战场环境评估是指根据战机本身的空战能力和空战态势计算出敌方编队战机对我方战机的威胁评估矩阵。火力分配是指根据作战目的、战场态势和武器性能等因素,将一定类型和数量的火力单元以某种准则进行分配,攻击一定数量敌机的过程[1-2]。
战场环境评估问题国内外已经有大量研究,算法也相对成熟,如层次分析法、逼近理想排序法[3]等。考虑在实际空战中,某些信息的不确定性,一些学者针对这些“柔”性信息将传统的威胁评估方法进行了推广,提出了基于区间的改进的评估方法[4-5]。然而目前大多研究仅获得基于区间的威胁权重,在应用到协同多目标空战中时并不能给出进一步导弹分配的攻击方案。
目标分配问题属于一类NP-hard问题。国内外研究以对目标杀伤最大化为目的,采用智能优化算法,如启发式遗传算法[6]、模拟退火遗传算法[7]、蚁群算法[8]、粒子群算法[9]等对模型进行求解。在智能优化算法改进方案[10-11]的研究中,虽然改进后的智能优化算法的快速收敛性和寻优能力有了一定的提高,但是仍然无法处理威胁评估后的不确定信息。
1982年,邓聚龙教授创立的灰色系统理论[12],是一种基于少数据、贫信息不确定环境下决策的有效工具。本文为了更好地处理威胁评估结果,实现不确定环境下的空战目标分配,引入区间灰数来表征战场信息的不确定性,引入灰色系统理论中的“可能度”的概念很好地解决了灰区间比较的问题。通过设计合适的适应度函数、新的区间选择机制和模拟退火机制使遗传算法能胜任个体适应度为灰区间形式的寻优,在较少的迭代次数内能得到比较接近最优解的解。
1 基于区间灰数威胁评估指标权重的确定
现代超视距多目标空战中,目标威胁程度取决于战机本身的空战能力和空战态势[13]。参考文献[13]考虑先进四代机的低探测性和超机动性,因此在传统空战态势考虑因素的基础上作了一些修改,考虑角度、速度、距离、高度、隐身和空战能力因素。
本文参考现有研究成果,计算敌方战机编队每架飞机对我方战机编队每架飞机的优势值,最终构成威胁灰矩阵作为目标分配的依据。
在权重确定时考虑主观权重和客观权重两种情况。主观权重采用层次分析法(analytic hierarchy process, AHP)。但是传统AHP只能处理“刚”性信息,在构建判断矩阵时,决策者对于复杂环境下威胁因子的评估难以给出确定的偏好,更倾向于给出一个区间,因此采用区间层次分析法来处理瞬时空战态势中的“柔”性信息。客观权重采用模糊优选法。
1.1运用IAHP确定主观权重的步骤
为了描述信息的不确定性有必要引入灰色系统理论中区间灰数的概念。有学者提出把不知某一确切值但只知道其取值范围的数称为灰数,它是组成灰色系统的“单元”或“细胞”,常用符号“⊗”表示。
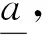
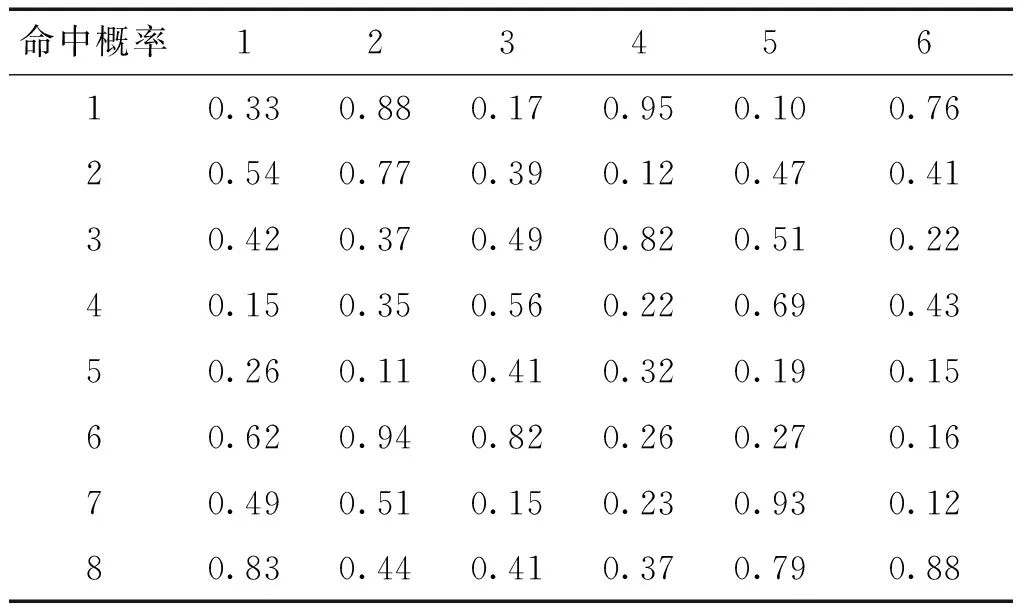
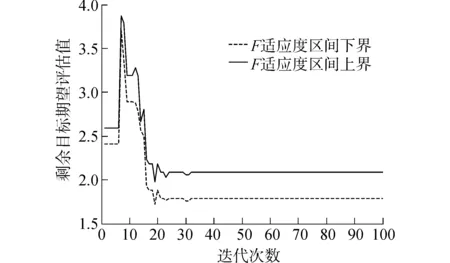
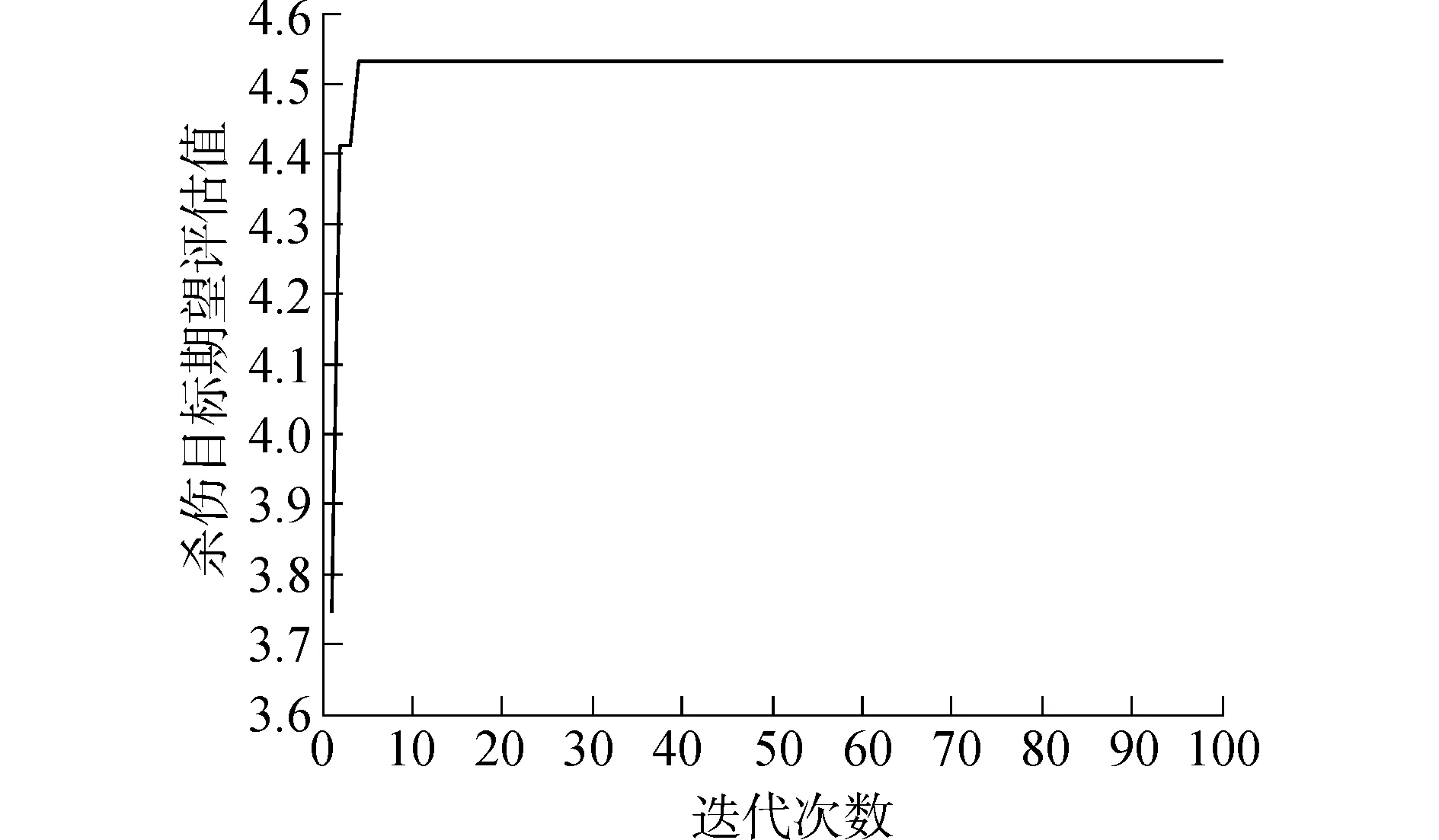
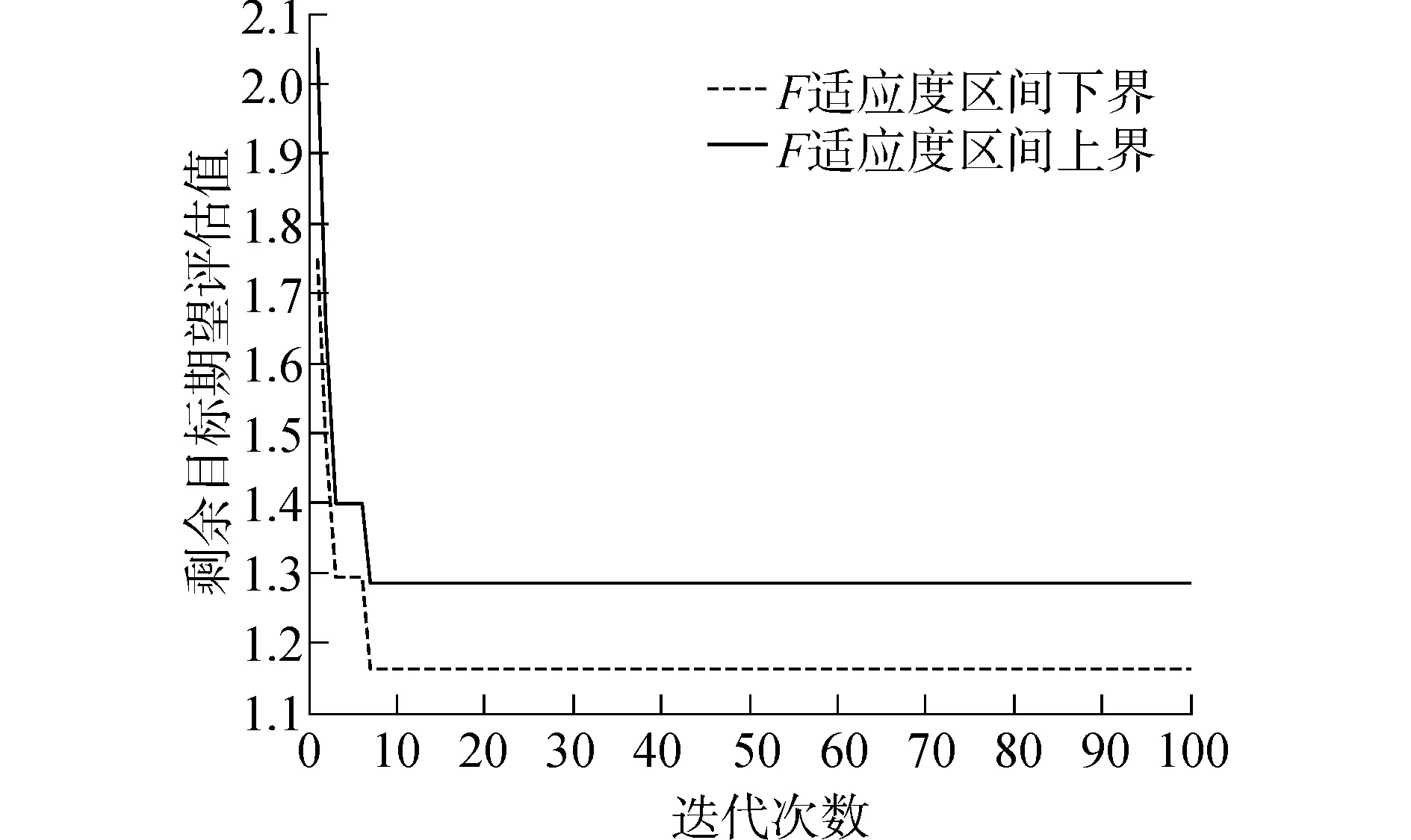
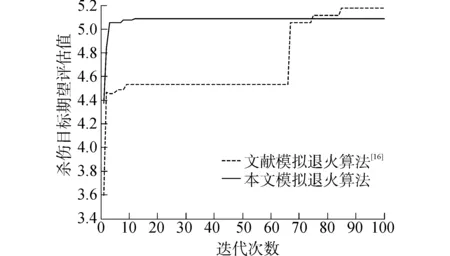
定义2区间灰数基本的运算法则如下:设⊗1∈[a,b],a 加法运算:⊗1+⊗2∈[a+c,b+d] 减法运算:⊗1-⊗2∈[a-d,b-c] 乘法运算: ⊗1·⊗2∈[min{ac,ad,bc,bd},max{ac,ad,bc,bd}] 除法运算: 其中,c≠0,d≠0,cd>0。 3)解算权重W=(w1,w2,…,wn)T,并归一化处理。 1.2运用模糊优选法确定客观权重的步骤 1)根据文献[13]中的威胁因子构造威胁评估矩阵F,矩阵F中的第i行第j列元素fij表示目标机j关于属性i的威胁度值。然后,进行无量纲化处理,得到新的相对威胁度评估矩阵μ 构造拉格朗日函数解算出模糊优选法确定的最终客观权重表达式: 3)将运用IAHP得到的主观权重区间和运用模糊优选法得到的客观权重进行综合计算,得到组合权重区间,即 ω=ηωs+(1-η)ωo (1) 式中:ωs、ωο分别为主、客观权重;η为主观权重影响因子,可根据对专家的信任程度确定,这个组合权重能比较全面地反映威胁评估的相对重要程度。 2.1空战决策问题数学模型的描述 通过上面的一系列步骤可以得到某一时刻敌机对我机的威胁灰矩阵T。另外,假设我方一个空战编队有m架飞机,每架飞机拥有ri枚导弹,敌机n架。首先对这m架飞机的导弹进行编号,m架飞机共有∑ri=r枚导弹,导弹编号为k。设pkj为第k枚导弹攻击第j个目标的毁伤概率。设xkj为决策变量,xkj=1表示分配第k枚导弹攻击第j个目标,xkj=0表示没有实施攻击,则可以建立如下协同多目标攻击空战决策模型: 目标函数: (2) 式中:目标一表示剩余目标的威胁评估函数值最小化,目标二表示尽可能多的毁伤空战目标。 约束条件: (3) 式中:约束条件一表示最多可以分配sj枚导弹攻击第j个目标。约束条件二表示最多可使用r枚导弹。约束条件三表示一枚导弹不能同时攻击两个和两个以上的目标。 文献[14]采用线性加权法将多目标优化转化为单目标优化,另外采用罚函数法来处理约束条件,得到最终的简化后的目标函数模型: minω1F+ω2(n-E)/n+ (4) 式中:N为惩罚因子,用来对解空间中出现攻击两个目标以上的情形进行“惩罚”。 2.2可能度函数的描述 本文采用基于区间灰数的遗传算法来解决多目标空战的寻优问题,由于目标函数中的威胁矩阵是一个灰矩阵,目标函数计算出来的适应度值必定是灰区间而不是“刚性”点数值。 但是区间灰数的排序问题至今研究比较少[15],有必要寻求一种新的适用于区间灰数的排序方法作为遗传算法选择操作的理论依据。 定义3设a为任意实数,⊗∈[⊗-,⊗+]为任意区间灰数,则称 为实数a小于区间灰数⊗的点可能度函数。 定义4⊗1∈[⊗1-,⊗1+],⊗2∈[⊗2-,⊗2+]为任意两个区间灰数,⊗(γ)为区间灰数标准化形式。若γ1是给定的,则p(⊗1(γ1)<⊗2)为固定点⊗1(γ1)小于区间数⊗2的可能度函数,那么称 ⊗1(γ1)<⊗2)dγ1 为区间⊗1小于区间⊗2的可能度函数。并且满足“互补性”,即p(⊗1≥⊗2)=1-p(⊗1<⊗2) 通过可能度函数的定义,可以很方便地描述某个区间相对于另一个区间“大”或者“小”的程度,因此非常适合多个灰区间的相互比较。 2.3空战决策问题数学模型的修正 考虑到以下两种情况: 1)从耗弹量的角度考虑,某些分配方案耗弹量少但是目标函数计算出的适应度值相差不大,这时需要进行相应的“奖励”。 2)从机载导弹发展的角度考虑,随着导弹技术的发展,未来机载导弹可以同时攻击多个空中目标,此时需要对模型进行改进。引入变量Si为一枚机载导弹最多可以攻击的目标数量。 将式(4)记为E0,对目标函数作如下修正,修正后的目标函数为 (5) 式中:M为导弹攻击目标超过Si的惩罚因子,P为弹药节省的奖励因子。 设种群个体数量为N,规定迭代次数M,交叉概率为pc,变异概率为pm。为了提高搜索效率,首先产生N个满足约束条件的初始解X0。利用初始解根据式(5)计算粒子的适应度值为 当(迭代次数小于规定的迭代次数) 初始化种群 1)编码 采用二进制编码,解是以矩阵形式给出,只要给出我方导弹总数量r和敌机数量n就可以用二进制矩阵的形式表示出分配方式。 2)选择操作 以f(⊗01)为基准,分别计算其他适应度值灰区间相对于f(⊗01)的可能度函数值,并以此为依据用轮盘赌的方式进行遗传算法选择操作。如有三个灰区间分别为 [0,1]、[0.5,1.5]、[2,3],根据式(5)可以计算出⊗1>⊗1、⊗2>⊗1、⊗3>⊗1的可能度为分别为0.5、0.875、1。为了使优良的个体更容易被选择,可以进行N轮回的比较,将每轮比较后得到的可能度值进行积累。在第二轮比较中可以得到⊗1>⊗2、⊗2>⊗2、⊗3>⊗2的可能度分别为0.125、0.5、1。第三轮⊗1>⊗3、⊗2>⊗3、⊗3>⊗3的可能度分别为0、0、0.5。最终的可能度积累可以用优势积累矩阵C来表示: Cij表示第i个灰区间与第j个灰区间的比较结果,分别计算列和得到三个灰区间的累积适应度值分别为0.625、1.375、2.5。用“归一法”得到最终的三个个体被选择的概率分别为0.137、0.315、0.548。本文采用联赛制多轮比较将每个个体与其他个体比较后得到的可能度进行累加,最终的累加值作为选择操作评判依据。 3)交叉操作 交叉操作是采用单点交叉的方式。先产生一个随机数r,假如r 4)变异操作 先产生一个随机数r,假如r 5)模拟退火操作 首先确定当前种群最佳个体,找出最佳染色体并通过个体得到新个体。 产生新个体方法:在最佳个体的基础上随机选取两行进行交换,然后随机选取两列进行交换,这样交换后的解依然是可行解。 定义初始温度T0及系数γ⊂(0,1), 当(T0>Tmin)时 计变异操作后的最佳个体P0,产生的新个体P1。计算适应度值Fit(P0)和Fit(P1) 在本文中,p(Fit(P1) 反之,则以概率p=exp(-ΔF/T)接受劣质个体,其中ΔF=Fit(P0)+-Fit(P1)-。 T=T×γ,判断是否T 4.1仿真1 设我方的一个4机编队与敌方的6架飞机进行空战,假设每架飞机携带两枚导弹。规定每个目标最多收到两枚导弹的攻击。显然分配方案是一个48维的离散0-1空间。设初始种群个体的数量设为40,迭代次数设为100,式(6)中两个目标的权重ω1和ω2设为0.6和0.4。罚因子N设为100,罚因子M设为100。奖励因子P设为0.001。8枚导弹对6个目标的命中概率矩阵见表1,6个目标对我方4个目标的威胁值灰区间矩阵见表2(综合威胁评估)。 表1 导弹对目标的命中概率 表2 目标对我机的威胁值灰矩阵 采用区间灰数模拟退火遗传算法对该算例进行仿真。每次均能快速收敛,其中一次仿真,未引入模拟退火算法仿真中综合最佳适应度期望值,剩余目标期望值F评估值E的进化曲线如图1~3所示。可以看到未引入模拟退火时算法收敛性一般,大概在25代左右得到本次运行的最优解。 引入模拟退火算法仿真后综合最佳适应度期望值,剩余目标期望值F和杀伤目标期望评估值E的进化曲线如图4~6所示。 图1 综合最佳适应度期望值变化曲线(未引入模拟退火)Fig.1 Curves of the comprehensive best fitness (without SA) 图2 F变化曲线(未引入模拟退火)Fig.2 Curves of F(without SA) 图3 E变化曲线(未引入模拟退火)Fig.3 Curves of E(without SA) 图4 综合最佳适应度期望值变化曲线(引入模拟退火)Fig.4 Curves of the comprehensive best fitness(with SA introduced) 图5 F变化曲线(引入模拟退火)Fig.5 Curves of F(with SA introduced) 结果分析: 1)引入模拟退火后算法的快速性和收敛性变得很好,在十代左右就可以得到一个理想值。 2)由于“可能度”的引入使得最终得到的最佳适应度值和剩余目标评估值E以区间形式给出,仿真中用两条曲线分别来表征最好和最坏的情形。 3)本次运行的可行解为X: 由矩阵X可知,第1枚导弹攻击目标4,第2、3枚导弹攻击目标1,第4、5枚导弹攻击目标3,第6枚导弹攻击目标2,第7枚导弹攻击目标5,第7枚导弹攻击目标6。此时最佳适应度值区间为[0.809 3,0.860 2],剩余目标期望值F的区间为[1.247 5,1.332 3],杀伤评估值E为5.088 4。 4.2仿真2 仿真1只是检验了本文所提出算法的有效性,其性能优劣还需与其他智能算法进行对比才能得出结论。由于其他智能算法并不能解决不确定环境下的目标分配问题,在此将仿真1中设置的情景进行简化,将目标对我机的威胁值灰矩阵简化为常值矩阵;仿真2中威胁值矩阵中各元素值均取仿真1中威胁值矩阵中各灰区间左侧的值,其他参数设置均相同。 文献[16]中作者设计了模拟退火遗传算法用于协同多目标攻击决策问题的寻优,与本文不同的是算法中个体采用整数编码,并采用非常规的交叉与变异操作产生新的个体,具体操作过程在此不再赘述。将文献[16]所设计的算法用于本文多目标攻击决策问题的寻优,杀伤目标期望评估值E的进化曲线如图7所示。 图7 E变化曲线对比图Fig.7 Comparison curves of E 结果分析: 1)用文献中给出的模拟退火遗传算法解决本文协同多目标攻击决策问题,最终得到了比本文所采用的算法更好的解。因此,文献提出的算法的搜索准确性要优于本文所提算法。 2)可以初步断定算法的搜索效率和搜索准确性与编码方式有一定的关系,倘若只强调搜索准确性,则优先考虑十进制编码,倘若只强调搜索快速性,则优先考虑二进制编码。但是,算法性能也与交叉与变异操作方式有一定关系,要弄清楚交叉与变异操作方式对算法性能影响的大小还有待深入研究。 3)空战中态势瞬息万变,要想在有限时间内得出当前态势下最优的分配方案往往是很困难的,本文所提出的算法虽然没有得到最优的分配方案,但是在较少的时间内得到了比较满意的解,这也是可以被决策者接受的。 1)本文所提出的算法能适应个体适应度为灰区间形式的寻优,可以作为传统确定环境下目标分配问题的补充和完善。 2)在不确定环境下,引入模拟退火算法后,遗传算法的收敛性和快速性都能得到有效提高。 3)本文所提出的算法虽然没有得到最优的分配方案,但是在较少的时间内得到了比较满意的解,这也是可以被决策者接受的。 如何进一步提高算法的实时性,使之能运用于武器火控系统是下一阶段的研究内容。 [1] 罗德林,吴顺祥,段海滨,等. 无人机协同多目标攻击空战决策研究[J].系统仿真学报, 2008, 20(24): 6778-6782. LUO Delin, WU Shunxiang, DUAN Haibin, et al. Air-combat decision-making for UAVS cooperatively attacking multiple targets[J]. Journal of system simulation, 2008, 20(24): 6778-6782. [2] 董朝阳,路遥,王青. 改进的遗传算法求解火力分配优化问题[J].兵工学报, 2016, 37(1): 97-102. DONG Chaoyang, LU Yao, WANG Qing. Improved genetic algorithm for solving firepower distribution[J]. Acta armamentarii, 2016, 37(1): 97-102. [3] WILLIAM P F. Ranking terrorist targets using a hybrid AHP-TOPSIS methodology[J]. The journal of defense modeling and simulation, 2016, 1(13): 77-93. [4] WU Qunli, PENG Chenyang. Comprehensive benefit evaluation of the power distribution network planning project based on improved IAHP and multi-level extension assessment method[J]. Sustainability, 2016, 8(8): 796. [5] XU Long, LI Yi. A network selection scheme based on TOPSIS in heterogeneous network environment[J]. Journal of Harbin Institute of Technology, 2014, 1(21): 43-48. [6] 张毅,姜青山.基于模糊-灰色非合作Nash博弈的多组动态武器-目标分配方法[J]. 云南大学学报, 2012, 34(1): 26-32. ZHANG Yi, JIANG Qingshan. An approach of basing-on fuzzy-grey noncooperative nash games to multi-team dynamic weapon-target assignment[J]. Journal of Yunnan University, 2012, 34(1): 26-32. [7] ASIM T,SEROL B. Weapon target assignment with combinatorial optimization techniques[J]. International journal of advanced research in artificial intelligence, 2013, 2(7): 39-50. [8] WANG Yanxia, QIAN Longjun. Weapon target assignment problem satisfying expected damage probabilities based on ant colony algorithm[J]. Journal of systems engineering and electronics, 2008,19(5): 939-944. [9] YI Yang, DING Jia. A novel video salient object extraction method based on visual attention[J]. Signal processing image communication, 2013, 28(1): 45-54. [10] KESHANCHI B, SOURI A, NAVIMIPOUR N J. An improved genetic algorithm for task scheduling in the cloud environments using the priority queues: formal verification, simulation, and statistical testing[J]. Journal of systems and software, 2017, 124: 1-21. [11] ZHANG Junhao, XIA Pinqi. An improved PSO algorithm for parameter identification of nonlinear dynamic hysteretic model[J]. Journal of sound and vibratione, 2017, 389: 153-167. [12] DENG J L. Control problems of unknown system[J]. Proceedings of the bilateral meeting on control systems, 1981: 156-171. [13] 肖冰松,方洋旺. 一种新的超视距空战威胁评估方法[J].系统工程与电子技术, 2009, 31(9): 2163-2166. XIAO Bingsong, FANG Yangwang. New threat assessment method in beyond-the-horizon range air combat[J]. Systems engineering and electronics, 2009, 31(9): 2163-2166. [14] 郭辉,徐浩军,谷向东,等. 基于改进粒子群算法的协同多目标攻击空战决策[J].火力与指挥控制, 2011, 36(6): 49-51. YANG Rong, LI Changjun, GONG Huajun, et al. Air-combat decision-making for cooperative multiple target attack based on improved particle swarm algorithm[J]. Fire control & command control, 2011, 36(6): 49-51. [15] 王俊杰,党耀国,李雪梅,等. 连续型区间灰数排序的应用研究[J].系统工程, 2014, 32(8): 148-152. WANG Junjie,DANG Yaoguo, LI Xuemei, et al. Research on the application of sorting interval grey number of continuous type[J]. Systems engineering, 2014, 32(8): 148-152. [16] 罗德林,王彪,龚华军,等. 基于SAGA的协同多目标攻击决策[J].哈尔滨工业大学学报, 2007, 39(7): 1154-1158. LUO Delin, WANG Biao, GONG Huajun, et al. Air combat decision-making for cooperative multiple target attack based on SAGA[J]. Journal of Harbin Institute of Technology, 2007, 39(7): 1154-1158. 本文引用格式: 宋遐淦, 江驹, 徐海燕. 改进模拟退火遗传算法在协同空战中的应用[J]. 哈尔滨工程大学学报, 2017, 38(11): 1762-1768. SONG Xiagan, JIANG Ju, XU Haiyan. Application of improved simulated annealing genetic algorithm in cooperative air combat[J]. Journal of Harbin Engineering University, 2017, 38(11): 1762-1768. Applicationofimprovedsimulatedannealinggeneticalgorithmincooperativeaircombat SONG Xiagan1, JIANG Ju1, XU Haiyan2 (1.College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China; 2.College of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China) The corresponding evaluation and assignment model is established to solve the problem of weapons target assignment in dynamic uncertain environments. Firstly, the index system of air combat situation assessment is established and the interval analytic hierarchy process and fuzzy optimization are used to obtain the subjective and objective weight of these indexes. Secondly, corresponding effectiveness evaluation mode of multi-objective optimization is constructed with a dynamic environment, and the decision-making problem for cooperative multiple target attack is converted to the optimization problem for missile attack matching. Furthermore, the interval grey number-simulated annealing genetic algorithm is put forward to solve this problem. The proposed ISAGA designs a new selection operation and a special simulated annealing mechanism to enhance the global search ability. Finally, the reasonable attack scheme can be confirmed according to the optimal solution, and simulation results show that the proposed algorithm can be used to evaluate and optimize the weapons target assignment problem in uncertain environments and obtains a solution closer to the optimal solution in ten iterations, which is a consummation to some extent. interval analytic hierarchy process; possibility degree function; interval grey number; simulated annealing; cooperative air combat 10.11990/jheu.201606094 http://www.cnki.net/kcms/detail/23.1390.u.20170427.1544.152.html V249 A 1006-7043(2017)11-1762-07 2016-06-30. 网络出版日期:2017-04-27. 国家自然科学基金项目(71471084,61304223);南京航空航天大学研究生开放基金项目(kfjj20150320,kfjj20150323,kfjj20160318). 宋遐淦(1990-), 男, 硕士研究生; 江驹(1963-), 男, 教授,博士生导师; 徐海燕(1963-),女,教授,博士生导师. 宋遐淦,E-mail:Songxiagan@Foxmail.com.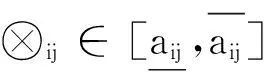


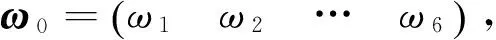
2 空战决策问题数学模型
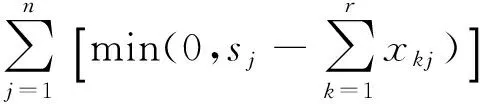
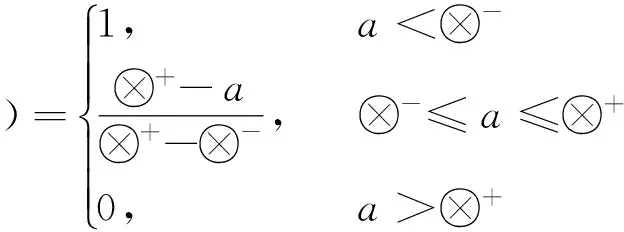
3 基于协同攻击ISAGA的模型求解
4 算法对比性仿真分析




5 结论

