低温液氮冻结食品传热研究
方进林 柳建华,2 梁亚英 周小清
(1上海理工大学能源与动力工程学院 上海 200093;2上海市动力工程多相流动与传热重点实验室 上海 200093)
低温液氮冻结食品传热研究
方进林1柳建华1,2梁亚英1周小清1
(1上海理工大学能源与动力工程学院 上海 200093;2上海市动力工程多相流动与传热重点实验室 上海 200093)
本文采用液氮汽化后的低温氮气与食品接触进行热交换,搭建了低温液氮实验装置,研究了液氮冻结传热过程中热流量和冷却速度的变化规律。在-170~-50℃之间以-20℃为间距设置7个温区进行冻结实验,将马铃薯从初始温度18℃降至冻结点-18℃。采用拟合公式法对采集的数据进行计算,得到换热过程的平均热流量和温度分布;分析热流量变化规律及温度变化率得到最佳氮气温度。结果表明:当氮气温度为-122.87℃时,热流量增长速率达到最大值,继续降低温度,热流量增长幅度减小,此时有部分热量聚于内部,造成冷量浪费;通过对食品中心-3℃时不同界面的温度变化率计算,得到最佳氮气温度为-133.11℃,与前者仅相差6.71%。因此,-128℃左右的氮气温度为最佳温度,既可以保证食品实现快速冻结又可以提高氮气的有效利用率。
冻结食品;冷却速度;冻结点;热流量;拟合公式法
随着人们生活水平不断提高,对食品保鲜越发重视,其中运输储藏尤为重要。近年来,液氮速冻技术逐渐取代化学、生物、气调、非低温保藏等保鲜技术,成为研究热点[1-8]。热流量作为评价冻结质量的主要指标之一,准确获取液氮降温过程中的热流量变化和最佳温度,对食品保鲜、液氮的高效利用和加工工艺具有重大意义。段振华等[9]对比液氮冻结与冰柜冻结的槟榔,发现液氮冻结的食品仍保持了较高的叶绿素;刘宝林等[10]将食品直接放在-196℃的氮气中,研究了冻结过程中潜热和显热的热交换;郭旭峰等[11]采用数值计算对比了黄瓜片在普通鼓风机冷冻、普通流态化速冻及液氮喷淋流态化速冻工况的冻结时间;赖建波等[12]通过对有限长圆柱状食品冻结过程的研究,提出了冻结时间的具体计算方法;曲春民等[13]利用改进焓法进行数值模拟,研究了鲜食玉米冻结过程传热分析及冻结时间。
综上所述,目前研究方向大多集中于液氮冻结方法和冻结时间,而对具体换热过程的研究甚少。本文搭建了低温液氮冷冻实验台,从食品换热的热流量、各界面降温程度等方面着手研究低温氮气与食品的换热过程。
1 实验装置与方法
1.1 实验装置
实验装置如图1所示,主要包括三个部分:采集系统、测温系统和冻结系统。块茎类食品马铃薯因模型制作简单,水分结冰对食品导热影响显著,质地均匀和具有代表性,适合作为研究冻结过程的理想原材料。因此,将马铃薯制作成长度4 cm、直径2 cm的圆柱状,初始温度为18℃,冻结终温[14]-18℃。冻结氮气温度段选为-170~-50℃,以-20℃为间距的7个温区。感温元件采用T型热电偶;采集仪器使用安捷伦采集仪(Agilent34970A);PC上位机软件采用Lab⁃VIEW进行编程,可进行无间断地采集。为了测量食品各处温度,且不引起相邻热电偶串通导致测温相同破坏实验样品,在食品由内到外r=0、r=0.33、r=0.67、r=0.9 cm 布置 4 个测点,同时在距离食品表面0.2 cm处布置一点,测量食品周围氮气温度,以验证食品是否处于设定的氮气温度下冻结。

图1 液氮冻结马铃薯实验装置Fig.1 Liquid nitrogen freezing potato experiment device
1.2 实验方法
液氮冻结马铃薯实验测温过程:首先向杜瓦瓶内充入适量氮气,达到设定值后充氮结束,关闭氮气阀;敞开杜瓦瓶使罐内氮气气化一段时间后,开始测量内部的氮气温度场;打开安捷伦采集仪,同时打开计算机上位机温度采集软件进行温度采集,将布置好测点的杆子缓慢放入罐内,开始采集后观察各通道数据的变化,若温度变化在±0.1℃内,表示温度场稳定;通过测量及计算后确定杜瓦瓶中各温度氮气的位置,将马铃薯缓慢放在某一高度的氮气中降温,并由采集仪和计算机记录马铃薯冻结至-18℃过程中各处的温度变化和冻结时间,完成马铃薯在该氮气温度下的冻结实验。重复上述步骤,改变食品所处位置,获取不同氮气温度下的食品冻结过程中各处温度。当7个温区氮气冻结马铃薯均完成后,关闭Lab⁃VIEW测温系统,马铃薯冻结实验结束。
2 实验数据分析
2.1 热流量理论
氮气与食品接触换热是一个由内到外的变化过程,外部属于对流换热,食品冻结过程中温度随时间而变化,属于非稳态导热。对于食品具体某一界面而言,热交换过程必承接前一界面放出的热量,再将部分热量传给下一个界面,相邻界面间由温差引起的导热量各不相同。计算冻结交界面时,前一个界面已属于冻结面,下一个界面还未结冰且正处于结冰过程,加上冰的生成热对传热的影响,传递的热量变得复杂且存在不确定性。随着温度降低,水分结冰由外向内层层推进,改变了食品成分,使食品在该界面的导热率发生变化,从这个角度看此界面上单位时间热量的传递量也存在不确定性。整体而言,食品内部换热量与氮气温度和食品表面温差有很大联系,食品内部一定界面上单位时间所传递的热量(热流量)随着温差的增加而增大。当温差过大时,食品内部热流量增加程度有限,无法将热量完全传出使部分聚集在内部,严重时发生冻伤。因此,理想温差条件下热流量能恰好将热量传出,提高内部降温速率,快速通过最大结晶区,生成细小而均匀的冰晶,同时又无残余热量积累,达到高效换热。综上所述,对某界面热流量无法具体计算,本文通过计算整个食品的冻结换热量,得到食品降温的平均热流量:

确定各温差条件下的食品平均热流量Φm后,分析其随氮气温度降低的增长幅度,当Φm增长幅度达到最大值时对应最佳的冻结食品温差tN2:

对于传热量的计算,由于食品在冻结过程中各处的温度随着时间而降低,将冻结非稳态传热过程作简化处理,假设:1)一维导热,冻结食品纵向无传热,温度仅在x方向上发生变化;2)没有内热源;3)食品初始温度t1已知;4)冻结食品的冷介质温度t5恒定;5)食品各向同性,几何形状是简单规则的。简化后,得到导热微分方程及定解条件:

引入过余温度:

食品冻结过程导热进行一定深度后,初始条件对食品温度分布的影响基本消失,主要取决于物性和周围冷介质的影响。利用初等函数求解一段时间间隔内的传热量,解析表达式可以简化为:

式中:Q0为从初始时刻到食品与周围冷介质处于热平衡整个过程中所传递的热量,即该非稳态导热过程所能传递的最大热量,Q0=ρcV(t1-t5),J;μ1为第一特征值,对应几何形状食品的超越方程的根,与Bi有关;F0为傅里叶数,F0=aτ/δ2;J0(x) 为零阶贝塞尔函数;J1(x)为第一类一阶贝塞尔函数,J1(x)=-J0(x)。
几何形状食品的正常阶段导热量为:

利用上述公式计算时,涉及复杂的函数和插图。图线法由于受图线分辨率的限制,易使数据有较大误差,因此本文采用拟合公式法[15]:

式中:A、B均为系数,a、b、c、d 均为常量,查文献可知。
确定相关参数后通过上述计算公式,即可求解平均热流量。
2.2 冻结温差与温度变化率
不同温度氮气冻结相同食品降温至同一温度时,食品内部结冰率相同[16],以食品内部各成分所占比例计算得到的该温度下食品导热率相同,根据傅里叶定律可知,此时该界面的热流量与当地垂直于截面上的温度变化率成正比。研究各温度氮气下食品某一界面的微元温度变化率的前提是确定分析温度变化的具体时间。影响食品冻结时间的关键在于食品中心通过最大结晶区的快慢程度,冰晶的生成尺寸及分布决定了食品的冻结质量。以食品中心通过-5~-1℃温区的中间点-3℃为研究点,分析此时某界面微元的温度变化率随温差增大的增长幅度,获得冻结食品的最佳氮气温度。计算如下:

式中:tN2n为食品第n个界面的最佳氮气温度,℃;为食品第n个界面温度变化率。
3 结果分析
3.1 食品平均热流量变化规律
表1为不同氮气温度下食品平均热流量计算。
图2所示为马铃薯在各氮气中冻结的平均热流量,平均热流量随氮气温度的降低而增大。将各热流量对氮气温度进行求导,得到食品平均热流量导函数如图3所示,当tN2=-122.87℃时,热流量导函数达到最小值,平均热流量的增长速度最快,dΦm/dτN2= -48.92×10-3。 随着温差继续增大,氮气的温度继续降低,热流量导函数值逐渐增大,平均热流量的增加幅度逐渐减小。因为当t5>tN2时,食品内部热量开始无法及时传出,开始有部分聚集,即开始有部分冷量剩余,未及时完全利用。因此,从增大温差增强换热量,加快食品冻结速率,缩短食品冻结时间来看,冻结马铃薯的最佳氮气温度为-122.87℃,此时内部生成细小、均匀的冰晶。
3.2 食品不同界面的温度变化规律
研究食品中心通过最大结晶区-3℃,得到不同界面的温度变化率随温差增大的增长规律,获得温度变化率变化最大时对应的氮气温度,如表2所示。
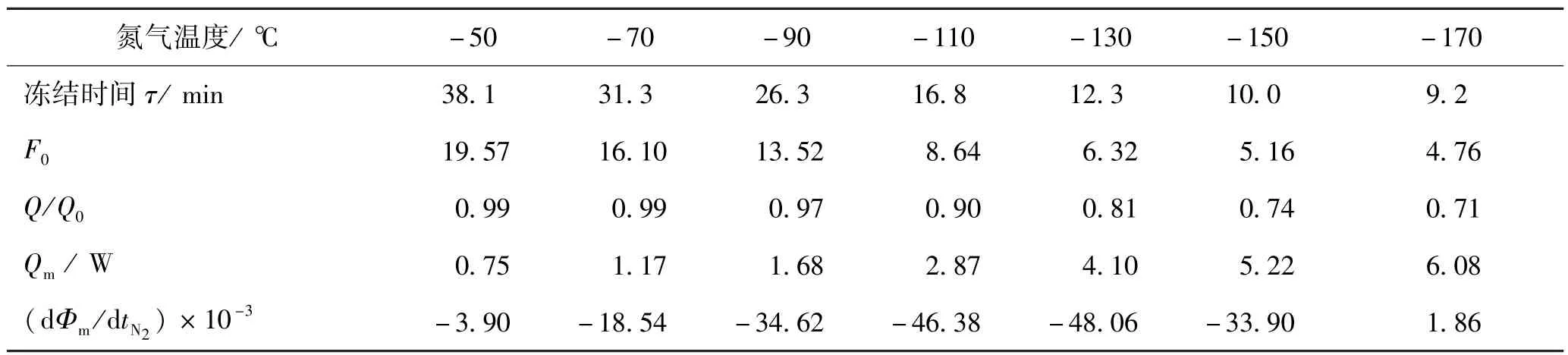
表1 不同氮气温度下食品的平均热流量计算值Tab.1 The calculation of food average heat flux at different nitrogen temperatures
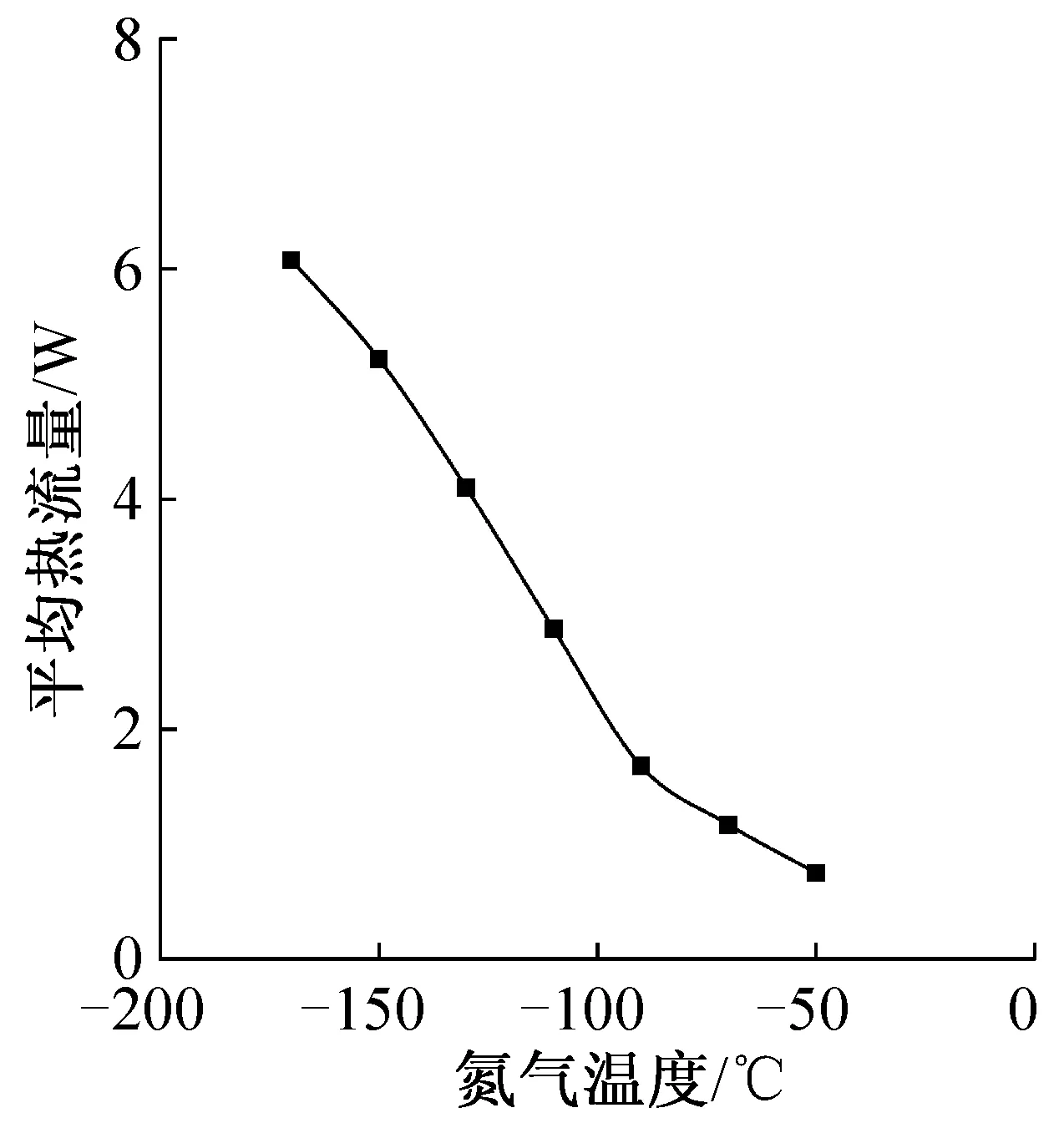
图2 不同氮气温度中食品平均热流量Fig.2 Food average heat flux at different nitrogen temperatures

图3 不同氮气温度中食品平均热流量导函数Fig.3 The heat conduction function of food average heat flux at different nitrogen temperatures

表2 不同氮气温度下食品中心降至-3℃时各界面的温度分布Tab.2 Various interfaces temperature distribution at different nitrogen temperatures when food center dropped to -3 ℃
由于r=0 cm和r=0.9 cm处于温度分布的两端,温度变化率不确定,因此选取r=0.33 cm和r=0.67 cm两个界面,在各氮气温度下的温度变化率如表3所示。
如图4所示,随着氮气温度的增加,温度变化率逐渐增大。如图5所示,tN21=-122.22℃时的温度变化率导函数值最大,温度变化率的增长幅度达到最大。氮气温度继续降低,同样有热量逐渐积聚在此,降低了冷量利用率。
图6与图7分别为r=0.67 cm界面在不同温度氮气下冻结时的温度变化率及对氮气温度求导的导函数,tN22=-140℃时的导函数值最大,温度变化率增长速度最快,冷量利用率最高。结合r=0.33 cm界面的温度变化率最大时刻的温度值求得马铃薯冻结的最佳氮气温度值tN2=-131.11℃,与利用食品平均热流量求得的氮气温度相比,二者相差不大,偏差仅为6.71%。造成偏差的主要原因是选取的食品界面较少,不能准确的反映食品内部的温度分布状况。
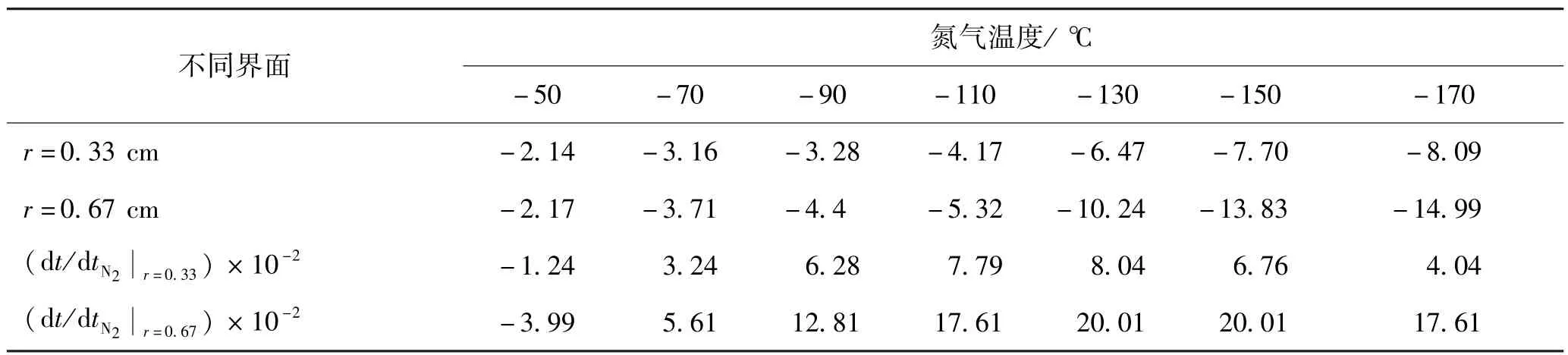
表3 不同氮气温度下食品不同界面的温度变化率Tab.3 The temperature change rate of food different interfaces at different temperature
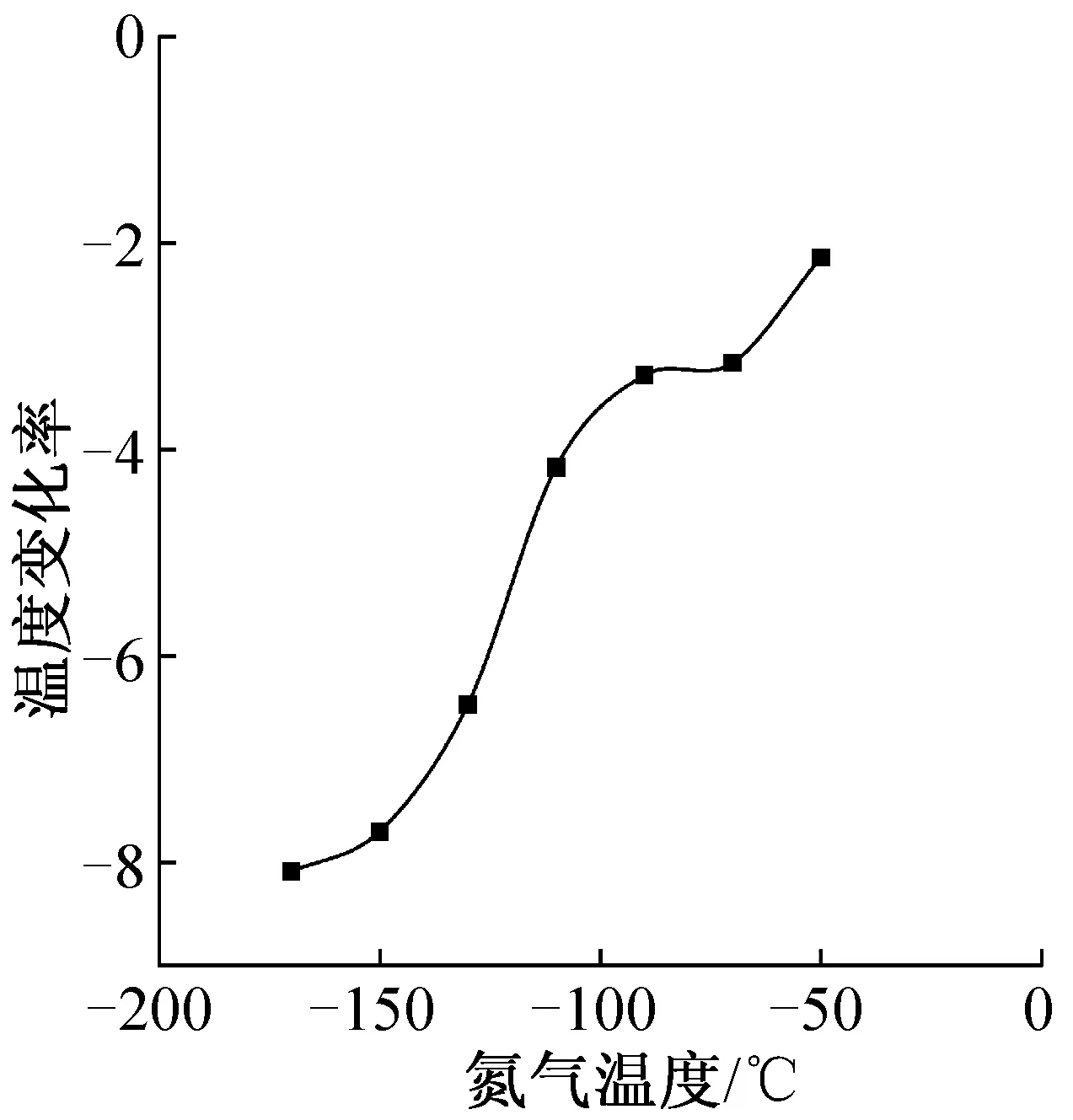
图4 r=0.33 cm界面的温度变化率Fig.4 Temperature change rate of r=0.33 cm interface

图5 r=0.33 cm界面的温度变化率导函数Fig.5 Temperature change rate conduction function of of r=0.33 cm interface
4 结论
本文搭建了低温液氮冻结实验台,将有限长圆柱状马铃薯在-170~-50℃的液氮环境中分成7个温区,从18℃冻结至-18℃,分别测得冻结时间和各界面的温度。整理数据并分析得出以下结论:

图6 r=0.67 cm界面的温度变化率Fig.6 Temperature change rate of r=0.67 cm interface
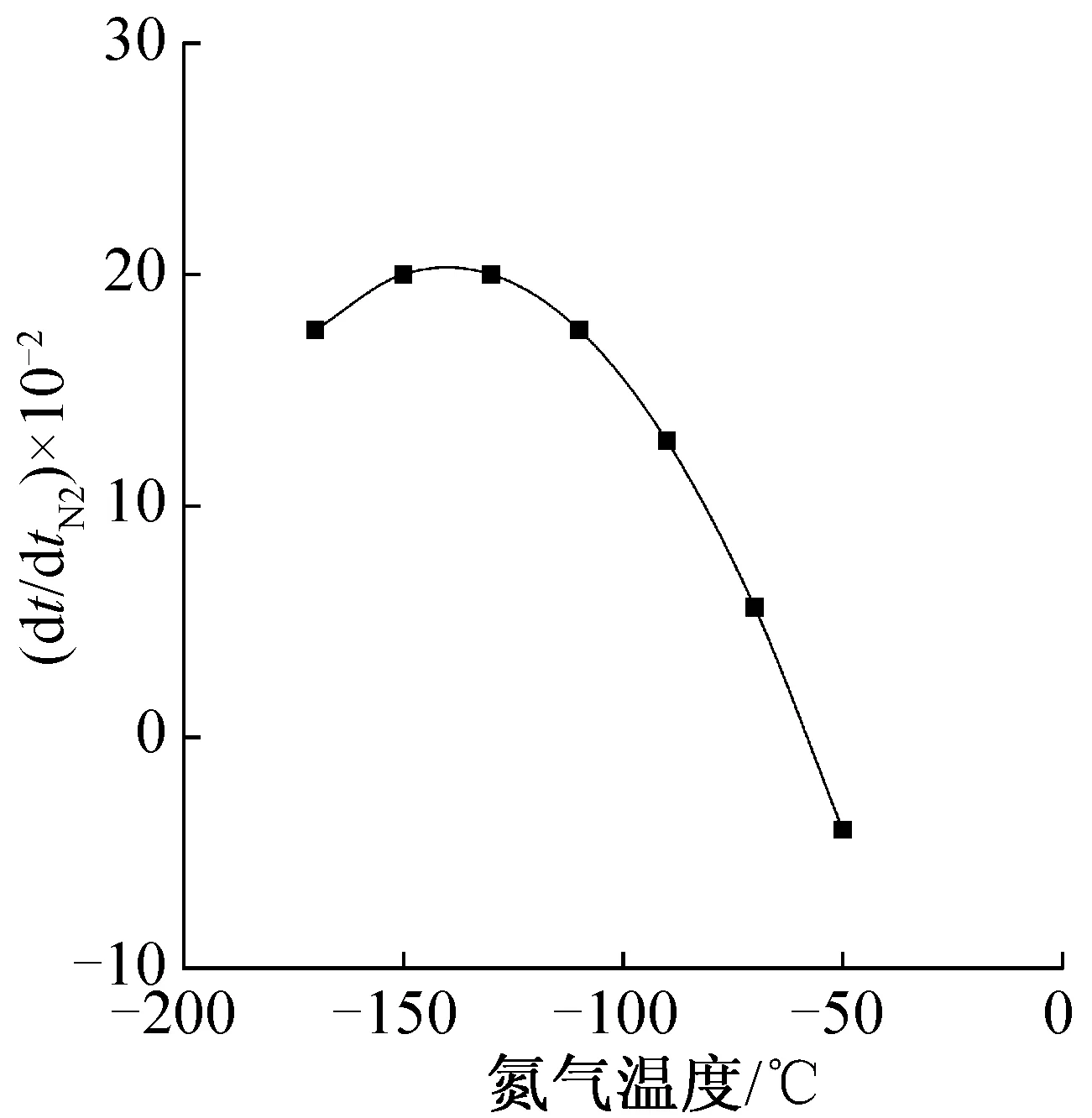
图7 r=0.67 cm界面的温度变化率导函数Fig.7 Temperature change rate conduction function of r =0.67 cm interface
1)在-170~-50℃的液氮环境中冻结马铃薯过程属于非稳态导热,具体某一界面的热流量由于受相变潜热及马铃薯成分改变而无法准确计算,通过计算食品冻结过程中的换热量求得平均热流量,得出平均热流量随氮气温度的降低而增大。当马铃薯置于-122.87℃氮气中时,热流量增长率最大,此时内部无热量剩余,换热性能最好,食品冻结时间达到经济最小值。
2)利用-170~-50℃低温氮气冻结食品,分析r=0.33 cm 和r=0.67 cm 两界面的温度变化率随氮气的增长幅度,得知在-133.11℃的氮气温度下冻结食品,冷量利用率最高。食品的温变速率增长有快慢之分,在加强食品与冷介质的换热方式上,并不是温差越大越好。
符号说明
Q——食品冻结至-18℃的换热量,J
x——x方向上的单位距离,m
τ——食品冻结至-18℃的时间,min
t5——冻结食品的氮气温度,℃
Φm——平均热流量,J/s
a——食品的热扩散率,m2/s
δ——食品的一半厚度或者半径,m
λ——食品的导热系数,W/(m·K)
α——食品周围冷介质的表面传热系数,W/(m2·K)
ρ——食品的密度,kg/m3
c——食品的比热容,J/(kg·℃)
V——食品的体积,m3
本文受上海市教育委员会重点学科项目(J50502),上海市科委建设项目(13DZ2260900)和上海市部分院校能力建设专项计划项目(16060502600)资助。 (The project was suppor⁃ted by the Key Program of Shanghai Municipal Education Commis⁃sion (No.J50502),Construction Project of Shanghai Science and Technology Committee (No.13DZ2260900),and Capacity Build⁃ing Plan for Some Nonmilitary University and Colleges of Shanghai Scientific Committee(No.16060502600).)
[1]郭旭峰,陶乐仁,华泽钊,等.液氮速冻装置中液氮耗量与冷冻能力的分析[J].低温与特气,2002,20(5):8⁃11.(GUO Xufeng,TAO Leren,HUA Zezhao,et al.Anal⁃ysis of LN2(Liquid Nitrogen) consumption and freezing ca⁃pacity on LN2freezer[J].Low Temperature and Special Gases,2002,20(5):8⁃11.)
[2]EINARSSON H,LAUZON H L.Biopreservation of brined shrimp (pandalus borealis) by bacteriocins from lactic acid bacteria[J].Applied and Environmental Microbiology,1995,61(2):669⁃676.
[3]何耀辉,卢敏仪,刘康,等.气调包装技术用于草虾保鲜的研究[J].食品与发酵工业,2001,27(2):26⁃29.(HE Yaohui,LU Minyi,LIU Kang,et al.Modified atmosphere packaging for penaeus monodon[J].Food and Fermenta⁃tion Industries,2001,27(2):26⁃29.)
[4]RUTHERFORD T J,MARSHALL D L,ANDREWS L S,et al.Combined effect of packaging atmosphere and storage temperature on growth of Listeria monocytogenes on ready⁃to⁃eat shrimp[J].Food Microbiology,2007,24(7/8):703⁃710.
[5]刘丽珍,韩云峰.论中小型渔船制冷保鲜发展动态与趋势[J].海洋水产研究,2007,28(2):113⁃117.(LIU Liz⁃hen,HAN Yunfeng.Discussion on the development and tendency in small⁃and medium⁃sized fishing vessel refrige⁃ration[J].Marine Fisheries Research,2007,28(2):113⁃117.)
[6]樊建,赵天瑞,曹建新,等.草莓液氮速冻工艺研究[J].制冷学报,2008,29(2):60⁃62.(FAN Jian,ZHAO Tian⁃rui,CAO Jianxin,et al.Study on strawberry freezing tech⁃nique by liquid nitrogen quick freezing[J].Journal of Re⁃frigeration,2008,29(2):60⁃62.
[7]刘宝林,华泽钊,任禾盛.冻结食品的玻璃化保存[J].制冷 学 报,1996,17 (1):26⁃31.(LIU Baolin,HUA Zezhao,REN Hesheng.Vitrification preservation of frozen foods[J].Journal of Refrigeration,1996,17(1):26⁃31.)[8]GRIGULL U,SANDNER H.Heat conduction[M].Wash⁃ington: Hemisphere Publishing Corporation,1984.
[9] 段振华,张敏,张剑锋,等.槟榔速冻工艺研究[J].冷饮与速冻食品工业,2002,8(3):10⁃13.(DUAN Zhenhua,ZHANG Min,ZHANG Jianfeng,et al.Study on technology of quick frozen areca fruits[J].Beverage & Fast Frozen Food Industry,2002,8(3):10⁃13.)
[10]刘宝林,郭勇建,屠建祥,等.一种新型的流态化速冻装置[J].制冷学报,2000,21(4):49⁃52.(LIU Baolin,GUO Yongjian,TU Jianxiang,et al.A new type of fluidized freezing system [J].Journal of Refrigeration,2000,21(4):49⁃52.)
[11]郭旭峰,陶乐仁.液氮喷淋流化床速冻系统及冷冻性能研究[J].工程热物理学报,2003,24(3):475⁃477.(GUO Xufeng,TAO Leren.Investigation on freezing char⁃acteristic of LN2⁃spraying fluidized cooling system [ J].Journal of Engineering Thermophysics,2003,24(3):475⁃477.)
[12]赖建波,臧润清,车晶.有限长圆柱状食品冻结时间的计算方法及实验验证[J].制冷,2003,22(3):19⁃23.(LAI Jianbo,ZANG Runqing,CHE Jing.Calculating method and experimental verification on freezing time of finite cycli⁃cal foodstuff[J].Refrigeration,2003,22(3):19⁃23.)
[13]曲春民,孙勇,陈忠海,等.鲜食玉米冻结过程传热分析及冻结时间的研究[J].制冷学报,2006,27(6):34⁃38.(QU Chunming,SUN Yong,CHEN Zhonghai,et al.Research on heat transfer process of the quick freezing of the fresh unripe maize and freezing time[J].Journal of Re⁃frigeration,2006,27(6):34⁃38.)
[14]包建强.食品低温保藏学[M].北京:中国轻业出版社,2011.(BAO Jianqiang.Food preservation under low tem⁃perature[M].Beijing: China Light Industry Press,2011.)
[15]关志强,李敏.食品冷冻冷藏原理与技术[M].北京:化学工业出版社,2010.(GUAN Zhiqiang,LI Min.Principle and technology of food freezing and refrigeration[M].Bei⁃jing: Chemical Industry Press,2010.)
[16]Yong H C.Effects of temperature and composition on the thermal conductivity and thermal diffusivity of some food components[J].Korean Journal of Food Science & Tech⁃nology,1986,18(5):83⁃92.
Heat Transfer Research on Food Frozen by Cryogenic Liquid Nitrogen
Fang Jinlin1Liu Jianhua1,2Liang Yaying1Zhou Xiaoqing1
(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai,200093,China;2.Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering,Shanghai,200093,China)
To study the heat⁃flux change and cooling rate in the freezing and heat⁃transfer process of liquid nitrogen,a low⁃temperature liquid⁃nitrogen experimental device was made.It was based on the idea of the direct contact heat exchange with the food after the liquid nitrogen vaporized.The experiment was conducted at seven temperature regions ranging from -50℃ to -170℃ with -20℃ interval.A potato was frozen from the initial temperature 18℃ to the freezing point-18℃.The average heat flux and the temperature distribution of the heat⁃transfer process were calculated using a curve⁃fitting formula.The heat⁃flux change and temperature change rate were analyzed to obtain the most appropriate nitrogen temperature.The results show that when the nitrogen temperature is -122.87 ℃,the heat⁃flux growth rate reaches the maximum.As the temperature continues to reduce,the heat⁃flux growth rate decreases;at this point,part of the heat gathered internally from the food results in wasted energy.The temperature change rate for different interfaces was calculated when the food⁃center temperature was -3 ℃,and the optimum nitrogen temperature was found to be -133.11 ℃.This was only 6.71%dif⁃ferent from the previous result.Thus,the optimum nitrogen⁃freezing temperature is about -128 ℃,which can ensure the rapid freezing of the food and improve the effective utilization of the nitrogen.
frozen food;cooling rate;freezing point;heat flow;fitting formula method
Fang Jinlin,male,master degree candidate,School of Energy and Power Engineering,University of Shanghai For Science and Tech⁃nology,+ 86 18721992864,E⁃mail:584982745@ qq.com.Re⁃search fields: refrigeration and cryogenic technology.
TB61+1;TS205.7;TK124
A
0253-4339(2017)06-0099-07
10.3969 /j.issn.0253 - 4339.2017.06.099
2016年11月24日
方进林,男,硕士研究生,上海理工大学能源与动力工程学院,18721992864,E⁃mail:584982745@ qq.com。 研究方向:制冷及低温工程。

