参比温度曲线法的改进与实验研究

王赞社 杨利生 胡显威 罗昔联 顾兆林

（西安交通大学人居环境与建筑工程学院建筑技术与建成环境研究所 西安 710049）

参比温度曲线法的改进与实验研究

王赞社 杨利生 胡显威 罗昔联 顾兆林

（西安交通大学人居环境与建筑工程学院建筑技术与建成环境研究所 西安 710049）

相变蓄热材料应用广泛，其热物性的测量至关重要。本文基于参比温度曲线法的基本思想，从相变蓄热材料的理论步冷曲线特征和实际测量过程出发，针对相变阶段中能量平衡方程的显热因素和相变结束阶段降温过程的温差因素进行分析和改进，得到了改进后的计算方程。并以十二水磷酸氢二钠、月桂酸和硬脂酸三种相变材料为例进行相变材料步冷曲线的实验研究，结合改进后的计算方程进行相变潜热值的计算。结果表明：改进后的方程对潜热的计算值与DSC测量值相比更接近，误差控制在10%以内。参比温度曲线法的改进对于相变蓄热材料的快速开发和调制具有一定的实践指导意义。

参比温度曲线法；相变；潜热

相变蓄热材料（PCM）具有非常高的应用价值。由于单位体积的蓄能密度大，蓄热温度稳定等优点，在热量存储，余热回收，太阳能热利用，建筑围护结构蓄能，能量调峰等领域广泛应用［1］，国内外对相变蓄热材料及其应用的研究广泛而深入［2－3］。然而，由于能量来源不同，能源品位不同，用途不一，对于相变蓄热材料的经济性、种类、性能，尤其是热物性的要求多种多样。因此，对相变材料热物性的测量和方法是其应用的前提和关键。

相变材料热物性传统测量方法有：常规卡计法、差热分析法（DTA）和差示扫描量热法（DSC）等。常规卡计法不能同时测定多种相变材料的热物性参数而且相变过程不便观察；DTA法和DSC法在测量时所用材料都在mg级，不能体现实际应用中大块材料的热物性和相变现象［4］。 1997—1999 年，张寅平等［5－6］研究了一种能够测定多组相变材料凝固点、比热、潜热、导热系数和热扩散系数的新方法——参比温度曲线法（T⁃history），该方法所用相变材料的量大，更接近于实际应用过程，相变过程也易观察，是一种简单有效的测量方法。 此后，H．Hong等［7－9］对参比温度曲线法进行改进，加入了相变阶段的显热部分，选取步冷曲线的拐点作为相变结束点，给出了改进后的比热和潜热值的计算方程，提高了应用可行性。 E．D．Krawwaritis等［10－11］引入热迟滞对不同相变材料进行了测试，提高了结果的准确度。L．Moreno⁃Alvarez等［12－13］在考虑温度变化快慢的基础上提出了参比温度曲线法的微积分形式，分别对粒状相变复合材料进行了实验研究，并对J．M．Marin等［14］实验材料进行了理论分析，得出热物性尤其是比热和潜热值与相转变的理论值具有一致性。J．M．Marin等［14］提出了参比温度曲线法的焓⁃温曲线法代替步冷曲线，并对石蜡类相变蓄热材料进行实验，实验结果与DSC测试结果相差10% ～15%。A．Lazaro等［15］利用焓值法对热物性已知的材料进行实验验证，结果准确性较高。E．Guenther等［16］比较了DSC和参比温度曲线焓值法，显示两种方法的结果具有较好的一致性。M．A．Rady等［17］比较了DSC法和参比温度曲线焓值法对胶囊化相变蓄热材料的处理结果，两者具有较好的一致性。李瑶等［18］等分别以高次多项式和三次样条插值法拟合实验数据用以确定相变潜热值，结论是采用三次样条插值拟合法计算PCM的相变潜热最稳定且接近理论值，而以一阶导数最高点为相变起始点计算无过冷度相变材料的相变潜热结果更精确。

相变材料是所属系统的关键要素，相变材料的热物性对系统性能计算和评估至关重要。虽然参比温度曲线法提供了相变材料简单易行的热物性测量方法，但该模型是建立在时间⁃温度的标准理想化曲线，实际测量得到的曲线有一定的偏差，对于相变材料管外换热效率，相变始点和终点的选取也有一定的争议［19］。

本文在已有研究的基础上，进一步改进参比温度曲线法中比热和潜热值的计算方程，并进行实验验证。

1 参比温度曲线法的基本思想

装有相变材料和参比材料水的试管组在恒温水浴中加热到温度T0（T0＞Tm，Tm是相变材料的相变温度），快速放置在温度为Ta的空气环境中自然冷却，测量得到该材料的步冷曲线图。对于有过冷现象的相变材料，还要满足（Tm－Ta） ＞（Tm－Ts）（Ts为相变开始的温度）。其中ΔTm＝Tm－Ts称为过冷度。图1所示为参比温度曲线法的原理。

图1 参比温度曲线法原理Fig．1 Principle of the T⁃history

参比温度曲线法的关键条件是满足毕渥数Bi＜0.1（Bi＝hR/（2k），R为试管半径，m；k为相变材料导热系数，W/（m·K）；h为试管外空气的自然对流换热系数，W/（m2·K）），此时可认为试管内的相变蓄热材料的温度分布均匀并且其传热分析可用集总热容法［5］。

由图1（a）的能量平衡得到如下方程：

式中：mt为试管质量，kg；cp，t为试管比热容，J/（kg·K）；mp为相变材料质量，kg；cp，l为相变材料的液态比热容，J/（kg·K）；Ac为试管对流换热面积，m2；为相变潜热值，kJ/kg；为相变材料的固态比热，J/（kg·K）；为基准温度，K。

同样，对于装水的试管（水温、体积与PCM试样相同，实验过程相同），由图1（c）的能量平衡可以得到如下方程：

式中：mw为水的质量，kg；cp，w为水的比热，Ta）dt，K·s。

由式（1）～式（5）可以得到相变材料的比热容和相变潜热：

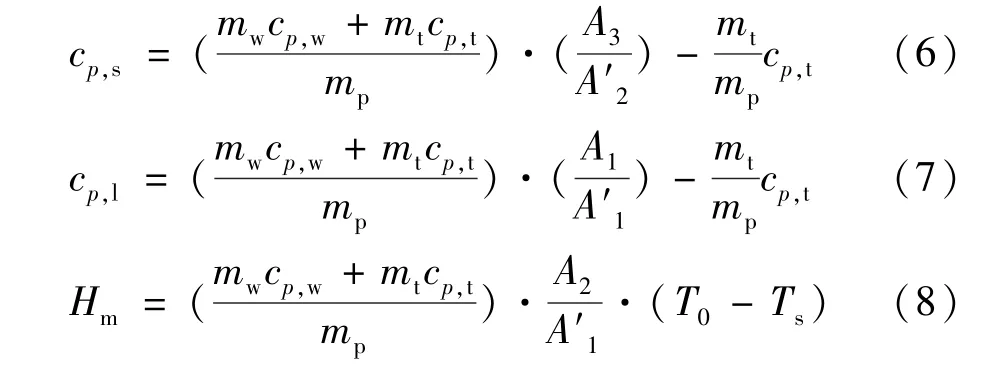
对于无过冷相变材料，步冷曲线如图1（b）所示，相变时间段为t1－t2。无过冷相变材料的液态比热和固态比热的表达式如式（6）和式（7）所示，其相变潜热方程为：

2 参比温度曲线法的改进

综上所述，已有学者对参比温度曲线法进行了深入研究并提出改进，步冷曲线相变拐点的选取［7－9］、热迟滞法［10－11］、微积分法［12－13］、相转变理论分析法［14］、多项式和样条插值法［18］等虽然在不同程度提高了热物性获取的准确性，但针对形式多样的相变材料，要完成不同性能参数要求的相变材料测试，这些改进方法相对复杂。本文从PCM的理论步冷曲线特征和实际测量过程出发，在相变阶段能量平衡方程中的显热因素方面入手进行分析和改进。

式（2）是相变阶段的能量平衡方程，在参比温度曲线法中，认为相变开始和相变结束温度Ts相同，如图1（a）所示，此时，相变阶段不计材料显热温升。而在实际过程中，尤其是有过冷现象的相变材料，相变阶段显热温升是由潜热释放所引起的。H．Hong等［9］认为相变起始温度Ts和相变终了温度T2并不相同，如图2所示，并针对相变阶段显热温升效应在式（2）能量平衡方程中增加了显热部分热量，如式（10）所示。

图2 考虑显热温升效果的参比温度曲线Fig．2 T⁃history with sensible heat effect

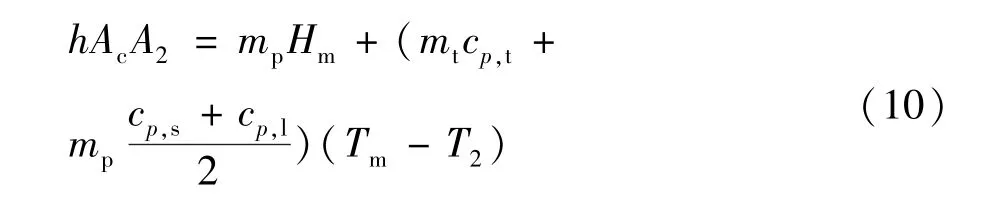
但式（10）中将温差Tm－T2作为相变阶段显热温升效应的驱动来源，不能准确反映相变材料的显热温升机理，原因在于从相变材料晶体熔化的热力学条件而言，Tm是理论凝固温度，而过冷度Tm－Ts是过冷晶体结晶的驱动力［1］，这个阶段的温差Tm－Ts是促成过冷晶体结晶的必要条件，即相变潜热发生的必要条件，Tm－Ts不应该成为显热温升的驱动来源。从相变阶段的能量平衡方程而言，潜热释放与试管外表面自然对流换热量相当。因此对显热温升效应真正起作用的温差应该是相变起始阶段温度Ts和相变终了阶段温度T2之差。改进式（10）可得：

对于无过冷现象的相变材料，Tm＝Ts。因此，选取Ts－T2作为相变阶段显热温升的温差既适用于有过冷现象的相变材料，也适用于无过冷现象的相变材料。

对相变完成后自然冷却阶段的式（3）进行改进，此时温度起点是T2，即将式（3）中的Ts改为T2，可明确表达相变终了后的自然降温过程：

因此，基于改进的参比温度曲线法，相变材料的能量平衡计算方程为式（1）、式（11）和式（12）；参比材料水的能量平衡计算方程是式（4）和式（5）。

由以上方程可以得到改进后的相变材料比热和焓值计算方程为：

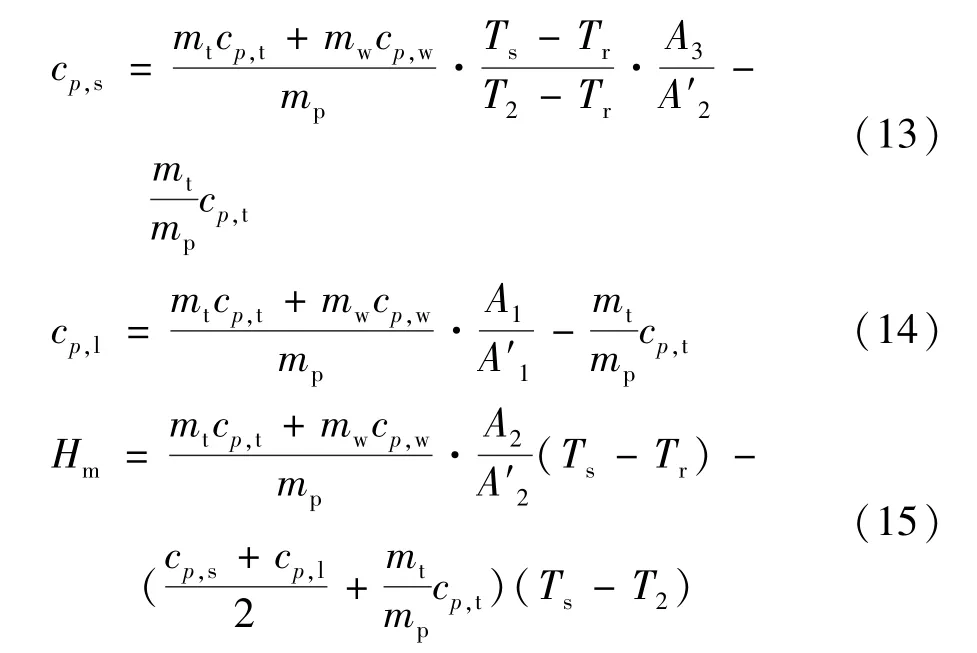
3 实验验证

为了验证改进的参比温度曲线法方程组，对十二水磷酸氢二钠、月桂酸和硬脂酸进行实验研究［20］。将三种相变材料在70℃的恒温水浴中完全熔化后快速放至10℃的恒温箱中自然冷却，2 s记录一次温度数据，得到材料的步冷曲线，如图3和图4所示。

根据测量数据，利用改进前后的参比温度曲线法方程组进行计算，得到各自的相变潜热值，并与文献［21－22］中通过DSC测试方法得到的潜热值进行比较，如表1所示。

图3 Na2HPO4·12H2O的步冷曲线Fig．3 Step curve of Na2HPO4·12H2O

图4 月桂酸和硬脂酸的步冷曲线Fig．4 Step curve of lauric acid and stearic acid

表1 改进前后比热容和潜热值比较Tab．1 Control equations of heat and mass transfer in the membrane heat exchanger

表1中，改进前的潜热计算方程为式（8）和式（9），改进后的潜热计算方程为式（15）。在实验中，每种相变材料进行三次实验，改进前后的潜热计算值均按照三次实验结果计算平均值。在计算过程中，理论相变温度Tm，相变起始温度Ts直接在步冷曲线上选取，由于相变终了温度T2的确定一直存在较大难度和争议［19］，本文采用 H．Hong 等［9］的曲线拐点法来确定，具体做法是将相变终了阶段至自然冷却阶段的数据进行拟合，获取一阶拐点处位置，对应位置上的温度作为相变终了温度T2。从表1中可以看出，改进前的计算结果与DSC的测试值相差较大，而改进后计算的潜热值更加接近DSC方法的测试值，误差更小。因此，改进后的参比温度曲线法方程组更适合于在实际应用中对相变材料进行调制和测试分析。

4 结论

本文基于参比温度曲线法的基本思想，以相变材料的晶体熔化热力学条件、理论步冷曲线特征和实际测量过程为依据，分析和改进了能量平衡方程中的显热因素，在相变阶段增加了以相变起始温度和终了温度之差作为显热温升驱动的影响因素；改进了相变完成后降温冷却阶段的起始温度，构成了改进后的计算方程组。并以十二水磷酸氢二钠、月桂酸和硬脂酸三种相变材料为例进行实验，根据改进的计算方程和实验结果进行验证。结果表明，改进后的参比温度曲线法方程组更接近DSC方法的测试值，误差可以控制在10%以内。改进后的方程组对于相变蓄热材料的开发、调制和测试具有一定的实践指导意义。

［1］张仁元．相变材料与相变储能技术［M］．北京：科学出版社，2009．（ZHANG Renyuan．Phase change material and phase change energy storage ［M］．Beijing：Science Press，2009．）

［2］徐治国，赵长颖，纪育楠，等．中低温相变蓄热的研究进展［J］．储能科学与技术，2014，3（3）： 179⁃190．（XU Zhiguo，ZHAO Changying，JI Yunan，et al．State⁃of⁃theart of phase⁃change thermal storage at middle⁃low temperature［J］．Energy Storage Science and Technology，2014，3（3）：179⁃190．）

［3］TAY N H S，LIU M，BELUSKO M，et al．Review on transportable phase change material in thermal energy stor⁃age systems［J］．Renewable and Sustainable Energy Re⁃views，2017，75： 264⁃277．

［4］李翠敏，赵加宁．低温相变癸酸储热性能改良实验研究［J］．太阳能学报，2011，32（12）：1833⁃1838．（LI Cuimin，ZHAO Jianing．Experiment study on thermal stor⁃age performance improvement of capricacid ［J］．Acta En⁃ergiae Solaris Sinica，2011，32（12）： 1833⁃1838．）

［5］张寅平，郑迎松，葛新石．多组相变材料多个热物性的同时测定性［J］．科学通报，1997，42（14）： 1559⁃1562．（ZHANG Yinping，ZHENG Yingsong，GE Xinshi．Simulta⁃neous determination of multiple thermophysical properties of multiple sets of phase change materials［ J］．Chinese Sci⁃ence Bulletin，1997，42（14）： 1559⁃1562．）

［6］ZHANG Yinping，JIANG Yi．A simple method，the T⁃his⁃tory method，of determining the heat of fusion，specific heat and thermal conductivity of phase⁃change materials［ J］．Measurement Science and Technology，1999，10（3）： 201⁃205．

［7］HONG H，PARK H C，CHOI J H，et al．Improvement of the T⁃history method to measure heat of fusion for phase change materials［ J］．International Journal of Air⁃condi⁃tioning and Refrigeration，2003，11（1）： 32⁃39．

［8］PECK J H，KIM J J，KANG C，et al．A study of accurate latent heat measurement for a PCM with a low melting tem⁃perature using T⁃history method［J］．International Journal of Refrigeration，2006，29 （7）： 225⁃1232．

［9］HONG H，KIM S K，KIM Y S．Accuracy improvement of T⁃history method for measuring heat of fusion of various ma⁃terials［J］．International Journal of Refrigeration，2004，27（4）： 360⁃366．

［10］KRAVVARITIS E D，ANTONOPOULOS K A，TZIVANI⁃DIS C．Improvements to the measurement of the thermal properties of phase change materials［J］．Measurement Sci⁃ence and Technology，2010，21 （4）：1⁃9．

［11］KRAVVARITIS E D，ANTONOPOULOS K A，TZIVANI⁃DIS C．Experimental determination of the effective thermal capacity function and other thermal properties for various phase change materials using the thermal delay method［J］．Applied Energy，2011，88 （12）： 4459⁃4469．

［12］MORENO⁃ALVAREZ L，HERRERA J N，MENESES⁃FA⁃BIAN C．A differential formulation of the T⁃History calori⁃metric method［J］．Measurement Science and Technology，2010，21 （12）：1⁃4．

［13］RADY M．Granular phase change materials for thermal en⁃ergy storage： Experiments and numerical simulations［J］．Applied Thermal Engineering，2009，29 （14/15）： 3149⁃3159．

［14］MARIN J M，ZALBA B，CABEZA L F，et al．Determina⁃tion of enthalpy⁃temperature curves of phase change materi⁃als with the temperature⁃history method： improvement to temperature dependent properties［ J］．Measurement Sci⁃ence and Technology，2003，14 （2）： 184⁃189．

［15］LAZARO A，GUENTHER E，MEHLING H，et al．Verifi⁃cation of a T⁃history installation to measure enthalpy versus temperature curves of phase change materials［J］．Measure⁃ment Science and Technology，2006，17 （8）： 2168⁃2174．

［16］GUENTHER E，HIEBLER S，MEHLING H，et al．En⁃thalpy of phase change materials as a function of tempera⁃ture：required accuracy and suitable measurement methods［J］．International Journal of Thermophysics，2009，30（4）： 1257⁃1269．

［17］RADY M A，ARQUIS E，BOT C L．Characterization of granular phase changing composites for thermal energy stor⁃age using the T⁃history method［J］．International Journal of Energy Research，2010，34 （4）： 333⁃344．

［18］李瑶，钱静，吴丽彬．基于T⁃history曲线计算材料相变潜热方法的改进［J］．包装工程，2014（23）： 17⁃22．（LI Yao，QIAN Jing，WU Libin．Improvement of calculation method for material phase change latent heat based on T⁃history curve［J］．Packaging Engineering，2014（23）： 17⁃22．）

［19］BADENHORST H，CABEZA L F．Critical analysis of the T⁃history method： A fundamental approach［J］．Thermo⁃chimica Acta，2017，650： 95⁃105．［20］胡显威．太阳能相变蓄热材料实验研究及毛细管网辐射供暖性能评估［D］．西安：西安交通大学，2013．（HU Xianwei．Experiment research on solar phase change heat storage materials and performance evaluation of solar phase change heat storage capillary network radiant heating system［D］．Xi′an： Xi′an Jiaotong University，2013．）

［21］张林．脂肪酸混合物的配制及其定形相变墙体的实验研究［D］．北京：北京建筑工程学院，2010．（ZHANG Lin．Preparation of fatty acid and experimental study on the shape⁃stabilized phase change material wall［D］．Beijing：Beijing University of Civil Engineering and Architecture，2010．）

［22］SHARMA A，TYAGI V V，CHEN C R，et al．Review on thermal energy storage with phase change materials and ap⁃plications［J］．Renewable ＆ Sustainable Energy Reviews，2009，13 （2）： 318⁃345．

Improvement and Experimental Study of the T⁃history Method

Wang Zanshe Yang Lisheng Hu Xianwei Luo Xilian Gu Zhaolin
（Institute of Building Technology and Built Environment，School of Human Settlement and Civil Engineering，Xi′an Jiaotong University，Xi′an，710049，China）

Phase⁃change heat⁃storage material（PCM） is widely used in many fields，and its thermophysical properties are the key factor for its application．In this study，an improvement of theT⁃history method is presented，based on the basic principle of theT⁃history curve method，the theoretical step curve of the PCM and the actual step⁃curve measurement process．Firstly，according to crystalline⁃melting thermodynamic conditions，a certain degree of supercooling is necessary for crystal crystallization；therefore，there is sensible heat between the phase⁃change⁃start phase and the phase⁃change⁃end phase．Then，the energy⁃balance equation was improved by considering the sensi⁃ble heat effect on the energy⁃balance equation in the phase⁃change stage，and the temperature⁃difference effect on the energy⁃balance e⁃quation in the cooling process of the phase⁃transition phase．Secondly，the phase⁃change material was placed in a constant⁃temperature water source at 70 ℃ until it melted．Then，it was placed in a constant⁃temperature box at 10 ℃ ．The step curve was obtained with a two⁃second interval measurement．Finally，the experimental results for three phase⁃change materials，sodium dodecahydrate disodium phos⁃phate，lauric acid，and stearic acid，were calculated according to the improved equations to verify the improvement of theT⁃history meth⁃od．The results show that the calculated value of the latent heat is closer to that of the differential⁃scanning calorimetry process，and the error is less than 10% ．Therefore，the improvement of theT⁃history method has a certain practical significance for the development and testing of phase⁃change thermal energy storage material．

T⁃history method；phase change；latent heat

Wang Zanshe，male，associate professor，School of Human Settle⁃ment and Civil Engineering，Xi′an Jiaotong University，＋ 86 29⁃83395100，E⁃mail： wangzs＠ xjtu．edu．cn．Research fields：Building energy⁃saving technology，renewable energy utilization．

TB34；TK124

A

0253－4339（2017）06－0034－06

10.3969 /j.issn.0253 － 4339.2017.06.034

国家自然科学基金（51478386）资助项目。（The project was supported by the National Natural Science Foundation of China （No．51478386）．）

2017年5月4日

王赞社，男，副教授，西安交通大学人居环境与建筑工程学院，（029）83395100，E⁃mail：wangzs＠ xjtu．edu．cn。 研究方向：建筑节能、可再生能源利用。