气体边界层对平面液膜的稳定性影响

衣 然，覃粒子

(北京航空航天大学 宇航学院， 北京100191)

气体边界层对平面液膜的稳定性影响

衣 然，覃粒子

(北京航空航天大学 宇航学院， 北京100191)

利用线性化方程处理，分别以线性型、二次函数型以及修正的Stokes型3种不同的气体速度型对自由平面液膜进行了稳定性分析，并与无黏气体进行了对比；结果表明，修正的Stokes速度型与已有文献中的实验结果吻合最好，且液膜的稳定性随边界层的厚度增大而提高。考虑气体黏性能够提高对平面液膜稳定性分析的准确性。

平面液膜；黏性气体；边界层速度型模型；线性稳定性分析

自由平面液膜进入气体环境下的稳定性研究在造纸[1]、薄膜淋涂[2]等行业中有广泛的应用价值，并对发动机燃烧室中的喷雾燃烧[3]有着重要的基础研究意义。这是由于喷雾质量对发动机燃烧效率尤为重要，而液流破碎雾化的先期就是由射流的不稳定性所引发。平面液膜拥有较为简单的几何结构，其不受视线遮挡的特点使其更易在实验中展现其表面的波动情况及破裂阶段与相应特征。对于更常见的环形液膜来说，平面液膜是其曲率半径趋近于无穷大时的极限情况，但从不稳定的发展阶段和破裂特点来看，二者并没有本质的区别[4]。因此，理论分析的相对简单性和实验观测的清晰性导致平面液膜的不稳定性自20世纪50年代以来一直是众多学者的研究方向[5-8]。通过总结前人的研究结果，可以对平面液膜的稳定性给出以下简要的结论：① 平面液膜的失稳状态分为反对称和对称两种模式，而失稳的主导模式是要根据流体的物性参数及流动条件决定的；② 平面液膜失稳的主要原因是气、液界面的速度差异引致的；③ 液体的黏性对液膜的稳定性具有重要影响，且在大多常见物性条件下，黏性主要起到了抑制失稳的作用；④ 气体的可压缩性会对液膜的失稳有促进作用，尤其是在气体马赫数超过0.3后，这一促进作用愈加明显。

为了简化计算，气体的黏性常在理论计算中被忽略，这是由于液体的黏性与之相比对液膜的稳定性影响显著[9]。但实际上气体的黏性仍会对气液界面的相互作用产生一定影响，且更能反映真实的物理情况。但受到实验手段的制约，难以精确得到气体的边界层速度型，因此需要对气体速度型进行理论建模。本文考虑了气体的黏性，并针对3种不同的气体边界层速度型分析它们对平面液膜稳定性的影响。其中，在利用修正的Stokes速度型时，改进了Tammisola等[1]提出的速度型方程从而使边界层随空间的变化更能符合实际的物理意义。在求解控制方程及边界条件时，采用谱方法进行数值编程计算，得到了相应气体速度型下液膜的色散曲线。最后比较了无黏气体下的结果，并与文献中的实验结果进行对比分析。

1 物理模型及控制方程

取图1所示的液膜反对称扰动物理模型，由于本文所讨论的气体速度范围远小于声速，因此气、液两相均视为不可压缩流体。

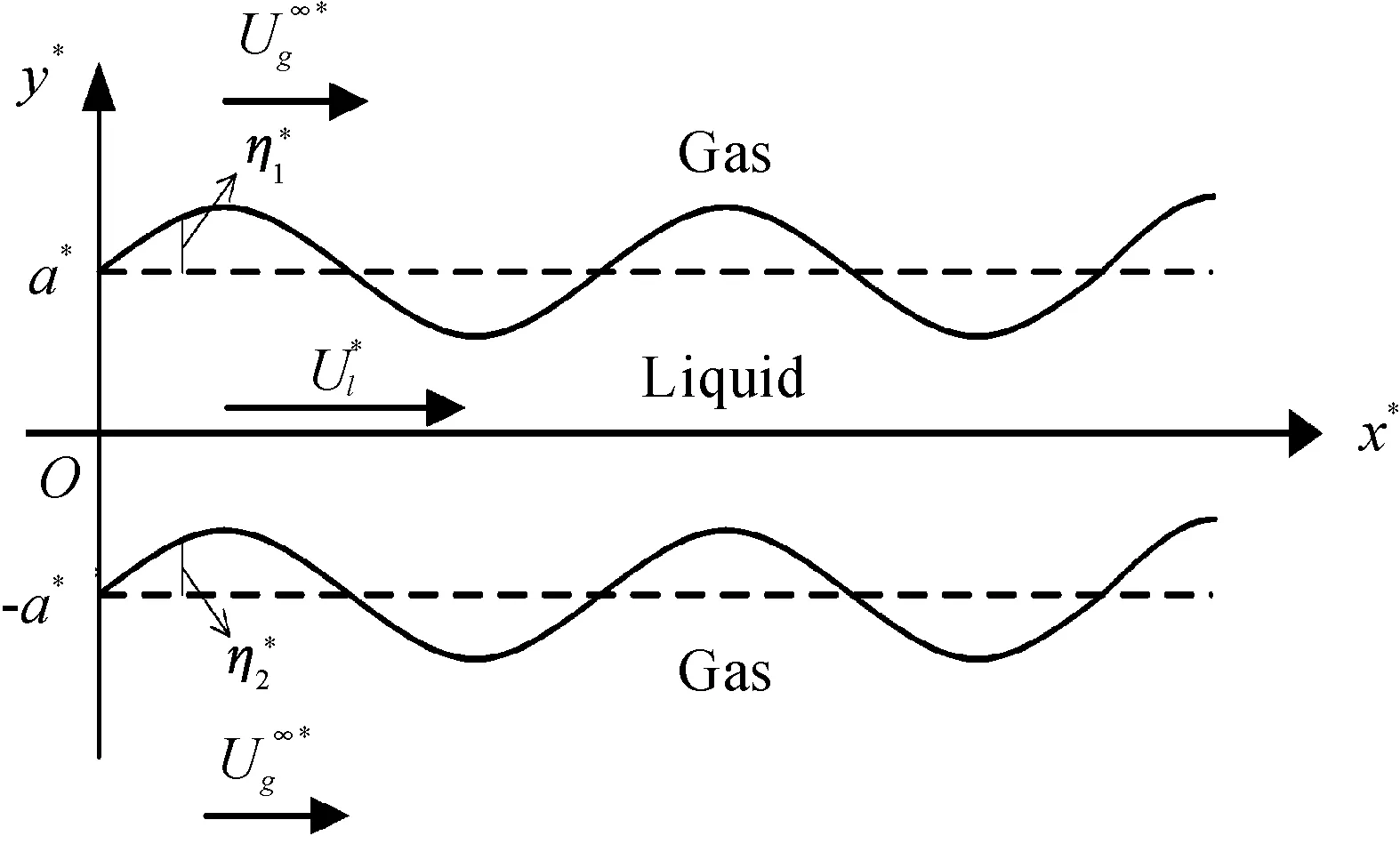
图1 二维平面液膜物理扰动模型

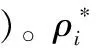
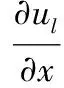
(1)

(2)

(3)

对于气体，即ylt;-1 orygt;1时，无量纲线性控制方程为：

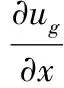
(4)

(5)

(6)

设扰动表面的位置为y=(-1)j+1+ηj(x,t)，其中j=1与j=2分别代表液膜的上下表面。则气、液界面的无量纲线性运动边界条件为

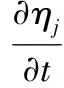
(7)

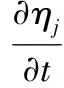
(8)

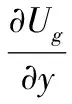
(9)

气、液界面的无量纲线性切向应力边界条件为

(10)

气、液界面的无量纲线性法向应力边界条件为：

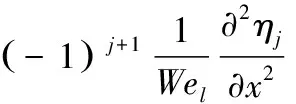
(11)

其中，无量纲数如表1所示。

表1 无量纲数定义

2 气体边界层的速度型

图2给出了气体在边界层内的速度型示意图，仿照平板边界层中的边界层位移厚度定义，液膜上气体边界层的厚度定义为

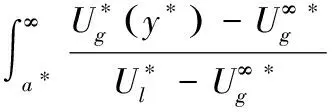
(12)

2.1 线性速度型

将气液界面的边界层视作二维平板来流经典问题的解的特殊形式。此时可根据卡门动量积分方法对不同边界层进行求解计算。设线性速度型下的边界层厚度为δ*，液膜两侧的气体轴向速度为

(13)

根据边界条件

(14)

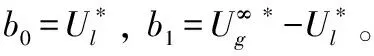
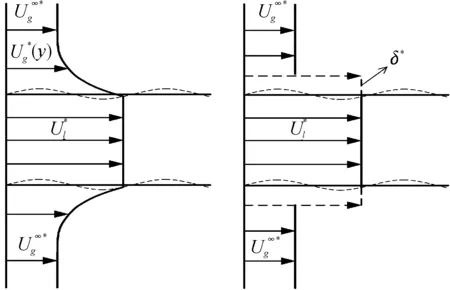
图2 气体边界层速度型示意图

根据卡门动量积分方法，将均匀来流与静止平板间的边界层增长规律转化为气体与平面液膜间的边界层增长规律，且平面液膜的上下两面对称。此时，由边界层厚度表达式可以得到

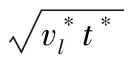
(15)

(16)

其中t*为特征时间，与气液相对速度有关。

2.2. 二次函数速度型

设边界层内二次函数型的气体轴向速度表达式为

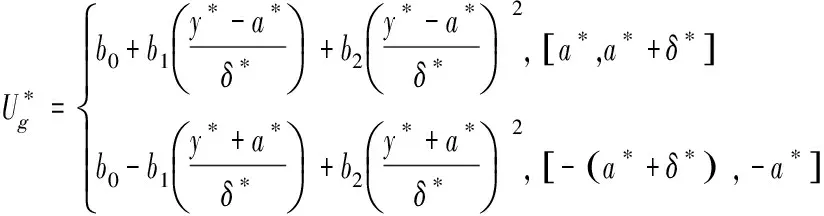
(17)

在计算边界条件时，除了要满足式(14)外，还需满足

(18)

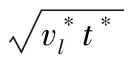
其中t*为特征时间，也与气液相对速度有关，即给出。

2.3 修正的Stokes速度型

Söderberg等[10]将Stokes第一类问题的解延伸，并给出气体速度型为

(19)

其中：erf代表误差函数；η为无量纲数，即

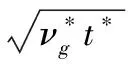
(20)

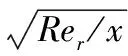
(21)

3 线性稳定性分析

采用线性稳定性方法进行求解。线性流体力学方程组具有简正模态形式的解：

(22)

其中：k为实数，代表液膜扰动波数；ω=ωr+iωi为复数，其中实部ωr代表增长率，虚部ωi代表了波动频率。注意，由于在计算中取反对称扰动模式，则有η1=η2。

3.1 气体无黏

D(ω,k)x=0

(23)

则问题的实质为求解方程具有非零解的条件特征值问题，即令|D(ω,k)|=0。在正弦模式下，解得无量纲色散方程为

(24)

3.2 气体有黏

仍采用式(22)所示的扰动形式。当气体有黏时，由于气体速度型的存在，使得此时无法获得解析解，而只能依靠数值计算的方法进行计算。这里采用Ye等[11]所述的谱方法，并基于Matlab实现数值计算过程，从而求解出给定K下对应的Ω值。

4 结果分析

图3为按照Tammisola等[1]给出的实验工况参数下的3种气体速度型的色散曲线对比图，其中散点为实验数据，虚线为气体无粘时的计算结果。在液膜轴向距离x=600下，当考虑气体粘性时，线性型对应的增长率最小，二次函数型次之，修正的Stokes型最大。且Stokes速度型对应的色散曲线与实验测量结果最为接近，这与Tammisola等[1]给出的结论一致，因此本文以Stokes速度型作为理论计算结果的最准确解。相比较气体无黏情况，可以发现，气体黏性能够抑制液膜的失稳，且气体速度型的区别所带来的色散曲线的差异远小于忽略气体黏性时所带来的差别，即考虑气体黏性时不论采用何种的速度型，都会减小气体无黏时的计算误差。因此在计算中采取形式较为简单的线性、二次函数型速度型[12]也能取得与实验计算接近的计算结果。

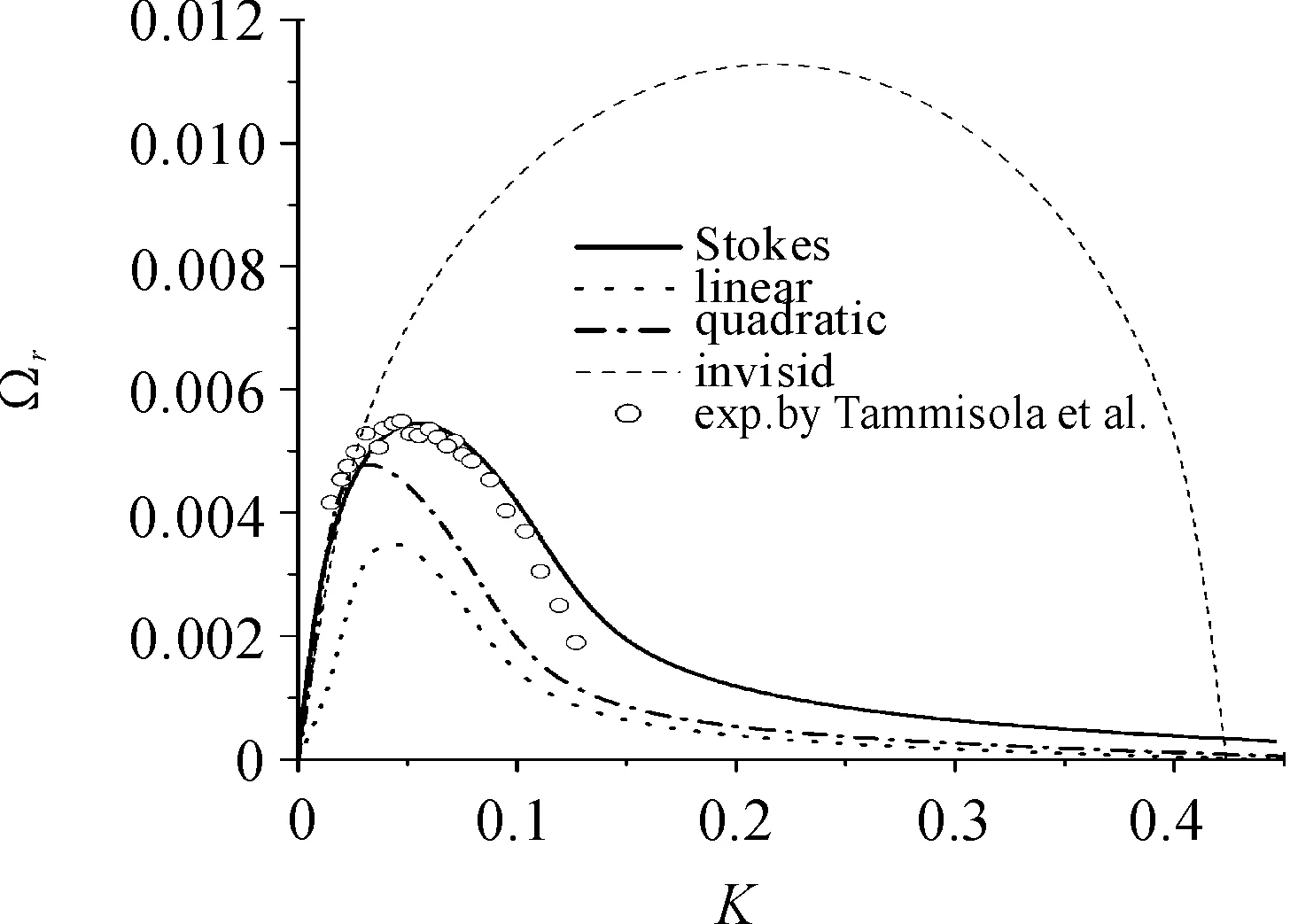
图3 平面液膜进入静止气体环境下，理论色散曲线与实验对比结果，包括考虑气体粘性的3种速度型以及无粘气体的计算结果。其中Rel=2 910，液膜无量纲轴向距离为x=600

由于主导波数对应的最大增长率代表了此波长在液膜表面波动中的增长速率最快，因此常被作为一个重要的特征参数。图3给出了在不同轴向距离(x=200,400,…,1 800,2 000)下，3种速度型所对应的最大增长率Ωrm与其无量纲边界层厚度δ的关系。可以看到，3种速度型下，Ωrm均与δ-1/2基本成正比关系，表明对同一种速度型而言，边界层越厚，增长率越小，液膜越稳定，且Stokes速度型对应的斜率最小，在对应x较小处(此工况下约为x=100)时，其最大增长率会被二次函数型反超。从这一角度来说，只有给出液膜轴向位置(或边界层厚度)的前提下，讨论线性、二次函数型相比理论准确解Stokes速度型而言的稳定性，才是有意义的。

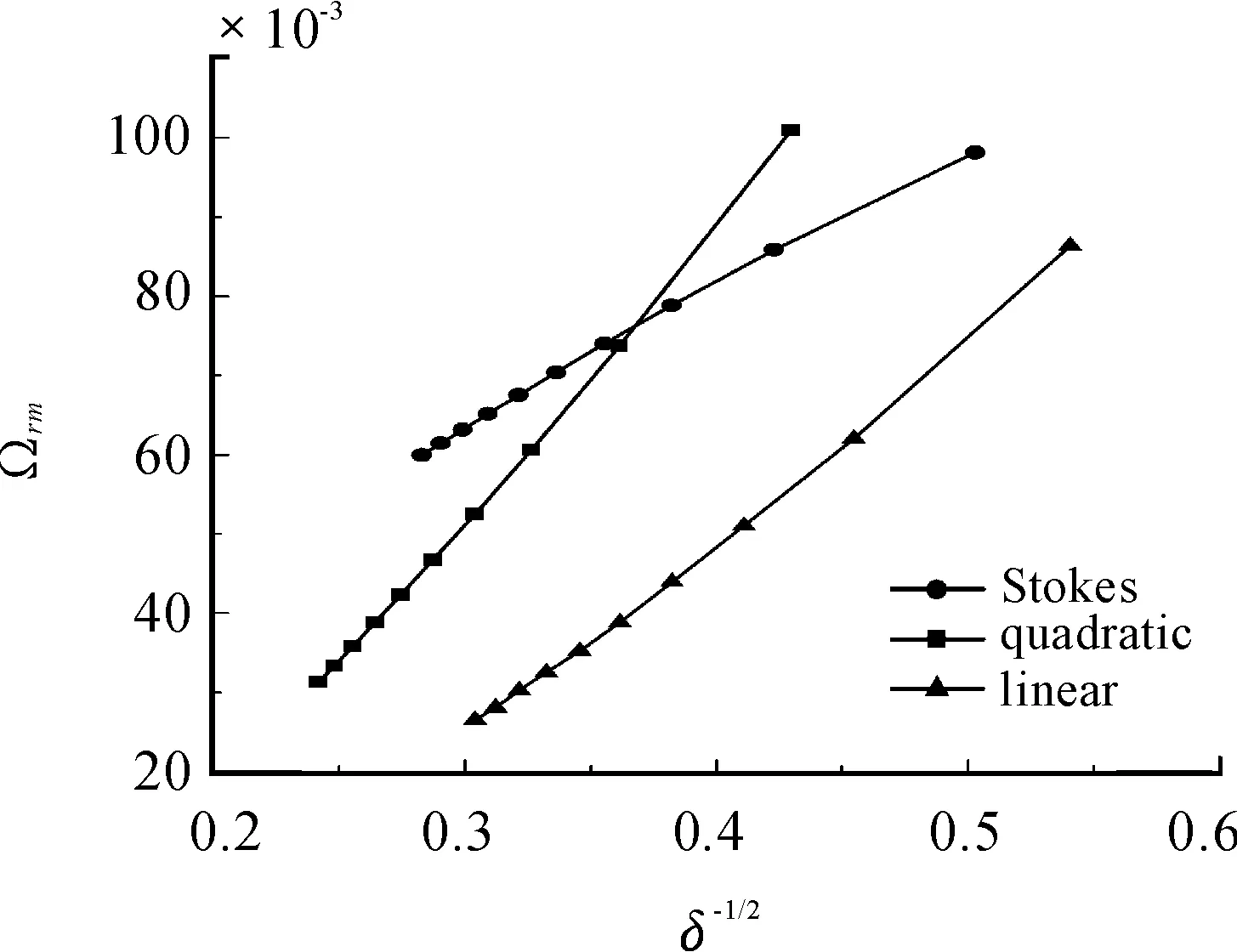
图4 平面液膜进入静止气体环境下，3种气体速度型下的最大增长率与不同轴向位置处(x=200,400,…,1 800,2 000)对应的边界层厚度δ的关系其中Rel=2 910。

5 结论

1) 修正的Stokes速度型与文献实验对比结果最好。

2) 在气体有黏情况下，速度型模型之间带来的增长率的差异远小于与气体无黏结果的差异，证明了气体黏性在准确计算色散曲线时的重要作用。

3) 同一种速度型下，液膜的稳定性随着气体边界层厚度的增大而提高。

[1] TAMMISOLA,OUTI,SASAKI,et al.Stabilizing effect of surrounding gas flow on a plane liquid sheet[J].Journal of Fluid Mechanics,2011,672:5-32.

[2] DYSON R J,BRANDER J,BREWARD C J W,et al.Long-wavelength stability of an unsupported multilayer liquid film falling under gravity[J].Journal of Engineering Mathematics,2009,64(3):237-250.

[3] CAO J,LI X.Stability of plane liquid sheets in compressible gas streams[J].Journal of Propulsion amp; Power,2012,16(4):623-627.

[4] LOZANO A,GARCI AOLIVARES A,DOPAZO C.The instability growth leading to a liquid sheet breakup[J].Physics of Fluids,1998,10(9):2188-2197.

[5] SQUIRE H B.Investigation of the instability of a moving liquid film[J].British Journal of Applied Physics,1953,4(6):167.

[6] LI X,TANKIN R S.On the temporal instability of a two-dimensional viscous liquid sheet[J].Journal of Fluid Mechanics,1991,226:425-443.

[7] 曹建明.液体喷雾学[M].北京：北京大学出版社,2013.

[8] ZANDIAN A,SIRIGNANO W A,HUSSAIN F.Three-dimensional liquid sheet breakup:vorticity dynamics[C]//Aiaa Scitech.[S.l.]:[s.n.],2015.

[9] IBRAHIM E A.Effects of compressibility on the instability of liquid sheets[J].Chemical Engineering Communications,1997,161(1):25-44.

[10] SÖDERBERG L D,ALFREDSSON P H.Experimental and theoretical stability investigations of plane liquid jets[J].European Journal of Mechanics-B/Fluids,1998,17(5):689-737.

[11] YE H Y,YANG L J,FU Q F.Spatial instability of viscous double-layer liquid sheets[J].Physics of Fluids,2016,28(10):167-282.

[12] LOZANO A,BARRERAS F,HAUKE G,et al.Longitudinal instabilities in an air-blasted liquid sheet[J].Journal of Fluid Mechanics,2001,437(437):143-173.

(责任编辑周江川)

TheEffectofGasBoundaryLayerontheInstabilityofaLiquidSheet

YI Ran， QIN Lizi

(School of Astronautics, Beihang University, Beijing 100191, China)

The effect of viscous air on the stability of a planar liquid sheet was studied. Three velocity profiles (linear, quadratic and modified Stokes models) were combined separately with linear instability analysis. Dispersion curves of the three conditions were compared with experimental data in former literature, and the inviscid air result was referenced as well. It is shown that the modified Stokes velocity profile yields excellent agreement with experimental data. Besides, for all three boundary velocity profiles, the instability of liquid sheet improves with the increase of the boundary thickness. Taking the gas viscosity into consideration can stabilize the sheet and improve the accuracy of the calculation result.

planar liquid sheet; viscous gas; boundary velocity profiles; linear stability analysis

2017-06-29；

2017-07-25

衣然(1993—)，女，硕士研究生，主要从事流体稳定性分析及雾化研究。

覃粒子(1978—)，男(土家族)，副教授，主要从事气液两相流流动、超声速喷管内流动与型面设计、脉动燃烧与脉冲喷气推进研究。

基础理论与应用研究

10.11809/scbgxb2017.11.043

本文引用格式：衣然,覃粒子.气体边界层对平面液膜的稳定性影响[J].兵器装备工程学报，2017(11):197-200.

formatYI Ran，QIN Lizi.The Effect of Gas Boundary Layer on the Instability of a Liquid Sheet[J].Journal of Ordnance Equipment Engineering,2017(11):197-200.

O659

A

2096-2304(2017)11-0197-04