复合斩波电路在二极管箝位型三电平逆变器中的应用

王笑宇，李自成

(成都理工大学 工程技术学院， 四川 乐山 614000)

复合斩波电路在二极管箝位型三电平逆变器中的应用

王笑宇，李自成

(成都理工大学 工程技术学院， 四川 乐山 614000)

在介绍二极管箝位型三电平逆变器的拓扑结构及工作原理的基础上，对三电平逆变器PWM控制方法进行分析，在Matlab/Simulink环境下搭建了三电平逆变器的模型，对几种载波PWM控制方法进行仿真并分析了仿真结果，针对存在着直流电压利用率比较低，总谐波畸变率高和中点电位不平衡等问题，采用复合斩波电路并结合以非正弦波作为调制波的PWM控制方法对三电平逆变器控制，仿真结果验证了所选用方法的有效性。

三电平逆变器；二极管箝位；载波层叠；复合斩波电路；中点电压平衡；Clark变换

1 二极管箝位型三电平逆变电路结构

在传统的二电平三相桥式逆变器中，输出的相电压只有两个电平状态，该电压波形的谐波含量高，电磁干扰比较严重。如果使逆变器电路的输出相电压有3种及3种以上的电平状态，则既能减少开关器件的电压应力，又能减少输出电压谐波含量，这种逆变电路就是多电平逆变电路[1-2]。由于电平数增加，输出波形阶梯增多，降低了输出电压的跳变；就可更加接近目标调制波(一般为正弦波)，在同样的开关频率下，多电平电路输出的谐波分量低于两电平电路的输出，这在大功率逆变器应用中尤为重要[3-4]。

二极管箝位型三电平逆变电路主电路如图1所示，通过辅助开关管和箝位二极管的共同作用，可以使逆变电路输出+Ud/2、-Ud/2、0三种电平的相电压，线电压则为五电平。与二电平电路输出线电压波形比较，三电平电路输出线电压谐波含量更小，波形更接近正弦波[5-6]。

图1 二极管箝位型三电平逆变电路结构

2 三电平逆变器控制方法

三电平逆变器常用的控制方法有正弦波调制PWM法、电压空间矢量PWM调制法，其中电压空间矢量PWM调制法的主要缺点是控制算法复杂，不利于工程实际应用。正弦波脉宽调制法的原理是通过调制波与载波进行比较，由它们的比较结果得到对应的开关脉冲控制信号，将直流电压转化成特定形状的脉冲电压序列。以此实现变压、变频，并能够将谐波有效地进行抑制[7-8]。其中常以正弦波为调制波。把多个频率和幅值一样的三角载波上下层叠起来，然后用调制波分别与上下层叠的各个载波相比较，以此产生多电平PWM脉冲。载波层叠有同相层叠、反相层叠和载波交叠的PWM控制、梯形波为调制信号的PWM控制等方法。

3 仿真实验结果分析

用Matlab的Simulink模块搭建仿真模型如图2所示。其中PWM载波部分封装在Level 3 Pwm子系统内，二极管箝位型三电平逆变电路分装在3 Level子系统内。分别采用载波同相、反相、交叠和梯形波为调制信号的PWM控制方法。参数设置如下：直流源Ud=100 V，C1=C2=1 F。正弦调制波的频率=50 Hz,调制度m的值设为0.85，三角载波频率1 950 Hz。负载为阻感性，R=2 Ω，L=0.02 H。仿真时间设为0.6 s。因采用以上各种控制方式逆变器所输出的线电压均为五电平PWM波形，所以仅列出载波同相层叠控制方式的线电压Uab波形如图3所示。各种控制方式产生的线电压Uab的频谱分析分别如图4～图7所示。

图2 三电平三相PWM逆变器仿真模型

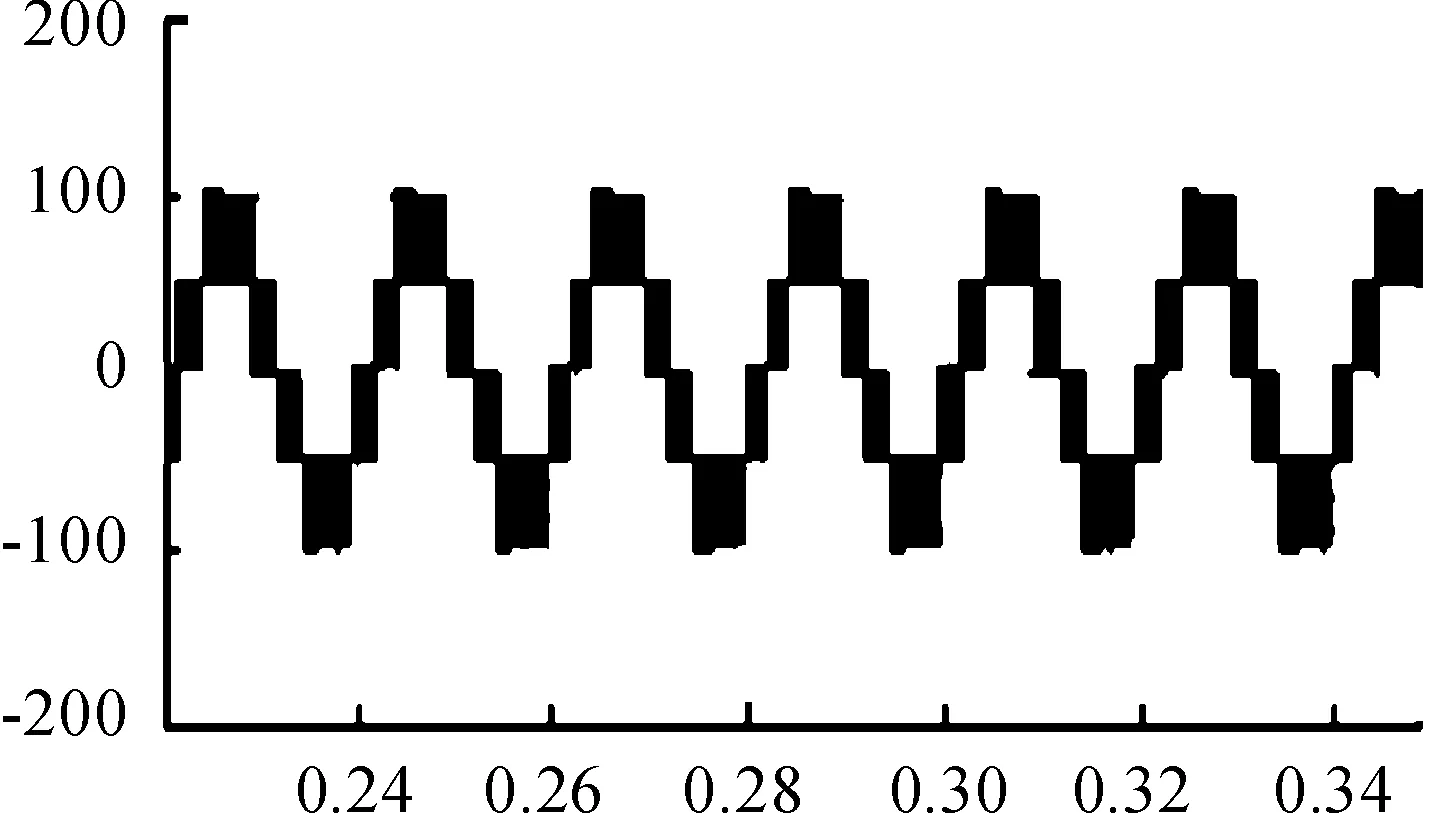
图3 载波同相层叠线电压Uab波形

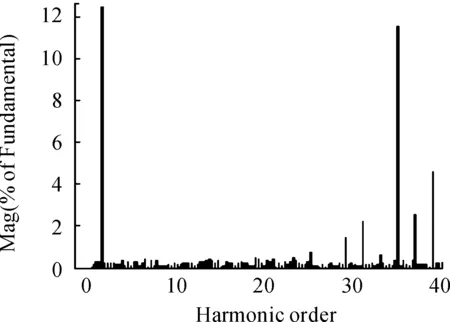
图4 载波同相层叠线电压Uab频谱分析

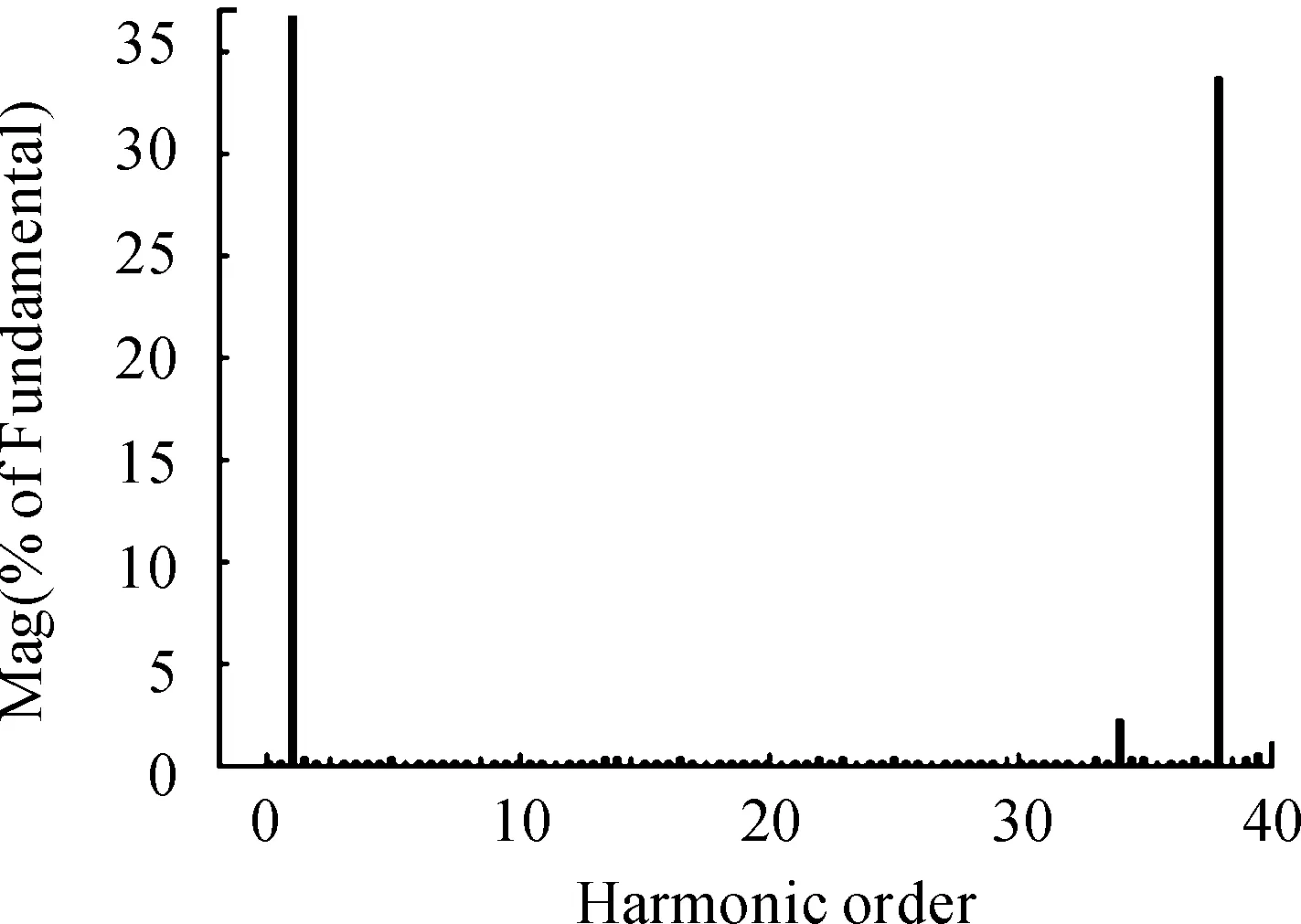
图5 载波反相层叠线电压Uab频谱分析

考察二极管箝位型多电平逆变器控制方法的优劣，主要分析用该方法控制逆变器输出的电压(电流)波形的总谐波畸变率、直流电压利用率及中点电位是否平衡等指标，而且这些指标要综合考虑。把输出的线电压频谱都分析到40次谐波。从图6～图7看出，载波交叠和梯形波为调制信号的PWM控制法，其线电压Uab的基波电压幅值相对较高，因而直流电压利用率较大，但所含谐波较大，不适合用于对二极管箝位三电平逆变器的控制。对于载波反向层叠，存在以载波整数倍频率为中心的边带谐波，幅值较大。同相层叠法电压的总谐波畸变率(THD)为13.01%最小，对于同相叠成法，在三相系统的线电压中，其线电压由于所用载波是同相位载波，谐波在三相系统中相互抵消，输出的线电压比反相法的波形质量要好，更接近正弦波，因此同相层叠对于波形的控制及改善效果较好。但也存在着一些不足之处，如直流电压的利用率比较低，没有考虑直流侧电容电压不平衡等问题。

图6 载波交叠线电压Uab频谱分析

图7 梯形波为调制信号线电压Uab频谱分析

4 采用非正弦调制波和复合斩波电路的控制方案

为了解决直流电压的利用率比较低，采用改变调制信号波的控制方法，即在正弦调制波中注入零序分量，对于一个三相系统，这个零序分量是三相正弦波瞬态最大值和最小值的平均值。这样使正弦波成为类似马鞍形的非正弦波，采用此非正弦波作为调制波，载波仍为等腰三角形的同相层叠PWM控制方案。以降低开关频率，提高电压利用率，改善输出波形质量。非正弦波作为调制波的PWM控制方案如图8所示。

直流侧中点电压不平衡的原因及电容电压调整的复合斩波电路设计

三电平逆变器处于理想工作状态时，直流侧的两个电容C1、C2上的电压应保持相等，通过对上述选用几种PWM控制方式的电容电压检测发现，每种控制方式的两个电容电压均不相等，中点电压存在不平衡现象，其中采用载波交叠法时电压偏差量最大。本文列出载波同相层叠法两个电容C1、C2上的电压波形如图9所示。

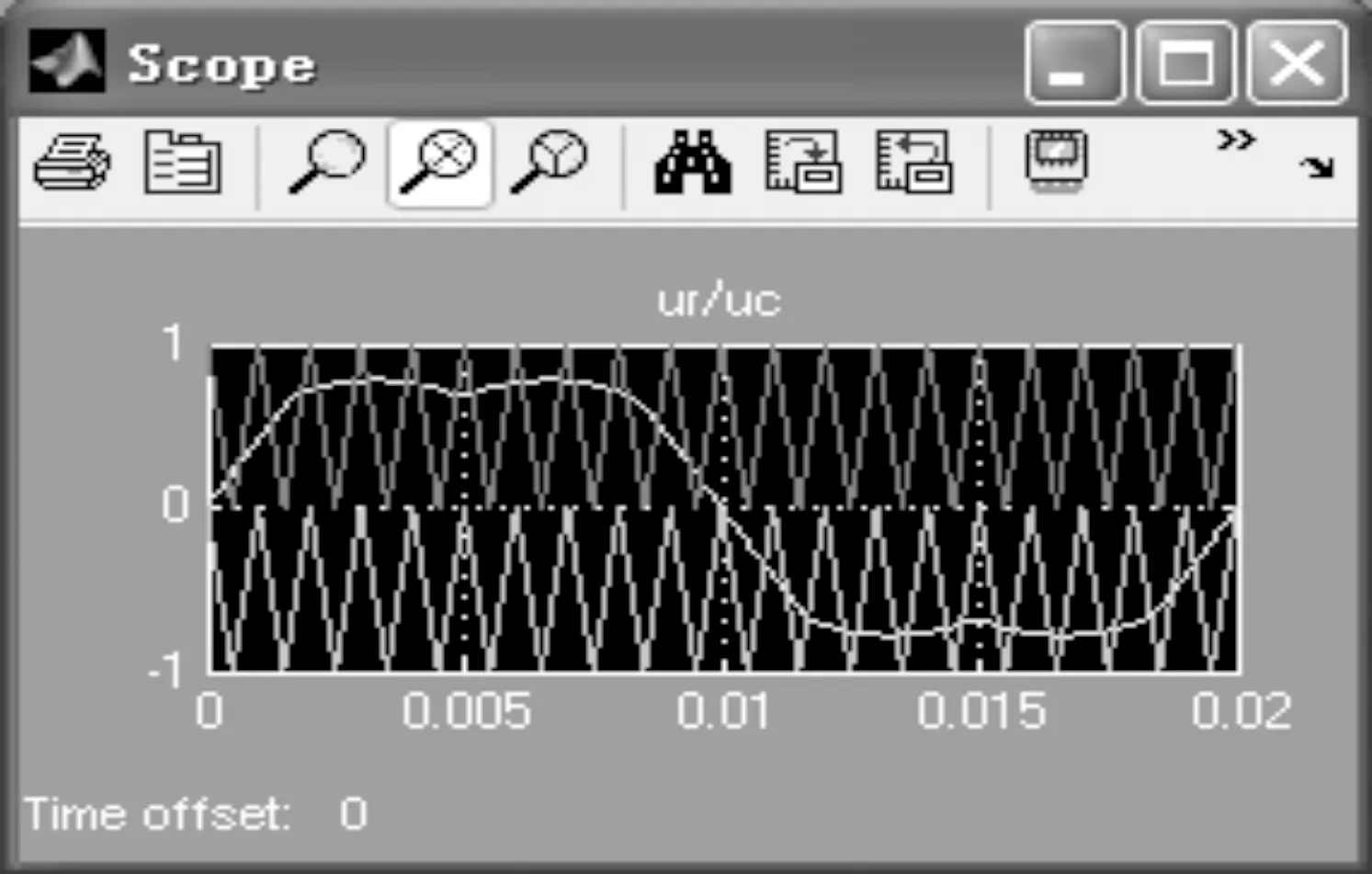
图8 非正弦波作为调制波的PWM控制

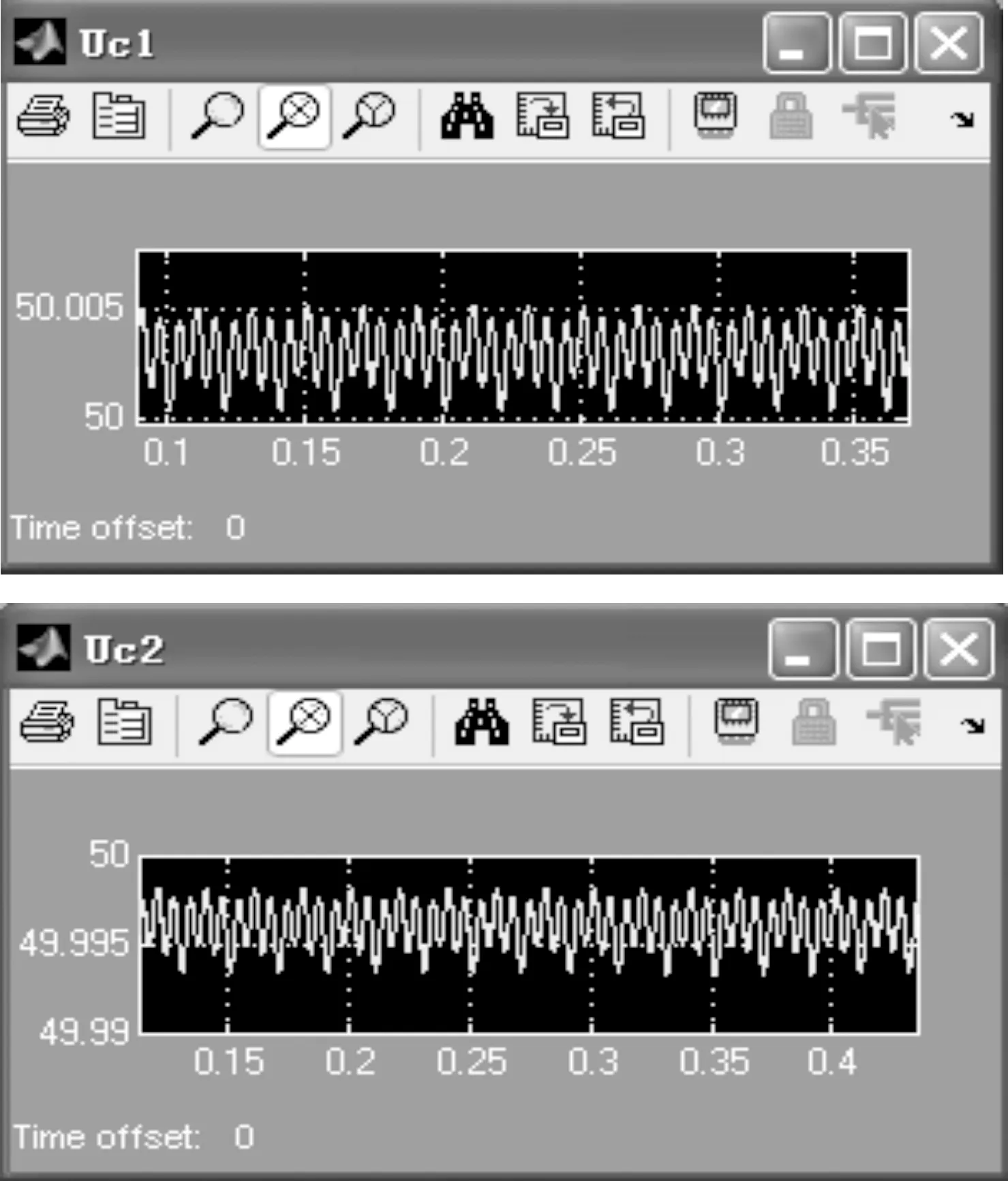
图9 载波同相层叠PWM调制法Uc1与Uc2波形

从图9可以看出Uc1在50 V以上波动，偏大，Uc2在50 V以下波动，偏小，这样就造成中点电压不为零。出现这种现象的原因是：当三电平逆变器采用PWM的控制方法时，由于每个桥臂有3个电平，总共可以得到33=27个空间矢量，可将这27个矢量分为四类：长矢量、中矢量、短矢量和零矢量[9-10]。其中中矢量和短矢量至少有一相输出和零母线相连，并和正(负)母线形成电流回路，从而导致电容C1和C2的充放电，中点电压就会偏离零电位[11]。当两个分压电容上的电压不相等时，逆变器输出的电压波形质量下降，甚至发生畸变，从而可能会损坏直流侧电容及开关器件[12-13]。欲使该逆变器电路工作在比较理想的状态，就需要保持两个分压电容上的电压相等，实时对直流侧电容电压调整并维持电压基本恒定非常重要[14]。所以选用由复合斩波电路对用非正弦波作为调制波的PWM控制的三电平逆变器进行电容电压调整，其工作原理如图10所示；其中V1、V2是为IGBT，D1、D2为续流二极管，L1、L2为储能电感，C1、C2为直流侧分压电容，Gate Drive1、2是触发信号发生器。为使斩波电路工作在电流连续状态下，电路参数设置：L1=L2=1H，触发脉冲信号频率取为6 kHz，占空比80%。该调整电路工作原理是： 因直流电源Ud一般情况下保持不变，且Uc1+Uc2为一常数。所以Uc1增加必然会导致Uc2下降，反之Uc2下降也会使Uc1增加。

图10 带复合斩波调整电路的三电平逆变器

在逆变器工作中，如果Uc1gt;Uc2，经逻辑比较器的比较输出高电平，驱动开关管V1导通；V2关断。此时V1、L1、C2、D1与直流电源Ud组成斩波电路开始工作。运行中电容C2处于充电状态，电压上升，且此时电感L1吸收电能。当电容C2充电达到一定程度后，断开开关管V1，使得D1、L1、C2闭合形成回路。此时电感L1上储存的电能对电容C2进行充电，从而使得电容C1、C2上的电压逐步趋向相等。同理，当Uc1lt;Uc2时，驱动开关管V2导通，V1关断。此时，V2、L2、C1、D2与直流电源Ud组成斩波电路工作。运行中电容C1充电，电压上升，电感L2吸收电能。当电容C1充电达到一定程度后，断开开关管V2，使得D2、L2、C1闭合形成电流回路。此时电感L2上储存的电能对电容C1充电，从而使得电容C1、C2上的电压逐步趋于相等。加入调整电路运行后电容电压的波形如图11所示。

从图11可以看出，经过调整后Uc1、Uc2均在50±0.000 2 V之间波动，两个电容上的电压值基本相等。在图12中显示采用调整电路后的线电压Uab频谱分析，与图4～图7对比看出总谐波畸变率(THD)明显减少，线电压Uab的基波电压幅值比正弦调制波脉宽控制有较大增加。另外根据空间矢量变换的可逆性，空间电压矢量U的顶点的轨迹越趋近于圆，则原三相电压越趋近于三相对称正弦波，三相对称正弦电压是理想的供电方式，也是逆变器输出电压的追求目标[14-15]，所以把逆变器输出的三相相电压经Clark变换后，得到图13所示的空间电压矢量运动轨迹图，基本上是一个圆。

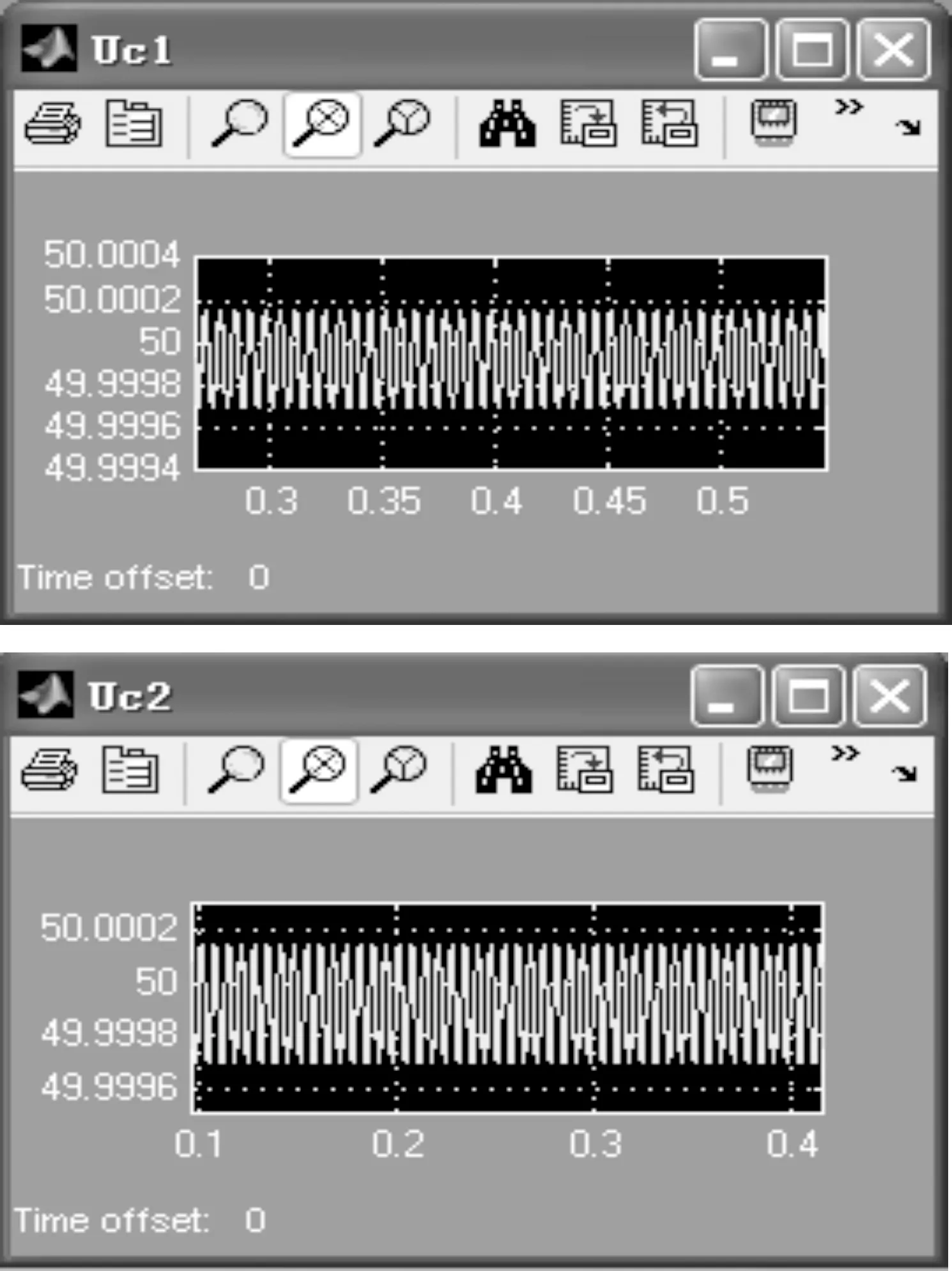
图11 带复合斩波调整电路的非正弦调制波PWM控制三电平逆变器电容电压波形

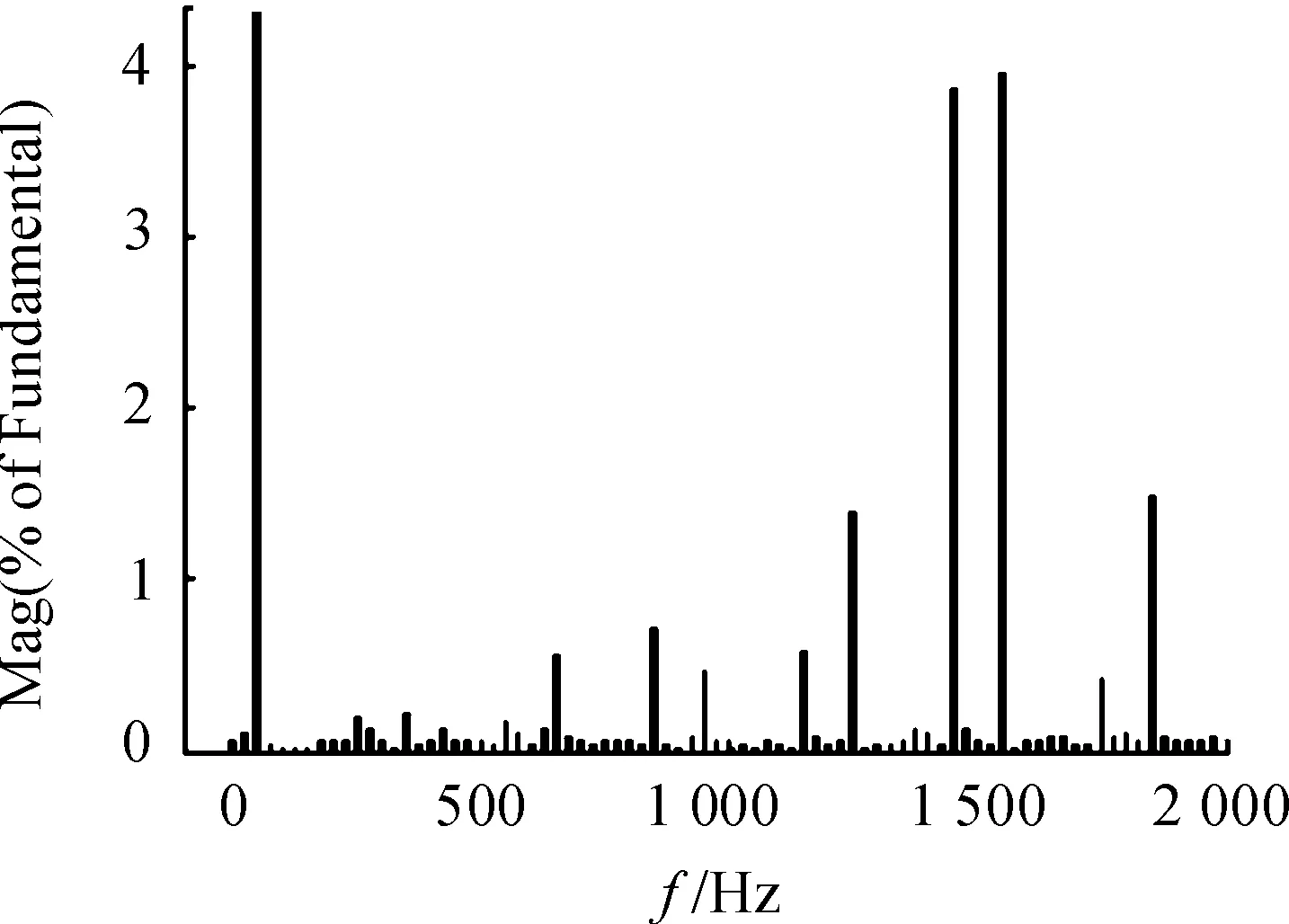
图12 带复合斩波调整电路调整的线电压Uab频谱分析

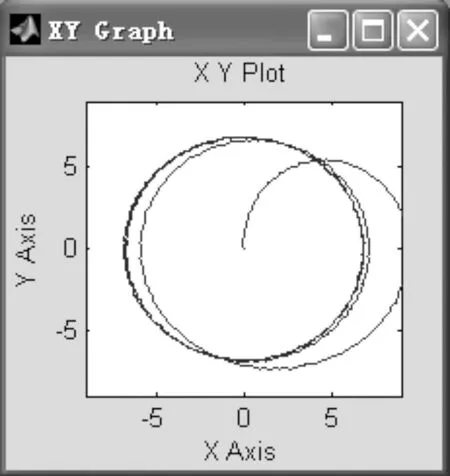
图13 Clark变换后电压矢量运动轨迹

5 结论

衡量多电平逆变器控制方法是否合理，往往是多个输出指标综合评价的结果，通过对本文列出的几种控制方法输出结果进行分析比较后，尽管载波交叠、梯形调制波PWM控制方法有较高的直流电压利用率，但谐波含量大，所以它们不宜用于二极管箝位型拓扑结构，适用于H桥级联型结构的控制，当采用正弦调制波的同相、反相层叠PWM控制时，同相层叠有较小的谐波率，输出电压波形较好，但直流电压利用率相对较低，没考虑中点电压的不平衡问题，也不理想。所以针对上述存在的几个问题，采用非正弦波作为调制波，并结合复合斩波电路对中点电压平衡控制的方法。运行结果显示各项指标都比较理想，说明此法对二极管箝位型拓扑结构的控制效果比较好。

[1] 郭荣祥.电力电子应用技术[M].北京：高等教育出版社,2013.

[2] 周京华.现代电力电子技术[M].北京：中国水利水电出版社,2013.

[3] 林渭勋.现代电力电子技术[M].北京： 机械工业出版社,2015.

[4] 王卓，王振和.电力电子技术[M]北京：高等教育出版社2014.

[5] 徐德鸿.电力电子系统建模及控制[M].北京：机械工业出版社,2013.

[6] 谷鑫，姜勃.基于三次谐波控制及脉冲波动分析的三电平SHE-PWM调制优化策略[J].电工技术学报,2015(4):89-95.

[7] 周深渊.电力电子技术[M].3版.北京： 机械出版社,2016:200-260.

[8] 同向前.电压源换流器在电力系统中的应用[M].北京：机械出版社,2012:19-70.

[9] 李华德．现代交流调速系统[M].北京：机械工业出版社,2014:145-210.

[10] 曲永印，白晶.电力电子技术[M].北京：机械工业出版社,2013:60-142.

[11] 那日沙,周凯.电力电子、电机控制系统的建模及仿真[M].北京：机械工业出版社,2016:50-210.

[12] 张建光.基于改进粒子群算法的逆变器谐波优化研究[D].昆明：昆明理工大学,2016.

[13] 苏良成,戴鹏.三电平逆变器新型简化算法及其优化控制[J].电气传动.2015(1):25-28.

[14] 张兴.高等电力电子技术[M].北京：机械工业出版社,2015:35-235.

[15] 徐德鸿.现代电力电子学[M].北京：机械工业出版社,2013.

(责任编辑杨继森)

CompositeChopperCircuitintheApplicationoftheDiodeClampTypeThreeLevelInverter

WANG Xiaoyu， LI Zhicheng

(Engineering Academy, Chengdu University of Science and Technology， Leshan 614000, China)

It introduced the diode clamp type three level inverter topology structure and working principle, and on the basis of analysis of three level inverter PWM control method, it set up in Matlab/Simulink environment model of three level inverter. Several carrier PWM control methods are simulated and it analyzed the simulation results, for there is a dc voltage utilization ratio which is lower, and the total harmonic distortion rate is high and neutral voltage is imbalance. With composite chopper circuit and combining with non sine wave as the modulation wave PWM control method for three level inverter control, the simulation results verify the effectiveness of the chosen method.

three level inverter; diode clamp; carrier layer; composite chopper circuit; Midpoint voltage balance; Clark transformation

2017-06-25；

2017-07-25

国家自然科学基金资助项目(11375055)

王笑宇(1969—)，男，讲师，主要从事电力电子、检测技术与自动化装置研究。

信息科学与控制工程

10.11809/scbgxb2017.11.027

本文引用格式：王笑宇，李自成.复合斩波电路在二极管箝位型三电平逆变器中的应用[J].兵器装备工程学报，2017(11):124-128.

formatWANG Xiaoyu，LI Zhicheng.Composite Chopper Circuit in the Application of the Diode Clamp Type Three Level Inverter[J].Journal of Ordnance Equipment Engineering,2017(11):124-128.

TP277

A

2096-2304(2017)11-0124-05