基于aRVM的电子设备状态在线预测方法

高明哲,许爱强，许 晴

(1.海军航空工程学院 科研部, 山东 烟台 264001； 2. 91635部队， 北京 102200)

【信息科学与控制工程】

基于aRVM的电子设备状态在线预测方法

高明哲1,许爱强1，许 晴2

(1.海军航空工程学院 科研部, 山东 烟台 264001； 2. 91635部队， 北京 102200)

针对电子设备的状态预测问题，提出一种基于自适应核学习相关向量机的在线状态预测方法。所提方法将电子设备的状态预测视为一个有监督回归问题。首先通过设备离线数据的后验概率选择最适合预测问题的基函数，然后采用离线数据训练aRVM预测模型，最后在预测过程中通过对在线数据的增样学习来动态更新模型参数。仿真预测实例与实例预测实验的结果表明：所提方法相比传统方法显著提高了预测精度和在线训练效率。

电子设备；状态预测；相关向量机；在线训练；自适应核学习

电子设备在使用期间伴随着组成部件性能的退化往往会导致设备功能的下降、失效，甚至引起灾难性后果。这类退化过程通常具有内在的规律性，可通过预测方法对其健康状态进行预测从而实现对设备的视情维修，这对减少故障损失、降低维修费用具有重大意义[1]。现阶段一种有效的预测方法是通过对设备历史数据的时间序列进行趋势外推，从而得到未来时刻设备的健康状态[2]，这对数据序列的预测方法具有很高要求。文献[2-8]分别将隐马尔可夫链、灰色模型、最小二乘支持向量机、超限学习机和相关向量机等方法应用到电子设备的状态预测中，其中基于相关向量机(relevance vector machine,RVM)的预测方法不但在小样本训练下拥有参数设置简单、预测精度高的优势，并且能够给出预测结果的置信区间，具有广阔的应用前景[8]，近年来在诸多预测领域中获得了广泛关注[10-12]。然而现实中的电子设备是一个时变系统，传统RVM预测方法得到却的是一个参数恒定的离线预测模型[13]，这导致了预测精度会随着时间推移不断降低。面对不断更新的在线样本，传统RVM只能重新训练预测模型以保持动态预测能力，极大的降低了预测效率。

自适应核学习相关向量机(relevance vector machine with adaptive kernel learning,aRVM)是Tzikas等[14]在增量学习方法[15]和平滑稀疏度先验[16]的基础上提出的一种改进的RVM建模方法，相比传统RVM其主要改进在于：以增量学习的方式向模型中逐个添加训练样本，优化计算复杂度；各相关向量对应的核参数可取不同的值以适应数据的局部特征，模型的灵活更强。aRVM采用的增量学习方法能够在新样本加入时在原有模型的基础上快速更新模型参数，使得aRVM能够拓展到在线预测中。

由于在线预测对预测精度以及实时性都具有较高的要求，影响相关向量机预测精度的主要因素之一是预测模型所采用的基函数类型以及基函数中核参数的取值。虽然aRVM能够自适应求取最优核参数，但对基函数类型的选择缺乏明确的依据。鉴于此，本文对aRVM进行了改进，并提出一种基于aRVM的电子设备在线状态预测方法。所提方法首先补充了aRVM模型基函数的选择方法，在训练前根据离线样本的后验概率自适应选择最优基函数。然后在训练中针对在线样本进行快速的增样、减样学习来自适应更新核参数，在保持模型稀疏型的同时提高动态预测能力。最后以雷达发射机状态预测的仿真实验和音频放大器的实例预测实验对该方法的性能进行验证。

1 aRVM回归原理

1.1 aRVM的模型

aRVM的基本模型如下[14]：

φ(x;θi)

(1)

式(1)中：φ(x;θi)为基函数；ω=(ω1,…,ωN)T为基函数的权值；θi为基函数的核参数。区别于传统RVM，aRVM中各核参数θi可独立选取不同的值。

训练的目标是求得式(1)中各参数的值。由于训练后的权值ω大部分为零，因此，aRVM模型最终是由少数权值为非零的相关向量(relevant vectors,RV)组成的一个稀疏模型。

p(t|ω,β)=N(t|Φω,B-1)

(2)

式(2)中：Φ=[φ1,φ2,…,φN]T，为N×(N+1)维基函数矩阵，φi=[1,φ(xi;θ1),φ(xi;θ2),…,φ(xi;θN)]T；B=βI。

为防止过拟合，针对每个权值ω，aRVM赋予其对应超参数α=(α1,…,αN)T作为先验来控制模型的复杂度，二者满足高斯分布：

(3)

根据贝叶斯定理可得ω的后验概率满足高斯分布：

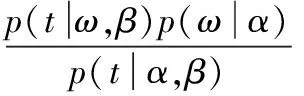
(4)

式(4)中：μ=ΣΦTBt，Σ=(ΦTBΦ+A)-1，A=diag(α)。

超参数先验概率p(t|α,β)的对数为：

L=logp(t|α,β)=

-1/2[Nlog2π+log|C|+tTC-1t]

(5)

式(5)中：C=B+ΦA-1ΦT。

aRVM对超参数α和β引入稀疏度先验p(α|β)来控制模型有效参数的个数以防止过拟合[14]：

p(α|β)=∝exp(-ctrace(S))

(6)

式(6)中：S=ΦΣΦTB称为平滑矩阵，矩阵S的迹trace(S)称为S的自由度，用以表示模型参数的有效个数；c为稀疏度参数，本文中取log(N)/2。

RVM将权值ω边缘化，从而使得模型的训练问题简化为求后验概率p(α,β|t)关于参数α、β及θi最大值的问题。由于p(α,β|t)∝p(t|α,β)p(α|β)p(β)，则根据式(5)、(6)可得到超参数后验概率p(α,β|t)的对数：

(7)

最终模型训练的结果便是求得使LS最大的最优超参数值[αMP,βMP,θMP]。

1.2 aRVM的训练

为优化计算复杂度， aRVM在训练前将模型中所有的超参数初始化为α→∞，β取var(t)×0.1作为初始值，核参数θ在分布区间内随机选取初始值。此时模型内参与运算的基函数集F为空。训练开始后，针对每个样本点，将其超参数αi设为[15]

(8)

(9)

核参数θi的最优值为LS(αi)对其偏导数为零的解，可通过拟牛顿法中的BFGS(Broyden Fletcher Goldfarb Shanno )方法来获得。

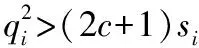
(10)

θi的更新值取θi=∂LS/∂φ(θi)=Dni，其中

D=B[(t-Φμ)μT-ΦΣ]+2cBΦΣAΣ

(11)

β则取偏导数

βctrace(ΣΦTΦ)

(12)

为零的数值解来更新[14]。

若更新后的出现αgt;1012的样本点，则由式(3)的先验约束可知该样本点对于预测模型的贡献趋于0，将其从F中剔除。遍历所有的离线样本之后，模型收敛得到一个稀疏的预测模型。

1.3aRVM的预测结果

模型训练完成后，得到超参数的最优值[αMP,βMP,θMP]。则对于新的输入x*，模型输出其目标值t*服从高斯分布：

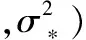
(13)

其均值和方差分别为：

y*=μTφ(x*;θMP)

(14)

(15)

2 aRVM的改进

虽然aRVM本身依然是一种面向固定样本的离线学习算法，但为减少训练的计算复杂度而采用的增量学习方式使得 aRVM能够拓展到在线训练。由于影响RVM预测精度的主要因素是基函数的类型以及核参数的值，而aRVM却缺乏相关的基函数选择方法，因此本文对aRVM作出两点改进：一方面通过在训练前根据离线样本的特点预先选择预测模型的基函数类型；另一方面通过对在线样本的增样、减样训练来自适应更新模型参数和核参数。

2.1 基函数的选取

在核方法中，不同的核函数具有的特性并不相同，使得在不同的应用场合，核函数的性能表现差异很大[18]。因此，基函数的选择是否合理对RVM的预测性能有直接影响。然而aRVM并没有给出基函数的选择方案，文献[14]人为设定了基函数的类型，实际应用中不具备推广性，而文献[19]采用了5折交叉验证方法确定基函数类型，极大的增加了模型的训练时间。

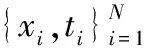
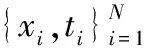
(16)

式(16)中：K为计算Monte-Carlo平均时的采样数；超参数在区间α∈[10-12,1012]、β∈[10-4,100]内均匀取值。

在得到各类基函数的后验概率LB后，取令LB最大的基函数作为训练基函数φMP，并将LB最大时基函数对应的核参数值作为迭代初始时的核参数值θini。基于离线样本后验概率的基函数选择方法无需反复进行测试，相比交叉验证方法能够大幅度减少计算复杂度。

2.2 在线参数更新

(17)

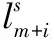
(18)

若满足学习条件：

(19)

则向当前模型的F中添加样本(xm+i,tm+i)对应基函数，并按照式(10)～式(12)来更新参数α、θ、β。

之后以减样的方式删除超参数αgt;1012对应的基函数，保持模型稀疏性并得提高预测性能。

若不满足式(19)的学习条件，则保持原有模型不变。当在线样本序贯加入时，重复上述学习过程，在模型收敛后得到各参数的最优值[αMP,βMP,θMP]，从而完成aRVM的在线训练。

在线训练的计算复杂度主要取决于过程变量Σ=(ΦTBΦ+A)-1中的求逆运算，传统RVM起始迭代时的计算复杂度为O(N3)，N为所有离线和在线训练样本的总数，而在线aRVM在参数更新时每步迭代的计算复杂度为O(M3)，M为参与运算的基函数集F中的样本数量，由于Mlt;lt;N，因此相比传统RVM，aRVM在线训练的计算复杂度大大降低。

3 电子设备的在线状态预测

反映电子设备运行状态的特征参量主要有电阻值、漏电流、输出电压、输出电流等[1]。采用aRVM对电子设备进行在线状态预测首先需要对特征参量序列进行相空间重构，构建输入样本与目标值的对应关系。

假设采集到的特征参数为一组随时间变化的序列{s(t)|t=1,2,…,l}(l∈R)，根据Takens定理[8]，可在一个高维相空间上恢复该序列的后续演化规律，即存在一个非线性映射f:Rd→R，使得

s(n)=f([s(n-1),s(n-2),…,s(n-d)])

(20)

式(20)中：d为相空间嵌入维数。

由此可构建aRVM训练的输入样本和目标值：

(21)

(22)

式(21)中：X为aRVM的输入样本；t为对应的目标值。利用该样本训练aRVM，使预测模型逼近非线性映射f，从而对后续数据{s(l+1),s(l+2),…}进行预测。基于aRVM的电子设备状态在线预测流程如下：

步骤1 离线采集设备的状态参量数据并按时间顺序进行相空间重构，生成aRVM的初始离线训练样本集；

步骤2 计算离线训练样本相对于各类基函数的后验概率，选择后验概率值最大的基函数作为训练基函数；

步骤3 将离线训练样本集输入到aRVM，训练后得到aRVM的初始离线预测模型；

步骤4 利用当前模型预测后续时刻的特征参量值，并将采集到的新数据输入到预测模型中判断是否满足在线学习条件；

步骤5 对于满足学习条件的新数据对其进行在线学习更新预测模型参数；

步骤6 根据预测模型得到状态参量最新的动态预测结果，从而判断被测设备后续的健康状况。

4 仿真实验

高压电源作为雷达发射机的核心部件，其运行状态直接关系到雷达发射机的可靠性。本文的仿真预测实验以某型雷达发射机的高压电源为对象，实验数据源于文献[1]中在雷达维修厂对该雷达发射机高压电源等时间间隔采样得到的40组纹波电压数据，见表1。

表1 纹波电压数据

由于电子设备采样数据间隔较大，在短期预测的研究上已有文献的研究成果主要集中于电子设备状态的一步预测[2,4-8]，因此本文实验也只针对一步预测。将aRVM的在线预测结果与基于优化算法的传统RVM[8]的预测结果进行对比，仿真实验在CPU为Intel Xeon E3-1230v3，16G内存的PC机上运行。相空间嵌入维数取5，重构后生成样本35组，将前15组作为离线训练样本。传统RVM采用高斯核作为基函数[8]， 本文方法从一阶多项式核(Poly1)、二阶多项式核(Poly2)、高斯核(Gauss)和Morlet小波核四类基函数中自适应选择基函数。四类基函数对应的后验概率如表2所示，同时给出采用5折交叉验证计算的四类基函数预测误差作为参照。从表中可以看出，后验概率的大小和预测误差有直接的关系，本次实验选择了后验概率最大的二阶多项式核作为预测模型的基函数。

表2 基函数对应的交叉验证误差及后验概率

图1给出了两种方法的预测结果。可以看出，本文所提方法的预测结果明显优于传统RVM的离线预测结果，并且随着时间推移，传统RVM的预测曲线偏离实际值曲线的幅度越来越大，而本文方法依然保持了较高的预测精度，这是由于随着时间的推移高压电源的状态也不断发生变化，传统RVM一成不变的预测模型已不能准确反映高压电源的变化情况，因此导致了预测精度逐渐下降，而本文方法通过不断更新模型参数来保持模型的动态预测能力，使得预测曲线更接近真实情况。表3给出了两种方法的数据对比，从20个样本均方根误差的对比可以看出，本文方法的预测误差仅为传统RVM离线预测误差的13.55%，预测精度大幅度高于传统RVM。在模型的训练时间上，虽然本文方法的总体训练时间长于传统RVM，但每次在线更新参数的平均训练时间为2.38 ms，仅为传统RVM训练时间的16.7%。

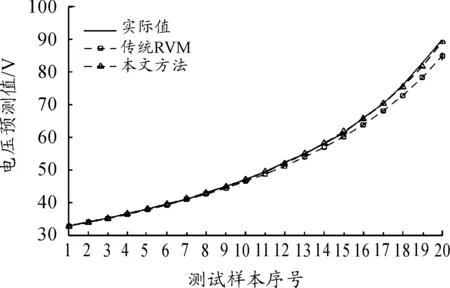
图1 预测结果

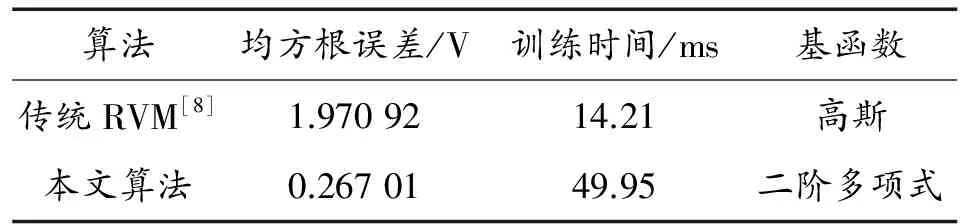
表3 两种方法的性能对比

5 实例预测实验

为验证所提方法在实际应用中的性能，本文以50倍音频放大器作为实验对象设计了实例预测实验，实验环境如图2所示。对于给定的激励信号，该音频放大器对其进行放大输出，示波器在固定时间间隔下采集并记录放大器的输出电压，温度传感器则监控实验过程中的设备温度，防止设备过热受损并分析温度对输出的影响。由于电子设备的可靠性较为稳定，在无退化情况下输出电压的变化范围十分微小，故本次实验以缓慢变化的正弦信号作为激励，模拟输出电压的漂移。实验中采样间隔取60 s，相空间重构的嵌入维数取5，实验过程共生成400组样本，将前100组作为离线样本对余下300个数据进行在线学习和预测，其他参数设置同第4节的仿真预测实验相同。

图2 实验环境

本文预测方法和传统RVM离线预测方法的预测曲线如图3所示，可以看出，在实际应用中由于各类噪声及测试设备误差的影响，输出信号存在一定的随机波动，输出电压的实际值并不是一条平滑的曲线，传统RVM的离线式预测随着时间的推移仍然存在着预测误差不断变大的现象，而本文提出的预测方法则保持了较高的预测精度，预测曲线更接近真实值。表4给出了两种方法的性能指标，在实际应用中，本文方法误差仅为传统RVM离线预测误差的30.64%，并且本文方法在线更新参数的平均训练时间仅为7.18 ms，大大小于传统RVM的离线训练时间。此外，本文方法自适应选择了二阶多项式核作为基函数，相比高斯核，二阶多项式核的局部学习能力较弱而全局学习能力更强，在本次实例预测实验中样本带有明显的噪声，高斯核较强的局部学习能力使得预测模型在训练时倾向于对噪声也进行解释，更容易产生过拟合现象，故本文自适应选择二阶多项式核作为基函数使得预测模型具有更好的鲁棒性。

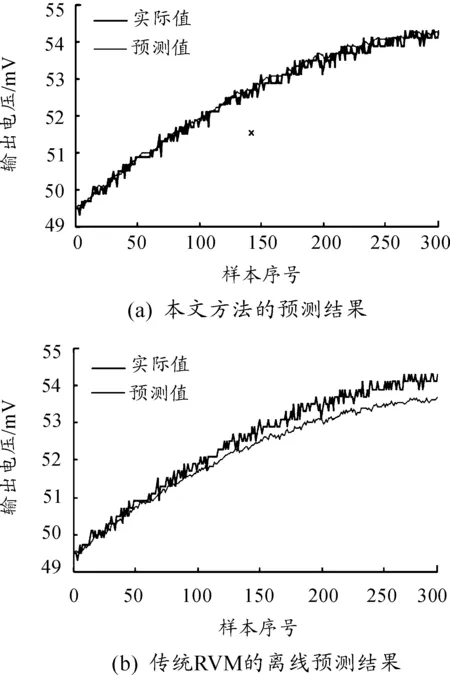
图3 预测结果

表4 两种方法的性能对比

6 结论

本文提出一种基于aRVM的电子设备在线状态预测方法，经仿真实验和实例实验验证表明：

1) 所提方法能够根据离线样本结构自适应选择最优基函数，提高预测模型对样本数据的表述能力；

2) 所提方法能够在新样本输入时快速实现模型参数的在线更新，使模型保持动态预测的能力，进一步提高整体预测精度；

3) 所提方法在实际应用中对噪声具有较好的鲁棒性，保持了较高的预测精度，具有一定的实际应用价值。

[1] 许丽佳.电子系统的故障预测与健康管理技术研究[D].成都：电子科技大学,2009.

[2] 刘震,王厚军,龙兵,等.一种基于加权隐马尔可夫的自回归状态预测模型[J].电子学报,2009,37(10):2113-2118.

[3] 赵建忠,欧阳中辉,张磊,等.基于多智能体遗传算法优化的航空电子设备状态组合预测[J].兵工学报,2016,37(4):727-734.

[4] 黄大荣,黄丽芬.灰色系统理论在故障预测中的应用现状及其发展趋势[J].火炮发射与控制学报,2009(3):88-92.

[5] 张弦,王宏力,张金生,等.状态时间序列预测的贝叶斯最小二乘支持向量机方法[J].西安交通大学学报,2010,44(10):42-46.

[6] 赵玉刚,鞠建波,张经伟.基于LIB-SVM的电子设备故障预测方法研究[J].计算机测量与控制,2015,23(6):1888-1891.

[7] 张弦,王宏力.局域极端学习机及其在状态在线监测中的应用[J].上海交通大学学报,2011,45(2):236-240.

[8] 范庚,马登武,张继军,等.基于自适应RVM的电子装备缓变故障预测方法[J].北京航空航天大学学报,2013,39(10):1319-1324.

[9] 汤巍,景博,黄以锋,等.振动载荷下面向电子设备PHM的板级封装潜在故障分析方法[J].电子学报,2016,44(4):944-951.

[10] 雷亚国,陈吴,李乃鹏,等.自适应多核组合相关向量机预测方法及其在机械设备剩余寿命预测中的应用[J].机械工程学报,2016,52(1):87-93.

[11] 张磊,李行善,于劲松,等.基于关联向量机回归的故障预测算法[J].系统工程与电子技术,2010,32(7):1540-1543.

[12] 黄帅栋,卫志农,高宗和,等.基于非负矩阵分解的相关向量机短期负荷预测模型[J].电力系统自动化,2012,36(11):62-66.

[13] TIPPING M E.Sparse bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001,1(3):211-244.

[14] TZIKAS D G,LIKAS A C,GALATSANOS N P.Sparse bayesian modeling with adaptive kernel learning[J].IEEE Transactions on Neural Networks,2009,20(6):926-37.

[15] TIPPING M E,FAUL A C.Fast Marginal Likelihood Maximisation for Sparse Bayesian Models[C]//International Workshop on Artificial Intelligence and Statistics,Key West,Florida,USA,2003:3-6.

[16] SCHMOLCK A,EVERSON R.Smooth relevance vector machine:a smoothness prior extension of the RVM[J].Machine Learning,2007,68(2):107-135(29).

[17] FAUL A C.Analysis of sparse bayesian learning[C]//Advances in Neural Information Processing Systems,Vancouver,British Columbia,Canada,2001:383-389.

[18] 汪洪桥,孙富春,蔡艳宁,等.多核学习方法[J].自动化学报,2010,36(8):1037-1050.

[19] 姚畅,陈后金,Yang,等.基于自适应核学习相关向量机的乳腺X线图像微钙化点簇处理方法研究[J].物理学报,2013,62(8):88702-088702.

[20] MACKAY D J C.Information theory,inference,and learning algorithms[J].Kybernetes,1972,50(10):640.

[21] TIPPING M E.Bayesian inference:an introduction to principles and practice in machine learning[J].Lecture Notes in Computer Science,2004,3176:41-62.

(责任编辑杨继森)

OnlineConditionPredictionofElectronicEquipmentBasedonRelevanceVectorMachinewithAdaptiveKernelLearning

GAO Mingzhe1， XU Aiqiang1， XU Qing2

(1.Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai 264001, China; 2.The No. 91635thTroop of PLA, Beijing 102200, China)

Aimed at the condition prediction of electronic equipment, an online prediction method based on relevance vector machine with adaptive kernel learning(aRVM) is proposed. In the proposed method, the condition prediction of electronic equipment is formulated as a supervised-learning problem. Firstly, the basis function which is most suitable for prediction problem is selected according to the posterior probability of equipment offline data. Then the prediction model based on aRVM is trained by offline data. Finally, the parameters of the model are updated dynamically through incremental training of online samples in the prediction process. Experimental results of both simulation experiment and practical experiment indicate that the proposed method obviously outperforms the traditional one in both prediction accuracy and online training efficiency.

electronic equipment; status prediction; relevance vector machine; online training; adaptive kernel

2017-07-25；

2017-08-30

装备预研基金资助项目(9140A27020214JB14435)

高明哲(1988—)，男，博士研究生，主要从事电子装备的测试与故障诊断技术研究。

10.11809/scbgxb2017.11.024

本文引用格式：高明哲,许爱强，许晴.基于aRVM的电子设备状态在线预测方法[J].兵器装备工程学报，2017(11):108-113.

formatGAO Mingzhe，XU Aiqiang，XU Qing.Online Condition Prediction of Electronic Equipment Based on Relevance Vector Machine with Adaptive Kernel Learning[J].Journal of Ordnance Equipment Engineering,2017(11):108-113.

TP206

A

2096-2304(2017)11-0108-06