卸压巷对被保护巷变形影响的数值模拟*

易 帅,唐 海,王建龙,丁安松,吴仕鹏

(湖南科技大学 资源环境与安全工程学院, 湖南 湘潭市 411201)

卸压巷对被保护巷变形影响的数值模拟*

易 帅,唐 海,王建龙,丁安松,吴仕鹏

(湖南科技大学 资源环境与安全工程学院, 湖南 湘潭市 411201)

在矿业开采过程中，巷道围岩受应力变化影响，顶底板与两帮均会发生变形收敛。通过开挖卸压巷和优化卸压巷的几何参数，能有效减少巷道围岩收敛。利用3DEC离散元模拟软件，模拟在400 m埋深条件下不同形状、位置的卸压巷对被保护巷道的顶底板、两帮的位移变化规律，研究卸压巷对被保护巷道的影响。模拟结果表明：以X正方向为起点0°，逆时针旋转，在离被保护巷1.65倍巷宽的315°位置处，开挖正(长)方形卸压巷，能有效减少被保护巷的整体变形。

卸压巷；巷道变形； 数值模拟；离散元

伴随着我国煤矿开采技术的飞速发展，以及煤矿深度的逐渐加深、条件愈趋恶劣，巷道支护由此越加困难[1￣2]。目前认为，锚杆支护是一种经济、有效的巷道支护手段[3￣4]。但是锚杆支护并非是唯一的解决手段，研究表明，通过合理的卸压巷技术，给巷道一个良好的低应力环境，降低支护难度，一定程度上也能增加巷道支护有效作用[5]。

一直以来，国内外的学者开展了很多关于巷道卸压方面的研究，伴随着数值模拟技术的发展，以数值模拟为手段分析卸压巷机理与几何特征的研究逐渐增多。张伟杰、兰思栋[6]采用数值模拟的研究手段，分析了卸压巷与巷道开挖顺序、巷道位置及巷道尺寸对卸压效果的影响。段军、杨鹏等人[7]结合工程实践与数值模拟，分析了沿空巷道围岩垂直应力分布规律，以及不同位置下卸压巷对沿空掘巷围岩应力分布的影响。何荣兴、任凤玉等人[8]利用数值模拟的方法，研究了不同卸压巷高度和宽度下采场进路应力分布状态。苏海、赵玉成等人[9]基于ANSYS 数值模拟软件，研究了卸压巷位置、尺寸对下部巷道两帮移近量和底鼓量的规律。

综上所述，采用数值模拟手段分析卸压巷力学机理，已经是目前研究领域比较成熟、有效的研究手段。而以往的研究多采用有限元、有限差分等数值模型，缺乏对岩体本身不连续性的考虑。因此，本文在唐海、吴仕鹏、赵海龙[10]的研究基础上，基于3DEC离散元模拟软件，建立巷道岩体不连续模型，研究卸压巷位置、形状、中心距对煤矿中央水泵房变形的影响，为卸压巷的研究、实践提供一定的理论基础。

1 卸压巷的卸压机理

卸压巷可以通过降低被保护巷所处的应力，提高巷道稳定性，减少变形。为简单起见，本文选取圆形巷应力-应变曲线作为例证分析。如图1所示，在被保护巷上方开挖卸压巷，使重力场的应力分布状态发生变化，形成应力增高区与应力降低区，再通过优化卸压巷几何参数，使被保护巷处于应力降低区，可以有效提高巷道稳定性。

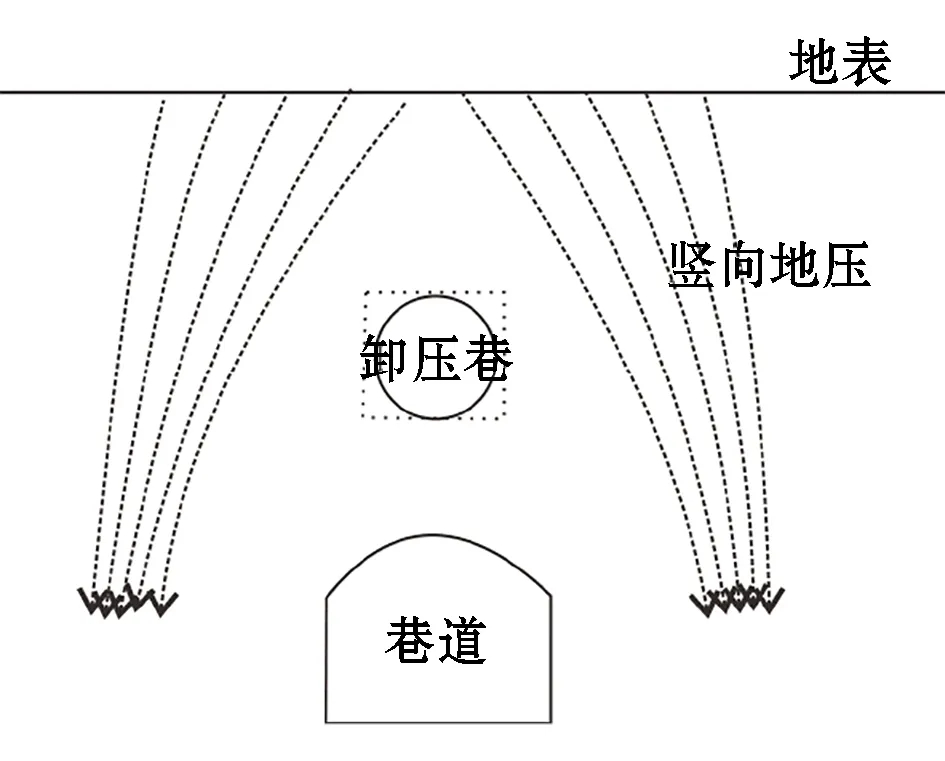
图1 卸压巷机理

一般研究认为，圆形卸压巷道直径的确定可根据d2=SW/2计算[11]，其中S为工程巷道的面积，W为无卸压巷时巷道断面收缩率，一般为50%。工程实践及已有研究表明，合理的设计卸压巷位置、卸压巷与被保护巷道的中心距，一定程度上能优化卸压巷对被保护巷道的卸压效果。另一方面，不同形状的卸压巷所表现的应力分布不同，合理的选择卸压巷的形状参数，也能有效的优化卸压效果。

2 数值模拟

2.1 地质状况

模拟煤矿其煤层平均埋深H为400 m，煤厚2.1～6.2 m，平均厚度3.1 m，倾角0°～8.4°，平均倾角5.2°，属近水平煤层，模拟巷道位于煤层及石灰石中。主要地层力学参数见表1[10]。

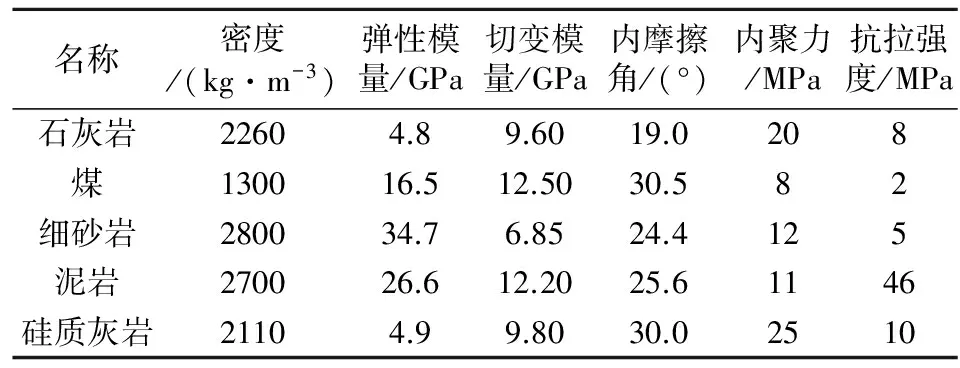
表1 主要地层力学参数

2.2 数值模型

选用3DEC离散元软件，根据地质环境建立尺寸为60 m ×30 m ×60 m的力学模型(如图2所示)，中央水泵房截面为宽6 m、直墙高3 m、半径为3 m的半圆拱型巷，主要地层为煤、石灰岩。模型边界条件4个侧面为水平位移约束，底面为竖向位移约束，顶面为应力边界，应力大小等同模型上边界以上的上覆岩层自重，计算为上覆岩层容重γ与上覆岩层厚度H之积(σ=γH)，模型的本构模型采用莫尔-库伦模型。图3为被保护巷(中央水泵房)监测点布置图。

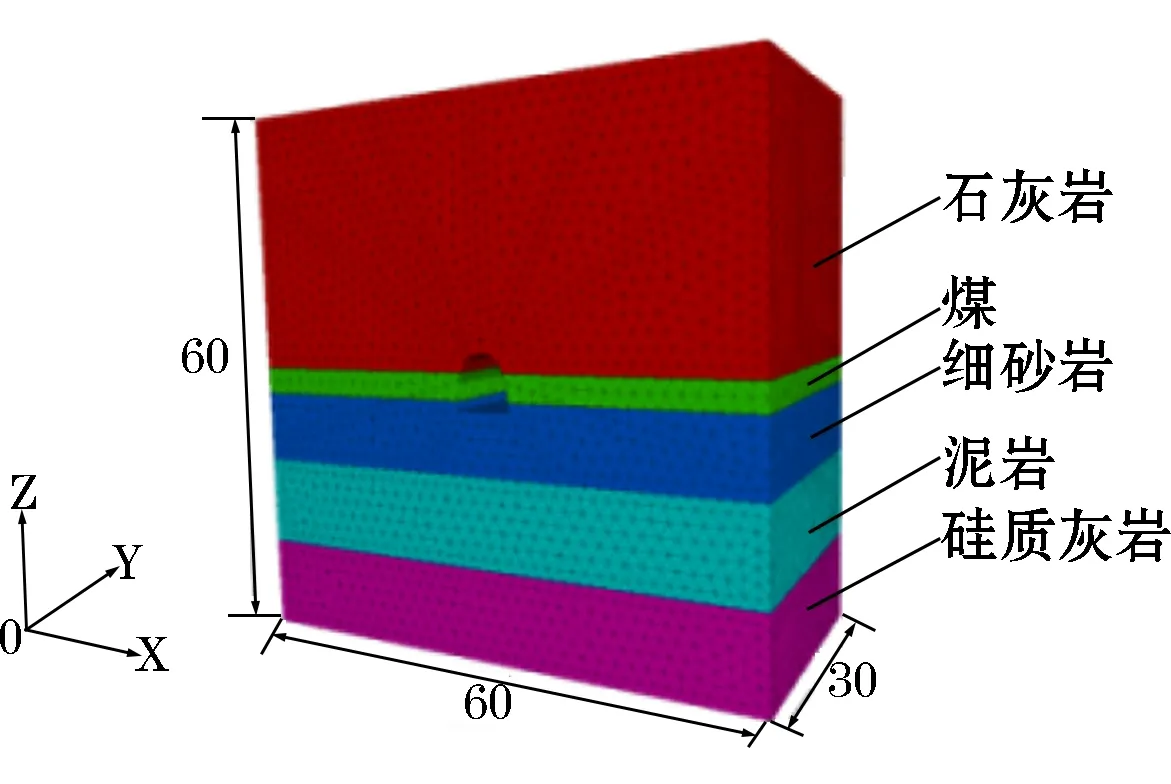
图2 中央水泵房力学计算模型

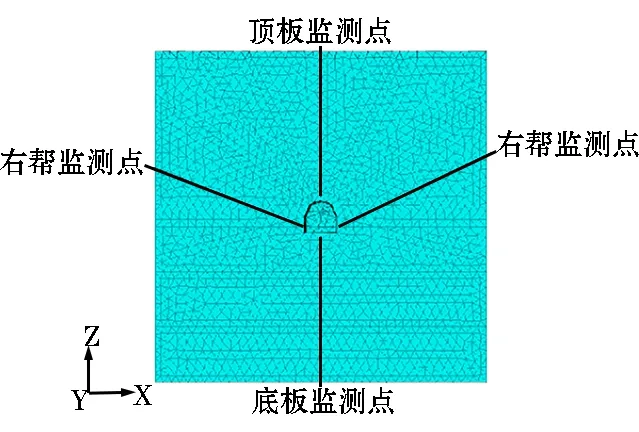
图3 被保护巷(中央水泵房)监测点布置图

本文主要模拟研究卸压巷位置、中心距、形状对被保护巷的卸压效果，为提高准确性，在研究单一影响因素时，设置一致的卸压巷、被保护巷背景参数，模拟全部选择超前开挖方式，且卸压巷长度与被保护巷长度一致。根据公式d2=SW/2 计算得d=2.78 m，实际取值范围3～4 m，模拟选择d=3.5 m。模拟方案如下：

(1) 卸压巷位置因素影响的模拟方案设计为:以模型X轴正方向为起点、间隔45°，逆时针方向布置8种卸压巷。

(2) 卸压巷与被保护巷中心距因素影响的模拟方案设计为:中心距为1， 1.5， 2， 2.5， 3倍被保护巷宽的卸压巷。卸压巷位置根据模拟方案1的结果选择。

(3) 卸压巷形状因素影响的模拟方案设计为:圆形、正方形、长方形与半圆拱形卸压巷，且各卸压巷面积相近。卸压巷位置、中心距根据模拟方案1，2的结果选择。

3 巷道变形分析

为了研究不同卸压巷对被保护巷变形的影响，本模拟通过对比开挖卸压巷前后的位移，确定卸压巷对被保护巷的变形影响；对比卸压后位移变化率(式(1))，判断最优卸压巷参数。模拟选择被保护巷顶板、两帮、底板四个监测点做数据统计与简要分析。表2为无卸压巷时监测点位移，其中左右两帮位移绝对值不一样，在苏海等人[9]的卸压巷研究中，亦同样出现此类现象，具体原因有待进一步研究。

位移变化率W为：

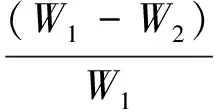
(1)

式中，W1为无卸压巷时被保护巷的位移;W2为卸压巷下被保护巷的位移。由式(1)可知，当位移变化率为正时，代表卸压巷下被保护巷监测点位移减少；当位移变化率为负时，代表卸压巷下被保护巷监测点位移增加。

表2 无卸压巷时监测点位移

注：顶底板位移正值代表Z轴正方向；左右帮位移正

值代表X轴正方向。

3.1 不同位置卸压巷对巷道变形的影响

表3为有卸压巷时监测点位移，图4为不同位置卸压巷监测点位移变化率曲线，由式(1)计算而得。

根据表2、3及图4可知：在被保护巷270°位置开挖卸压巷，顶板位移减少率为7.22%左右，卸压巷对顶板变形的抑制效果最好；在被保护巷90°位置开挖卸压巷，底板位移减少率为12.49%左右，卸压巷对底板变形的抑制效果最好；在被保护巷225°位置开挖卸压巷，左帮位移减少率为43.07%左右，卸压巷对左帮变形的抑制效果最好；在被保护巷135°位置开挖卸压巷，右帮位移减少率为9.75%左右，卸压巷对右帮变形的抑制效果最好。同时，由图4可知，部分位置开挖卸压巷时，会加剧被保护巷某侧位移。例如90°、270°位置卸压巷开挖后，被保护巷两帮位移明显增加。由此，综合分析可知：本模拟中卸压巷开挖在被保护巷315°位置，被保护巷整体位移最小；45°、135°、225°位置开挖卸压巷整体位移较小；90°、270°位置卸压巷其次；0°、180°位置卸压巷最差。

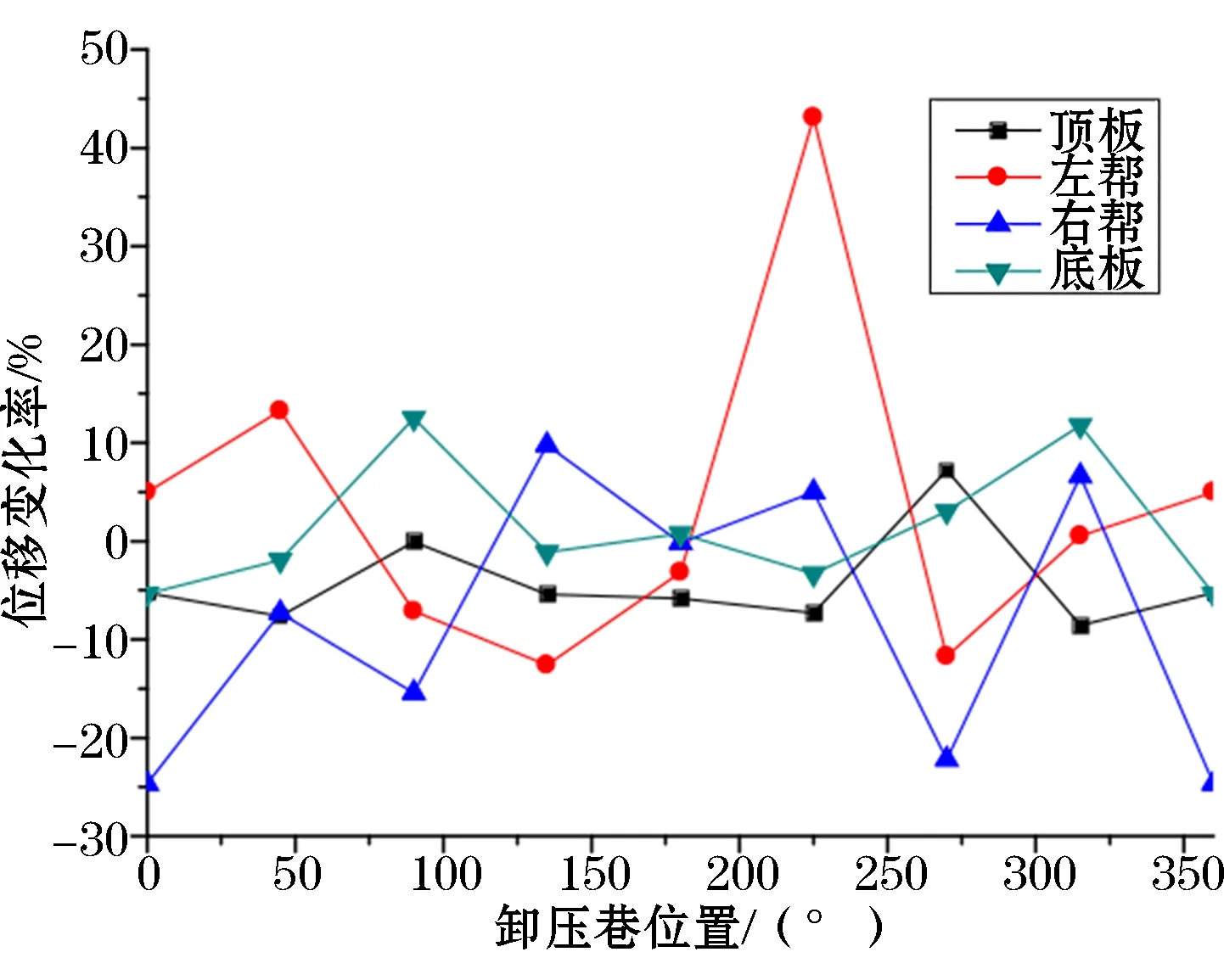
图4 不同位置卸压巷监测点位移变化率曲线

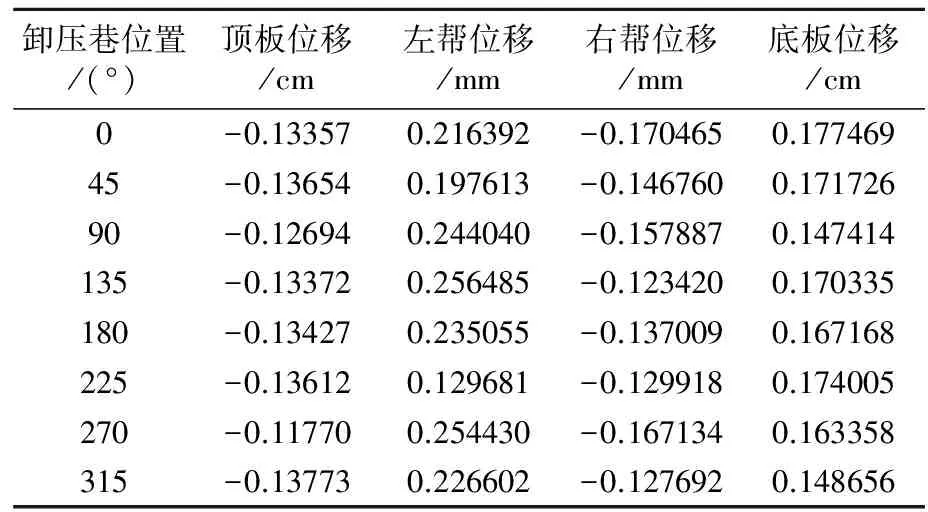
卸压巷位置/(°)顶板位移/cm左帮位移/mm右帮位移/mm底板位移/cm0-0．133570．216392-0．1704650．17746945-0．136540．197613-0．1467600．17172690-0．126940．244040-0．1578870．147414135-0．133720．256485-0．1234200．170335180-0．134270．235055-0．1370090．167168225-0．136120．129681-0．1299180．174005270-0．117700．254430-0．1671340．163358315-0．137730．226602-0．1276920．148656

注：顶底板位移正值代表Z轴正方向；左右帮位移正值代表X轴正方向。

3.2 不同中心距卸压巷对巷道变形的影响

根据上述结果，315°位置卸压巷被保护巷整体位移最小。因此，本阶段模拟选择315°位置卸压巷，其他条件不变。图5为不同中心距卸压巷监测点位移变化率曲线。

根据图5可知，卸压巷下被保护巷顶板位移变化率为负值，表明目前条件下顶板位移加剧；卸压巷与保护巷距离(中心距)在2.5倍巷宽附近，卸压巷能有效减小被保护巷左帮位移；卸压巷与保护巷距离(中心距)在1.5～2.5倍巷宽，卸压巷能有效减小被保护巷右帮位移；卸压巷与保护巷距离(中心距)在1.5倍巷宽附近，卸压巷能有效减小被保护巷底板位移。同时，模拟中依旧存在加剧被保护巷某侧位移的情况，但程度明显降低。由此，综合分析可知：卸压巷与保护巷距离(中心距)在1.5～2.5倍巷宽时，可以有效减小被保护巷整体位移。

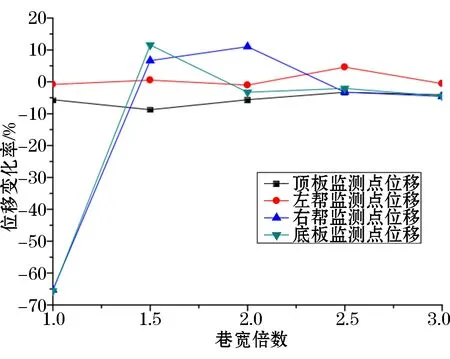
图5 不同中心距卸压巷监测点位移变化率曲线

3.3 不同形状卸压巷对巷道变形的影响

根据上述数据，本阶段模拟中心距为10 m(1.65倍巷宽)，其他条件不变。图6为不同形状卸压巷监测点位移变化率点状图。

根据图6分析可知：圆形、半圆拱形卸压巷下，被保护巷道右帮位移分别减少了41.8%、27.3%，但加剧了被保护巷其他侧位移，被保护巷道顶板位移分别增加了4.8%、7.9%，被保护巷道左帮板位移分别增加了2.6%、3.6%，被保护巷道底板位移分别增加了1.5%、21.7%；正方形卸压巷下被保护巷道除顶板、左帮位移基本不变，右帮位移减少19.9%，底板位移减少8.3%；长方形卸压巷下被保护巷道除顶板、底板位移基本不变，左帮位移减少3.5%，右帮位移减少31.6%。

3.4 卸压巷对被保护巷变形的影响

综上所述，开挖卸压巷对于被保护巷的顶底板、两帮变形抑制效果有明显差异。不同几何参数下的卸压巷，在减少被保护巷某侧变形的同时，还会加剧被保护巷其他侧变形。根据本文数值模拟，通过优化卸压巷形状、中心距与位置参数，最终确定在离被保护巷1.65倍巷宽的315°位置处，开挖正(长)方形卸压巷，能有效减少被保护巷整体变形。参考数值模拟下卸压巷的优化参数，在中央水泵房附近开掘卸压巷，并设计锚杆支护系统支护被保护巷。目前，经现场实测发现，中央水泵房变形微小，巷道稳定。

综合分析卸压巷对整个被保护巷顶底板、两帮的卸压效果，是施工设计过程中需要考虑的重要因素。通过合理规划卸压巷的位置、形状、中心距等参数，可以用于减少被保护巷的整体变形，也可以针对顶底板、两帮某侧变形，配合锚杆等手段对巷道某侧支护。

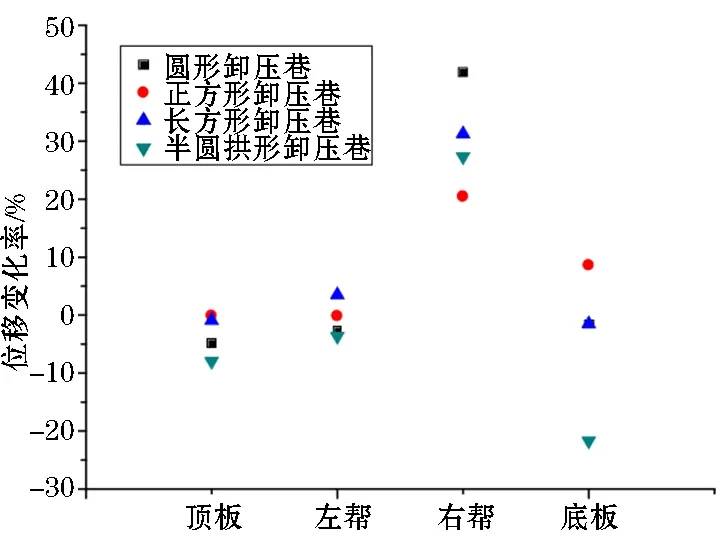
图6 不同形状卸压巷监测点位移变化率点状图

4 结 论

(1) 卸压巷开挖在被保护巷315°位置，被保护巷整体位移最小，45°、135°、225°位置开挖卸压巷位移较小，90°、270°位置其次，0°、180°位置较差。

(2) 卸压巷与保护巷距离(中心距)在1.5～2.5倍巷宽时，可以有效减小被保护巷位移。

(3) 正、长方形卸压巷对减少被保护巷变形效果较好；圆、半圆拱形卸压巷有加剧被保护巷其他侧变形。

(4) 卸压巷在减少被保护巷某侧变形时，可能会增加其他侧变形。合理规划卸压巷的几何参数，即可以用于减少被保护巷的整体变形，也可以针对顶底板、两帮某侧变形，再辅以支护，增强被保护巷整体稳定。

[1]蓝 航,陈东科,毛德兵.我国煤矿深部开采现状及灾害防治分析[J].煤炭科学技术,2016,44(1):39￣46. [2]王建建.袁庄矿回采巷道卸压槽技术研究及应用[D].合肥：安徽理工大学,2016.

[3]康红普,王金华.煤巷锚杆支护理论与成套技术[M].北京:煤炭工业出版社,2007．[4]侯朝炯,郭励生,勾攀峰,等.煤巷锚杆支护[M].徐州:中国矿业大学出版社,1999．[5]李俊平,连明杰.矿山岩石力学[M].北京:冶金工业出版社,2013.

[6]张伟杰,兰思栋.高应力下卸压巷道围岩破坏机理及卸压过程数值分析[J].矿冶工程,2014,34(4):34￣38.

[7]段 军,杨 鹏,蔡志炯,等.金庄矿特厚煤层综放沿空巷道围岩卸压控制研究[J].煤炭技术,2016,35(02):21￣23.

[8]何荣兴,任凤玉,丁航行,等.巷道卸压法应力迁变规律及卸压参数的确定[J].东北大学学报(自然科学版),2015,36(10):1457￣1460.

[9]苏 海,赵玉成,刘家成,等.卸压巷道位置和尺寸对下部巷道底鼓影响规律研究[J].煤炭技术,2015,34(2):53￣55.

[10]吴仕鹏,唐 海,赵海龙.充填步距和推进距离对基本顶下沉影响的数值模拟[J].中州煤炭,2015,12:54￣58.

[11]鲁 岩,邹喜正,刘长友.巷旁开掘卸压巷技术研究与应用[J].采矿与安全工程学报,2006,23(3):329￣336.(收稿日期：2017￣06￣17)

国家自然科学基金资助项目(51374104).

易 帅(1993-), 男，湖北潜江人，研究生，研究方向为采矿与岩石力学,Email：929755790@qq.com。