一种基于混沌映射的快速图像加密算法
杨晓刚
(西安交通大学 西安 710061)
信号/数据处理
一种基于混沌映射的快速图像加密算法
杨晓刚
(西安交通大学 西安 710061)
为了有效解决图像加密算法存在的复杂度高、安全性差等问题,提出了一种基于混沌映射的快速图像加密算法。该算法运用两种不同的混沌映射,结合明文图像本身特征,快速地实现了对明文图像的安全加密。仿真实验表明:无论是灰度图像还是彩色图像,文中提出的图像加密算法,均能满足速度快、效果好的加密要求,特别是大批量图像的加密任务。对于一副256*256的Lena图像来说,加密时间仅0.057s,解密时间0.060s。
混沌映射;图像加密
0 引 言
近年来,随着互联网和多媒体技术的快速发展,数字图像已成为主要的网络交互对象之一[1]。今天,当成千上万的数字图像在网络上进行传输时,就时刻面临着被非法截获、破译、转载等现实威胁。因此,图像信息的安全性和保密性要求,就成为信息安全领域的一个重要研究方向[2]。
目前,科研人员已经在该领域取得了许多成果[3-5],设计出众多的图像加密算法。其中,基于混沌映射的图像加密算法有很多,如文献[6]、文献[7]中所提到的基于二维或三维的Logistic混沌映射图像加密算法,文献[8]、文献[9]中提到的基于超混沌系统的数字图像加密算法等,还有基于图像压缩、数字矩阵、频域变换及DNA计算等技术的图像加密算法,但大多存在一定的安全风险[10],且部分算法仅能对彩色或灰度图像中的某一种进行加密,受图像本身的尺寸特征影响较大,适用性和时效性上还有较大差距。算法种类虽多,但基于混沌系统的加密算法因混沌系统自身所具有的遍历性、对初始值极端敏感性等特点而被广泛应用于数字图像加密领域,并逐渐成为图像加密领域研究的热点。
为了主动克服低维混沌系统存在的参数和初始值个数少,密钥空间较小,算法的安全性较低及混沌序列随机性较差[11]等困难,充分发挥低维混沌系统结构简单、效率更高的优势,本文提出了一种基于混沌系统的快速图像加密算法,该算法不受图像类型、尺寸影响,均能实施安全、高效的加密操作,有很强的实际应用价值。实验结果表明,该算法实现简单,运行高效,能充分保证数字图像的安全性。
1 混沌系统
1.1 混沌映射
为了提高数字图像加密算法的安全性,本文采用了如下两种混沌系统:
(1)二维Logistic混沌映射
二维Logistic混沌映射定义如公式(1)所示,其中初值和参数的设置为μ=4,β=0.1,α1=α2∈[0.65,09],系统进入混沌状态 。
(1)
(2)三维Lorenz混沌映射
Lorenz系统是经典的三维混沌系统,其具有系统复杂,混沌序列多维等优点,便于算法设计,灵活处理。其定义如公式(2)所示。其中,β,δ,ρ为系统参数,当β=8/3,δ=10,ρ=28,在保持β,δ不变,ρgt;24.74时Lorenz系统进入混沌状态[12]。
(2)
2 加密算法设计
假设原始图像I的大小为m*n(M=m*n),则加密算法的具体步骤如下:
(1)根据加密密钥,生成三维Lorenz混沌映射的初始值x10,y10,z10及ρ值。其中,密钥是由64个十六进制数字组成的256位的字符流,具体情况如表1所示。
(2)根据三维Lorenz混沌映射的初始值x10,y10,z10、 系统参数ρ及迭代次数T产生三维混沌序列X、Y、Z。
(3)从混沌序列X中抽取长度为m的子序列X1。
(4)对长度为m的子序列按公式(3)进行重新赋值计算。
X2(i)=round(X1(T-m+i)/(m-1))+1
(3)
(5)从混沌序列Y中抽取长度为n的子序列Y1。
(6)对长度为n的子序列按公式(4)进行重新赋值计算。
Y2(i)=round(Y1(T-n+i)/(n-1))+1
(4)
(7)分别对第(4)步和第(6)步产生的子序列X2和Y2进行优化处理,得到新的序列X2*和Y2*。具体方法:查找序列中是否有相同数值的元素,如有,则按其出现的位置和数值大小,对其进行替换操作,直至序列中没有相同数值的元素,达到对序列进行优化处理的目的。
(8)利用加密密钥,生成二维Logistic混沌映射的初始值x20,y20及α1α2值。
(9)根据二维Logistic混沌映射的初始值x20,y20、系统参数α1,α2及迭代次数R产生二维混沌序列XX、YY。
(10)按公式(5)构建控制参数P,其中i∈(0,49),P(0)=0。
P(i+1)=P(i)+XX(R-i)
(5)
(11)按公式(6)构建控制参数S,其中i∈(t,R-c)。其中,t和c是可变参数。S(t)=0,YY(i)为二维混沌序列中的值。
S(i+1)=S(i)+YY(i)
(6)
(11)按公式(7)~(9)构建出控制参数Q、W和U。
Q=(S(R-c+1)+P(50))mod1
(7)
W=1+round(Q*253)
(8)
U=W/255
(9)
(12)根据公式(10)对三维Lorenz混沌映射所产生的Z序列进行赋值计算,得到序列Z1。其中,i∈(1,T)。
Z1(i)=((Z(i)/1000)+U)mod1
(10)
(13)根据公式(11)计算出E(i,j),并将其转换为数字图像,即为第一次加密。其中,i∈(1,m),j∈(1,n)。
E(i,j)=(I(X2*(i),Y2*(j))
+Z1((i*jmodT)+1)) mod 1
(11)
(14)根据公式(12)对(13)步的加密结果进行第二次加密。其中,H(1)=E(1)⊕c。
H(i+1)=H(i) ⊕Z⊕E(i+1)
(12)
(15)将(14)步所得结果转换为M*N的图像矩阵,即为加密结果。
加密算法的流程图如图1所示:
表1 密钥定义

密钥控制参数初始值64个十六进制数D1,D2,…D64D∈[0~9,A~F]参数计算A=(D1,D2,…D8)10/(264+1)B=(D9,D10,…D16)10/(264+1)C=(D17,D18,…D24)10/(264+1)D=(D25,D26,…D32)10/(264+1)E=(D33,D34,…D40)10/(264+1)F=(D41,D42,…D48)10/(264+1)G=(D49,D50,…D56)10/(264+1)H=(D57,D58,…D64)10/(264+1)Lorenz混沌β=24.86+((E+F+U)mod1)*0.001X10=(H+F+U)mod1y10=(F+G)mod1z10=(H+E+U)mod1Logistic混沌α1=α2=0.888+((A+C)mod1)*0.001X20=(A+B)mod1Y20=(C+D)mod1
3 实验结果及安全性分析
算法的实现平台:基于Matlab R2012a软件平台,硬件配置为Intel(R) Core(TM) i3-3220 CPU@3.30GHz,可用内存3.88GB,64位windows 8.1中文版操作系统。
3.1 统计直方图分析
直方图是描述图像像素值空间分布规律的一种数据形式。图2、图3给出了明文图像和密文图像的统计直方图。从图2可以看出,明文图像直方图呈高低起伏态势,分布极不均匀,反映出直方图信息的分布与图像本身内容有着密切的联系,且图像本身的内容主要集中在某一区域内。而加密后的图3明显可以看出,直方图信息空间分布比较均匀一致,反映不出与该图像本身内容之间的任何联系,符合随机噪音图像的基本特性,很好地扰乱了原始图像信息,起到了加密的效果,可以有效抵抗已知明文或选择明文攻击。
3.2 相邻像素相关性分析
对于任意一幅明文图像来说,相邻像素点的灰度值往往比较接近,反映出它们之间存在着很大的相关性。这种相关性关系既可以用图表现出来,也可以用数值来衡量,其值为-1到1之间的小数,0
表示毫不相关。文中我们分别从原始图像和加密图像中随机选取N(N=1000)对相邻的像素点,分别测试其水平方向、垂直方向和对角线方向的像素相关性。运用Matlab平台,绘出256*256的Lena图像中所选各点的空间位置分布图,如图4所示。
从图4中可以看出,明文图像无论是水平方向,还是垂直方向或对角线方向上相邻像素几乎分布在一条直线上。而密文图像在3个方向上的相邻像素点杂乱地分布于整个像素空间,无明显规律可循。对于图像相邻像素之间的这种相关性我们也可能通过公式(12)~(15)来进行分析。计算相邻像素点的相关系数公式如下:
(12)
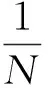
(13)
(14)
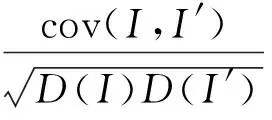
(15)
表1 图像加密前后相邻像素相关性对比
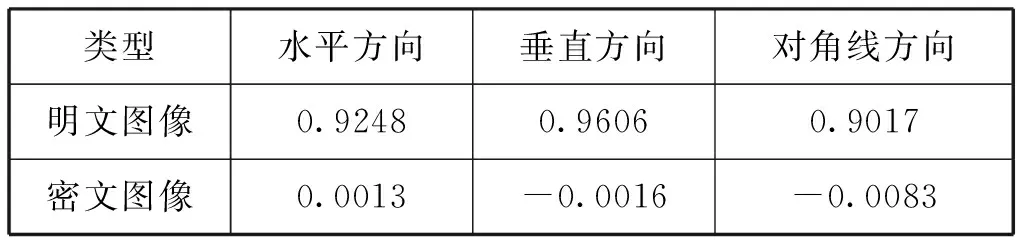
类型水平方向垂直方向对角线方向明文图像0.92480.96060.9017密文图像0.0013-0.0016-0.0083
3.3 信息熵
在图像处理领域用来反映图像中所包含信息的不确定性,称为图像的信息熵。一个信源的信息熵计算公式如下:
(16)
式中,p(mi)为信号mi的概率,L为每个信号的比特数。从理论上讲,理想情况下密文图像的信息熵应该为8。经实验测试,图像Lena的信息熵分别为7.9951,值非常接近理想值,反映出该算法可以很好地抵御外来熵攻击。
3.4 敏感性分析
敏感性分析主要考察的是对密钥的敏感性和对明文图像的敏感性。当密钥或明文发生变化时,两幅图像之间的平均差异强度,即一致平均变化强度(UACI)。而CPCR是指当密钥或明文发生变化时,两次加密所得之间的像素变化率。其计算公式分别如下[5]:
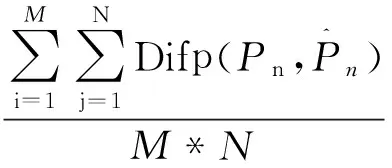
(17)
(18)
(19)
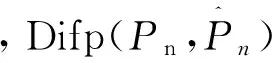
表2 算法对密钥的敏感性测试

算法NPCR/%UACI/%文中算法99.6133.36
接着,测试一下算法对明文的敏感性。结果如表3所示:
表3 算法对明文的敏感性测试

算法NPCR/%UACI/%文中算法99.5333.75
3.4 密钥空间分析
本文采用64个十六进制数构成的256位字符串,通过它们之间的混合运算,将其结果作为映射的状态初值,至于迭代次数、计算步长及可变参数t和c均可作为控制参数,使密钥空间大大扩展,故文中算法具有抗穷举攻击的能力。
4 结语语
本文基于三维Lorenz系统和二维的Logistic系统提出了一种基于混沌系统的快速图像加密算法,并从直方图、相邻像素相关性、信息熵等方面对算法进行了安全性分析。实验表明:该算法具有密钥空间大、加密对象灵活、速度快、抗攻击能力强等多种优势,特别是对统计分析攻击、已知或选择明文攻击均具有良好的安全性。
[1] 张晓强,王蒙蒙,朱贵良.图像加密算法研究新进展[J].计算机工程与科学,2012,34(5):1-6.
[2] 任洪娥,戴琳琳,张健.基于混沌数列变换的图像加密算法[J].计算机工程与设计,2013,34(5):1615-1619.
[3] 许艳.基于Logistic映射的BMP图像加密算法[J].现代计算机,2009,26(2):80-82.
[4] 潘勃,冯金福,陶茜,等.基于超混沌映射和加法模运算的图像保密通信方案[J].计算机科学: 2009,36(8):273-275.
[5] 李波.可变区间混沌映射在图像加密中的应用研究[J].计算机工程及设计: 2010,31(24):5176-5178.
[6] 周蕊,于晓明,焦占亚.一种基于混沌序列的数字图像加密算法[J].微电子学与计算机: 2010,27(12):62-68.
[7] 罗玉玲,杜明辉.基于量子Logistic映射的小波域图像加密算法[J].华南理工大学学报:自然科学版,2013,41(6):0053-0062.
[8] 许慧雅,廖利.基于超级混沌系统的图像加密算法[J].激光杂志:2015,36(4):79-81,85.
[9] 章秀君,吴志强,方正.一种基于四维超混沌系统的数字图像加密算法[J].计算机工程: 2013,39(8):169-172.
[10] S.Zhou, Q.Zhang, X.Wei, etc. A summarization of image encryption, IETE Tech. Rev. 2010, 27(6):503-510.
[11] Sun Fuyan, Liu Shutang, Li Zhongqin, et al.A Novel Image Encryption Scheme Based on Spatial Chaos Map[J].Chaos,Solitons amp; Fractals,2008,38(3):631-640.
[12] 王东生,曹磊.混沌、分形及其应用[M].合肥:中国科学技术大学出版社,1995.
AFastImageEncryptionAlgorithmBasedonChaoticMapping
Yang Xiaogang
(Xi’an Jiaotong University, Xi’an 710061)
In order to effectively solve problem of image encryption algorithm, including high complexity and poor security, a fast image encryption algorithm based on chaotic mapping is presented. The algorithm can quickly implement plain image encryption by using two different chaotic mappings and combining with feature of plain image itself. Simulation experiments show that the proposed image encryption algorithm can meet high speed and good encryption requirement to both color or gray image, it is especially suitable for encryption of large quantity images. To a Lena image with size of 256*256, encryption time is only 0.057s, decryption time is 0.060s.
chaotic mapping; image encryption
2017-08-20
陕西省自然科学基金 (2015JM8322)
杨晓刚(1981-),男,硕士研究生。研究方向为信息安全技术。
TP309
A
1008-8652(2017)03-034-05

