基于二元分布估计算法的置换流水车间调度方法

裴小兵 赵 衡

天津理工大学管理学院，天津，300384

基于二元分布估计算法的置换流水车间调度方法

裴小兵 赵 衡

天津理工大学管理学院，天津，300384

针对最大完工时间最小的置换流水车间调度问题，提出了一种结合二元分布估计算法与生物地理学算法的混合优化算法(HB-EDA)。算法以分布估计算法为架构，以二元概率模型为进化依据，针对优秀染色体和劣势染色体分别通过概率模型挖掘出具有优势信息和劣势信息的链接基因区块组成区块库1和区块库2，借鉴生物地理学算法中的群体迁移思想，用两个区块库分别对优势和劣势染色体以指定比例进行更新操作产生子群体，并对染色体进行切段与重组，以进一步筛选高适应度的解。最后通过对Reeves和Taillard标准测试集的仿真结果和算法比较验证了所提出算法的有效性。

置换流水车间调度；生物地理学优化算法；分布估计算法；组合区块

0 引言

作为一种典型的组合优化问题(combinatorial optimization problem, COP)，置换流水车间调度问题(permutation flow-shop scheduling problem, PFSP)受到国内外学者的广泛研究，并被证

明是NP困难问题[1]。针对置换流水车间调度问题的求解方法大致可分为精确算法、启发式算法、元启发式算法三种类型。精确算法主要有分支定界法、数学规划法(线性规划、整数规划、动态规划等)方法[2]，可以求得问题的精确解，由于NP困难问题的复杂性，精确算法难以在有限时间内求得确定解，故只适用于小规模问题。启发式算法主要有NEH(Nawaz-Enscore-Ham)算法、Plamer法、Gupta法等，虽然能在较短时间内构造解，但难以保证质量。元启发式算法主要有遗传算法、模拟退火算法、禁忌搜索算法、粒子群算法、蚁群算法等，文献[3-4]对启发式和元启发式算法求解PFSP问题作了比较和评价。

分布估计算法(estimation of distribution algorithms, EDA)是一种基于统计学习的优化算法，近年来得到广泛的研究和发展，目前EDA算法已在工程优化、机器学习、模式识别等多个问题上得到应用[5-6]。遗传算法根据达尔文进化论的优胜劣汰规则，通过染色体交叉、变异、重组等方式搜寻解空间找寻最优解，但由于优秀解通常具有相似的序列结构[7]，进化后期难以通过交叉变异等操作获得新的性状，易陷入局部最优，导致演化机制耗费大量时间做重复且无效的工作。而EDA算法利用概率模型生成子代，通过学习与挖掘取代交叉与突变两大自然机制[8]。为获得更好的求解能力，国内外学者将EDA算法与元启发式算法或局部搜索机制相结合构建混合型算法。LIU等[9]将粒子群算法与EDA算法结合，通过搜索机制混合操作确保了粒子群体与局部最优机制信息共享，增强了原始粒子的搜索能力。TZENG等[10]提出了一种将EDA算法与蚁群算法(ACS)混合的算法，使用局部最优解产生概率模型，并使用ACS算法解构造方法产生子代，用于求解PFSP问题。ROBLES等[11]基于遗传算法(GA)和分布估计算法提出了一种GA-EDA算法，使用GA算法和EDA算法两种机制产生群体，取较好的组成初始解。叶宝林等[12]将EDA算法与一种混合邻域搜索机制结合，构建了一种两阶段PFSP算法。孙良旭等[13]针对PFSP问题提出一种两阶段分布估计算法，先利用NEH算法启发式构造较优初始个体，使用概率模型产生下一代种群。何小娟等[14]基于EDA算法构建出工件排列顺序和工件频率两个概率模型，并使用Bayesian公式建立一个后验概率模型，以更好地指导新群体的产生。

生物地理学优化算法[15](biogeography-based optimization，BBO)是近年来兴起的一种基于群体计算的全局进化算法，目前已在基准测试函数和优化问题上表现出良好的性能，但应用于PFSP问题尚属首次[16]。从目前文献看，EDA算法在求解车间调度问题上主要通过对优良解的统计来构建概率模型以产生优良后代，而几乎完全忽略劣势染色体的相关信息，且目前国内尚未发现将优势基因的链接组合为区块的相关研究。基于此，考虑到PFSP问题属于存在多个局部最优解的组合最优化问题，算法求解时易陷入局部最优，受BBO算法群体迁移的启发，本研究以基本EDA算法为架构，提出一种混合二元分布估计算法(hybrid binary estimation distribution algorithm, HB-EDA)。

1 置换流水车间调度问题数学描述

PFSP问题是典型的生产规划问题，包括n个工件与m台机器，所有的工件遵循同样的加工顺序依次经过所有的机器，目的就是找到一组满足制定目标的最佳排序。最大完工时间(makespan)、总流程时间(total flow time)、总完工时间(total completion time)是调度问题常见的目标。本研究中以最大完工时间作为验证HB-EDA算法的有效性和衡量染色体优劣的标准。

PFSP问题的约束如下：①所有工件的加工顺序相同(依序从机器1到机器m加工)；②每个机器同一时间只能加工一个工件，每个工件同一时刻只能在一台机器上加工；③机器一旦开始加工就不能中断；④所有工件没有优先权。

PFSP问题可以表示为n/m/pij/Cmax，n表示工件数量，m为机器数目，pij表示工件i在机器j上的加工时间，Cmax为总完工时间。考虑工件加工顺序π={π1，π2，…，πn}，令C(πi,j)(i=1,2,…,n)表示工件i在机器j上的完成时间，则PFSP问题的数学模型可表示如下：

C(π1,1)=p(π1,1)

(1)

C(πi,1)=C(πi-1,1)+p(πi,1)

(2)

C(π1,j)=C(π1,j-1)+p(π1,j)

(3)

C(πi,j)=max(C(πi-1,j),C(πi,j-1))+p(πi,j)

(4)

Cmax(π)=C(πn,m)

(5)

i=2,3,…,nj=2,3，…,m

式(1)和式(2)求解第1台机器完工时间；式(3)和式(4)分别表示第1个工件和第i个工件在不同机器上的完工时间；式(5)求解最大完工时间。

2 算法设计

2.1分布估计算法(EDA)

EDA算法最初于1996年被提出，它提出了一种全新的进化模式，并迅速成为进化计算领域的热门研究主题与解决工程问题的有效方法[17]。EDA算法也称为带有概率模块的进化算法(evolutionary algorithms with probability model,EAPM)或者概率模型的遗传算法(probabilistic model-building genetic algorithms,PMBGA)[18]。遗传算法用群体表示优化问题的一组候选解，群体中的个体都有各自的适应度函数，通过个体之间的选择、交叉、变异等操作模拟自然进化机制，并循环执行来对问题求解；而EDA算法是一种基于统计学习的群体进化算法，以学习和挖掘的方式，通过数学模型描述解在搜索空间中的分布情况，利用统计的方式建立概率模型，进而对模型随机采样产生新的种群并反复执行，直到满足终止条件[6，8]。基本EDA算法运作流程如图1所示。

2.2混合二元分布估计算法(HB-EDA)

为更好地利用全局统计信息以增加母体多样性，避免陷入局部最优，以EDA算法为架构，引入BBO算法的迁移操作，以链接区块的形式通过优良解与较差解之间的迁移来更新群体。算法中概率模型分为两种，一种是记录工件位置信息的位置矩阵概率模型，用于组合链接区块；另一种是记录工件先后关系的相依矩阵概率模型，将其与位置概率结合为合并概率，用于后期染色体重组。算法步骤如下：

(1)母体初始化。为保证初始解的质量和随机性，HB-EDA算法以随机方式和NEH启发式方法产生初始解。

(2)计算适应度。将初始解按适应度大小排序，取前30%为优势群，后70%为劣势群，依平均适应度计算迁移比率。

(3)更新概率矩阵模型。根据优势群建立位置概率模型1和相依概率模型，根据劣势群建立位置概率模型2，然后分别按照两位置概率模型组合区块。

(4)产生子代。模拟BBO算法的迁移操作，使用两类链接区块组合新的染色体产生子代。

(5)染色体重组。将染色体执行切段并重组，以进一步寻优。

(6)取代。筛选母体与子代中具有高度竞争优势的解组成新的母体进入下一代进化操作。重复执行步骤(3)～步骤(6)，直到满足终止条件。

HB-EDA算法流程图见图2。其中，ΔR为更新概率模型的计数器，Rthre为更新概率模型的阈值，ΔA和Athre分别为组合人造解的计数器和阈值。

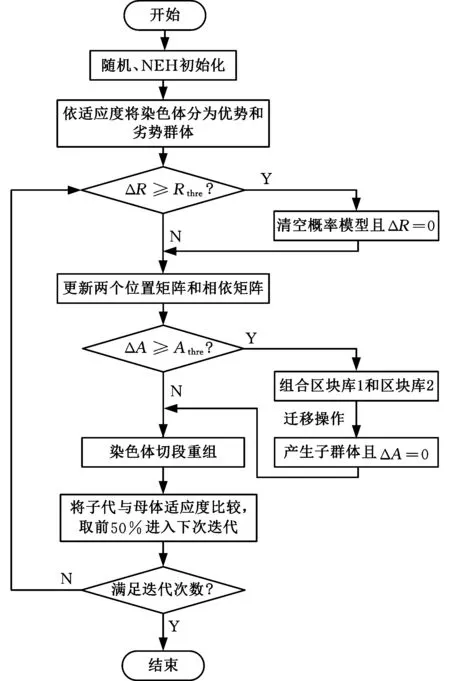
图2 HB-EDA算法流程图Fig.2 Flow chart of HB-EDA

2.2.1初始解的产生

为兼顾初始解的多样性与质量，HB-EDA算法采用完全随机生成与NEH启发式构造两种方法产生初始解，其中NEH产生解时仅针对1/2的工件构造，剩余工件随机插入解序列中。NEH启发式算法的核心思想就是赋予总加工时间最大的工件以优先权[19]，其步骤如下：

(1)对所有n个工件的每个工件i，计算其在所有m台机器上的总加工时间：

(6)

i=1,2,…,nj=1,2,…,m

式中，ti,j为工件i在机器j上的加工时间。

(2)把所有计算出的Ti按下降顺序排列，取总加工时间最大的两个工件，分别计算这两个工件局部完工时间，按完工时间较小的序列排列两个工件。

(3)从i=3,4，…,n，把k个工件插入k个可能的位置，求得最小的部分完工时间。

2.2.2构建概率矩阵模型

HB-EDA算法使用位置矩阵和相依矩阵来更新概率模型。位置矩阵记录的是工件的位置信息，而相依矩阵描述的是工件间的位置关系。两矩阵都以世代累加的方式不断增加。通过建立位置矩阵从前N%(Nlt;100)的优势解中挖掘出优势区块组成区块库1，从后1-N%的劣势解中挖掘出劣势区块组成区块库2。由于优势解常具有类似的基因结构，本研究借由区块库2中的劣势区块更新部分优势解，以增加多样性，跳出局部最优。位置矩阵按以下方式更新：

(7)

i=1,2,…,nj=1,2,…,nk=1,2,…,K

(8)

i=1,2,…,nj=1,2,…,n

t=1,2,…,Gk=1,2,…,K

图3为位置矩阵的更新方式，假设P1,P2,…，P5是用于更新位置矩阵的染色体，根据染色体序列上工件位置统计信息，以P31为例，工件3在位置1出现了3次，因此P31概率为3/5。

图3 位置矩阵示意图Fig.3 Schematic diagram of position matrix

(9)

图4 相依矩阵示意图Fig.4 Schematic diagram of dependency matrix

Dij为工件i直接出现在工件j后面的次数：

(10)

t=1,2,…,G

假设P1,P2，…，P5共5条染色体是用于更新位置矩阵的染色体，根据染色体序列上工件前后关系统计信息，以D14为例，工件1紧连工件4后面出现了2次，因此D14概率为2/5。

2.2.3构建链接区块

区块是通过对染色体的统计与采样而提取出的高频基因链接组合[20]。通过组合区块降低问题的维度是非常有效的一种方式，不仅能够快速找到良好解的排序，而且能够加速收敛时间。如图5所示，以单机10工件的调度问题为例，其解空间为10！。通过挖掘优势区块组合{B(1)，B(2)，B(3)，B(4)}，可行解空间变为6！，极大地降低了可行解维度。

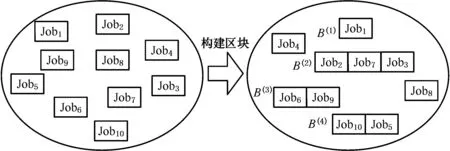
图5 复杂度降低Fig.5 Complexity reduction

由于流水车间工件排序问题最主要是确定工件的加工顺序，因此工件的位置相对重要。为降低运算复杂度，本研究中区块挖掘仅根据位置矩阵提供的信息进行挖掘。首先以随机的方式选择区块的起始位置，产生符合最小区块长度的空白区块段，之后将挑选最合适的区块放入区块段。将位置矩阵中的信息转化为概率，以轮盘赌的方式进行工件选择。每增加一个工件便计算区块总体概率，概率越小说明错误率越高，文中设立总体概率的门槛值，仅挖掘满足门槛值区块长度的区块。例如，由4个工件{1,2,3,4}组成的区块，各个工件的概率分别为0.4,0.3,0.5,0.7，此区块的总体概率为0.4×0.3×0.5×0.7=0.052，代表此区块的总体正确率为0.052。由此可见，区块长度越长，错误率越高。本文设立的区块门槛值随着进化代数的增加从0.5增大到0.8。区块组合步骤如图6所示。

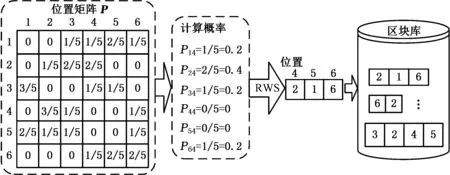
图6 区块挖掘方式Fig.6 Block mining method

区块组合完成后，将每一世代中新产生的区块与区块库中的区块进行筛选与比较，最终挑选出竞争优势较大的区块。区块竞争主要有两步：

(1) 首先对区块库中的区块进行位置比对，如果位置出现重复则通过对区块的平均概率比较将概率较小的区块删除。

(2)对工件进行比较，若区块中包含的工件出现重复，则对区块平均概率进行比较，删除概率较小的区块。经过区块竞争后保留下来的区块没有重复的位置和工件。区块n的平均概率

(11)

其中，B(n)表示第n个区块；l为区块长度；P(p)为根据位置矩阵计算的概率。

2.2.4产生子代

BBO算法中，算法由多个栖息地组成，每个栖息地具有不同的适宜度指数(habitat suitable index，HSI)。与栖息地适宜度指数相关的特征包括温湿度、栖息地的降雨量、植被多样性、气候等因素，这些特征构成描述栖息地适宜度的向量。具有较高HSI的栖息地趋向于承载较大的种群，而较低HSI的栖息地能容纳的种群数量较少[15-16]。BBO算法主要通过种群迁移和变异来更新解。迁移率计算公式如下：

(12)

(13)

I，E∈(0，1]

其中，Smax为栖息地最大可能容纳种群数；λ为迁入率；μ为迁出率；r为当前栖息地物种数量；I为最大迁入指数；E为最大迁出指数。

HB-EDA算法通过两个区块库与母体优势染色体和劣势染色体之间的迁移操作来更新母体。分别计算前N%的解和后1-N%的解的平均适应度f1和f2，设定迁出率μ=f2/(f1+f2)，迁入率λ=1-μ。本研究提出的HB-EDA算法首先将母体分为前N%的优势解群体与后1-N%的劣势解群体，根据优势解群体建立区块库1，根据劣势解群体建立区块库2。考虑到适应度高的解序列都具有相似的片段结构，演化过程中优势解群体易陷入局部最优，难以出现新的性状，因此考虑使利用区块库2中的区块来更新部分优势染色体，以增加染色体的多样性，从而能够搜索到按照常规变动方式难以到达的区域，扩大搜索空间。如图7所示，对于前N%的染色体(前10条作为精英解保留)，首先从区块库2中以迁入率λ选出区块，将各个区块的起始工件与母体进行比较，若工件相同，将区块替换到母体中，更新后，将染色体中重复出现的工件删除，按原染色体的序列将未放置的工件填入。对于后1-N%的染色体，由于已经由借助其解序列挖掘出带有新颖信息的区块保存到区块库2中，故对于后1-N%条染色体采取完全更新操作。首先从区块库1中以迁出率μ选出区块按照起始位置大小的顺序复制到染色体中，如图7所示，未排列工件的位置为位置3、位置7、位置10，按照位置大小顺序从位置3开始选择工件；依照合并概率以RWS方法选择工件10放入，同理，将工件2和工件9分别放入位置7和位置10；借助两个区块库更新母体的操作就是将适宜度低的群体以较大的概率接受移入，即适宜度高的群体的特征变量以较大概率被传播。通过执行迁移操作，所有的母体得到更新。合并概率

(14)

i,j,k=1,2,…,ni≠j

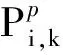
图7 执行迁移操作组合人造解Fig.7 Perform migration operation to combine artificial solution

2.2.5染色体重组

为提高HB-EDA算法找寻最佳解的机会，对染色体进行重组。首先随机选择NC个切点，将染色体随机分割成NC+1个片段，对切出的最长的片段进行重组。如图8所示，位置4到位置8为切出的最大片段，针对这个片段，首先计算位于片段紧前工件后未出现的所有工件的合并概率，以RWS方法选择工件放入片段中，之后以相同的方法继续选择下个工件，直到完成片段重组。

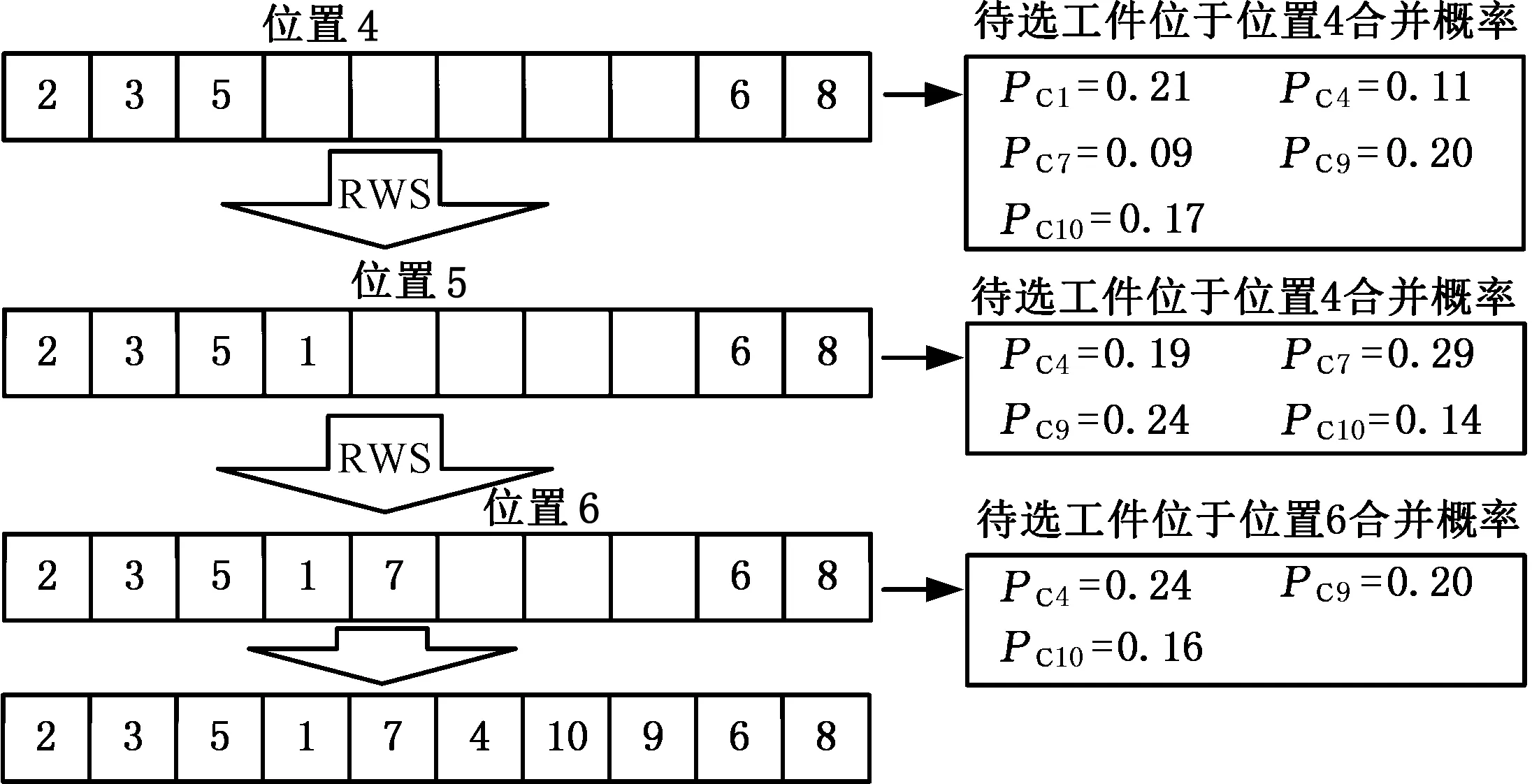
图8 染色体重组原理图Fig.8 Schematic diagram of chromosome recombination

3 实例仿真与结果分析

为验证提出的HB-EDA算法的求解能力，进行了实例仿真。测试数据采用REEVES[21]和TAILLARD[22]提出的基准测试问题，应用所提算法求解这些基准实例，并与其他文献算法进行比较，以验证所提出算法的有效性。HB-EDA算法程序由VS 2010中的VC++编写，在Windows 7

32位系统、主频2.4G的酷睿CPU、2G内存的普通电脑上执行实验测试。本研究以平均误差率(ARE)和最小值误差率(BRE)为比较标准，每个例题独立运行30次。计算公式如下：

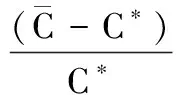
(15)

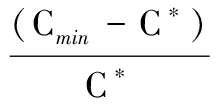
(16)

选择21种Reeves例题进行测试并与文献[16]提出的混合离散的生物地理学算法(HDBBO)、文献[23]提出的基于单变量EDA组合区块的进化算法(BBEA)、文献[24]提出的将使用概率模型产生的人造解与遗传算法结合的混合算法(ACGA)的结果进行比较。参数设置如下：种群规模为100，迭代次数为50倍的机器数与工件数的乘积。表1给出了算法对Reeves例题测试结果和最优值的比较。由表1可知，HB-EDA算法的求解能力整体上优于HDBBO算法、BBEA算法、ACGA算法。

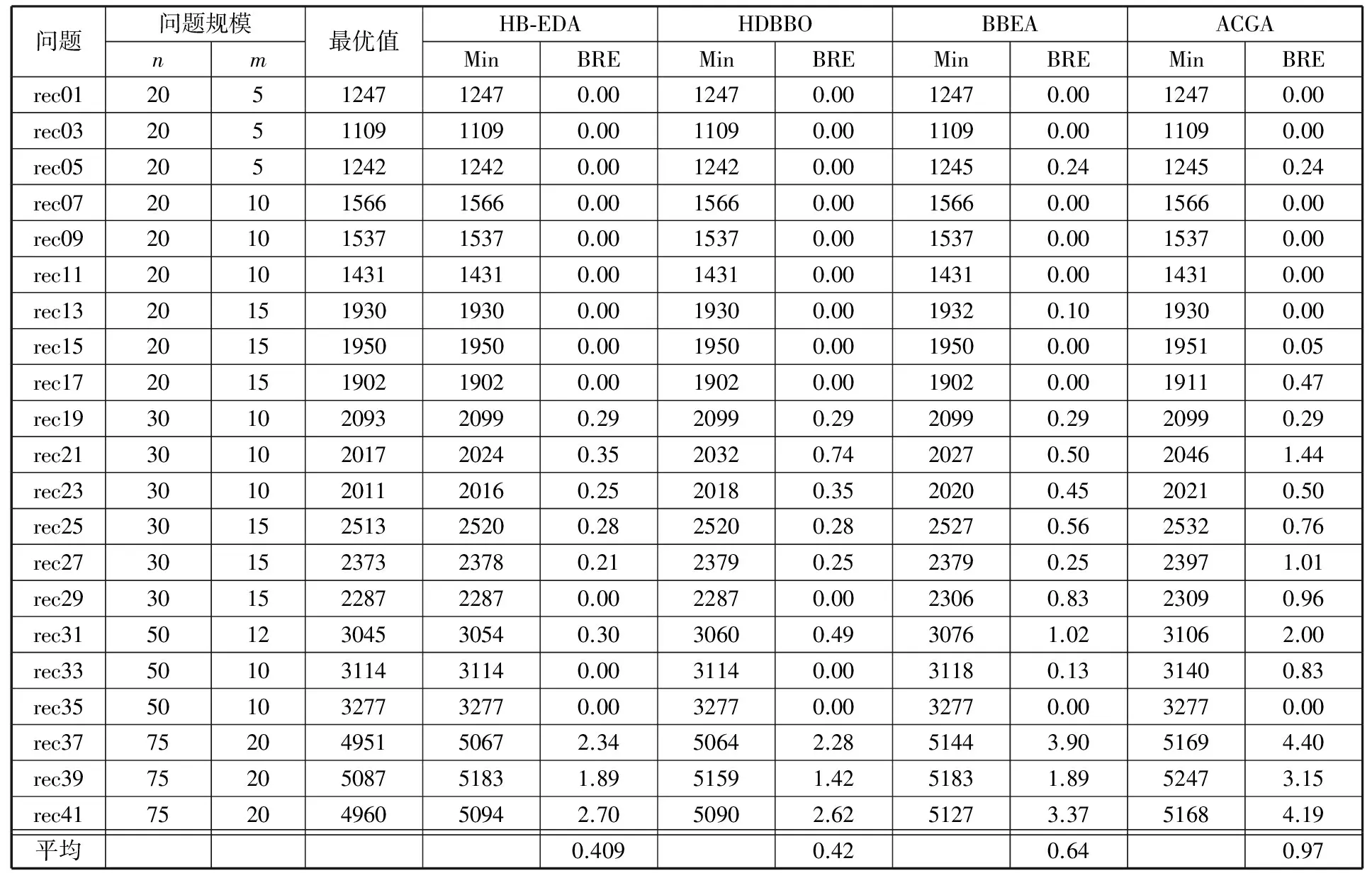
表1 Reeves案例测试结果比较

表2给出了HB-EDA算法对Taillard例题测试的最小值误差与平均值误差，并与基本EDA算法、文献[25]提出的PSO-Lian算法、BBEA算法[23]、文献[20]提出的基于区块的分布估计算法(BBEDA)比较，执行代数与文献[25]相同。结果显示，除Ta050和Ta060外，其他测试例题均找到了目前已知的下限值。

表2 Taillard案例测试结果比较

为更直观地比较算法性能，图9和图10给出了HB-EDA算法和BBEDA算法在求解ta030和ta060的收敛图。由图可知，在执行世代数相同的情况下，HB-EDA算法的收敛速度和求解质量优于BBEDA算法。HB-EDA算法的求解机制在初始化时运用了NEH启发式构造，既保证了初始解的质量，同时兼顾了初始解的随机性。算法以区块的形式进行全局更新，极大地增加了搜寻的多样性与求解效率，易跳出局部最优。

图9 Ta030收敛图Fig.9 Ta030 convergence graph

图10 Ta060收敛图Fig.10 Ta060 convergence graph

4 结束语

本研究针对置换流水车间调度问题提出了一种混合二元分布估计算法的优化算法(HB-EDA)。算法采用NEH与随机产生的方法生成初始解，兼顾了初始解的质量和多样性；借助优势和劣势区块库执行迁移操作更新群体，保证了搜索空间的多样性与效率。传统EDA算法忽略了劣势解蕴含的信息，而HB-EDA算法则搜集全局信息，算法中使用劣势区块更新部分优势解的操作在一定程度上类似遗传算法中的突变操作，但效率更高。数值测试结果表明，该算法具有较强的搜寻能力与求解效果。

算法仅针对单目标置换流水车间调度问题进行求解，为提高HB-EDA算法的适用性，下一步将尝试解决其他类型的组合型问题，如TSP问题、作业车间调度、无等待流水车间调度以及考虑多目标调度等问题。此外，算法组合区块仅仅考虑基因为连续的情况，组合不连续的优秀片段和劣势片段以更新群体将是未来研究的方向。

[1] GAREY M R, JOHNSON D S. Computers and Intractability: a Guide to the Theory of NP-Completeness [M]. San Francisco：W.H. Freeman and Company, 1979:11-19.

[2] CHUNG C S, FLYNN J, KIRCA O. A Branch and Bound Algorithm to Minimize the Total Flow Time for M-machine Permutation Flowshop Problems[J]. International Journal of Production Economics, 2002, 79(3)：185-196.

[3] FRAMINAN J M, GUPTA J N D, LEISTEN R. A Review and Classification of Heuristics for Permutation Flow-shop Scheduling with Makespan Objective[J]. Journal of the Operational Research Society, 2004, 55(12): 1243-1255.

[4] RUIZ R, MAROTO C. A Comprehensive Review and Evaluation of Permutation Flowshop Heuristics[J]. European Journal of Operational Research, 2005, 165(2): 479-494.

[5] CEBERIO J, IRUROZKI E, MENDIBURU A, et al. A Review on Estimation of Distribution Algorihms in Permutation-based Combinatorial Optimization Problems [J]. Progress in Artificial Intelligence，2012，1(1)：103-117.

[6] 王圣尧，王凌，方晨，等. 分布估计算法研究进展[J]. 控制与决策，2012，27(7)：961-966.

WANG Shengyao, WANG Ling, FANG Chen, et al. Advances in Estimation of Distribution Algorithms[J]. Control and Decision, 2012, 27(7)：961-966.

[7] LIMA C F, PELIKAN M, LOBO F G, et al. Loopy Substructural Local Search for the Bayesian Optimization Algorithm[C]// International Workshop on Engineering Stochastic Local Search Algorithms. Berlin：Springer，2009：61-75.

[8] LARRAANAGA P, LOZANO J A. Estimation of Distribution Algorithms: a New Tool for Evolutionary Computation [M]. New York：Springer US，2002:1140-1148.

[9] LIU H, GAO L, PAN Q. A Hybrid Particle Swarm Optimization with Estimation of Distribution Algorithm for Solving Permutation Flowshop Scheduling Problem[J]. Expert Systems with Applications，2011，38(4)：4348-4360.

[10] TZENG Y R, CHEN C L, CHEN C L. A Hybrid EDA with ACS for Solving Permutation Flow Shop Scheduling[J]. The International Journal of Advanced Manufacturing Technology，2012，60(9/12)：1139-1147.

[11] ROBLES V, PEA J M, LARRAAGA P, et al. GA-EDA: a New Hybrid Cooperative Search Evolutionary Algorithm[M]// Towards a New Evolutionary Computation. Berlin: Springer, 2006:187-219.

[12] 叶宝林，高慧敏，王筱萍，等. 基于分布估计算法的二阶段置换流水车间调度算法[J]. 计算机应用研究，2011，28(10)：3702-3706.

YE Baolin，GAO Huimin，WANG Xiaoping，et al. Two-stage Algorithm Based on Estimation of Distribution Algorithm for Permutation Flow-shop Scheduling Problem[J]. Application Research of Computers, 2011，28(10)：3702-3706.

[13] 孙良旭，曲殿利，刘国莉. 置换流水车间调度问题的两阶段分布估计算法[J]. 计算机工程与应用，2017，53(2)：64-71.

SUN Liangxu，QU Dianli，LIU Guoli. Two-stage Estimation Distribution Algorithm for Permutation Flowshop Scheduling Problem[J]. Computer Engineering and Applications，2017, 53(2)：64-71.

[14] 何小娟，曾建潮.基于Bayesian统计推理的分布估计算法求解柔性作业车间调度问题[J]. 系统工程理论与实践，2012, 32(2)：380-388.

HE Xiaojuan，ZENG Jianchao. Solving Flexible Job-shop Scheduling Problems with Bayesian Statistical Inference-based Estimation of Distribution Algorithm[J]. Systems Engineering-Theory amp; Practice，2012，32(2)：380-388.

[15] SIMON D. Biogeography-based Optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(6)：702-713.

[16] LIN J. A Hybrid Discrete Biogeography-based Optimization for the Permutation Flow Shop Scheduling Problem[J]. International Journal of Production Research，2015: 4805-4814.

[17] MÜHLENBEIN H, PAASS G. From Recombination of Genes to the Estimation of Distributions I. Binary Parameters[M]// Parallel Problem Solving from Nature—PPSN IV. Berlin： Springer，1996:178-187.

[18] CHANG P C，HUANG W H，WU J L，et al. A Block Mining and Re-combination Enhanced Genetic Algorithm for the Permutation Flowshop Scheduling Problem[J]. International Journal of Production Economics, 2013, 141(1)：45-55.

[19] NAWAZ M，ENSCORE E E，HAM I. A Heuristic Algorithm for the M-machine，N-job Flow-shop Sequencing Problem[J]. Omega, 1983, 11(1): 91-95.

[20] CHANG P C, CHEN M H. A Block Based Estimation of Distribution Algorithm Using Bivariate Model for Scheduling Problems[J]. Soft Computing，2014，18(6): 1177-1188.

[21] REEVES C R. A Genetic Algorithm for Flowshop Sequencing[J]. Computers and Operations Research，1995，22(1)：5-13.

[22] TAILLARD E. Benchmarks for Basic Scheduling Problems[J]. European Journal of Operational Research，1993，64 (2)：278-285.

[23] CHANG P C，CHEN M H，TIWARI M K，et al. A Block-based Evolutionary Algorithm for Flow-shop Scheduling Problem[J]. Applied Soft Computing，2013，13(12)：4536-4547.

[24] CHANG P C，CHEN S H，FAN C Y，et al. Generating Artificial Chromosomes with Probability Control in Genetic Algorithm for Machine Scheduling Problems[J]. Annals of Operations Research，2010，180(1)：197-211.

[25] LIAN Z，GU X，JIAO B. A Similar Particle Swarm Optimization Algorithm for Permutation Flowshop Scheduling to Minimize Makespan[J]. Applied Mathematics and Computation，2006，175(1)：773-785.

(编辑王旻玥)

PermutationFlowShopSchedulingProblemBasedonHybridBinaryDistributionEstimationAlgorithm

PEI Xiaobing ZHAO Heng

School of Management,Tianjin University of Technology,Tianjin,300384

To solve the permutation flow shop scheduling problems with the objective of minimizing makespan, an effective new hybrid binary estimation distribution algorithm(HB-EDA) was proposed based on binary estimation of distribution algorithm and BBO. HB-EDA took distribution estimation algorithm as architecture and the binary probability model was used as the evolutionary basis. For the excellent chromosomes and the inferior chromosomes, the link gene blocks with the dominant informations and the disadvantage informations were excavated by the probability model, these blocks were reserved in two archives for future use. Integrating with migration operator of BBO, two block archives were used to update maternal chromosomes with certain migration rate to generate sub-groups, then performing segmentation and recombination on the chromosomes to further selecting high fitness solution. Simulation results on Reeves and Taillard suites and comparisons with other algorithms validate the excellent searching ability and efficiency of the proposed algorithm.

permutation flow shop scheduling; biogeography-based optimization(BBO); distribution estimation algorithm; building block

TP18

10.3969/j.issn.1004-132X.2017.22.016

2016-12-01

天津市哲学社会科学规划项目(TJYY17-013)

裴小兵，男，1965年生。天津理工大学管理学院教授。主要研究方向为生产调度、精益生产与管理。赵衡(通信作者)，男，1992年生。天津理工大学管理学院硕士研究生。E-mail:gongye_tjut@126.com。