基于快速正交搜索的车载导航方法

王志伟，秦俊奇，杨功流，石志勇，狄长春，王风杰

（1.军械工程学院，石家庄 050003；2.北京航空航天大学，北京 100191；3.陕西华阴63870部队，华阴 714200）

基于快速正交搜索的车载导航方法

王志伟1，秦俊奇1，杨功流2，石志勇1，狄长春1，王风杰3

（1.军械工程学院，石家庄 050003；2.北京航空航天大学，北京 100191；3.陕西华阴63870部队，华阴 714200）

以某型自行火炮炮载惯导系统为研究对象，针对系统剩余高阶非线性误差得不到有效补偿的问题，结合卡尔曼滤波（KF），提出了基于快速正交搜索（FOS）的组合估计方法，既消除了线性误差，也对系统的高阶非线性误差起到了良好的抑制作用。试验结果表明，在没有卫星信号的情况下，与单独使用KF相比，FOS/KF可以有效提高导航精度，经过补偿后的平均水平速度误差仅为0.034 m/s，定位误差可基本保持在10 m以内，实现了非线性条件下的高精度自主导航。

自行火炮；非线性误差；快速正交搜索算法；捷联惯性导航系统

在有卫星信号辅助的情况下，炮载导航可以达到很高的精度。但是在遮蔽的情况下卫星信号不稳定，并且在战场环境下有多种手段和方法可以屏蔽卫星信号，甚至使卫星失灵，从而导致武器装备不能进行有效导航[1-3]。针对以上问题，自主导航成为现阶段研究的热点之一，卡尔曼滤波（KF）作为一种有效的参数估计手段，广泛应用到多种自主导航的过程中[4-5]。众所周知，KF只能在线性环境下工作，一旦系统发生非线性，KF就会产生非线性估计误差，导致导航误差增大。而在实际导航过程中，很难保证系统模型线性[6-8]。为了避免建立模型带来的估计误差，各种神经网络算法相继被提出，但是神经网络有一个致命的弱点，就是容易陷入局部极小点，并且需要依靠耗时的迭代算法来实现，不仅训练时间长，而且算法精度有待提高[9-10]。本文利用快速正交搜索算法（Fast orthogonal search,FOS）有效避免了上述问题的发生。FOS算法是由美国学者Korenberg在1989年提出的[11]，该算法类似于有导师的神经网络算法，需要已知的训练数据，并通过最大限度地减小估计量和训练量之间的均方误差实现参数估计。但是相比神经网络，FOS不需要频繁的迭代过程，而是通过一次迭代就能确定出合适的系统模型项。相比传统的最小二乘方法，通过FOS所建立的系统模型中包含更少的模型项，这就大大减小了噪声的干扰，提高了估计精度[12-15]。目前，FOS算法在许多领域中已有应用，包括信号压缩、磁共振成像、正电子发射断层扫描、非线性系统控制以及基因识别技术等，但是FOS算法在导航领域的应用几乎没有。

本文将FOS算法与KF相结合，分析了炮载惯导应用环境，在有卫星信号时，利用卫星数据作为FOS的训练数据，进行系统模型训练，在没有卫星信号时利用训练所得的系统模型进行参数估计，实现了非线性条件下的高精度导航。

1 系统非线性误差

式中：M为子午圈半径；N为卯酉圈半径；为加速度计输出；为陀螺输出；o(·)为相关误差参数的高阶项。由于KF只适用于线性系统，所以非线性系统在经过KF估计补偿后仍然含有剩余高阶非线性误差项，即o(·)导致了剩余高阶非线性误差项的产生。

为了避免KF在使用过程中的局限性，提高导航精度，有必要对相关误差参数的高阶项o(·)进行补偿。建立非线性模型如下：

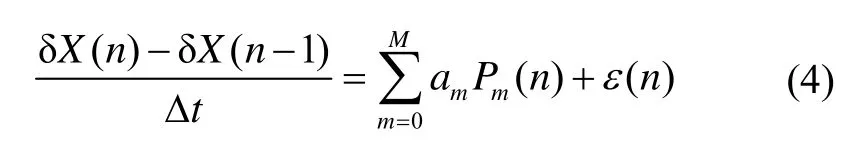
所提方法具有以下特点：

1） 该方法可以估计主要的非线性误差参数以及与其对应的权值系数；

2） 当GPS可用时，以GPS信息为训练值，可以建立与当前系统高度匹配的非线性误差模型；

3） 当GPS不可用时，可以利用2）中建立的误差模型进行误差估计；

4） 该方法具有很高的实时性。

2 快速正交搜索

2.1 系统模型

非线性系统可表示为如下形式：

式中：F为非线性函数；x(n-L)为系统输入，y(n-K)为系统输出，ε(n)为系统误差，为计算过程的时间延迟，采样次数

非线性系统(1)可被表示为

式中：i、j分别为系统输入和输出的维数。系统的均方误差（MSE）可表示为：

式(9)中的直线表示取从n=N0到n=N的平均值。该算法的核心原则就是根据均方误差的大小来确定系统模型项

2.2 详细搜索过程

将式(1)中的系统进行Gram-schmidt（GS）正交化得到：

此时，均方误差和正交权值系数变为：

完成搜索的条件有三个：

1） 当剩余均方误差MSEm足够小时完成搜索；

2） 当误差模型项达到设定上限时完成搜索；

3） 当剩余候选函数不能使均方误差产生足够大的减小量时完成搜索。

当搜索完成后，利用αmr和gm计算出与所选模型项对应的权值系数am，过程如下：

综上，FOS的基本原理可以定义为：利用GS正交化方法建立正交系数αmr，然后利用αmr计算权值系数gm，并根据对均方误差影响最大的原则选出候选函数最后将对应的gm与系统输出y(n)进行关联，计算出正交化之前的权值系数am。

类比式(11)定义函数D(m,r)和C(m)，表示三者之间的关系如下：

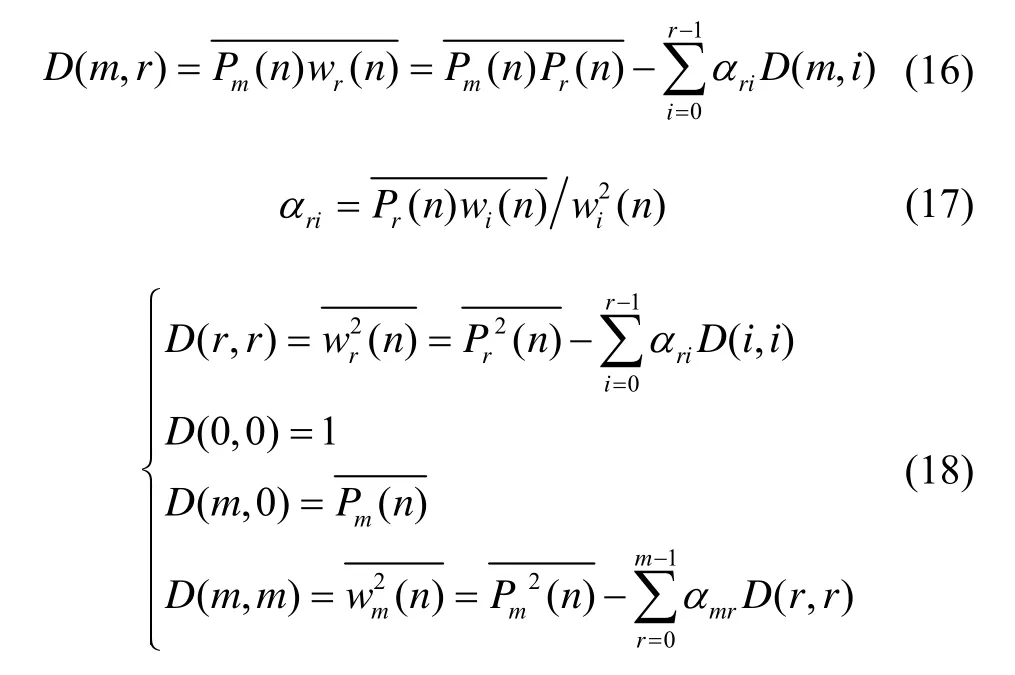
将式αmr、gm和MSE的减小量Qm重新表示如下：

FOS简要计算过程如下：

3） 重复步骤1）和2）直到满足搜索完成的条件为止；

4） 计算正交化之前的权值系数am，构建系统模型。

相比数学方法，FOS更加直接地作用于误差参数本身。在有卫星信号的时候，多种信息可以在线训练FOS。同时，以均方误差为标准，选取合适的候选函数，使得FOS能够准确地感知出误差项及其权重。这样，尽管训练时间很短，FOS依旧可以在没有先验信息的情况下较好地反映出当前误差模型的主要特征。与其他方法不同的是，FOS无需模拟动态非线性系统，而是根据模型项的权重以数学模型的形式将其表示出来，并利用所构建的数学模型在线更新非线性系统模型。如此，通过FOS构建的系统模型可以保证在动态条件下的估计精度。另外，只要能保证训练数据的准确性，无论失去卫星信号的时间长与短，FOS都可以提供高精度的估计结果。

3 FOS/KF组合估计方法

在导航解算过程中加入FOS算法，首先利用KF对系统的线性误差进行估计，然后利用FOS估计出剩余系统非线性误差，形成了 FOS/KF算法。式(1)～(3)中均包含o(δP)和o(δV)，表明非线性位置和速度误差会影响导航结果，而位置误差又源于速度误差，所以这里利用FOS对速度误差的非线性相关项进行估计。各个误差项的关系如下：

式中：ΔV为剩余非线性速度误差；VINS为导航解算得到的速度；VGPS为卫星测量得到的速度；δVKF为KF滤波得到的速度误差。

整个过程分为两个阶段：第一个阶段式模型训练阶段，在GPS可用时进行，目的是通过外部高精度信息对系统进行训练，得到由多个候选函数组成的系统模型；第二个阶段是估计阶段，GPS不可用时进行，利用在模型训练阶段训练好的系统模型进行参数估计。

3.1 模型训练阶段

当GPS信息可用时，将式(25)得出剩余非线性速度误差ΔV作为输出，将 KF预测值作为输入，组成一组训练值，进行模型训练。训练流程如图1所示，其中，为导航解算得到的位置、速度、姿态信息，为GPS量测信息，为卡尔曼滤波的估计值。

为对应第3节中的各个变量，令输入维数i=9，输出维数j=3，采样次数N=500，M=30，N0=5，候选函数总的个数约为80000。

图1 模型训练示意图Fig.1 Model training sketch

3.2 预测阶段

每当失去GPS信号时，系统不能直接求得精确的剩余非线性速度误差ΔV，此时FOS按照4.1中的过程进行在线建模，结合 KF预测值对ΔV进行估计，补偿速度输出，并利用补偿后的速度信息计算当前的位置信息，具体流程如图2所示。

图2 误差预测示意图Fig.2 Error prediction

4 实车试验

为验证FOS/KF方法的可行性，进行了实车试验，试验于2017年1月在北京进行，行车路线选取北京西北六环，载车为某型轮式自行火炮，试验对象为该型自行火炮所搭载的惯性导航系统，惯组更新频率为100 Hz，陀螺常值漂移为 0.05 (°)/h，量测范围为 300(°)/s，随机游走系数为加速度计零偏为150 μg，量测范围为±10g，随机噪声为GPS水平定位精度为5 m，高程定位精度为10 m，测速噪声为0.1 m/s。

4.1 跑车条件

为了对所提方法进行充分验证，整个试验被分为11个阶段，进行11次重复验证。每个阶段时长为800 s，前500 s所采集的数据为训练数据，后300 s采集的数据为验证数据，整个试验过程时长12 329 s。在每个阶段开始前需要停车关机不少于2 min，确保每个阶段具有相同的初始物理状态。

图3为跑车的详细数据，包括跑车路径、车速以及跑车里程等信息。图4为炮载惯性导航系统（采样频率为100 Hz）。图5为自行火炮外部搭载的GPS天线（采样频率为1 Hz）和电台天线。图6为位于火炮内部的数据处理设备。从图中速度数据可明显看出，车辆每隔一段时间就会停止一次，停止过后进行下一次数据采集，一共11次。

图3 跑车路径及详细信息Fig.3 Test path and detailed information

图4 炮载惯导Fig.4 Gun-board SINS

图5 GPS天线Fig.5 GPS antenna

图6 数据处理设备Fig.6 Data processing equipment

4.2 试验结论

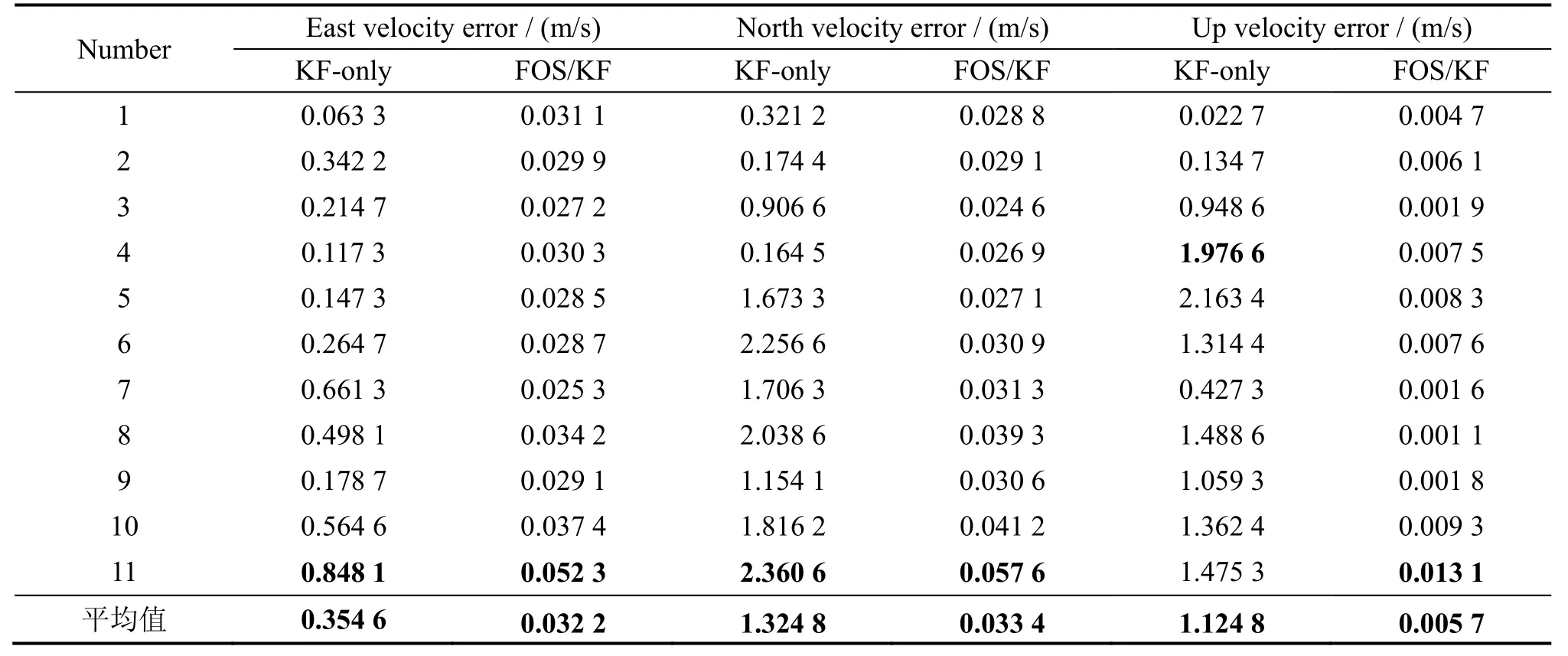
表1 速度误差对比Tab.1 Contra st on velocity errors

表1为每个阶段三个方向的平均速度误差。对比两种方法的估计结果，当使用KF单独估计时，三个方向的平均速度误差分别为0.354 5 5 m/s、1.323 7 m/s、1.124 5 m/s。造成该误差的主要原因是惯导自身的零偏和常值漂移，尤其是陀螺的常值漂移。尽管部分误差已被KF估计出来，但是剩余的高阶非线性误差仍造成误差随着时间的推移快速增长。当使用FK/FOS 组合估计方法进行估计时，三个方向上的平均误差减少到0.032 2 m/s、0.033 4 m/s、0.005 7 m/s。这说明FOS可以很好地对剩余高阶非线性误差进行估计和补偿。

另外，对比每个方向11个阶段的估计结果，在使用FK/FOS方法进行估计时，最大值仅为0.052 3 m/s、0.057 6 m/s、0.013 1 m/s。由于系统随时间不断变化，说明FOS估计方法可以很好地适应动态环境。

图7～9分别为三个方向上速度误差的对比曲线，可以看出，FK/FOS对实际系统的误差抑制效果十分显著。

图7 平均东向速度误差Fig.7 Average east velocity error

图8 平均北向速度误差Fig.8 Average north-velocity error

图9 平均天向速度误差Fig.9 Average up velocity error

表2中对比了两种方法所得到的位置误差，三个方向上的平均值分别为19.000 3 m、21.215 8 m、8.056 9 m和5.856 1 m、8.004 5 m、2.090 0 m。结果进一步说明了KF不能对剩余非线误差进行有效估计，也说明了经过FOS估计和补偿后，位置误差得到了显著改善。

图 10～12分别为三个方向上位置误差的对比曲线，由于位置信息是通过速度信息直接求取的，所以利用补偿后的速度计算出的位置误差有明显减少。

图10 平均东向位置误差Fig.10 Average east position error

图11 平均北向位置误差Fig.11 Average north position error

图12 平均天向位置误差Fig.12 Average up position error

图 13为载体运行过程中方向角的变化曲线。图14为经过两种方法估计补偿后的方向角误差对比图，其中的各点处的数值对应 11个验证过程中选取的各个过程中最大的方位角误差值。显然，方向角误差的大小与剩余非线性误差有着很大关系，这与式(2)一致。

图13 方位角Fig.13 Azimuth

表2 位置误差对比Tab.2 Contrast on position errors

图14 每300 s中的最大方位误差角Fig.14 Maximum azimuth in every 300 s

5 结 论

在分析惯导误差的基础上，提出将FOS算法加入到导航过程中，利用FOS对系统的剩余非线性误差进行估计，与KF配合工作，形成了KF/FOS组合估计算法。对比分析两种方法在实际跑车过程中的结果，说明KF/FOS算法可以有效估计系统剩余非线性高阶误差，并且通过对速度误差的补偿可以有效降低定位和测姿误差，为动态条件下的高精度导航提供了方法和手段。

（References）：

[1]房建成, 申功勋.车载DR系统自适应扩展卡尔曼滤波模型的建立及仿真研究[J].中国惯性技术学报, 1998,6(3): 24-28.Fang J C, Shen G X.Modeling and simulation of the self-adaptive filtering in landing vehicle DR system[J].Journal of Chinese Inertial Technology, 1998, 6(3): 24-28.

[2]吴文启, 何晓峰, 胡小平.导航技术发展研究[R].控制科学与工程科学发展报告, 2014: 1378-1381.Wu W Q, He X F, Hu X P.Highlights in navigation research[R].Development of Control Science and Engineering Science, 2014: 1378-1381.

[3]周永余, 陈永冰, 李文魁.21世纪初舰船组合导航系统的发展趋势[J].海军工程大学学报, 2002, 14(6): 46-51.Zhou Y Y, Chen Y B, Li W K.Development trend of the combined ship navigation system in the early part of the 21st century[J].Journal of Naval University of Engineering, 2002, 14(6): 46-51.

[4]Dissanayake G, Sukkarieh S, Nebot E, et al.The aiding of a low-cost strapdown inertial measurement unit using vehicle model constraints for land vehicle applications[J].IEEE Transactions on Robotics and Automation, 2001,17(5): 731-747.

[5]Niu X, El-Sheimy N.Development of a low-cost MEMS IMU/GPS navigation system for land vehicles using auxiliary velocity updates in the body frame[C]//Proceedings of ION GNSS.CA, 2005: 2003-2012.

[6]Gustafsson F.Particle filter theory and practice with positioning applications[J].IEEE Aerospace and Electronic Systems Magazine, 2015, 25(7): 53-82.

[7]Regulski P, Terzija V.Estimation of frequency and fundamental power components using an unscented Kalman filter[J].IEEE Transactions on Instrumentation and Measurement, 2015, 61(4): 952-962.

[8]Pasha S A, Hoang D T, Vo B N.Nonlinear baysian filtering using the unscented linear fractional transformation model[J].IEEE Transactions on Signal Processing, 2013, 58(2): 477-489.

[9]Wang X Y, Huang Y.Convergence study in extended Kalman filter-based training of recurrent neural networks[J].IEEE Trans on Neural Networks, 2015, 22(4): 588-600.[10]Gan X S, Jing D M, Wei C.Wavelet neural network based on SSUKF and its applications in aerodynamic force modeling for flight vehicle[C]//International Conference on Measuring Technology and Mechatronics Automation.2013: 1087-1090.

[11]Korenberg M J.A robust orthogonal algorithm for system identification and time series analysis[J].Biological Cybernetics, 1989, 60(4): 267-276

[12]Korenberg M J.Identification nonlinear difference equation and functional expansion representations: the fast orthogonal algorithm[J].Annals of Biomedical Engineering,1988, 16, 123-142.

[13]Korenberg M J, Paarmann L D.Applications of fast orthogonal search: time-series analysis and resolution of signals in noise[J].Annals of Biomedical Engineering,1989, 17(3): 219-231.

[14]Eklund J M, Korenberg M J, McLellan P J.Nonlinear system identification and control of chemical processes using fast orthogonal search[J].Journal of Process Control,2007, 17(9): 742-754.

[15]Korenberg M J, Paarmann L D.Orthogonal approaches to time-series analysis and system identification[J].IEEE Signal Processing Magazine,1991,8(3): 29-43.

[16]王志伟, 秦俊奇, 狄长春, 等.基于北斗差分定位的炮载惯导外场标定[J].中国惯性技术学报, 2016, 24(3):314-319.Wang Z W, Qin J Q, D C C, et al.Inertial navigation system’s field calibration based on Beidou-II differential positioning[J].Journal of Chinese Inertial Technology,2016, 24(3): 314-319.

The shaking error compensation for gun-board SINS

WANG Zhi-wei1, QIN Jun-qi1, YANG Gong-liu2, SHI Zhi-yong1, DI Chang-chun1, WANG Feng-jie3
(1.Ordnance engineering college, Shijiazhuang 050003, China;2.Beihang University, Beijing 100191, China; 3.Unit 63870 of PLA, Huayin 714200, China)

The gun-board strapdown inertial navigation system is taken as the research object.Because of the residual high order nonlinear error of the system can not be compensated effectively, a combination estimation method based on fast orthogonal search algorithm (FOS) is proposed, combined with Kalman filter (KF), which not only eliminates the linearity error, but also plays a good role in restraining the residual high-order nonlinear error of the system.The results show that, when GPS is outage, the navigation accuracy can be improved more effectively by FOS/KF compared with by KF-only.After the compensation, the average horizontal velocity error is only 0.034 m/s, the positioning error can be basically kept within 10 m, and the high precision autonomous navigation under nonlinear condition is realized.

self-propelled gun; nonlinear error; fast orthogonal search algorithm; SINS

V249.3

A

1005-6734(2017)05-0592-07

10.13695/j.cnki.12-1222/o3.2017.05.007

2017-05-20；

2017-08-28

国防预研基金（9140A09040112JB34111）

王志伟（1990—），男，博士，研究方向为惯性导航。E-mail: wzw505869351@126.com

联 系 人：秦俊奇（1961—），男，教授，博士生导师。E-mail: Qjq1961@yeah.net