两轮自平衡智能车直立行走研究

龚林强，杨萍，申涛，郑海霞，张淑珍

（兰州理工大学机电工程学院，甘肃兰州 730050）

两轮自平衡智能车直立行走研究

龚林强，杨萍，申涛，郑海霞，张淑珍

（兰州理工大学机电工程学院，甘肃兰州 730050）

两轮智能车直立行走及直立行走的稳定性一直是两轮自平衡智能车制作过程中的关键问题，针对建立的两轮自平衡智能车动力学模型，分析了两轮自平衡智能车自身无法维持直立状态的原因，并得出两轮自平衡智能车直立控制所需要的关键参数为智能车车身的姿态倾角，通过互补滤波将陀螺仪加速度计采集到的数据进行融合，得到准确的姿态倾角值，并以实验对比的方式得到了陀螺仪加速度计在两轮自平衡智能车上的最优安装位置，最终实现两轮自平衡智能车直立行走。

两轮自平衡智能车；平衡控制；陀螺仪；加速度计；安装位置

两轮自平衡智能车是一种轮式机器人，属于动态自平衡机器人的一种，是一种多变量、强耦合、参数不确定的二轮系统[1]，但其具有体积小、转弯半径为零、运动灵活等优点，所以近些年以来，二轮自平衡智能车的研究也成为了国内外研究的热点之一[2]。两轮自平衡智能车型属于倒立摆模型，在没有施加外力的情况下，智能车在前进过程中车身无法直立。

文中从首先从动力学的角度分析了两轮自平衡智能车自身无法直立的原因，以及两轮自平衡智能车直立控制中需要用到的关键参数，随后就陀螺仪加速度计安装位置的不同，对智能车自平衡控制造成的影响进行实验分析，最终而实现两轮自平衡智能车直立行走。

1 两轮自平衡智能车的动力学模型

1.1 倒立摆模型分析

本课题自主制作的两轮自平衡智能车如图1所示。

图1 智能车实体

文中以智能车车身与地面角夹角接近90°且能够平稳前进的状态作为智能车平衡状态，在运动状态下，将智能车力学模型简化为倒立摆模型，如图2（a）所示。

假设智能车向左运动，其质量为m，质心高度为L，加速度大小为a，由于惯性力F与重力G的存在，智能车车身会向右倾斜，车身受力如图2（a）所示，沿车身法线及切线方向对车身所受力进行分解，如图2（b）所示。

图2 智能车车身受力图

经过计算，图2（b）中各分力的大小如下式：

上式中，Fτ和Fn为惯性力沿智能车车身切线与法线方向的分力，Gτ和Gn为重力沿智能车车身切线与法线方向的分力，此时智能车受到的回复力为F1=mgsinθ+macosθ,方向与位移方向相反，导致智能车在无外力情况下无法自动恢复到平衡位置。

1.2 两轮平衡车系统动力学方程

根据对倒立摆的分析可得，为了使智能车能够在平衡位置稳定下来，必须施加一个与位移方向相同的外力T，假设外力T沿车身切线方向分力大小为:Tτ=mgsinθ+macosθ;当θ接近于0的时候，可近似认为：Tτ=m(g+k1)θ;其中k1=a/θ;此时，智能车能能够在偏离平衡位置处稳定下来。若Tτ＞F1，即k1θ＞a，k1＞a/θ，此时智能车车身切线方向所受合力的方向与位移方向相同，智能车车身在外力作用下可回到平衡位置。此外，增加阻尼力可以减少系统恢复至平衡状态所需时间，假设增加的阻尼力与车身偏离平衡位置的角度成正比，方向与Tτ所产生的加速度方向相同，上式可改写为：

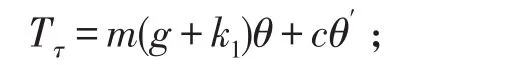
上式中，c为阻尼系数，为方便计算，另c=mk2，根据上式可得此时外力Tτ产生的加速度大小a1与角度之间的关系为：a1=kθ+k2θ′，其中k=g+k1，假设此时外力干扰引起智能车产生的角加速度为α(t)，根据Lagrange方程[3]建立智能车系统的运动微分方程：

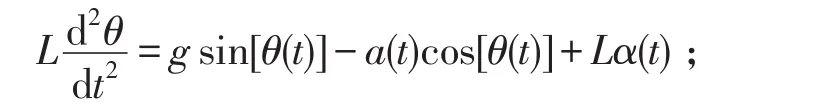
由于α(t)≠0，当θ趋近于 0的时候将公式α1=kθ+k2θ′代入系统运动微分方程，并化简可得：

此时，系统输入输出之间的传递函数为：

由此得出倒立摆模型不能自我恢复稳定的原因以及两轮平衡车维持平衡状态的条件为：

1）两轮自平衡智能车在没有外力作用的情况下，在偏离平衡位置处，受到的恢复力与运动方向相反；

2）两轮车要维持平衡状态，必须要测得精确的姿态倾角大小以及当前角加速度，将其作为反馈值并通过PI控制，输出相应的PWM方波作用于电机控制产生一个与加速度方向相同的外力，以此维持两轮自平衡车的动态平衡。

2 陀螺仪加速度计的安装位置对智能车平衡的影响

2.1 螺仪加速度计

为了测得准确智能车的姿态倾角与角加速度，必须在智能车上安装陀螺仪与加速度计，其中，但由于陀螺仪测得值是一个与角速度有关的瞬时量，需进行积分处理之后可以得到角度变化量，积分时间越短，输出角度越准确，但由于积分时间不可能无限小，故积分的误差会随着时间的推移而逐渐积累，导致测得的角度与实际角度不相符。而加速度计测量的是重力方向，其参考基准为竖直向下的重力，因此输出角度不会有误差，当智能车处于稳定匀速范围内前进的时候，加速度计的测量值在长时间内是准确的，但加速度计不能区分重力加速度与外力加速度，当智能车做变速运动时，它的输出角度与实际角度明显不相符。所以陀螺仪、加速度计当中的某一种是无法保证测量结果的准确性的，必须结合使用。

2.2 互补滤波

陀螺仪在低频段测量误差较大，而加速度计测量误差主要集中在高频段，在智能车直立方案中，选择将加速度计和陀螺仪测得的两种角度信号，通过互补滤波的方法进行融合，得到准确的角度信号，保证智能车的平衡性能，互补滤波原理图如图3所示。

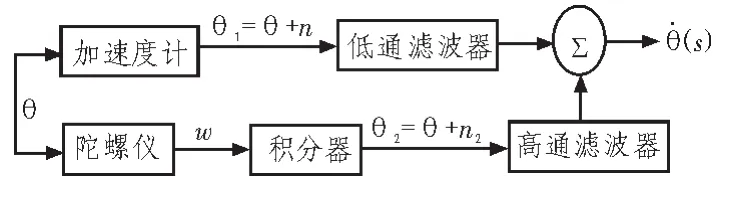
图3 互补滤波原理图

互补滤波程序如下：

上述程序中Acc_jiaodu为加速度计偏移角度，1 155为智能车处于平衡位置时刻，加速度计测得的角度；Gyr_jiaosudu为陀螺仪便宜角度，1 177为智能车处于平衡位置时刻，加速度计测得的角度；real_angle为通过互补滤波方法得到的实际偏移角度。

2.3 加速度计安装位置对智能车平衡性能的影响

为了验证陀螺仪加速度计安装位置的不同对滤波效果以及之后智能车直立平衡性能的影响，分别将陀螺仪加速度计沿着车身中轴线与地面成垂直角度的位置分别安装在智能车的3个不同位置进行单独测试并对比，如图4所示。

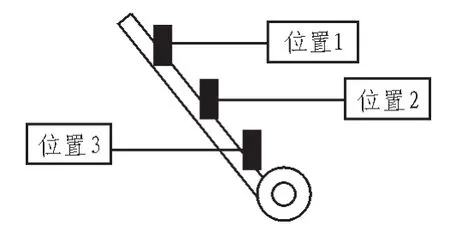
图4 陀螺仪加速度计位安装置选择示意图

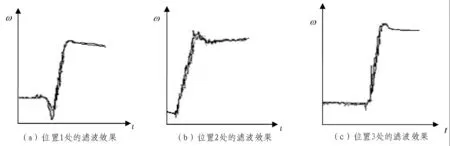
图5 不同位置陀螺仪滤波效果

如图5所示，其中纵轴表示互补滤波得出的拟合曲线的角度值，横轴代表时间变量，在调节PI参数确保滤波曲线跟随性一致的情况下，就陀螺仪加速度计分别处于图4所示3个位置时候测得的角度曲线以及智能车直立效果进行对比：

1）当陀螺仪加速度计处于图4所示位置1处时，滤波效果如图5（a）所示，智能车在回到平衡位置附近时加速度计得出的数据过冲很明显，智能车在恢复直立过程中再平衡位置两侧有较为剧烈的摆动；

2）当陀螺仪加速度计处于图4所示位置2处的时候，滤波效果如图5（b）所示，当智能车在回到平衡位置附近时，加速度计得出的角度曲线虽然过冲程度较位置1时有所减小，但智能车在平衡位置附近的摆动仍然比较严重；

3）当我们将陀螺仪位置选择在图4所示位置3的时候，让陀螺仪加速度计尽量与车轮转动轴平行，此时加速度计在智能车回到平衡位置附近时，得出的波形曲线的过冲问题有明显的减弱，如图5（c）所示；而在实际调试时候，智能车在平衡位置前后的摆动也大为减轻[4-17]。

3 两轮自平衡智能车直立行走控制

两轮自平衡智能车直立行走控制主要有以下3个部分：直立控制、速度控制、差速控制，直立控制可以保证智能车稳定在平衡位置处，程序设计如下：

上述程序中KP、KD为直立控制中的PD参数，real_angle为通过互补滤波方法得到的实际车身倾角，PWMOUT_Angle为输出值，用于电机转速控制。

另外，速度控制保证智能车能够稳定向前移动，差速控制能够保证智能车根据道路情况及时减速或转弯，智能车直立行走程序设计如下：

上述程序中，PWMOUT_Speed为设定的智能车前进速度，PWMOUT_Dir为根据智能车左右两侧传感器所测数据得出的差速值。

4 结束语

文中基于以MC9S12XS128处理器为核心的两轮自平衡智能车为研究对象，通过建立数学模型，得出了两轮自平衡智能车在没有外力的情况下无法维持直立行走的原因，再基于所建立动力学模型之上，通过理论计算的方法得出了智能车直立控制中需要用到的关键参数为智能车当前的姿态倾角。使用陀螺仪与加速度计测量智能车实际姿态倾角，通过互补滤波的方法对陀螺仪、加速度计测得数据进行融合从而得到智能车当前姿态倾角的精确值，最后通过实验对比的方法就陀螺仪与加速度计不同的安装位置对互补滤波效果以及智能车直立控制的效果进行分析，从而总结出陀螺仪加速度计的最优安装位置，最终实现了两轮自平衡智能车的直立行走。

[1]阮晓钢，孙荣毅.两轮自平衡机器人运动平衡控制研究[J].科学技术与工程，2014，14（24）:84-88.

[2]孟鹏，章 政.基于陀螺仪与加速度计的二轮自平衡控制系统设计[J].传感器与微系统，2014，33（10）:61-64.

[3]Guo Qi，Zhou Zhao-ying，Xiong Wei.Design of a barometricaltimeter based on a micro pressure sens-or[J].Nano Technologyand Precision Engineering，2012，10（4）:337-341.

[4]冯智勇，曾瀚，张力.基于陀螺仪及加速度计信号融合的姿态角度测量[J].西南师范大学学报：自然科学版，2011，36（4）:137-140.

[5]蒙祖祈，刘海刚，项华珍，等.小型两轮自平衡电动车系统的设计与研究[J].工业控制计算机，2015，28（3）:64-67.

[6]梁光胜，杜梦楠，周子豪，等.基于互补滤波的两轮自平衡车姿态控制[J].测控技术，2015，34（5）:72-74.

[7]卓晴，黄开胜，邵贝贝.学做智能车-挑战“飞思卡尔”杯[M].北京：北京航空航天出版社，2007.

[8]隋金雪，杨莉，张岩.“飞思卡尔”杯智能汽车设计与实现实例教程[M].北京：电子工业出版社，2014.

[9]李有堂.机械振动理论与应用[M].北京：科学出版社，2012.

[10]周牡丹，康恺，蔡普郎，等.两轮平衡车控制系统的设计与实现[J].自动化技术与应用，2014，33（10）:4-8.

[11]兰建军，李佳璐，刘颖，等.基于自适应互补滤波算法的轮式倒立摆控制[J].组合机床与自动化加工技术，2014，6（6）:66-68.

[12]张晓兵.独轮机器人姿态检测信息融合算法的研究[D].哈尔滨：哈尔滨工业大学，2015.

[13]SHEN Xiao-wei，YAO Min-li，JIA Wei-ming，et al.Adaptive complementary filter using fuzzy logic and si- multaneous perturbation stochastic approximation algorithm [J].Measurement，2012（45）:1257-1265.

[14]范竹青，张正华.轮式机器人直立控制研究及其实现[J].信息技术，2013（12）:141-144.

[15]张团善，李文真.单轮自平衡机器车的系统建模与最优控制[J].西安工程大学学报，2014，28（1）:77-83.

[16]梁华，李晓虹.杨光祥两轮自平衡机器人动力学模型分析及PID控制方法研究[J].重庆师范大学学报:自然科学版，2016（1）:163-167.

[17]高晓娟，徐光辉，张欢，等.基于加速度特征的人体跌倒检测算法[J].西安工程大学学报，2015，29（1）:90-94

[18]贾立，邵定国，沈飞天.现代控制理论[M].上海：上海大学出版社，2013.

Research on balance control of two⁃wheeled self⁃balancing vehicle

GONG Lin⁃qiang，YANG Ping，SHEN Tao，ZHENG Hai⁃xia，ZHANG Shu⁃zhen
（College of Mechano⁃Electronic Engineering，Lanzhou Univ.of Tech.，Lanzhou730050，China）

The perpendicularity and stability of the models’perpendicularity are main problems in the process of producing a two⁃wheeled self⁃balancing vehicle，based on the two self balancing intelligent vehicle dynamics model，we analyzed the reason for why two self balancing intelligent vehicle can’t maintain upright by itself，and we realized the key parameters for two self standing balance control is attitude angle，we get accurate attitude angle value by fusing the data collected by accelerometer in method of complementary filtering and obtained optimal installation position of the gyro accelerometer by the experimental comparison，finally we realized the upright walking of two⁃wheeled smart car.

two wheeled self balancing vehicle；balancing control；installation position of gyroscope and accelerometer

TP242.6

A

1674-6236（2017）22-0145-04

2016-09-13稿件编号：201609132

龚林强（1990—），男，甘肃岷县人，硕士研究生。研究方向:特殊环境下的机器人开发。