非线性负载条件下衡量功率畸变率的方法研究

亢梦婕，徐 晔，王金全，严豪杰，陈 凯

(解放军理工大学，江苏 南京 210007)

非线性负载条件下衡量功率畸变率的方法研究

亢梦婕，徐 晔，王金全，严豪杰，陈 凯

(解放军理工大学，江苏 南京210007)

对于含非线性负荷的独立微电网，负荷对系统的冲击导致功率发生严重畸变，如何反映冲击的大小，确定畸变功率是微电网发展中亟待解决的问题。针对含脉冲负载的独立直流微电网，忽略频率畸变的影响，对非正弦条件下的有功功率及其波动量进行推导，并对如何衡量功率波动的大小进行研究。依照相关标准搭建含柴油机-整流器-脉冲负载的微电网实验平台，测得系统运行时三相电压va、vb、vc及三相电流ia、ib、ic的变化曲线，基于AKAGIH的瞬时功率理论在时域中分析其有功功率，并采用Clark变换推导有功功率的功率波动量，定义功率波动率以衡量含脉冲负载独立直流微电网功率波动的大小，为提高电能质量、储能容量的配置提供新思路。

微电网；脉冲负载；瞬时功率理论；功率畸变率

0 引言

脉冲型功率负荷是一种典型的非线性负荷[1]。脉冲周期通常为几十或几百毫秒，当它作用于小容量微电网时，会引起输电线路中的功率大幅波动，致使电能质量降低，甚至一些敏感负荷无法正常工作[2]。平抑波动功率是削弱脉冲负载对微电网冲击性的关键，如何确定有功功率的波动量是研究的重点。

1983年AKAGI H针对非正弦电压且包含非线性负载的电力系统提出三相电路瞬时无功功率理论，此后经过不断的研究逐渐完善，突破了传统的以平均值为基础的功率定义，它包容了传统的无功功率理论，具有更广泛的适用范围[3]。

本文依照相关标准搭建柴油机-整流器-脉冲负载微电网实验平台，测得交流侧功率数据，并分析脉冲负载对微电网运行特性的影响。忽略交流频率畸变，基于AKAGI H的瞬时功率理论在时域上推导了含脉冲负载的电力系统，在非正弦条件下的三相有功功率及有功功率波动量，并定义功率偏差率，以反映实际功率畸变的程度。通过对实验系统进行测试，对比分析了系统不同运行模式下的功率偏差率，验证所提指标的合理性。

1 功率波动率的定义

脉冲负载条件下准确度量有功功率的畸变程度，对确定系统需要配置储能补偿的容量有实际的意义，一方面可以按需供给避免浪费，另一方面可以避免因储能配置不足而造成的系统运行不稳定[4]。为衡量交流侧单相功率的波动情况，本文从时域分析的角度定义功率波动率，定义如下：

(1)

式中：p(t)为交流侧单相瞬时功率；pr(t)为单相瞬时功率的参考功率；td为脉冲负载条件下单相电压的变换周期与脉冲负载周期的最小公倍数；ti为以td为差的等差数列，ti=ti-1+td；N为以td为周期的畸变功率波形的周期数。

在脉冲负载周期性作用下，交流侧功率的波动也呈周期性变化，并且任意时刻功率波动具有随机性，故采用标准差表示[5]。为了在时域范围内全面地反映出交流功率的波动情况，td的选取应兼顾交流电压的额定周期和脉冲负载的脉动周期，这样才能将交流功率在任意时刻的畸变情况考虑全面，因而本文td为脉冲负载工作周期与交流电压额定周期的最小公倍数。

pR为交流侧单相参考功率，为了能够准确反映功率波动的程度，参考功率pR的选取应尽可能还原出交流功率的实际输出特性[6]。本文不考虑频率畸变的影响，采用柴油机带与脉冲负载峰值功率相等的线性负载时交流侧的单相功率作为理想参考功率。

因此在某种峰值功率、占空比、周期的脉冲负载条件下，可以通过试验测得交流侧各相电压、电流，进而通过上述定义式计算出功率波动率δp、功率波动率δp反映功率整体波动情况，包括有功功率和无功功率两部分。如何在已知功率波动率δp的情况下确定储能需配置的容量，即有功功率的波动分量，是下一节主要讨论的问题。

2 波动功率的提取及补偿电流推导

在非正弦条件下进行电力系统分析，传统的功率理论已失效。本文基于AKAGI H的瞬时功率理论，采用Clark变换。在α-β坐标系下分析其有功功率，设三相电路各相电压、电流的瞬时值为：

(2)

(3)

式中：n表示谐波次数；Vn、In分别为三相电压、电流基波及第n次谐波的有效值，k=a,b,c；ω为角频率；φkn、δkn分别为电压、电流基波及第n次谐波的相角，k=a,b,c。将其变换αβ到坐标系：

(4)

其中，xa、xb、xc可以为三相电压或电流。将式(2)、(3)带入式(4)，可得vα、vβ及iα、iβ的表达式为：

(5)

(6)

功率可由下式计算：

(7)

p、q两个功率都具有一个恒定分量和一个振荡分量，由于瞬时功率可实现解耦控制，故本文单独考虑有功波动功率p的补偿。

P可以分解成两个分量的叠加：

(8)

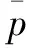
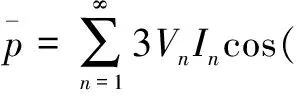
(9)

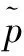
(10)

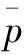
在待补偿功率采用负号的原因是为了强调补偿器将输出一个补偿电流，而补偿电流产生的功率与脉冲负载所吸收的不和需要的功率相反[7]。假设三相补偿电流的abc坐标系下的瞬时参考值ica、icb、icc，可通过从αβ坐标系到abc坐标系的反变换来计算，如下式所示：

(11)

(12)

由上述分析可知，在非线性负载条件下得到交流侧的电压、电流，可通过Clark变换计算出αβ坐标系下有功功率的波动量，进一步通过Clark反变换求得三相待补偿电流。

3 实验验证

在工程中经常采用柴油发电机组加整流器作为直流电源为移动型脉冲负荷供电。以发电机组中同步机与柴油机的功率比、整流器滤波电容值表示系统结构参数，以脉冲负载的峰值功率、开关周期、占空比表示脉冲负载的工作模式[8]。本文依照相关标准搭建了柴油机带脉冲负载的实验平台，如图1所示。实验系统由标称功率30 kW、额定功率36 kW、频率50 Hz的柴油机供电，通过整流器带脉冲负载工作。整流器滤波电容为4 000 μF，平波电抗为0.125 mH[9]。负载采用IGBT控制电阻通断模拟脉冲负载，脉冲负载周期为56 ms，峰值功率、占空比可根据实验进行调节。

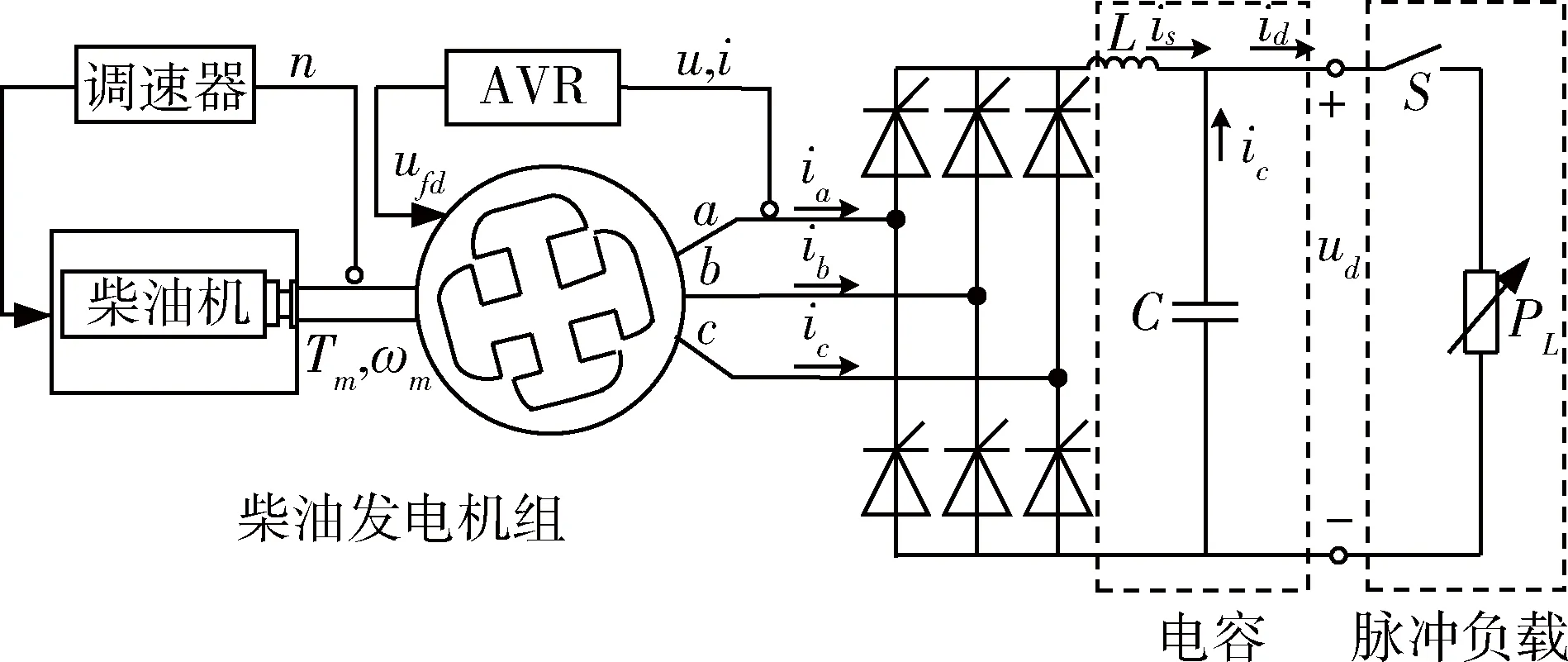
图1 柴油发电机组带脉冲负载实验平台

3.1δp随占空比变化关系

选择脉冲负载峰值功率30 kW、周期56 ms的脉冲负载，调整占空比从0.1变化到1，得到实验数据，计算出功率波动率如表1所示。

表1 改变占空比时DRV的变化

根据表1数据用SPSS软件可以建立起功率波动率随占空比变化的线性回归模型如下式所示：

δp=0.213 4+0.144 7D-0.079 4D2+0.047 6D3

(13)

根据上式拟合出δp随D变化的曲线如图2所示。可以看出，当脉冲型功率负载峰值功率、周期确定，仅改变其占空比时功率波动率δp随着占空比的增加而呈现线性递增的关系。

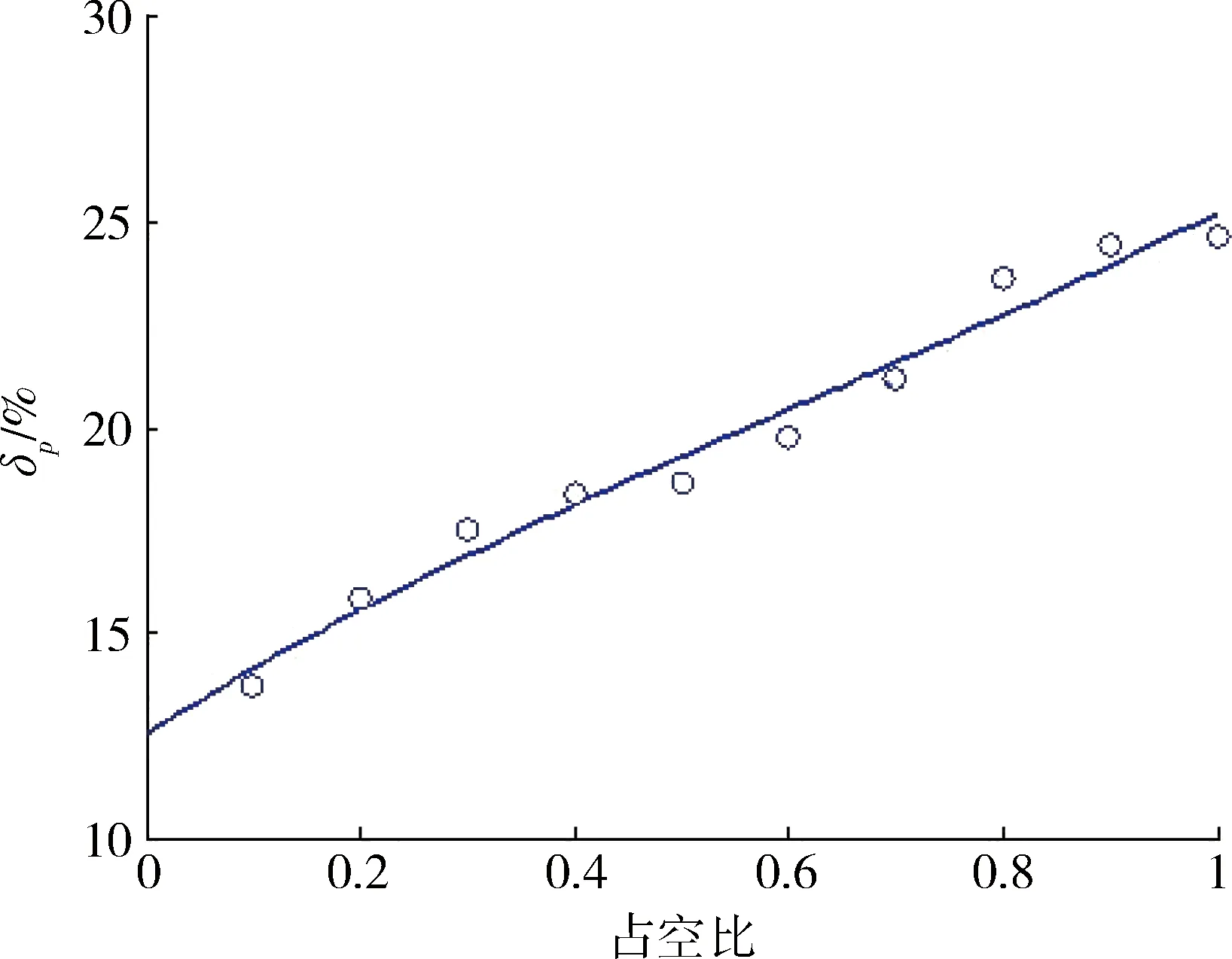
图2 功率波动率随占空比变化曲线

3.2δp随峰值功率变化关系

占空比为0.4时改变峰值功率，计算得δp如表2所示。

表2 δp随峰值功率PL的变化

根据表2用SPSS软件可建立起功率畸变率随峰值功率变化的线性回归模型如下式所示：

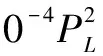
(14)

进而拟合出功率畸变率随峰值功率的变化曲线，如图3所示。

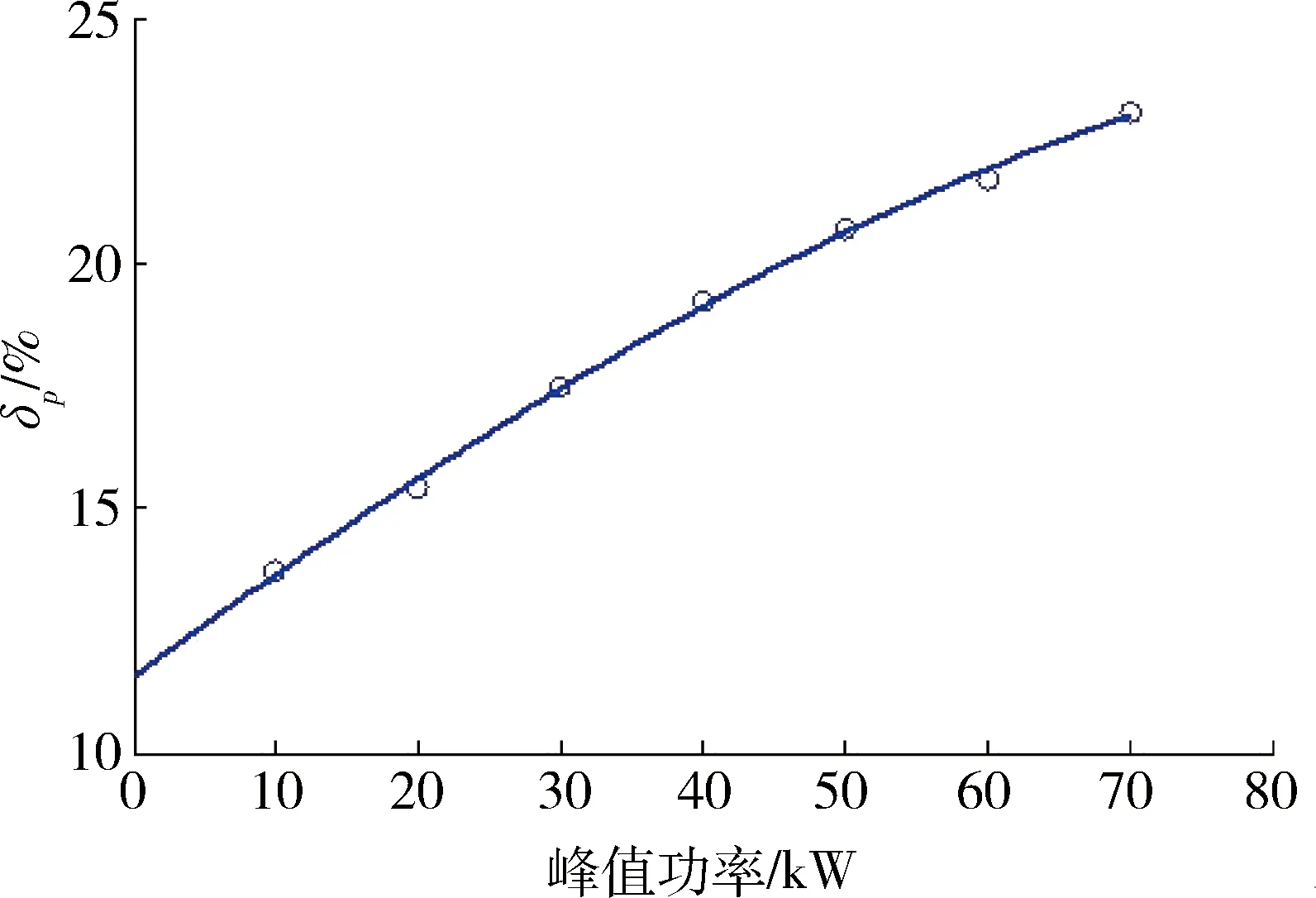
图3 功率波动率随峰值功率变化曲线

从图3可以看出，随着脉冲负载峰值功率的增大，交流侧功率波动率明显增大，这与实际情况相吻合。

4 结论

脉冲型功率负载的运行模式由工作周期、占空比、峰值功率三个参数决定，当微电网系统中含有脉冲型功率负载时，交流侧单相有功功率将发生大幅波动，改变脉冲负载的运行模式，将不同程度地引起有功功率波动。

本文首先依照相关标准搭建柴油机-整流器-脉冲负载微电网实验平台，测得交流侧功率数据。忽略交流频率畸变，基于AKAGI H的瞬时功率理论在时域上推导了含脉冲负载的电力系统在非正弦条件下的三相有功功率及有功功率波动量，并定义功率偏差率，以反映实际功率畸变的程度。通过改变脉冲负载占空比、峰值功率对实验系统进行测试，对比分析了系统不同运行模式下的功率偏差率，验证了所提方法的合理性。

[1] 胡亚超,徐晔,李建科,等.柴油发电机组-脉冲负载系统运行行为仿真[J].现代雷达, 2015,37(6):74-77.

[2] 鲁宗相,王彩霞,闵勇,等.微电网研究综述[J].电力系统自动化, 2007, 31(19): 100-108.

[3] AKAGI H,WATANABE E H,ARED M.瞬时功率理论及其在电力调节中的应用[M].徐政，译.北京：机械工业出版社, 2009.

[4] 赵广超,汤金华,黄继锋,等.小波分析在电力系统谐波治理中的应用[J].微型机与应用, 2011, 30(2): 109-111.

[5] 朱星阳,张建华,刘文霞,等.风电并网引起电网电压波动的评价方法及应用[J].电工技术学报, 2013, 28(5):88-98.

[6] 代仕勇, 彭晓涛,朱利鹏,等.基于负荷波动特性的联络线随机功率波动幅值估计[J].电力系统自动化,2013, 37(21):29-33.

[7] 姜卫东,吴志清,佘阳阳,等.电网不平衡时抑制有功功率二次波动的并网逆变器控制策略[J]. 电力系统自动化, 2014, 38(15):106-111.

[8] 陈静静，李建科，徐晔，等．柴油发电机组带非线性负载的实验研究[J]．现代雷达，2015，37(5)：84-87.

[9] 胡亚超．柴油发电机组-整流器-脉冲负载系统动态特性及功率匹配方法研究[D]．南京：解放军理工大学，2005.

2017-04-22)

亢梦婕(1993-)，女，硕士，主要研究方向：含脉冲负载的独立直流微电网混合储能容量配置。

徐晔(1964-)，女，硕士，硕士生导师，主要研究方向：新能源发电与智能微电网。

王金全(1964-)，男，博士，博士生导师，主要研究方向：新能源发电与智能微电网。

Study on the method of measuring power distortion rate under nonlinear load

Kang Mengjie, Xu Ye, Wang Jinquan, Yan Haojie, Chen Kai

(PLA University of Science and Technology, Nanjing 210007, China)

For the independent microgrid with non-linear load, the impact of the load on the system can cause serious damage to the power. How to reflect the size of the impact and determine the distortion of power is a problem to be solved quickly in the development of micro-grid. For the independent DC microgrid with pulse load, the frequency distortion is neglected, the active power and the fluctuation amount under non-sinusoidal condition are deduced, and the size of the power fluctuation is studied. The curves of the three-phase voltageva,vb,vcand the three-phase currentia,ib,icwere measured according to the relevant standard. The microgrid test platform was designed based on the AKAGIH’s instantaneous power theory in the time domain analysis of its active power, and Clark transform was used to derive the power of power fluctuations and define the power volatility to measure the pulse load independent DC microgrid power fluctuations in size. It provides new ideas for improving the power quality and energy storage capacity.

microgrid; pulsed load; instantaneous power theory; power distortion rate

TM912

A

10.19358/j.issn.1674- 7720.2017.22.027

亢梦婕，徐晔，王金全，等.非线性负载条件下衡量功率畸变率的方法研究J.微型机与应用，2017,36(22)：103-105，108.