必经点约束型最短路径问题的研究

王艳愉，李 强

(杭州电子科技大学 计算机学院，浙江 杭州310018)

必经点约束型最短路径问题的研究

王艳愉，李 强

(杭州电子科技大学 计算机学院，浙江 杭州310018)

为了解决网络路由中带有必经点约束的网络拓扑中最优路径的问题，提出了采用改进的蚁群算法和Dijkstra算法对最优路径进行规划。首先，针对含有必经点约束的问题，在信息素初始化时增加在必经点上的信息素。其次，为了能够更好地找到最优解，采用了狼群分配算法进行信息素更新，提高了收敛速度，并且采用了Dijkstra算法对蚂蚁找到的最优路径进行二次优化。最后，分别用不同节点和必经点规模的网络进行实验，并与基本的蚁群算法进行了比较，证明了改进蚁群算法的正确性和高效性。

最短路径；蚁群算法；必经点约束

0 引言

互联网技术和应用的不断发展，对当今网络通信流量的要求不断增大。流量大、速度快、费用低的传输方式是网络传输的关键。路径最短、代价最低的网络路由能够大大降低通信成本、节约网络资源，提高网络资源的利用率[1]。

最短路径问题是组合优化领域的经典问题之一，它广泛应用于计算机科学、交通工程、通信工程、系统工程、运筹学、信息论、控制理论等众多领域[2]。目前已有许多学者对最短路径问题进行了研究，但大多数传统的最短路径问题研究只考虑了起点和终点，并没有考虑有节点约束的网络，在实际应用中，如军事运输、物流运输等要考虑一些必须经过的点。例如在军事运输中，部队在执行任务过程中必须经过一些重要的战略地点，如加油站、军火库、桥梁等含有重要设施或资源的地点。因此研究含有必经点约束的网络最短路径问题有很重要的实际意义。

Dijkstra算法是经典的最短路径算法，虽然使用该算法找到的是全局最优的最短路径[3]，但在网络节点数量较大、网络边数较多时，存在内存占用大、时间复杂度高等不足[4]，并且Dijkstra算法不能很好地解决含必经点约束的最短路径问题。蚁群算法具有并行性、鲁棒性、正反馈性等特点[5]，已被广泛应用于求解组合优化问题，如著名的旅行商问题、车间任务调度问题、网络路由等许多复杂的组合优化问题[6]，但基本蚁群算法在求解路径规划问题时存在着容易陷入局部最优、迭代次数多、时间复杂度高等不足[7-8]。

本文提出了一种能够适用于在网络中求含有必经点约束的最短路径问题的蚁群算法信息素更新策略和状态转移策略，采用这种策略改进后的蚁群算法使得边上的信息素浓度能够不断朝着含必经点的最优路径去变化，收敛速度加快，更容易达到全局最优，与此同时，在用蚁群算法找出的最优路径上使用Dijkstra算法对路径进行二次优化，最后通过仿真实验验证了算法的有效性。

1 问题定义

定义有向图G=(V,E),其中V={v1,v2,…,vn}是顶点集，E={e1,e2,…,en}是边集，W={wij|i,j∈V}表示顶点i到顶点j的权重。对于给定的顶点o，d以及V的子集V′，寻找o到d的节点不重复的最短无环路径P，使得P经过V′中所有的顶点，并且o到d的路径的代价最小，即权重最小。

2 蚁群算法介绍

蚁群算法是由Dorigo、Maniezzo和Colorni等于1991年首先提出来的,它来源于蚂蚁寻食的行为。通过研究发现，蚂蚁个体之间是通过一种叫做信息素的外激素进行信息传递的。蚂蚁在行走过程中能感知周围信息素的强度，并朝着信息素浓度高的方向移动，当某只蚂蚁发现食物时，它在回巢的过程当中，会在返回的路上释放信息素作为标记，同伴发现后会沿着此路寻找到食物。当同伴中多只蚂蚁都发现了食物但路径长短不同时，因为蚂蚁在短的路径上往返所需要的时间相对较小，所以单位时间内走过的蚂蚁越来越多，在这条路径上的信息素浓度就会越强，因此，该路径上的蚂蚁就会越来越多，逐渐选出一条最优的道路，其原理如图1所示。

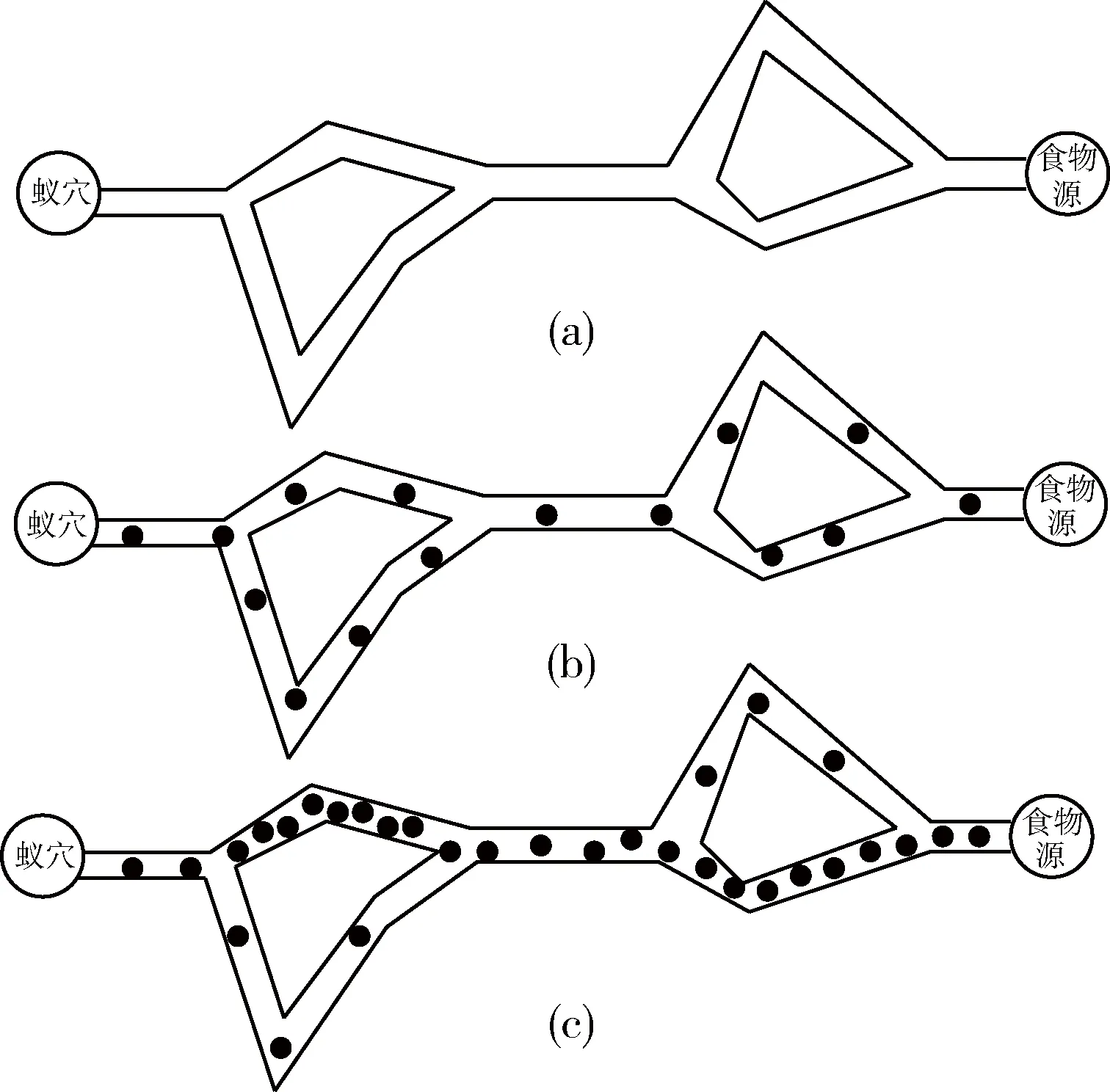
图1 蚂蚁寻找食物的过程

3 基本蚁群模型

(1)

其中novisited(k)表示蚂蚁从i位置到下一步可以选择的节点，应防止蚂蚁选择重复的节点。经过n个时刻，蚂蚁完成了一次循环，所有路径的信息素调整公式如下：

τij(t+n)=(1-ρ)τij(t)+ρΔτij

(2)

式中，(1-ρ)为信息素残留因子，ρ∈(0,1)。

(3)

公式(3)表示所有经过边(i,j)的蚂蚁留下的信息素。

(4)

式中，Q是信息素强度，为常量；Lk表示第k只蚂蚁在本次循环中走的路径总长度。

4 蚁群算法改进

为了使蚁群算法能够解决带有必经点约束的最短路径问题，针对基本蚁群算法的收敛性不足、容易陷入局部最优、搜索耗时严重等不足，需要对基本蚁群算法进行优化。

4.1改进蚁群算法的状态转移策略

由于蚁群算法是一种正反馈算法，这种正反馈机制可能使得在局部最优路径上的信息素浓度不断增大，随着迭代次数的增加，蚂蚁选择最优路径的概率逐渐降低，导致最后在最优路径上的信息素远低于局部最优路径上的信息素浓度，无法求出最优解。为此，本文对蚁群算法的状态转移策略进行了改进，引入了随机蚂蚁子群，并参与状态转移和信息素更新，从而扩大搜索解空间，使得算法得到最优解的概率更大。改进后的状态转移策略公式如下：

(5)

其中，r为随机子群，其蚂蚁数量为mr，p为信息子群，其蚂蚁数量为mp，mr约为mp的1/20左右，mr+mp=m，m为蚂蚁的总数。

在式(5)中，随机子群并不是完全随机地选择下一个点，而是根据启发因子进行状态转移，而信息子群则根据信息素浓度按照概率选择下一个点，从而使得蚁群算法的全局搜索能力得到了很好的提高。

4.2改进蚁群算法的信息更新策略

4.2.1狼群算法简介

狼群算法(Wolf Algorithm，WA)是2007年杨晨光等人根据狼群的捕食行为提出来的。狼群算法的主要思想是，狼群捕到猎物后，不是平均分配食物，而是先分配给最强壮的狼，再分配给其他弱小的狼。这样可以保证最强壮的狼不被饿死，能够继续捕获猎物，从而保证整个狼群不被饿死。

4.2.2基于狼群算法的信息素更新策略

传统的蚁群算法中，由于蚂蚁是根据路径上信息素的浓度进行路径选择，路径上既有好的蚂蚁留下的信息素，也有不好的蚂蚁留下的信息素，好的蚂蚁找到最优路径的概率更大，差的蚂蚁找到最优路径的概率则很低，因此差的蚂蚁留下的信息素会诱导后续其他蚂蚁向着错误的方向发展，从而导致陷入局部最优。

为此，本文采用狼群算法思想对信息素更新策略进行优化，即在每次循环结束后找出最好的蚂蚁和最差的蚂蚁，增大最好蚂蚁找到的路径上的信息素，去掉最差蚂蚁在路径上留下的信息素，其信息素更新公式如下：

(6)

(7)

(8)

式中，L*是本次循环中局部最优的路径长度，L**是本次循环中局部最差的路径长度，δ和ω分别为本次循环中局部最优和最差蚂蚁的个数。

5 改进蚁群算法的计算步骤

改进蚁群算法的主要计算步骤如下：

(1)蚁群初始化

确定蚁群规模m，初始化启发式信息参数α，β，每只蚂蚁的信息素为Q，最大迭代次数Nc，初始化每条路径上的初始信息素τij(0)=C以及信息素增量Δij(0)=0，初始化包含必经点的路径上的初始信息素为τxy(0)=D,(x,y∈K),K为必经点集，并且Dgt;C。

(2)将m只蚂蚁放到起点位置，并初始化m只蚂蚁的禁忌表tubai(i=1,2,…,m)以及novisitedi(i=1,2,…,m)，将起点添加到当前禁忌表tuba中，同时更新novisited表。

(3)路径构建

每只蚂蚁根据公式(5)选择下一节点，下一个节点的搜索范围限定在其当前节点的相邻节点矩阵内和蚂蚁个体的禁忌表tuba外，将所选路径节点添加到禁忌表tuba中，同时更新novisited表。

(4)局部更新信息量

对每只蚂蚁选择的路径(i,j)，根据公式(2)和(3)对路径(i,j)上的信息素进行局部更新，如果禁忌表tuba未满，则继续执行步骤(3)。

(5)信息素全局动态更新

当所有蚂蚁结束一次寻路后，在m只蚂蚁中找出到达终点并且包含所有必经点的局部最优蚂蚁和最差蚂蚁，按公式(6)进行信息素的全局动态更新。

(6)结束判断

判断是否符合结束条件，若符合则输出最优解，否则，转到搜索步骤重新搜索。

6 仿真实验

实验中网络拓扑图来自2016华为软件精英挑战赛。在网络中，起点和终点之间可能有多条有向边，但每条边的权重不同，因此采用编号来标记有向图中的每条边。

6.1算法正确性验证

为了方便描述、观察、验证该算法的正确性，本实验选择了网络节点规模较小的20个点的稀疏图进行试验。实验中，选择起始节点为2，终点为19，必经节点集为191014134。网络节点和边信息如图2所示,转化后的网络拓扑图如图3所示。

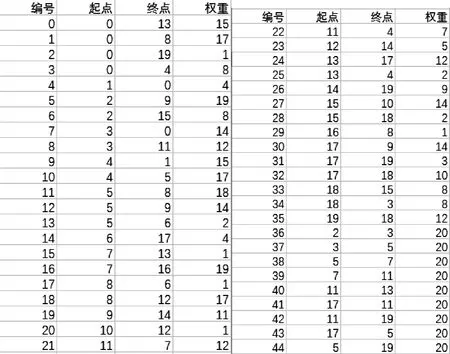
图2 网络信息图

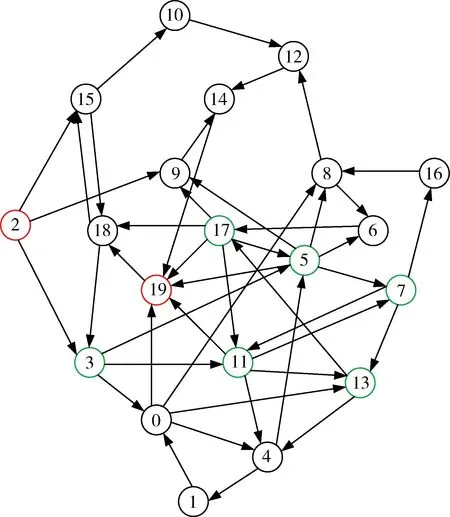
图3 网络拓扑图

改进蚁群算法的各参数的设置如下：Nc为2 000，m为50，α=6.0，β=1，ρ=0.8。通过改进的蚁群算法计算出经过上述必经点的最短路径为(用边的编号来表示)：6-gt;28-gt;34-gt;8-gt;21-gt;15-gt;25-gt;10-gt;13-gt;14-gt;31。

6.2试验在不同网络规模的时间效率

由于难以有效地对程序执行的空间效率进行监测，下面通过clock()函数来粗略记录算法的时间效率，分别对网络规模为20、300、600的情况进行多组测试计算执行时间平均值，必经点个数分别为1、5、10。实验结果如表1、表2、表3所示。

表1 20个节点执行时间表

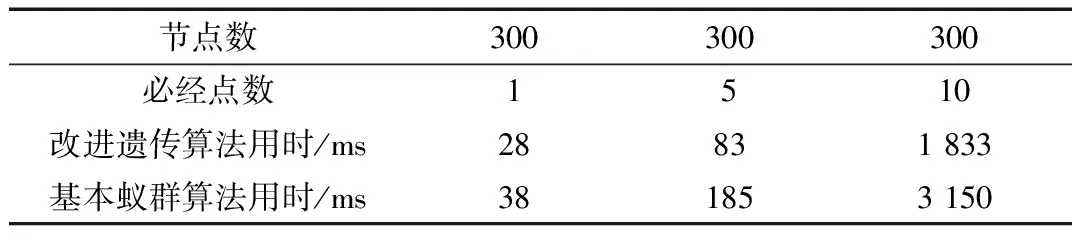
表2 300个节点执行时间表

表3 600个节点执行时间表

通过表1、表2、表3可以发现网络节点规模、必经点个数是影响求解效率的最主要因素。在必经点个数相同、网络节点规模较大时，执行时间显著增加；同样，在网络节点个数相同、必经点个数较多时，执行时间急剧上升。

7 结论

本文针对传统蚁群算法和Dijkstra在求解必经点约束型最短路径问题中的不足，采用狼群思想对信息素更新，同时增加了随机蚂蚁子群参与路径选择，防止蚂蚁陷入局部最优，并且在蚂蚁找出的最短路径上再用Dijkstra算法进行优化。通过实验证明了采用上述改进策略使得蚁群算法在求解必经点约束型最短路径问题上的正确性以及高效性，在实际运用中有重要意义。

[1] 王松. 基于蚁群优化多路径路由算法的研究与设计[D]. 济南：山东大学, 2016.

[2] 徐庆征, 柯熙政. 必经点最短路径问题模型及相应遗传算法研究[J]. 系统工程与电子技术, 2009, 31(2):459-462.

[3] 杨中秋, 张延华. 改进蚁群算法在交通系统最短路径问题的研究[J]. 现代电子技术, 2009, 32(8):76-78.

[4] 谭国真. 时变、随机网络最优路径算法及其应用研究[D]. 大连：大连理工大学, 2002.

[5] 周鹏, 张骏, 史忠科. 分段路径寻优算法研究及实现[J]. 计算机应用研究, 2005, 22(12):241-243.

[6] 葛延峰, 陈涛, 孔祥勇,等. 改进蚁群算法在城市汽车导航中的应用[J]. 控制工程, 2016, 23(1):133-137.

[7] 赵凯,李声晋,孙娟，等.改进蚁群算法在移动机器人路径规划中的研究[J].微型机与应用,2013,32(4):67-70.

[8] Liu Chang’an,Yan Xiaohu,Liu Chunyang,et al.The wolf colony algorithm and itsapplication[J]. Chinese Journal of Electronics, 2011,20(2):212-216.

2017-04-16)

王艳愉(1991-)，男，硕士研究生，主要研究方向：嵌入式系统、智能控制技术。

李强(1966-)，通信作者，男，博士，副教授，硕士生导师，主要研究方向：嵌入式智能控制理论、系统软件设计等。E-mail: hzlee@hdu.edu.cn。

Study of shortest path problem constrained by designated-points

Wang Yanyu, Li Qiang

(School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou China, 310018)

In order to solve the problem of optimal path in network topology with networked constraints, this paper proposes an improved ant colony algorithm and Dijkstra algorithm to plan the optimal path. Firstly, for the problem of containing the necessary constraints, the pheromone concentrations of the designated points is increased in the initialization of ant colony algorithm. Secondly, in order to find the optimal solution better, the wolves distribution algorithm is used to update the pheromone and improve the convergence rate. Also, the Dijkstra algorithm is used to optimize the optimal path of the ants. Finally, experiments were conducted with different scale of nodes and designated-points, and compared with the basic ant colony algorithm, it proved that the improved ant colony algorithm is correct and efficient.

shortest path; ant colony algorithm; designated-point constraint

TP18

A

10.19358/j.issn.1674- 7720.2017.22.008

王艳愉，李强.必经点约束型最短路径问题的研究J.微型机与应用，2017,36(22)：26-29.