基于磁纳米测温的弱磁信号检测系统

李 思，孙 毅，张国良

(郑州轻工业学院 计算机与通信工程学院，郑州 450000)

基于磁纳米测温的弱磁信号检测系统

李 思，孙 毅，张国良

(郑州轻工业学院 计算机与通信工程学院，郑州 450000)

肿瘤热疗是一种癌症治疗的新型手段，近年来，利用磁纳米粒子进行温度测量成为研究热点，利用其磁化信号可实现非侵入式温度测量.本系统由磁场探测装置、信号放大电路、数据采集系统和软件处理系统等4部分构成.首先，在研究分析的基础上，选用感应线圈式磁场探测装置，并在此基础上构建了等效电路模型，同时辅以差分线圈以剔除激励磁场信号的影响；其次通过对信号放大电路的仿真结果分析，发现采用级联的方式可以降低总噪声；然后用数据采集卡采集放大后的信号并通过数字相敏检波算法提取幅值；最后通过在LabVIEW平台开发的软件从软件层面进一步消除激励信号的影响，通过对实验数据的分析，很好的证明了系统的可靠性.

郎之万函数；磁纳米粒子；弱磁测量；数字相敏检波

伴随着医疗水平的进步，肿瘤的治疗手段也多种多样，但毒副作用相对来说也很大.目前采用的最主要的治疗手段仍然是手术、放疗以及化疗.寻求毒副作用小的治疗方法，或在现有治疗手段的基础上增加辅助方法，达到减小毒副作用的目的，为肿瘤患者提高治疗时的舒适度，提高治疗效果等，是目前肿瘤治疗急需解决的问题[1-2].近年来，临床热疗技术逐步发展，临床热疗也渐渐的被应用到了肿瘤的治疗上，且取得了良好的治疗效果，毒副作用相对也较小，已经引起了研究人员的高度重视.磁性纳米粒子在交变激励磁场下会发生温升效应，利用磁性纳米粒子作为热介导材料的新型肿瘤热疗方法，在动物实验中取得了显著效果.然而要使整个肿瘤组织温度达到42～43℃或者更高的同时，邻近组织低却于正常细胞的损伤温度，这就要求能够实时准确的掌控人体的内部温度.

1905年，科学家朗之万提出了经典的顺磁定律，实验证明，该顺磁定律能够很好的描述磁纳米粒子的顺磁性磁化曲线[3].在静态激励磁场H下，假设单位体积的磁纳米中有N个原子，其原子或分子的固有磁矩为，则其磁化强度M可表示为：

M=NμJL(α)

(1)

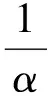
(2)

对其进行傅里叶展开，利用一次和三次谐波的五次展开项作为磁纳米粒子测温的数学关系模型.

(3)

在这一关系模型中，μJ、N、KB为已知量，磁纳米粒子温度T为未知量，因此只要知道其谐波幅值就可以得到温度信息.磁纳米粒子温度测量主要利用其磁化响应信号中的一次和三次谐波中包含的温度信息.然而，磁纳米粒子的磁化信号及其微弱，且淹没在较强的激励磁场信号和工频噪声中，所以要想从中检测出磁纳米粒子的磁化响应信号，且能够具有较高的信噪比，需要通过构建弱磁信号检测系统来实现[4].

1 弱信号检测系统

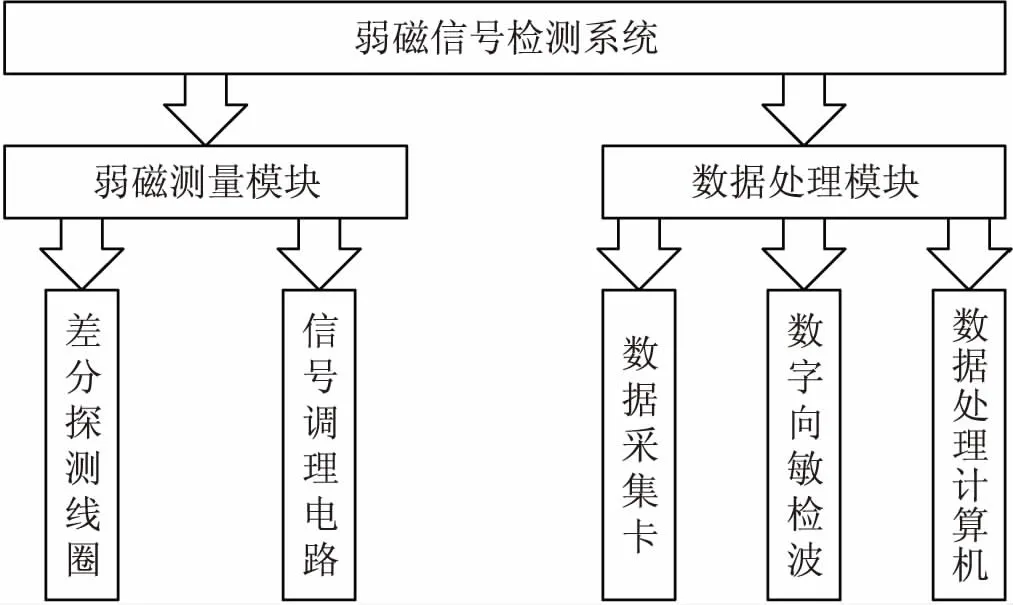
图1 弱磁信号检测系统总体框架Fig.1 Overall framework for weak magnetic signal detection system

本文设计的弱磁信号检测系统主要由磁传感器、信号放大电路、数据采集卡和数据处理计算机这几部分构成，系统总体框架如图1所示.

1.1感应线圈设计

本系统中采用的感应线圈为不带磁芯的空心线圈，其外部结构如图2所示.

图2 空心线圈结构Fig.2 Schematic diagram of the hollow coil structure

假设空心线圈的内径为d，外径为D，高为L，绕制匝数为N.以空心感应线圈几何中心点为原点建立三维坐标系，其Z轴为感应线圈的中心轴线，并将磁感应强度B在空心线圈几何中心点进行级数展开，BZ(0)为几何中心点的磁场，则：

(4)

(5)

其中：φ为总的磁通量，S1为横截面的面积，S2为剖面面积，V空心感应线圈的体积.

将式(4)带入到公式(5)中，由于空心感应线圈在结构上对称的原因，x、y、z奇次幂项可以正负抵消，即磁通量为零.空心感应线圈在进行信号测量时，其测量区域为电流为零的无源区域，因此满足方程：

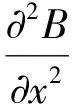
(6)

由于高于四次项比二次项小很多，可以忽略不计，则式(5)通过积分变换后得：

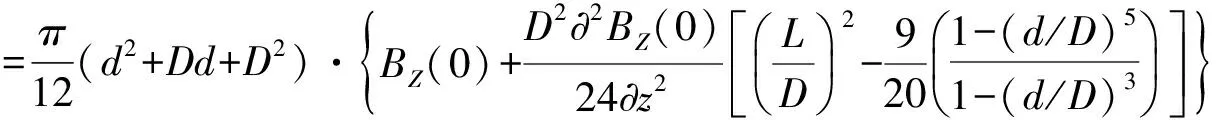
(7)

令上式右边第二项为零，即：

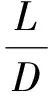
(8)

根据推导发现当空心感应线圈的几何尺寸满足式(8)时，空心感应线圈的总磁通量φ只与空心线圈所在的几何中心点处的磁场有关.为了获取最多信息，通常用初始灵敏度δ来表示.当空心线圈的匝数为N，被探测的磁场为H=H0sin(2πft)，f为磁场频率，H0为磁场强度，空心线圈横截面积为S时，获得的感应电动势可以表示为：

(9)

其中：μ0为真空磁导率初始灵敏度；δ为：

(10)

根据式(10)可知，初始灵敏度δ与N、S两个参数有关，因此提高空心感应线圈的初始灵敏度有两个途径，一是增加绕线匝数N，二是增加空心截面积S.但是由于空心感应线圈同样处于激励磁场中，在探测到磁纳米粒子的磁化信息的同时，也探测到了激励磁场信号，即剩磁.综合以上考虑，空心感应线圈的设计参数如表1所示.

表1 空心感应线圈参数

通过对磁纳米粒子磁化响应的COMSOL仿真发现，磁纳米粒子磁化后产生的磁场具有对称性，可以在以磁纳米粒子几何中心放置成对称的两个空心感应线圈，两个线圈的结构参数完全相同.具体示意图如图3所示.

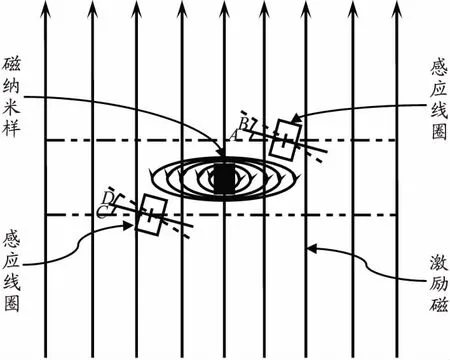
图3 磁场分布及感应线圈位置示意图Fig.3 Diagram of magnetic field distribution and induction coil location

当感应线圈1和感应线圈2在结构尺寸参数和绕制方向都相同，且摆放位置夹角与激励磁场夹角都相同的情况下，感应线圈1和感应线圈2中激励磁场信号的大小和方向也将相同.假设感应线圈1中心处激励磁场强度为H1、磁纳米粒子磁化强度为M1，感应线圈2中心处激励磁场强度为H2、磁纳米粒子磁化强度为M2，则可知两个感应线圈的输出信号为：

(11)

其中两个感应线圈中心激励磁场H1和H2可表示为：

(12)

式中：ω为激励磁场角频率，α1和α2表示相位，α1和α2可以具体表示为：

(13)

其中，R、L和C为感应线圈的阻抗特性.

此外，两个感应线圈中心磁纳米粒子磁场M1和M2可表示为：

(14)

将式(12)、(13)和(14)带入式(11)可得：

(15)

将两个空心感应线圈反向串联时，可得：

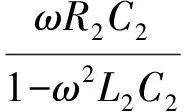
(16)

化简可得：

(17)

其中h(t)为激励磁场信号：

h(t)=Ksin(ωt+γ)

(18)

然而，当两个空心线圈的阻抗和位置不能够完全匹配时：

(19)

即激励磁场h(t)中，K≠0、γ≠0.使得无法完全消除激励磁场，因此，将在系统的软件设计中利用软件的方法来进一步消除激励磁场.

1.2信号放大电路

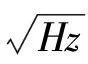
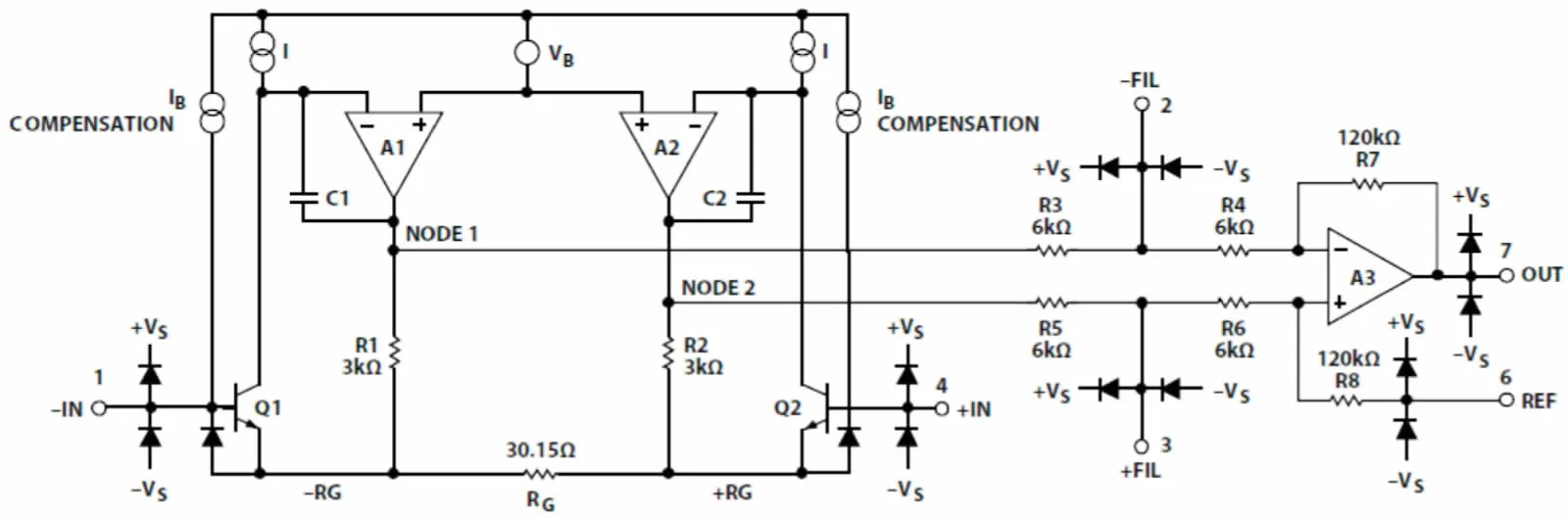
图4 AD8428内部简化原理图Fig.4 AD8428 internal simplified schematic diagram

为了有效的消除共模信号，其内部结构设计极为对称，这种对称不仅体现在结构上，更主要的是内部元器件性能上的严格统一.对于前级放大器，主要由A1和A2两个运算放大器分别构成两个电压同相放大器，其输出信号为正输入端的信号乘以增益系数，而增益系数由匹配电阻决定.两个同相放大器输出的电压信号全部施加到电阻RG上，其中差模信号将在RG上形成电势差，而共模信号由于电位相同，无法在RG上形成压差，从而无法产生电流[7].因此，差模信号将以200倍的增益通过前级放大器，而共模信号只能以单位增益通过，所以能够很好的抑制共模信号，其整体的传递函数为：

VOUT=2 000×(VIN+-VIN-)+VREF

(20)

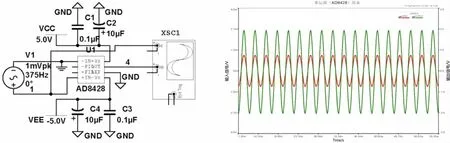
利用Multisim对其进行仿真，其仿真电路如图5所示，假设信号源为正弦信号，频率为375 Hz，幅度为1 mV.仿真结果如图6所示，利用示波器查看发现，幅度为1 mV的信号经AD8428放大后，幅度变为2，与其标定的放大增益符合.

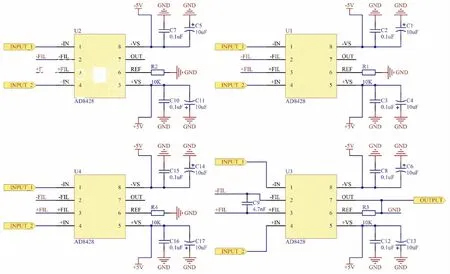
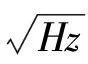
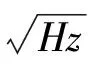
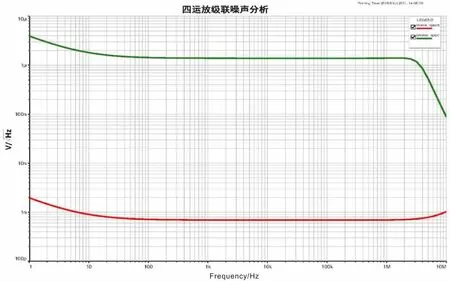
综上所述，使用四个AD8428组成级联放大电路，在不改变固定增益的前提下，且能将总噪声降低一半.

2 弱信号检测系统软件设计

2.1数据采集及保存

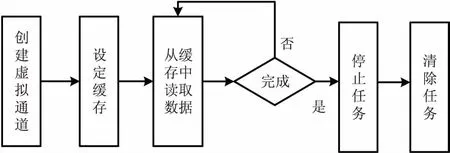
为了快速保存和读取大量数据，LabVIEW将数据以二进制的形式保存在特殊的文件格式中，称为TDMS文件.TDMS的逻辑结构分为三层：文件(File)、通道组(Channel Groups)和通道(Channels)，每一个层次上都可附加特定的属性(Properties)[8].能够灵活的对测试数据进行属性定义，也可根据属性对数据进行检索.如图11所示.

2.2数字相敏检波

数字相敏检波算法(DPSD) 常用于强干扰下的微弱信号检测[9]．相比其他方法而言，如自相关法、多重自相关法等，DPSD 算法拥有较高的检测精度，尤其是当信噪比低至－30 dB～ －60 dB 时，其优势更为明显．

假设待检测信号s(t)=Asin(ω0t+φ)，对s(t)在一个周期内进行傅里叶变换，并取ω=ω0.则有：

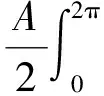
Aπsinφ-jAπcosφ

(21)

令R=Asinφ，I=Acosφ，得到：

S(jω0)=π(R-jI)

(22)

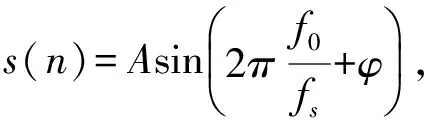
(23)

(24)

由式(22)、(23)和(24)可得：

(25)

(26)

经整理后可得：

(27)

φ=arctan(R/I)

(28)

图12 数字相敏检波算法原理框图Fig.12 Block diagram of digital phase sensitive detection algorithm

由此即可得到待检测信号的幅值以及相位信息，然而实际观测的到信号x(n)中除了包含有用信号s(n)，还包含加性噪声ω(n)，即x(n)=s(n)+ω(n)，由于ω(n)与sin(n)和cos(n)的弱相关性，用x(n)作为s(n)的估计值用上述方法进行检测，在信噪比较大时，测量误差很小，其基本原理框图如图12所示.

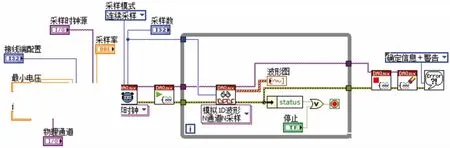
在本系统中，利用LabVIEW实现了该算法，其算法程序框图如图13所示.

2.3软件消除剩余磁场

图14 软件消除激励磁场原理框图Fig.14 Schematic diagram of software elimination excitation field

感应线圈在探测到磁纳米磁化响应信号的同时，也探测到了激励磁场的信号.从信号有用性上来说，此时的激励磁场信号属于噪声，并且远远大于磁纳米粒子的磁化响应信号，因此必须将其剔除.为此在硬件层面上，采用了两个感应线圈，通过对称摆放形成差分线圈对，将两个线圈的输出信号相减，去掉激励磁场信号，并且将磁纳米粒子的磁化响应信号变为原来的两倍，极大的提高了信噪比[10-11].鉴于对后续数据处理中温度反演精度的要求，在硬件层面上通过差分线圈对消除激励磁场的方法仍不能满足其要求，所以将在软件层面上进一步的剔除激励磁信号，提高信噪比，其原理如图14所示.感应线圈信号经前置放大后一路通过数据采集卡采集，在消除剩磁后提取出一次谐波幅值，另一路经过选频放大器后接入数据采集卡，消除剩余磁场后提取三次谐波幅值[12-13].由于剩磁信号也包含着谐波信息，因此还需利用并行谐波提取的方式来重构一个与剩磁信号完全相同的信号，这样可以得到一个只含有磁纳米粒子磁化响应谐波信息的信号[14].其并行提取流程如图15所示.

图15 并行谐波提取流程图Fig.15 Flow chart of parallel harmonic extraction

3 实验结果

以本文构建的微弱信号检测系统为平台，对磁纳米粒子在降温过程中的磁化响应信号进行采集，图16为利用热敏电阻测量的磁纳米粒子降温曲线，其温度从333 K下降到298 K，其实验结果如图17和图18所示.

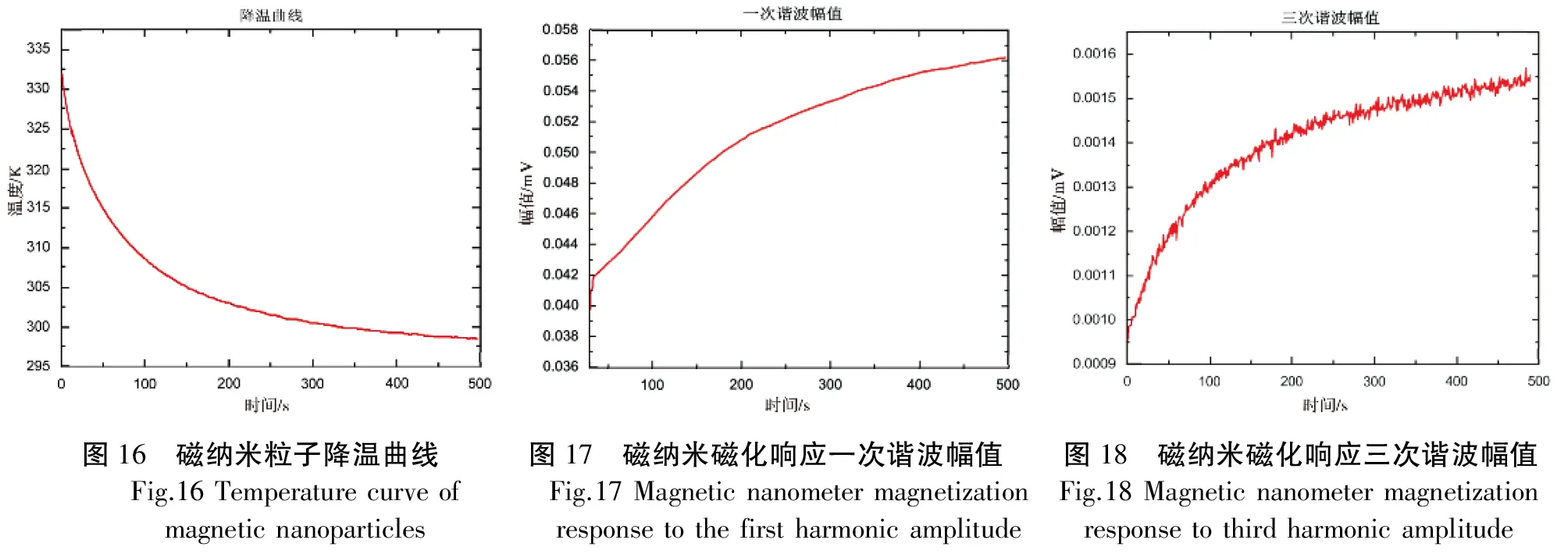
从其一次和三次谐波幅值随着磁纳米温度降低而发生变化，很好的验证了系统的准确性，并证实了磁纳米粒子的磁化强度与温度的相关性，为实现非侵入式温度测量打下了坚实基础.

4 总结

磁纳米粒子磁化响应的谐波信息中包含了温度信息.为了能够检测其磁化信息，进而反演温度，本文设计了一套基于磁纳米测温的弱信号检测系统，通过实验验证，该系统能够准确的测量磁纳米粒子的磁化响应信号.系统通过软件和硬件的协调完成了磁纳米粒子磁化响应信号的测量.通过实验数据分析，可以获得磁化强度和温度的关系，并能够很好的吻合理论模型，证明系统的精确性与稳定性.

[1] 陈万青,张思维,曾红梅.2015中国肿瘤登记年报[R].北京:军事医学科学出版社,2015.

[2] 尹晓玲.IL-12真核表达质粒构建及其瘤苗抗肺癌免疫作用研究[D].重庆:重庆医科大学,2009.

[3] 何梦华,沈朋.肿瘤热疗与肿瘤免疫在转化医学中的研究进展[J].基础医学与临床,2012,32(7):33-36.

[4] 张佳慧,秦丽娟.肿瘤热疗的研究进展[J].实用心脑肺血管病杂志,2012,20(9):1424-1426.

[5] PETER VAUPEL.Tumor micro environmental physiology and its implications for radiation oncology [J].Seminars in Radiation Oncology,2004,14(3):198-206.

[6] 张建纲.肿瘤热疗的历史和现状[J].肿瘤研究与临床,2003,15(5):50-53.

[7] 刘菡萏.磁性药物靶向递送的动力学研究[D].上海:上海交通大学,2008.

[8] LI Li,TIMO L M,TEN HAGEN,et al.Triggered content release from optimizedstealth thermosensitive liposomes using mild hyperthermia[J].Journal of Controlled Release,2010,143(2):274-279.

[9] JIM KLOSTERGAARD,CHARLES E SEENEY.Magnetic nanovectors for drug delivery[J].Maturitas,2012,73(1):33-44.

[10] MAHAM RAHIMI,ANIKET WADAJKAR,KHAUSHIK SUBRAMANIAN.In vitro evaluation ofnovel polymer-coated magnetic nanoparticles for controlled drug delivery[J].Nanomedicine:Nanotechnology,Biology,and Medicine,2010,6(5):672-680.

[11] SIMON C,VANBAREN P,EBBINI E S.Two-dimensional temperature estimation using diagnostic ultrasound[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,1998,45(4):1088-1099.

[12] RUDOLF S,PETER W A,DIETRICH H,et al.Temperam～monitoirng of interstitial the coagulation using MR phase images [J].JMRI,1997,8:188-196.

[13] 李扬,沈洪钧.软磁铁氧体磁心IEC标准和国内标准[J].磁性材料及器件,2015,46(3):73-77.

[14] 钟景.磁纳米温度测量理论与方法研究[D].武汉:华中科技大学,2014.

责任编辑：高山

WeakMagneticSignalDetectionSystemBasedonMagneticNanometerTemperatureMeasurement

LI Si,SUN Yi,ZHANG Guoliang

(College of Computer and Communication Engineering,Zhengzhou University of Light Industry,Zhengzhou 450000,China)

Hyperthermia is a new means for treating cancer,the method of temperature measurement based on magnetic nanoparticles has been a research hot spot in recent years.The temperature is measured using magnetic susceptibility of magnetic nanoparticles.The system is composed of four parts,namely,magnetic field detection device,signal amplification circuit,data acquisition system and software processing system.In this paper,the induction coil is used to detect the magnetic field,the equivalent circuit of the induction coil is constituted,and a differential coils is used to eliminate the residual magnetic field.By analyzing the simulation results of the signal amplification circuit,it is found that the cascade method can reduce the total noise.The signal is sampled by data acquisition card (PXIe-6368),extracted by digital phase-sensitive detection algorithms.The interference of residual magnetic field is eliminated in soft system,which is developed based on LabVIEW environment.The system is well validated through experimental data.

Langevin equation;magnetic nanoparticle;weak magnetic measurement;digital phase-sensitive detection

2017-03-15.

河南省科技攻关计划项目(162102410077);2016年度郑州轻工业学院研究生科技创新基金项目.

李思(1993-)，女(回族),硕士，主要从事智能信息处理的研究.

1008-8423(2017)04-0438-07

10.13501/j.cnki.42-1569/n.2017.12.019

TP273.5

A